自升式钻井平台桩靴踩脚印应对措施对比研究

杨 柳，贺林林, 2, 3，冯楚杰，刘旭菲

(1.重庆交通大学 河海学院，重庆 400074；2.重庆交通大学 国家内河航道整治工程技术研究中心，重庆 400074；3.重庆交通大学 水利水运工程教育部重点实验室，重庆 400074；4.浙江水利水电学院 水利与环境工程学院，浙江 杭州 310018)

随着对油气资源的大量需求，海上资源开发作业愈加频繁，自升式钻井平台在同一位置二次甚至是多次插桩作业的情况越来越多，这种工况通常被称为“踩脚印”。在桩靴踩脚印过程中，由于旧桩坑的存在可能导致自升式钻井平台插桩过程中桩靴两侧土体强度不均匀而发生偏移，严重时会导致桩腿弯曲变形，甚至平台整体滑移和扭转等，致使井位偏移，最终导致钻井平台倾覆、与邻近导管架平台相撞等事故的发生[1]，如图1所示。此类事故在实际工程中时有发生，墨西哥海湾某一桩靴直径为14 m的钻井平台[2]，在旧桩坑附近二次插桩时桩靴滑移进旧桩坑，造成平台结构损毁，经济损失惨重。近年来，在我国渤海海域自升式平台的踩脚印问题也越来越突出，如8号钻井平台在相同或相近井位作业时，曾多次发生平台倾斜和倾覆的事故[3]。且随着旧井位二次钻采需求的增多，由桩靴踩脚印导致海洋平台失稳事故比例也在逐渐增加。相关统计数据显示[4]，在过去十年左右时间内，因桩靴踩脚印造成的自升式钻井平台事故增长了4倍左右。例如在我国莺歌海区域的东方气田，由于开采次数比较密集，给后续平台在附近位置插桩就位带来了不可忽略的安全隐患[5]。因此，十分有必要对桩靴踩脚印工况下自升式钻井平台插桩稳定性及防治措施进行深入研究，以寻求减小自升式钻井平台插桩作业时滑移风险的方法。

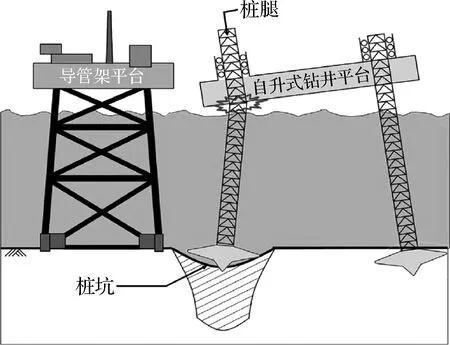
图1 平台和导管架平台相撞示意

针对桩靴踩脚印这一工程问题，学者们已开展了一定的研究，并提出了一系列的应对措施，包括：填平桩坑、试踩桩坑、优化桩靴结构型式(采用桶形与六孔莲蓬形桩靴等)、桩坑附近钻孔等[6]。填平桩坑法是指预先利用指定材料将旧桩坑填平的方法，研究表明填平材料的选取对填平效果的影响较大[7-8]。试踩桩坑法指预先踩踏旧桩坑使海床平整的方法，但由于难以预测试踩位置及深度，增加了该方法实际使用的难度[9]。Cassidy等[10]通过离心机试验研究表明，纺锤形和桶形桩靴基础均朝桩坑侧水平滑移，其中桶形桩靴的侧滑位移较纺锤形桩靴减小了27%，表明桩靴结构型式优化法对减小踩脚印工况不利响应效果较好。地基钻孔法指在地基土体中预钻一定数量空心孔洞，以减小桩靴踩脚印过程中桩坑对桩靴产生的不利响应。Hossain等[11]通过1g离心试验模型测试了地基钻孔法减小桩靴踩脚印工况不利响应的效果，证实了地基钻孔面积仅为桩靴面积9%时已能显著减小桩靴踩脚印工况不利响应，包括桩靴受到的水平力与弯矩值，然而在实际海床钻孔的可操作性未得到证实。

上述应对桩靴踩脚印工况的各类措施，虽然理论可行，但实际操作均存在一定的困难，且上述各种措施均需要附加机械设备，大幅增加了工程造价。为此，Jun等[12]与Hossain等[13]提出了桩靴结构型式优化措施，通过离心试验与数值模拟验证了新型桩靴减小二次插桩过程中结构滑移风险的有效性。文中基于前人研究成果，对桩靴的结构型式进一步优化，提出一种新型桩靴结构形式(六孔莲蓬形桩靴)如图2所示，且分析表明该新型结构型式能够较好地减少踩脚印过程中附加响应。可见，目前国内外已提出一系列可能减小自升式钻井平台插桩作业过程中工程风险的方法与措施，但对于上述各类措施的特点与差异，及其在应对踩脚印工况时的适用性及有效性研究，尚未见到公开发表的文献。

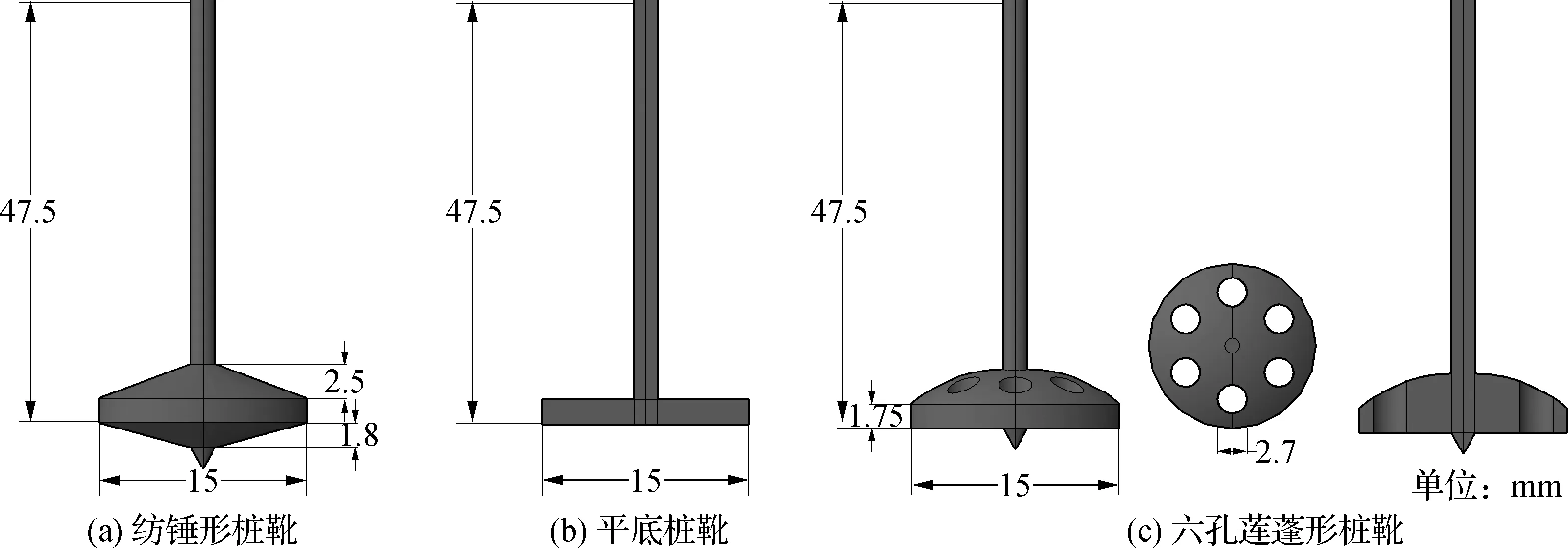
图2 3种桩靴结构示意

基于ABAQUS有限元分析平台，采用耦合欧拉拉格朗日(CEL)方法[14-17]建立桩靴土体相互作用的三维有限元模型开展相关研究。首先，借助CEL有限元数值分析方法定量分析了传统纺锤形与新型桩靴结构在不同插桩偏心距与不同桩坑深度时踩脚印工况下桩靴地基土体相互作用机制，明确了最不利桩靴踩脚印工况。且在此基础上，对比分析了新型六孔莲蓬形桩靴、试踩法与地基钻孔法3种桩靴踩脚印应对措施的适用性与有效性，可为应对自升式钻井平台桩靴踩脚印工况措施的选取提供参考。

1 有限元分析方法

1.1 有限元模型的建立

采用CEL大变形有限元方法建立了自升式钻井平台桩靴踩脚印工况的三维有限元数值计算模型，其中，将地基设置为欧拉体，桩靴设置为拉格朗日体，桩靴与土体的接触采用通用接触法则。切向方向，桩靴表面采用罚函数定义摩擦公式，摩擦系数取0.5[18-19]；法向方向设为“硬接触”，接触面之间能够传递的接触压力大小不设上限，当接触压力变为0或负值时，接触分离。

地基模型长度为8D(D为桩靴直径)、宽度为4D、深度为4D[20]，模型上方预留4 m深度的空单元。为了提高计算效率，计算模型取试验模型对应的原模型的一半进行建模分析，且地基土模型底部约束3个方向的平动自由度，四周约束法向平动自由度，桩靴模型仅允许法向移动。为了减小计算结果的振荡，地基网格采用结构化六面体单元EC3D8R进行剖分，桩靴采用线性减缩积分单元C3D8R划分网格且采用平底桩靴结构型式代替实际结构型式，如图2所示。桩靴及桩坑周围2.5D范围内土体网格采取局部加密，加密区网格最小尺寸为0.5 m[21]，加密区以外区域的网格越远越稀疏，网格划分如图3所示。CEL方法采用动态显示算法求解土体大变形过程，而自升式钻井船在插桩时是一个准静态过程，需要缓慢加载来实现。为了保证计算结果的准确性，计算中的桩靴贯入速率取0.5 m/s时，模拟的插桩过程可视为准静态过程[22]。因此，文中模型计算中桩靴贯入速率取0.5 m/s。

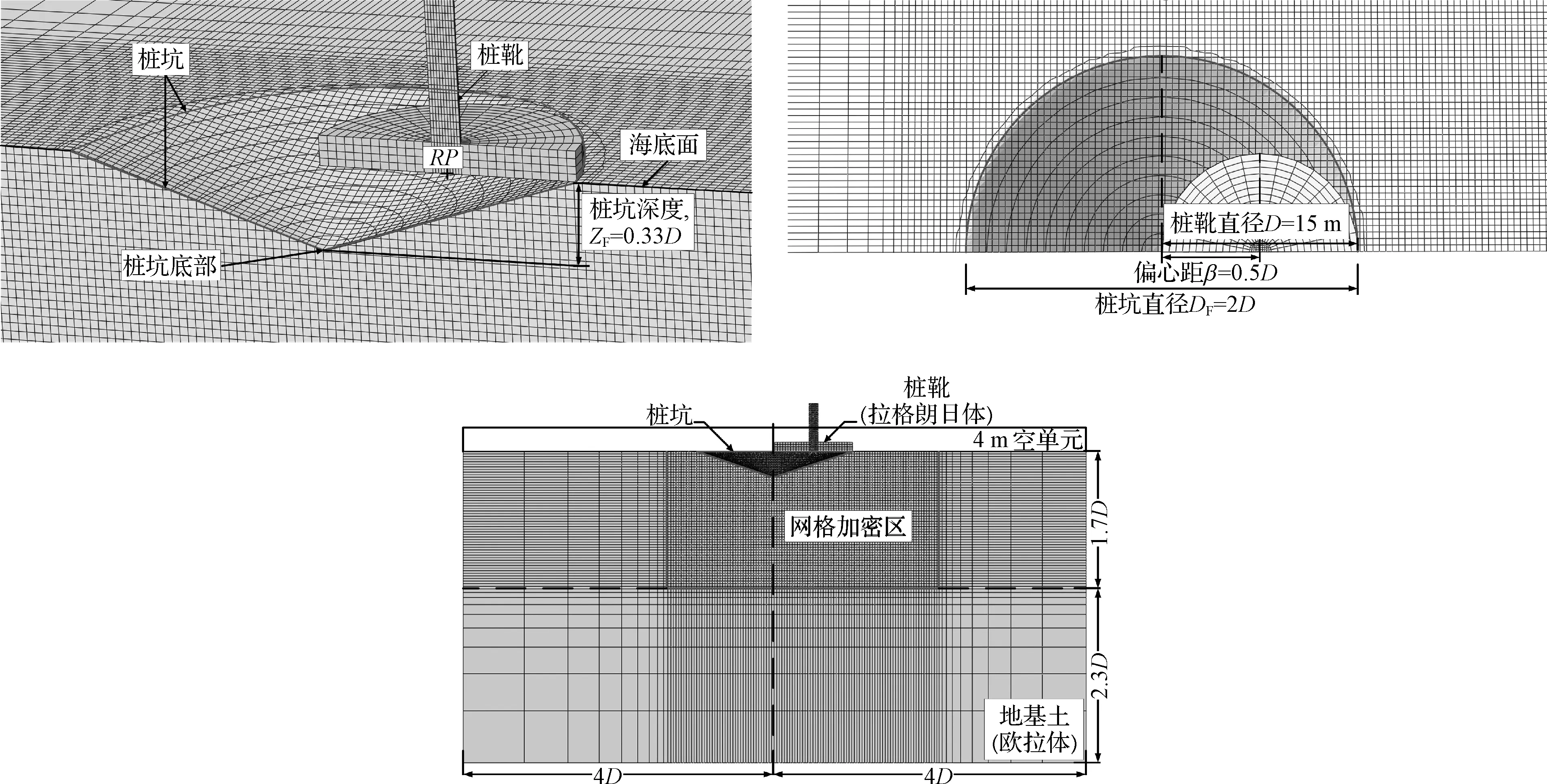
图3 桩靴踩脚印三维计算模型

1.2 有限元模型的验证

为了验证文中使用CEL方法的正确性，文中基于Kong等[23]离心试验数据建立了有限元模型，桩靴尺寸与地基土体材料参数，如表1所示。且基于该模型计算了插桩偏心距为0.5D的踩脚印工况下桩靴受力特性，并采用Kong等[23]离心试验结果、Jun等[24]与Zhong等[25]的数值模拟计算结果对文中有限元数值计算模型进行验证，如图4所示。

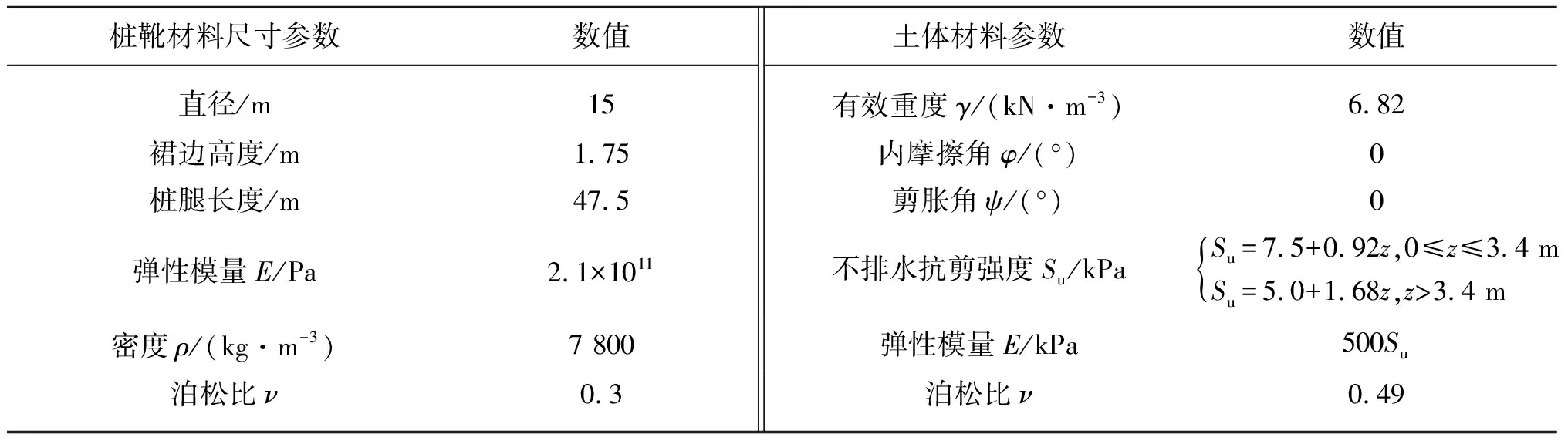
表1 桩靴尺寸与地基土体材料属性

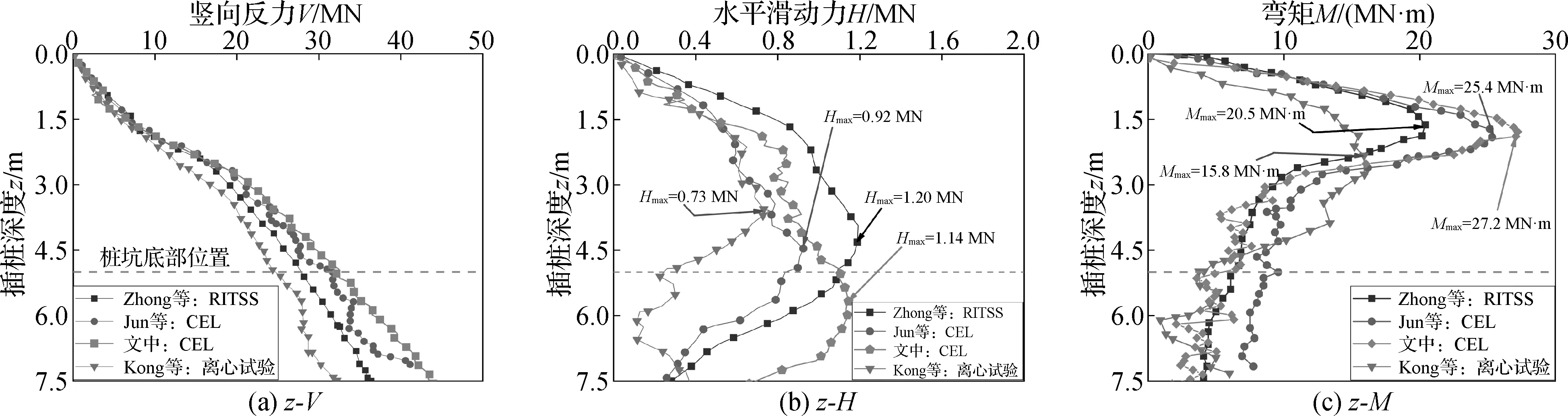
图4 CEL模型与离心试验桩靴所受内力对比

可见，文中数值模拟与离心试验所得计算结果变化趋势基本相似，但模型计算结果普遍偏大。究其原因是数值模拟土体的本构模型采用基于Tresca的理想弹塑性模型，而在离心试验中，由于土体存在一定软化特性，使得桩靴在贯入土体过程中土体更快地回填桩坑和回流，桩靴的水平力达到峰值后的速率降低相较于数值模型计算结果更快，但桩靴贯入一定深度后两者计算结果最终均会趋近于固定的值，整体吻合较好，进而验证了文中建立的CEL方法的正确性。

2 两种桩靴结构踩脚印工况承载特性对比分析

参考Kong等[23]在鼓式离心机中用切割刀片人工切出的3种理想倒圆锥形桩坑，其斜坡角度θ分别为9.5°、18.4°、33.7°，桩坑的深度在0.17D～0.67D(D为桩靴直径)之间，相关参数标注见图5。该形状的人造理想桩坑最大幅度降低了对周围土体的扰动程度，能够消除土体不均匀性带来的影响。

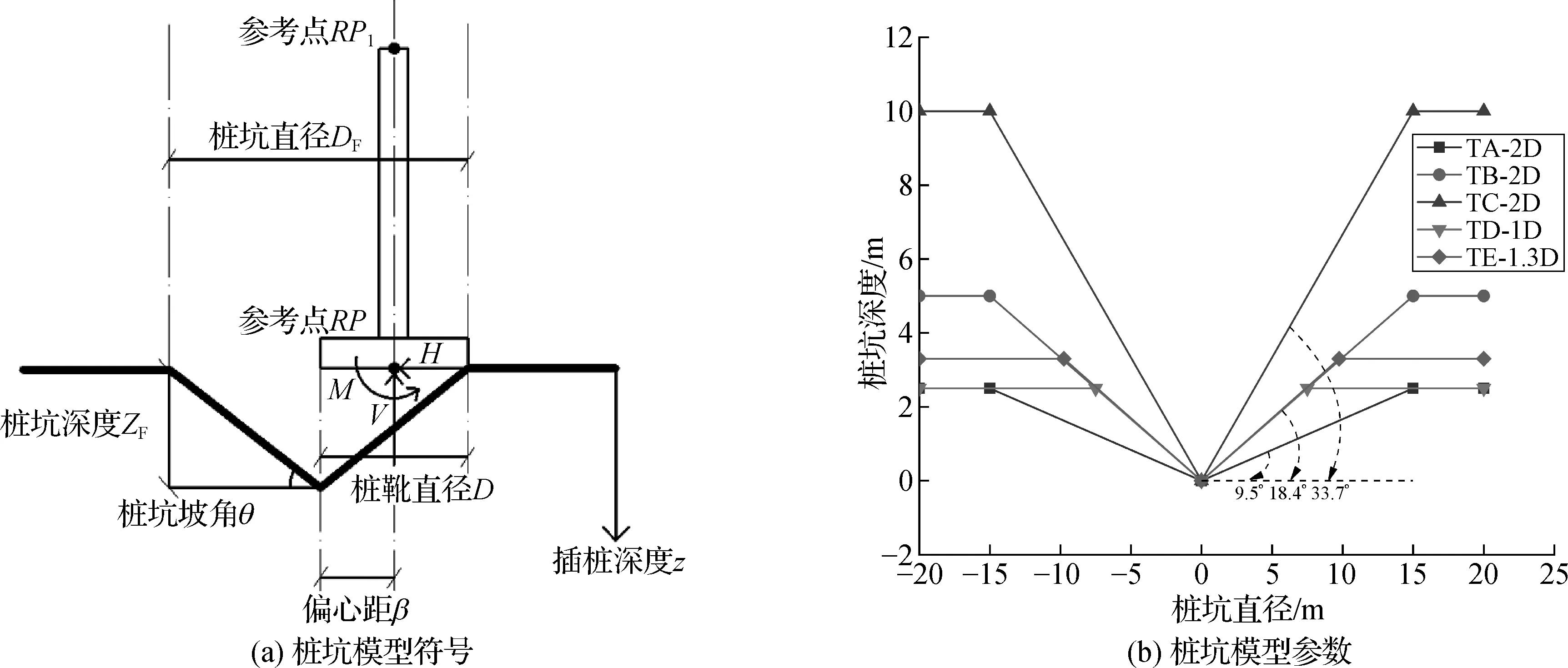
图5 桩坑模型符号及模型参数

图5所示桩靴踩脚印相关参数标注示意中，桩坑直径DF、桩坑深度ZF以及坡度和桩靴桩坑偏心距β等都有可能对桩靴踩脚印过程中桩靴的承载特性产生影响。RP为桩靴形心参考点，RP1为桩腿顶部参考点，代表桩靴、桩腿受力特性的特征点。为了分析这些参数的影响规律以明确最不利桩靴踩脚印工况，文中进行了一系列的分析，各工况参数设置如表2所示。各工况以AA-BB-CC-DD的格式进行编号，其中AA代表不同的桩靴结构(纺锤形桩靴SA和六孔莲蓬形桩靴SH2)；BB代表不同坡度的桩坑类型，TA、TB、TC类型桩坑的坡度θ分别为9.5°、18.4°、33.7°；CC表示桩坑直径，如2D即桩坑的直径为2倍桩靴直径；DD代表桩靴的插桩偏心距；例如，SA-TA-2D-0.25D指纺锤形桩靴在直径为2D的TA桩坑上以0.25D的偏心距插桩时的计算工况。

表2 数值计算工况总结

为了便于分析2种桩靴在TA、TB、TC桩坑中插桩偏心距工况不同时桩靴的承载特性差异，将3类桩坑的所有偏心距工况桩靴踩脚印过程中桩靴受到的水平滑动力Hmax、桩靴RP处弯矩Mmax、桩腿RP1处弯矩Mtmax、桩靴倾斜角αmax、桩腿偏移距δmax提取后进行对比分析，如图6所示。

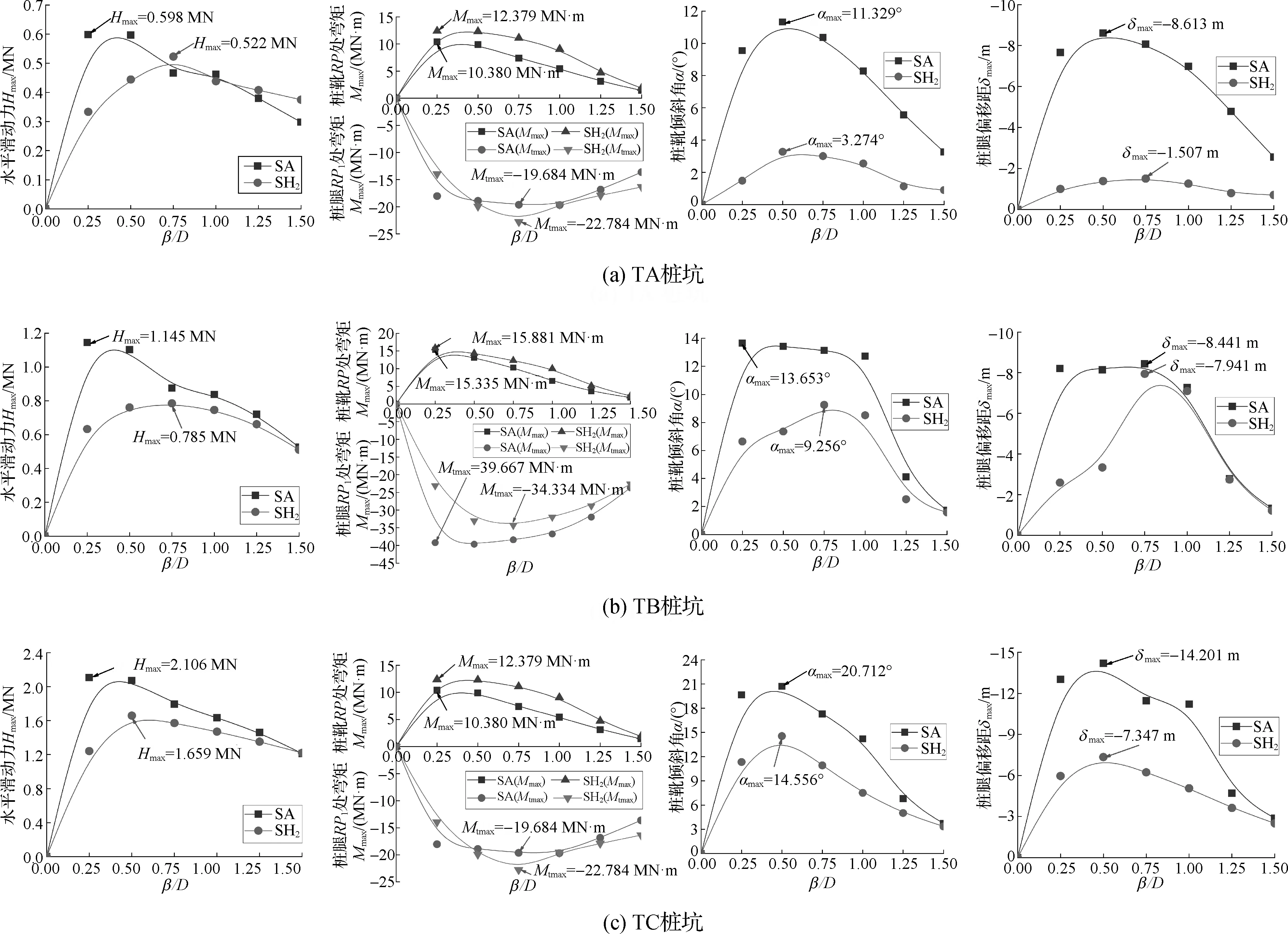
图6 两种桩靴不同偏心距不同桩坑Hmax、Mmax、Mtmax、αmax、δmax对比

可见，对于桩靴所受峰值水平滑动力Hmax，2种桩靴水平滑动力峰值的大小关系均为TC桩坑大于TB桩坑大于TA桩坑，且SH2型桩靴3种类型桩坑中不同偏心距水平滑动力峰值均小于SA型桩靴。对于峰值弯矩Mmax与Mtmax，两种桩靴桩腿RP1处峰值的大小均为TC桩坑大于TB桩坑大于TA桩坑，且SH2型桩靴贯入3种类型桩坑中，不同偏心距桩腿RP1处弯矩峰值均小于SA型桩靴。为了更直观地反映两种桩靴的桩靴与桩腿结构在不同偏心距插桩过程中受力的相对变化，绘制了基于VHM曲线的桩靴倾斜角αmax、桩腿偏移距δmax曲线。可以看出，SA桩靴倾斜角在偏心距为0.25D～0.50D工况时达到最大值，SH2桩靴的桩腿偏移距在偏心距为0.50D～0.75D达到最大值，两种桩靴αmax、δmax峰值的大小均为TC桩坑大于TB桩坑大于TA桩坑，且SH2桩靴的该值远小于SA桩靴。因此，可以得出，相对于传统纺锤形桩靴，六孔莲蓬形桩靴在抵抗踩脚印桩腿变形方面具有一定潜力，且当两类桩靴在插桩偏心距为0.50D且贯入TC桩坑时是桩靴踩脚印的最不利工况(SA/SH2-TC-2D-0.50D)。

3 3种应对措施对比研究

基于CEL法建立的自升式钻井平台桩靴踩脚印三维有限元数值计算模型，以SA-TC-2D-0.50D与SH2-TC-2D-0.50D工况下桩靴的承载特性曲线作为参照对象，对比分析了新型桩靴结构型式、试踩桩坑法与地基钻孔法对减小桩靴踩脚印不利附加响应的适用性和有效性。

3.1 试踩法

所谓“试踩”是指二次插桩前在旧桩坑危险距离以外进行预先踩踏，将周围土体挤入旧桩坑，或将旧桩坑附近土体压至同坑底相同深度，从而使海床平整而减小水平滑动力的产生。以偏心距0.50D作为插桩的最终位置，TC型桩坑作为研究对象，分别以中心距0.75D、1.00D、1.25D、1.50D、1.75D和2.00D进行试踩且试踩深度均设置为5 m，桩靴试踩后不同中心距工况下地基土体的变形模式与桩靴最终插桩位置如图7所示，模型参数的设置与前文一致。

图8为不同试踩中心距时，在不同深度处桩靴的承载特性特征曲线。从图8(a)竖向反力曲线可以看出，不同试踩中心距不会影响桩靴插桩的竖向反力，而六孔莲蓬形桩靴增大了结构的竖向承载能力。对于水平滑动力与桩靴RP1处弯矩曲线，不同中心距位置试踩工况曲线变化趋势相同。试踩中心距分别为0.75D、1.00D、1.25D、1.50D、1.75D时，桩靴受到的水平滑动力与桩腿顶部弯矩曲线均小于未试踩的SA-TC-2D-0.50D工况。其中，试踩中心距为1.00D、1.25D、1.50D时，桩靴的水平滑动力曲线与桩腿顶部弯矩曲线均小于SH2-TC-2D-0.50D工况，说明在该试踩中心距提前试踩，其减小踩脚印工况不利响应的效果大于采用六孔莲蓬形新型桩靴结构。对于综合考虑踩脚印工况桩靴受力相互作用与反映桩靴插桩稳定性的桩靴倾斜角与桩腿偏移距曲线，试踩中心距为1.00D、1.25D、1.50D时，其与SH2-TC-2D-0.50D工况下倾斜角与偏移距曲线的变化趋势均小于SA-TC-2D-0.50D工况，其中SA-1.25D工况曲线的变化趋势最小。

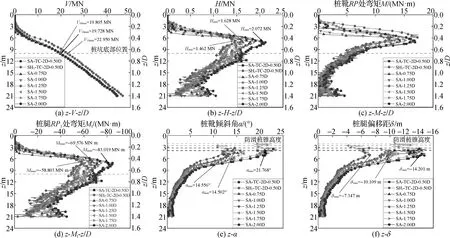
图8 不同试踩中心距工况下桩靴承载特性曲线

3.2 地基钻孔法

所谓“地基钻孔”是指人工在桩靴踩脚印贯入土体时沿桩靴周长在土体中预设一定数量空心孔洞，以减小桩靴踩脚印过程中桩坑对桩靴产生的不利响应。对于地基钻孔相关参数的设置，Hossain等[26-27]提出了一些建议：钻头直径与桩靴直径比值取0.047～0.065，或者钻孔有效直径与桩靴直径比值取0.059～0.094，桩靴周长内钻孔设置的面积占桩靴竖向最大投影面积为13%～60%。依据上述建议，文中采用地基钻孔法应对桩靴踩脚印工况的研究时相关参数的取值参考文献[26-27]。

同样地，将偏心距0.50D作为插桩的最终位置，TC型桩坑作为研究对象，以SA-TC-2D-0.50D、SH2-TC-2D-0.50D工况作为参照对象，借鉴Gao等[28]地基钻孔模型研究中设置的钻孔数量、直径以及钻孔深度对桩靴投影周长附近的地基土体进行钻孔处理，相关的工况设置如表3所示。模型中地基土体钻孔数量、钻孔布置以及桩靴投影周长与桩坑面积如图9所示，有限元其他模型参数的设置与前文模型一致且计算时取1/2对称模型。

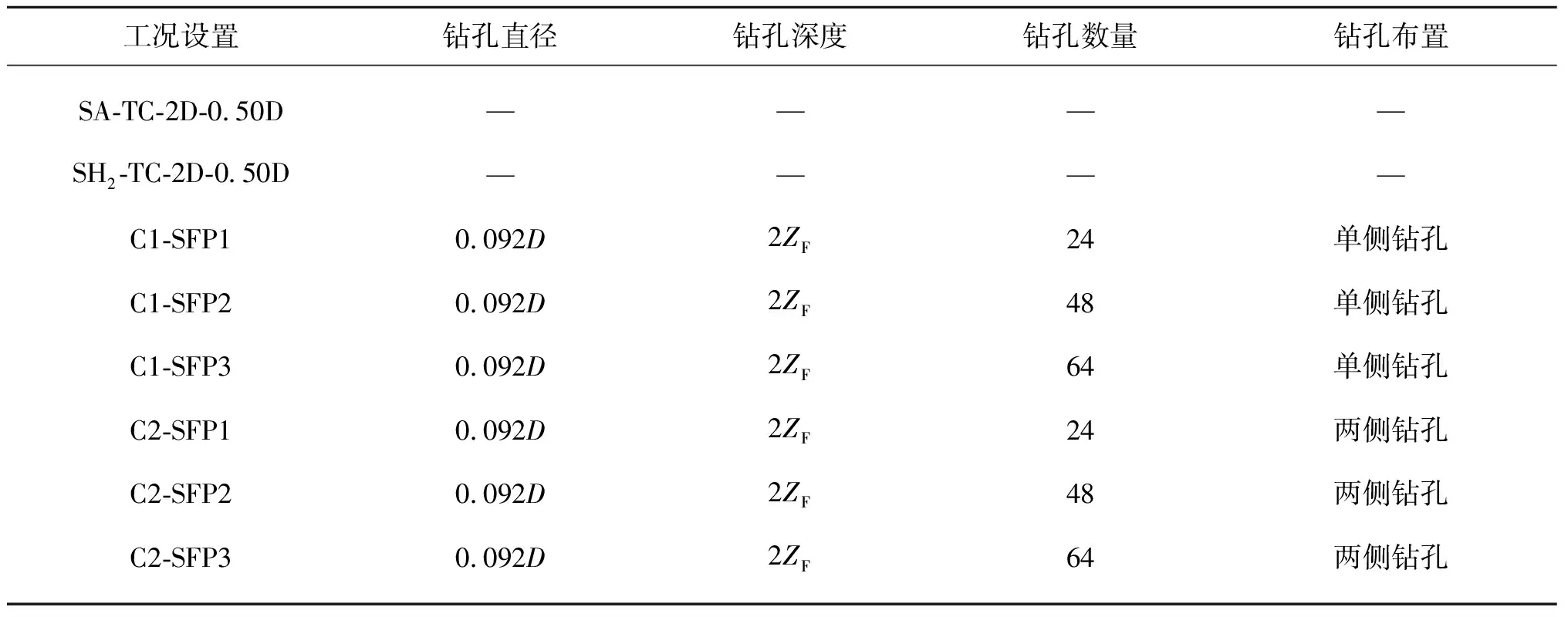
表3 地基钻孔工况设置

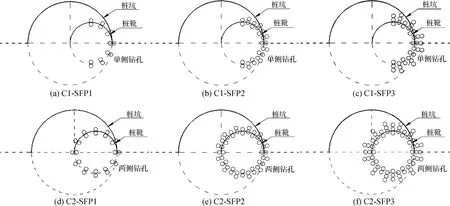
图9 桩靴地基钻孔工况示意

图10为不同钻孔工况下桩靴踩脚印后桩靴承载特性特征曲线。从图10(a)竖向反力曲线可以看出，钻孔数量越多，桩靴竖向投影面积下地基土体的强度越弱，桩靴受到的竖向反力越小。其中C1-SFP3、C2-SFP3工况下桩靴的水平滑动力曲线与桩腿顶部弯矩曲线均小于SH2-TC-2D-0.50D工况，证实了该法的有效性。若综合考虑踩脚印工况桩靴受力相互作用以及反映桩靴插桩稳定性的桩靴倾斜角与桩腿偏移距曲线，C1-SFP1、C2-SFP1地基钻孔工况下曲线的变化趋势与未试踩的SA-TC-2D-0.50D工况相似。而其他地基钻孔工况与SH2-TC-2D-0.50D工况下的倾斜角、偏移距曲线变化趋势相似，其中C1-SFP3工况下桩靴踩脚印后受到的附加应力最小，桩靴插桩稳定性最好。因此，证实了桩靴单侧64钻孔的C1-SFP3地基钻孔工况相较于六孔莲蓬形桩靴结构踩脚印有更好的桩靴插桩稳定性。

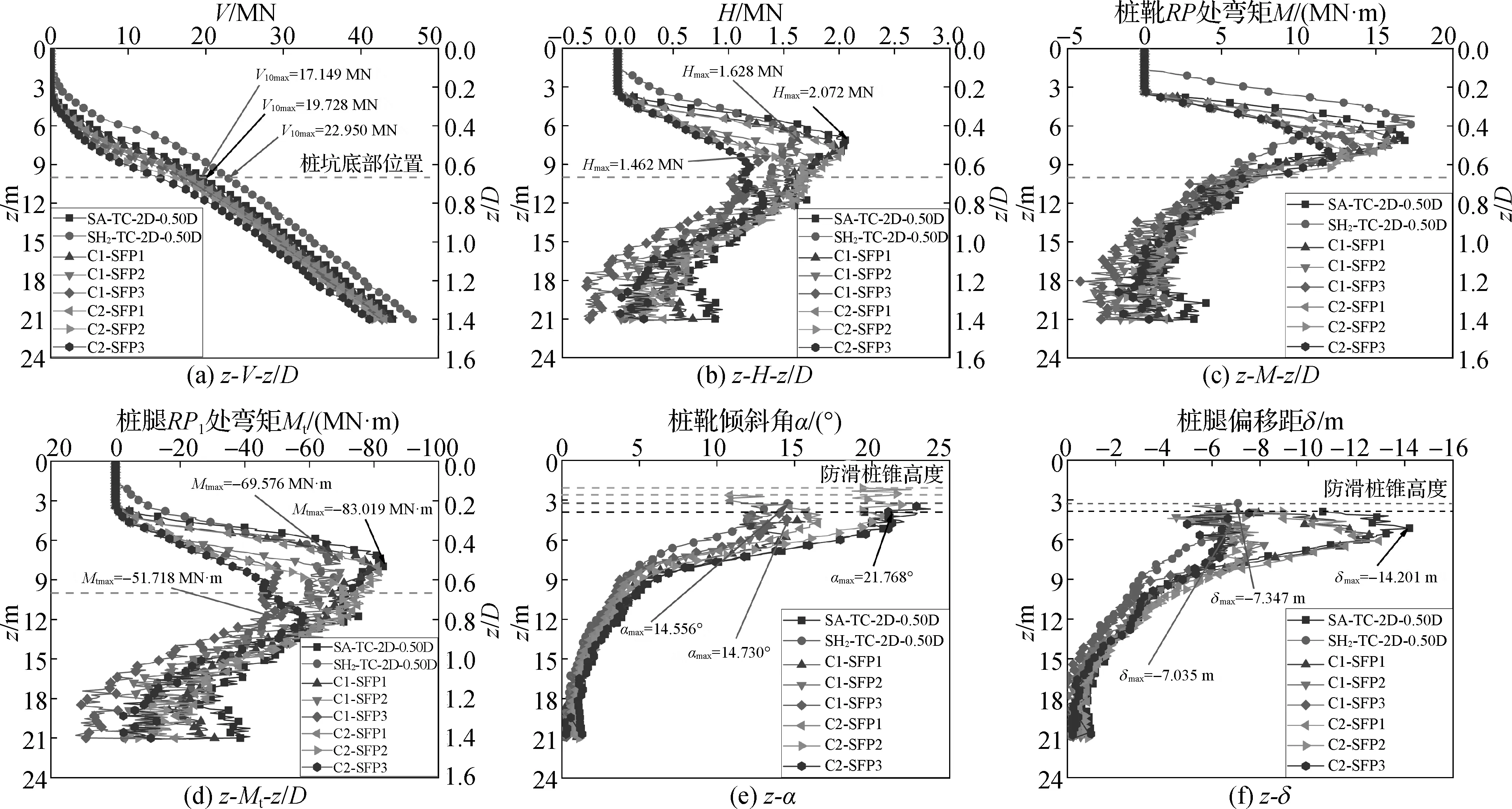
图10 不同钻孔工况下桩靴插桩承载特性曲线

3.3 3种方案应对桩靴踩脚印工况对比分析

为了更加直观地对比分析新型六孔莲蓬形桩靴、试踩法与地基钻孔法减小桩靴踩脚印后产生的附加响应效果，整理了3种方案应对桩靴踩脚印工况时Vmax、Hmax、Mtmax及反映桩靴插桩稳定性的αmax、δmax参数与参照工况SA-TC-2D-0.50D相关参数的对比，如表4所示。其中，中心距1.25D试踩工况桩靴受到的水平滑动力峰值与桩腿RP1处弯矩峰值相较于未试踩的参照工况降低了29.47%和29.17%。六孔莲蓬形桩靴反映桩靴插桩稳定性的倾斜角与桩腿偏移距参数相较于参照工况降低了33.13%和48.26%。而桩靴单侧64钻孔的C1-SFP3地基钻孔工况桩靴受到的水平滑动力峰值与桩腿RP1处弯矩峰值相较于参照工况降低了34.7%和37.7%，反映桩靴插桩稳定性的倾斜角与桩腿偏移距参数相较于参照工况降低了32.33%和50.46%。

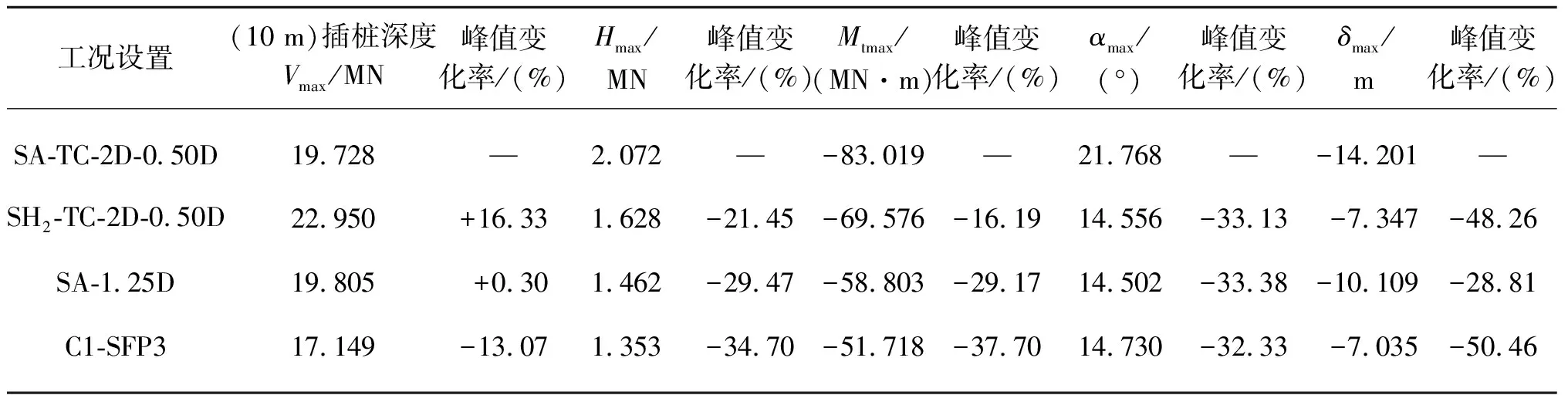
表4 3种方案应对桩靴踩脚印工况相关参数峰值及变化率

若考虑到桩靴插桩的竖向承载能力，六孔莲蓬形桩靴由于其结构的特殊性相较于纺锤形桩靴提高了16.33%的桩靴结构竖向承载能力，而地基钻孔法由于空心孔洞的存在减小了地基土体结构的连续性和强度使得桩靴结构的竖向承载能力降低了13.07%。

由此可见，3种方案均能有效降低桩靴踩脚印后产生的不利影响，提高桩靴结构的插桩稳定性。其中，依据减小桩靴附加应力的效果排序为地基钻孔法优于新型六孔莲蓬形桩靴优于试踩法。综合分析该3种应对桩靴踩脚印工况的措施可知，新型六孔莲蓬形桩靴结构虽理论上能较好地降低桩靴踩脚印后平台结构受到的附加响应，但该结构由于其桩孔的存在增加了结构受力复杂性的同时也提高了预制桩靴结构的难度；试踩方案在复杂的海洋地基条件以及淤泥覆盖等实际工况中，难以确定旧桩坑的位置和规模，则难以确定试踩位置以及深度，且试踩平台也存在一定失稳风险；而地基钻孔方案改变了土体的完整性减小了桩靴投影底部土体的承载能力，若要保证钻井平台结构的在位稳定性，则需增加平台桩结构的插桩深度或采用相关的地基加固措施，因此该方案会显著提高工程施工成本。可见，3种方案均存在优点与缺点，在选用相关方案应对桩靴踩脚印工况时需充分考虑相关施工环境条件与工程实际。

4 结 语

首先借助CEL有限元数值分析方法定量分析了传统纺锤形与新型桩靴结构在不同插桩偏心距与不同桩坑深度踩脚印工况下桩靴地基土体相互作用机制，明确了最不利桩靴踩脚印工况。在此基础上，对比分析了新型六孔莲蓬形桩靴、试踩法与地基钻孔法3种桩靴踩脚印应对措施的适用性与有效性。得到以下结论：

1)相对于传统纺锤形桩靴，六孔莲蓬形桩靴的倾斜角与桩腿偏移距参数降低了33.13%和48.26%，证实了六孔莲蓬形桩靴在抵抗踩脚印桩腿破坏方面具有一定潜力，且当两种桩靴在插桩偏心距为0.50D时贯入TC桩坑的过程为桩靴踩脚印的最不利工况。

2)相同土体参数条件下，采用中心距为0.75D、1.00D、1.25D、1.50D、1.75D试踩方法均能降低桩靴踩脚印工况下桩靴受到的附加应力，提高桩靴插桩稳定性。其中中心距1.25D试踩工况桩靴受到的水平滑动力峰值与桩腿RP1处弯矩峰值相较于未试踩纺锤形桩靴工况降低了29.47%和29.17%。

3)相同土体参数条件下，采用C1-SFP2、C1-SFP3与C2-SFP2、C2-SFP3工况地基钻孔方案均可较大幅度降低桩靴踩脚印工况下桩靴受到的附加应力，提高桩靴插桩稳定性。其中桩靴单侧64钻孔的C1-SFP3地基钻孔工况桩靴受到的水平滑动力峰值与桩腿RP1处弯矩峰值相较于参照工况降低了34.7%和37.7%。

4)3种方案均能有效降低桩靴踩脚印后产生的不利影响，提高桩靴插桩稳定性。以最终桩靴贯入产生的不利附加响应作为上述方法功效优劣评定标准进行比较：地基钻孔法优于新型六孔莲蓬形桩靴优于试踩法。