软刚臂单点系泊系统静力特性分析

李 鹏，孙丽萍, 2，马 刚, 2, 3，马荣太，王宏伟, 2

(1.哈尔滨工程大学 船舶工程学院，黑龙江 哈尔滨 150001; 2.工业和信息化部深海工程装备与技术重点试验室，黑龙江 哈尔滨 150001; 3.哈尔滨工程大学烟台研究院，山东 烟台 265501; 4.中海油研究总院有限责任公司，北京 100028)

单点系泊(single point mooring，简称SPM)指允许船舶随着盛行风和海况的变化，围绕着单个系泊点自由回转，从而处于风、浪、流合阻力最小位置的系泊方式。与多点系泊方式相比，单点系泊的显著特点是“点”系泊，船体像风向标一样转动，即风向标效应，大幅减小了风力和海流力对船体运动的影响。其中，软刚臂系泊系统是众多单点系泊形式的一种[1]。

软刚臂起源于单锚腿系泊系统，单锚腿系泊系统的主要构件是一个大浮筒，它漂浮在海面上，下端连接海底，上端则与船体相连。后来浮筒演化成一个柱状的浮力舱直接固定在海底，缩小了船体运动半径，也避免了浮筒随着海面升沉对自身和其他相关设备造成破坏。经过进一步发展，连系着船体的绳索逐渐演化成为刚臂(刚性桁架)，这种刚臂使船体和浮筒保持了恒定的距离，避免了碰撞；同时，也避免了绳索突然被拉直时的巨大冲击力。

经过不断完善过后，简单的刚臂形式演化成为现在的柔性多体结构，其由系泊腿(主要采用锚链)和刚臂(刚性轭架)组成，并通过单轴铰或双轴铰连接在一起。与单纯的刚臂形式相比，船体向单点塔方向运动时，这种多体结构允许船体有更多的相对运动，减小了刚臂与船体的直接作用，增加了缓冲。因此，相对刚臂系泊，这种刚柔多体结构形式叫做软刚臂系泊，软刚臂系泊系统的示意如图1所示。以软刚臂是否处于水中分为水下软刚臂[2]和水上软刚臂。

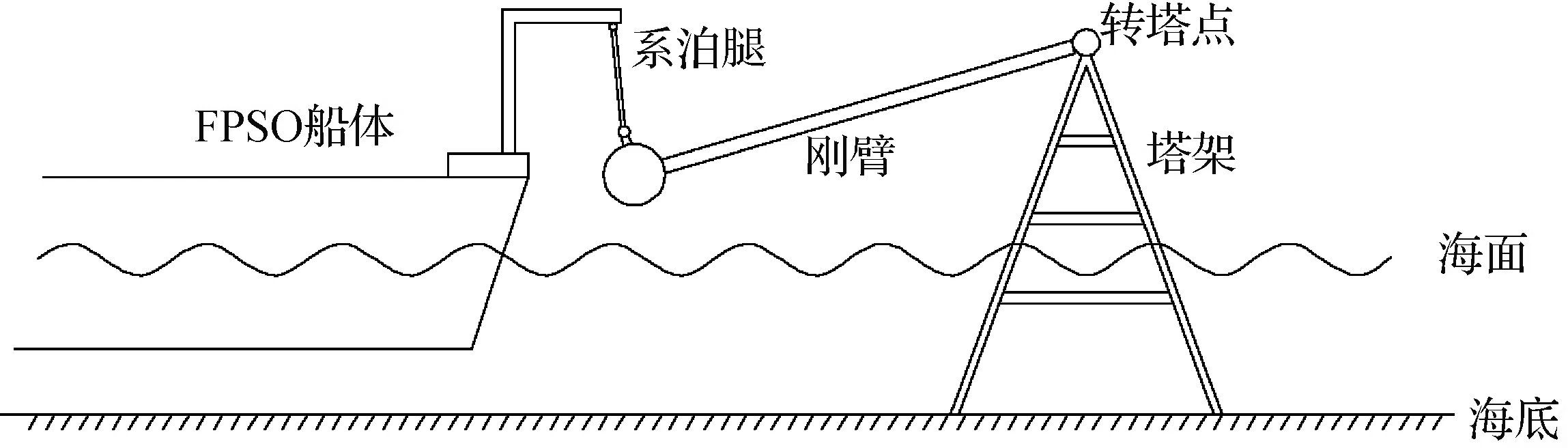
图1 软刚臂系泊系统整体示意

水上软刚臂系泊静力特性曲线光顺平滑、没有大幅冲击。同时，除了结构形式的演化，原来的浮力舱演化成了重力压载。这种系泊方式可以极大程度地避免浮力舱受到波浪的作用力使得浮力舱自身运动，从而导致结构失稳。相比之下，重力由质量结构来提供，更加稳定。水上软刚臂完全离开海面，不会受到海水的直接作用。因此对于浅海以及极浅海等海洋环境来说，软刚臂系泊系统是一种较为可靠的选择。

数值计算和模型试验是软刚臂分析中的主要手段。Xiao等[3]针对安装在浅水区域的软刚臂FPSO开展了数值和模型试验研究，探究了水深对于软刚臂系泊力的影响。通过建立具有基本动力特性的理论模型，开发数值计算程序，利用试验数据开展了对比验证。雷慧等[4]针对渤海海域FPSO，利用多体动力学的方法，应用AQWA软件研究了水深变化对FPSO水动力参数的影响。金峰等[5]针对软刚臂单点系泊系统建立了一套多体动力学模型，采用保辛数值积分方法，对FPSO的系泊响应及其系泊回复力开展了研究工作。Lyu等[6]基于多体动力学理论研究开发了一套具有7个独立自由度的多体动力学数学模型。Tang等[7]针对某软刚臂式FPSO监测数据的非平稳性，提出了一种基于非平稳响应数据的无结构响应构造方法，分析了该单点系泊结构模态参数的分布。樊哲良等[8]从应变、位移和运动姿态3个方面对渤海某FPSO的系泊力进行了讨论。苏方磊等[9]利用模型试验方法对水上软刚臂系泊FPSO的运动特性进行了探究。

优化算法和人工智能技术也在软刚臂的研究中起到积极推动作用。Lyu等通过数值模型和大尺度试验的方式，结合优化算法，对软刚臂铰接头的损伤进行了识别[10-11]。赵梓舒[12]采用Adams软件开展了软刚臂有限元模拟，采用堆栈稀疏自编码网络对软刚臂系泊系统铰接点损伤开展了识别分析。韩宇等[13]采用深度学习中的LSTM方法对软刚臂系泊力的预测方法进行研究。

针对软刚臂系泊系统的研究大多是针对其动力性能进行的，这种方法可以探究软刚臂系泊系统的性能能否达到最优化。水上软刚臂系统不受流体载荷影响，静力分析是快速评估其系泊力的重要手段。因此在设计之初需要对软刚臂系统的静力特性进行分析，这样可以对设计出来的结构进行受力和强度的评估。此外，静力特性分析可以求解软刚臂的静力刚度情况，能够为软刚臂动力分析打好基础。范模[14]从系泊特性计算的角度对软刚臂系统进行了静力受力分析。李欣等[15]针对软刚臂系泊系统进行了静力分析，得到了纵向以及垂向的刚度曲线，为模型试验提供了校验依据。胡勇等[16]针对塔架软刚臂单点系泊系统进行了静力分析，得到了FPSO纵向运动时的系统刚度。然而FPSO软刚臂系统的形式多种多样，同一种分析方法无法做到适合所有类型的软刚臂系统。

针对某FPSO软刚臂系泊系统进行研究，形成了一套压载舱式水上软刚臂单点系泊系统二维静力平衡计算方法，通过这一方法可以解析计算分析软刚臂上各点处受力情况，并能够用来对商业软件的静力分析结果进行验证和校核。文中选取了某FPSO压载以及满载工况，通过Fortran编程对理论公式进行计算分析，并与OrcaFlex等商业软件的数值模拟结果、试验结果进行分析和比较，对静力分析结果进行了验证。

1 软刚臂系泊系统的基本结构

研究对象为某FPSO塔式软刚臂单点系泊系统。软刚臂结构分为：系泊腿、YOKE(即刚臂、刚性轭架)和转塔3个部分。系泊腿为对称结构，上端与船体相连，下端连接YOKE；YOKE连接着转塔和系泊腿，在转塔上有3个自由度。YOKE和系泊腿的示意如图2和图3所示。

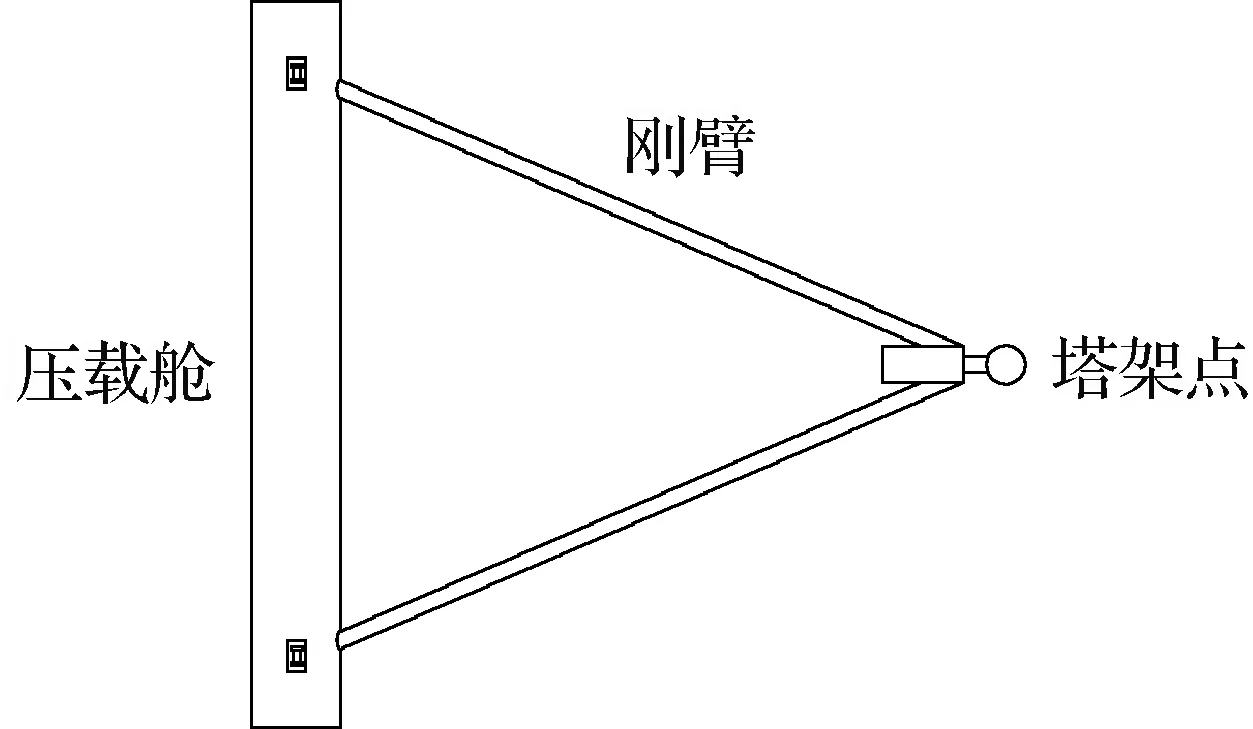
图2 YOKE俯视图

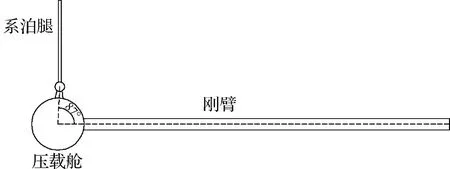
图3 系泊腿和YOKE的侧视图

2 软刚臂系统二维静力平衡理论

2.1 软刚臂二维静力平衡理论的假设

在分析FPSO系泊系统在波浪作用下的运动响应时，引入如下基本假设：1)刚体假设，FPSO为刚体，会产生6个自由度的运动；2)软刚臂两条系泊腿平行，且二者运动也完全相同，这样可以保证两条系泊腿关于同一平面对称；3)海底不可变形和渗透。基于以上假设，在分析的过程中，将两条系泊腿转化到某一平面内，从而将整个软刚臂系泊系统由三维状态简化为二维平面模型，方便对其进行受力分析。

2.2 软刚臂二维静力平衡理论

进一步从软刚臂的结构特点和受力特性进行分析。首先对软刚臂结构进行拆分，在系泊腿铰接处，按照此处无弯矩、作用力与反作用力相等的原则，将软刚臂整体结构的受力(图4)拆分成系泊腿受力分析(图5)、YOKE和压载舱等附属结构的受力分析(图6)。

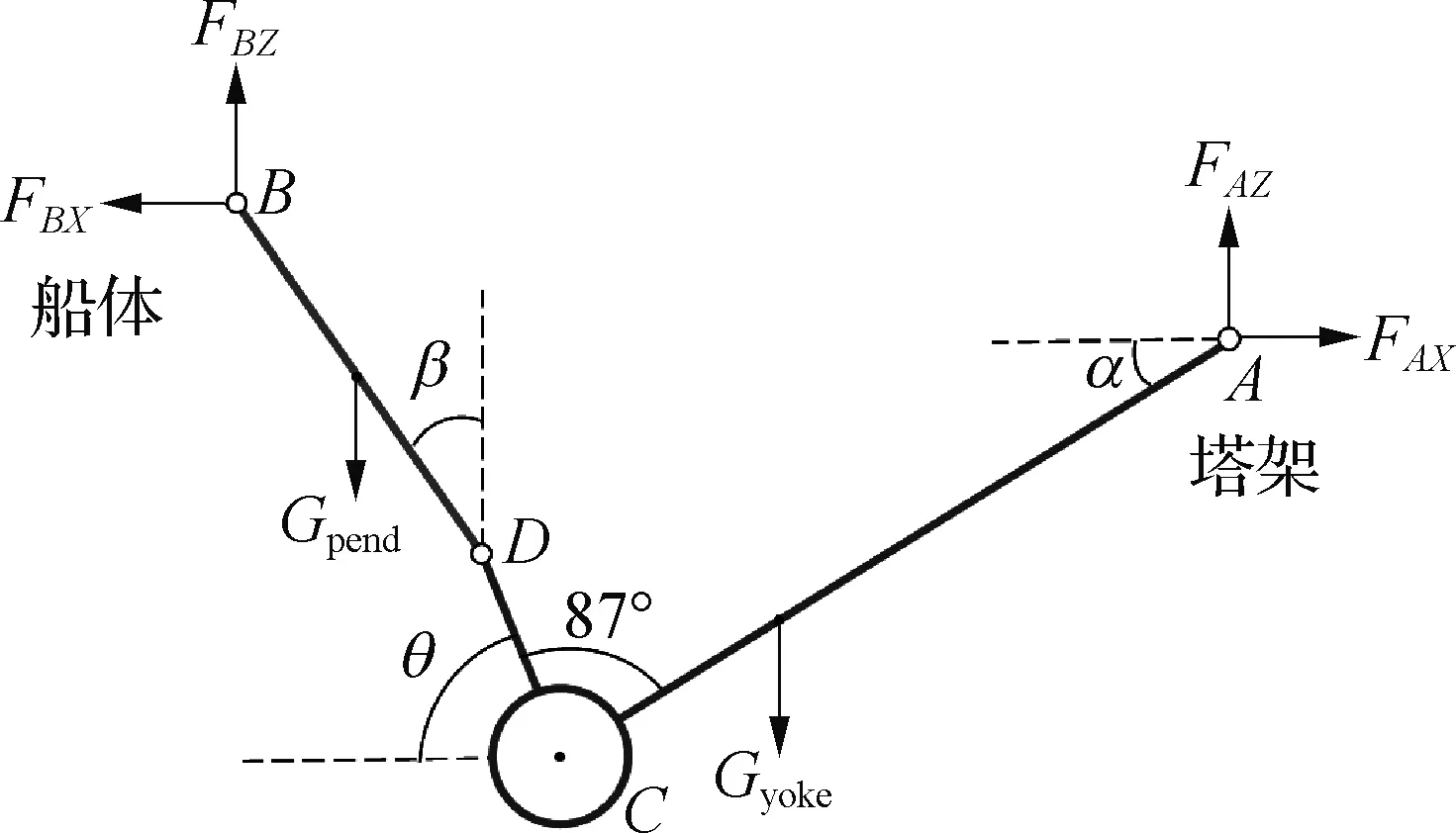
图4 整体结构受力分析简化图

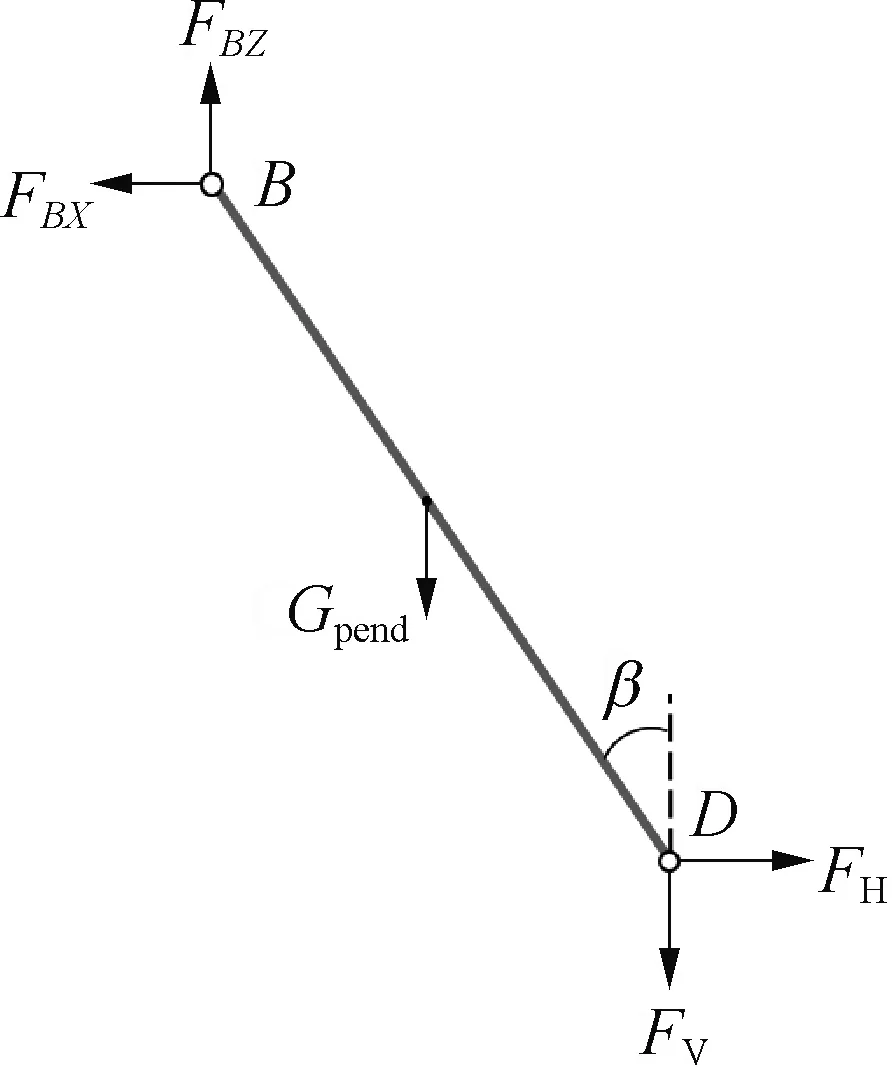
图5 系泊腿受力分析简化图

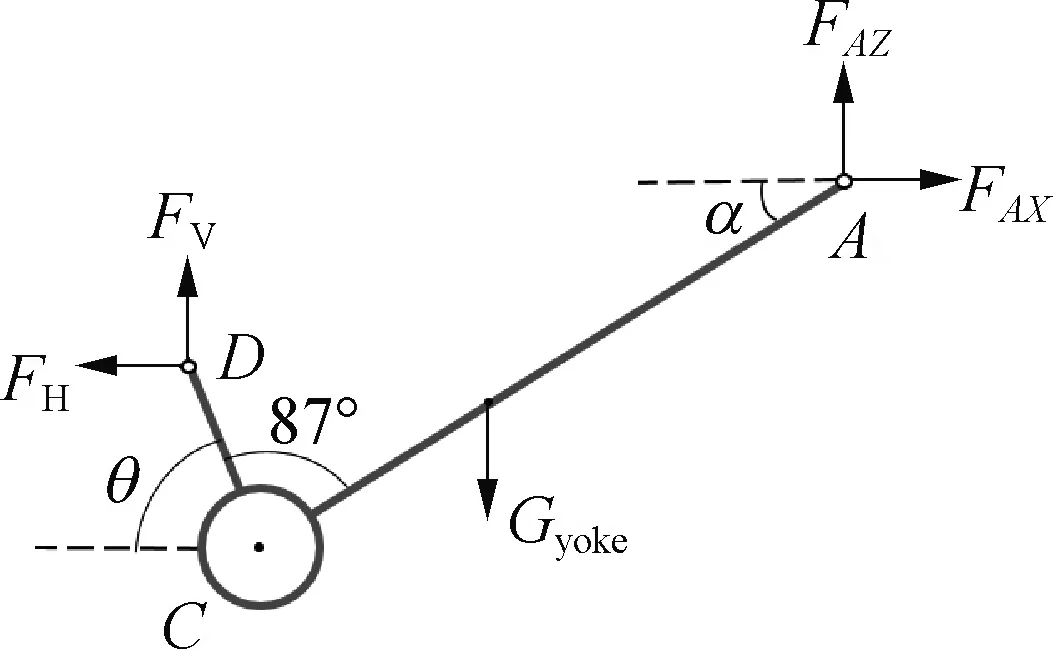
图6 YOKE受力分析简化图

对于图4，以系泊腿上端点B为中心取矩，根据受力平衡可得：

(1)

对于图5，以YOKE连接点A为中心取矩，根据受力平衡可得：

(2)

式中：Gpend为系泊腿的重力，Gyoke为YOKE连同压载舱的重力，FV为系泊腿下端点处的垂向受力大小，FH为系泊腿下端点处的水平向受力大小，FBZ为系泊腿上端点处的垂向受力大小，FBX为系泊腿上端点处的水平向受力大小，FAZ为YOKE与塔架连接点处的垂向受力大小，FAX为YOKE与塔架连接点处的水平向受力大小；LBD为系泊腿的长度，Lkg为YOKE连同压载舱重心距A点的长度，LAC为压载舱中心距YOKE头的长度，LCD为压载舱中心到系泊腿下端点的距离；α为YOKE与水平方向的夹角，β为系泊腿BD与垂直方向的夹角，θ为系泊腿下端点D到压载舱中心C点的水平方向夹角。取含有FV和FH的两个式子如下：

(3)

将式(3)整理得：

(4)

根据已知条件，有如下关系：

Lkg=LAC-rtk

(5)

式中：rtk为压载舱的半径；这里选取的软刚臂结构中∠ACD=87°，即θ=180°-87°-α；LCD的长度是一个固定值。通过式(4)和式(5)中的已知条件可以求得YOKE连接点A和系泊腿上端点B在X方向和Z方向上的力：

(6)

每条系泊腿上端的张力大小Tpend为：

(7)

这样，通过式(4)、式(6)和式(7)可以得出：1)已知θ的大小即可求出水平方向的夹角α的值；2)给定α、β可得出系泊腿上端点处(以及塔架上端点)水平和垂直方向力的大小；3)系泊腿的张力可以由系泊腿顶部B点处的水平和垂向力推导求出。

3 软刚臂静力特性计算

3.1 软刚臂OrcaFlex模型

利用OrcaFlex软件实现软刚臂系统静态的分析过程。其中，软刚臂系统在OrcaFlex软件中的主视图如图7所示。在OrcaFlex软件建立FPSO系泊耦合模型过程中，FPSO船体用Vessel单元模拟，船体支架使用不考虑质量的6D Buyo单元模拟，支架质量和重心已经包含在FPSO船体中，系泊系统的左右系泊腿用Line模型，软刚臂用6D Buyo单元模拟，塔架使用6D Buyo单元、Shape单元和Constraint单元模拟，在文中塔架不考虑质量和受力影响，仅作为系泊系统在计算时围绕的固定点的示意，塔架对计算结果不产生任何影响。

图7 OrcaFlex中软刚臂的主视图

建立了OrcaFlex计算模型之后，分别在FPSO满载和压载条件下对OrcaFlex的静力计算结果以及理论推导结果进行分析和比较，同时与已有的SESAM Simo计算结果数据进行对比分析，从而验证理论推导的准确性。此外，基于已有的压载工况软刚臂水池模型试验数据，进一步对比分析商业软件和理论分析的计算结果。图8为水池试验现场图。

图8 水池试验现场图

3.2 静力对比分析

3.2.1 满载条件

通过软刚臂二维静力平衡理论计算出的YOKE与水平方向的夹角、系泊腿垂直方向的夹角、系泊腿的张力以及塔架上X与Z方向上的分力与OrcaFlex软件算出的结果、SESAM Simo模拟的结果作对比。首先考虑FPSO在满载条件下的情况，对比与误差如图9至图13所示，计算数据如表1至表5所示。

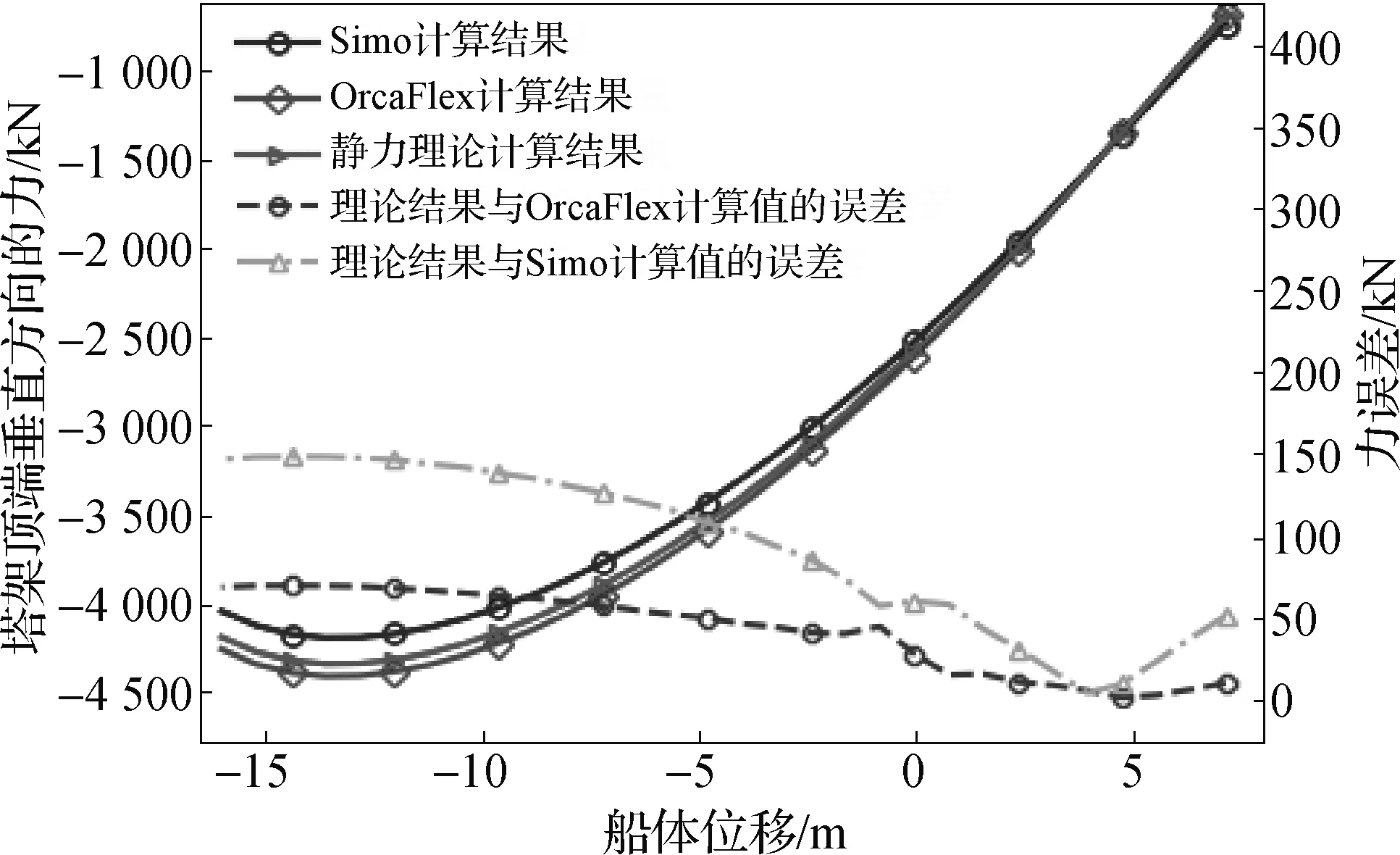
图13 满载时塔架Z方向力对比

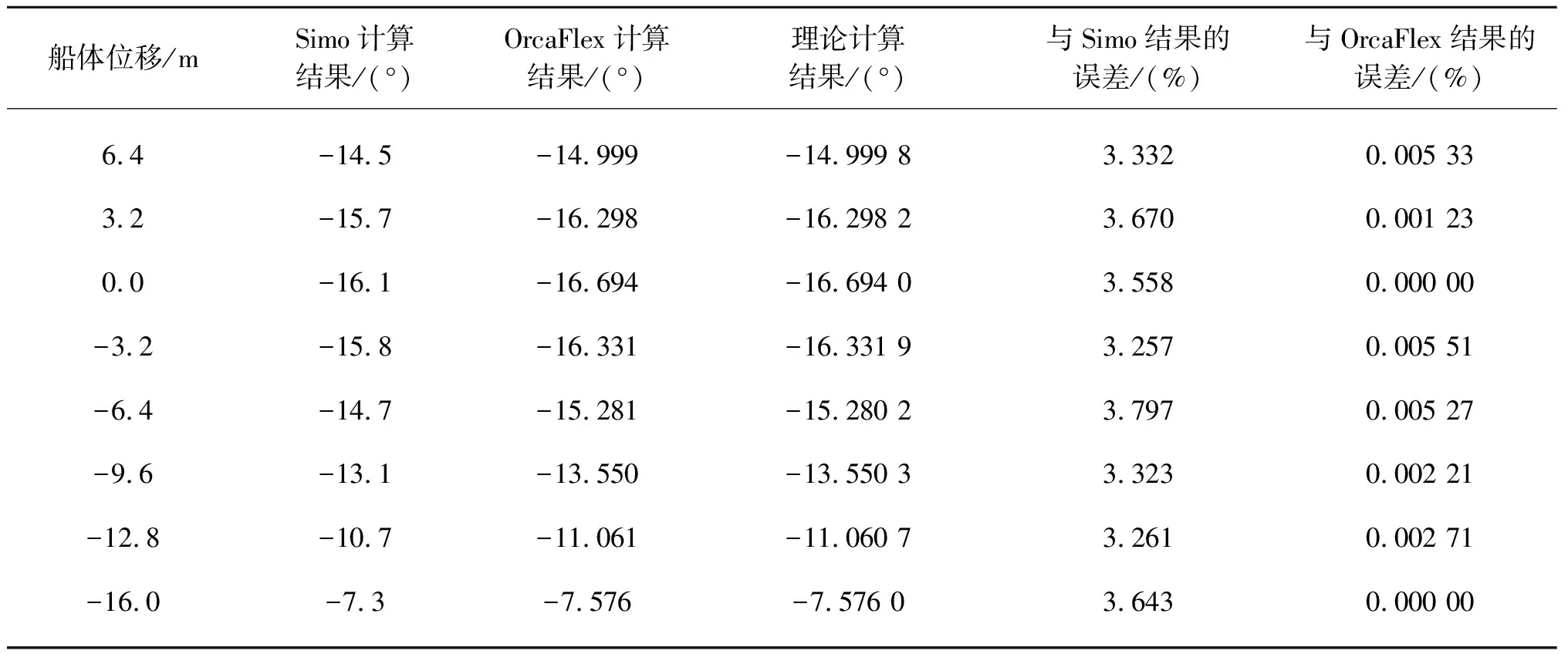
表1 满载时水平方向夹角的计算值及误差

从图9的对比中可以看出，水平方向夹角的理论计算结果与OrcaFlex的计算结果吻合良好；与Simo计算结果有着3.5%左右的误差，船体位移为-6.4 m时，理论计算结果与Simo结果相差最大，约3.797%，这样的误差属于可接受范围内。

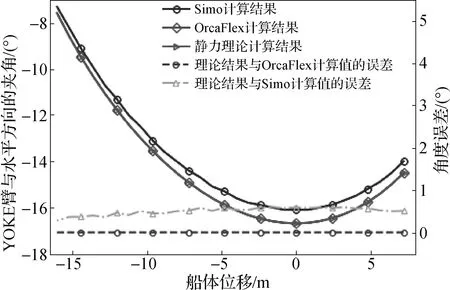
图9 满载时水平方向夹角对比

从图10的对比以及表2的数据中可以看出，在计算垂直方向夹角时，理论计算结果与OrcaFlex和Simo的计算结果吻合良好，误差不超过1%。在船体位移接近0 m时，系泊腿与垂直方向的夹角将趋近于0°，图10中仅展示绝对误差的大小，表2中数据为相对误差值。

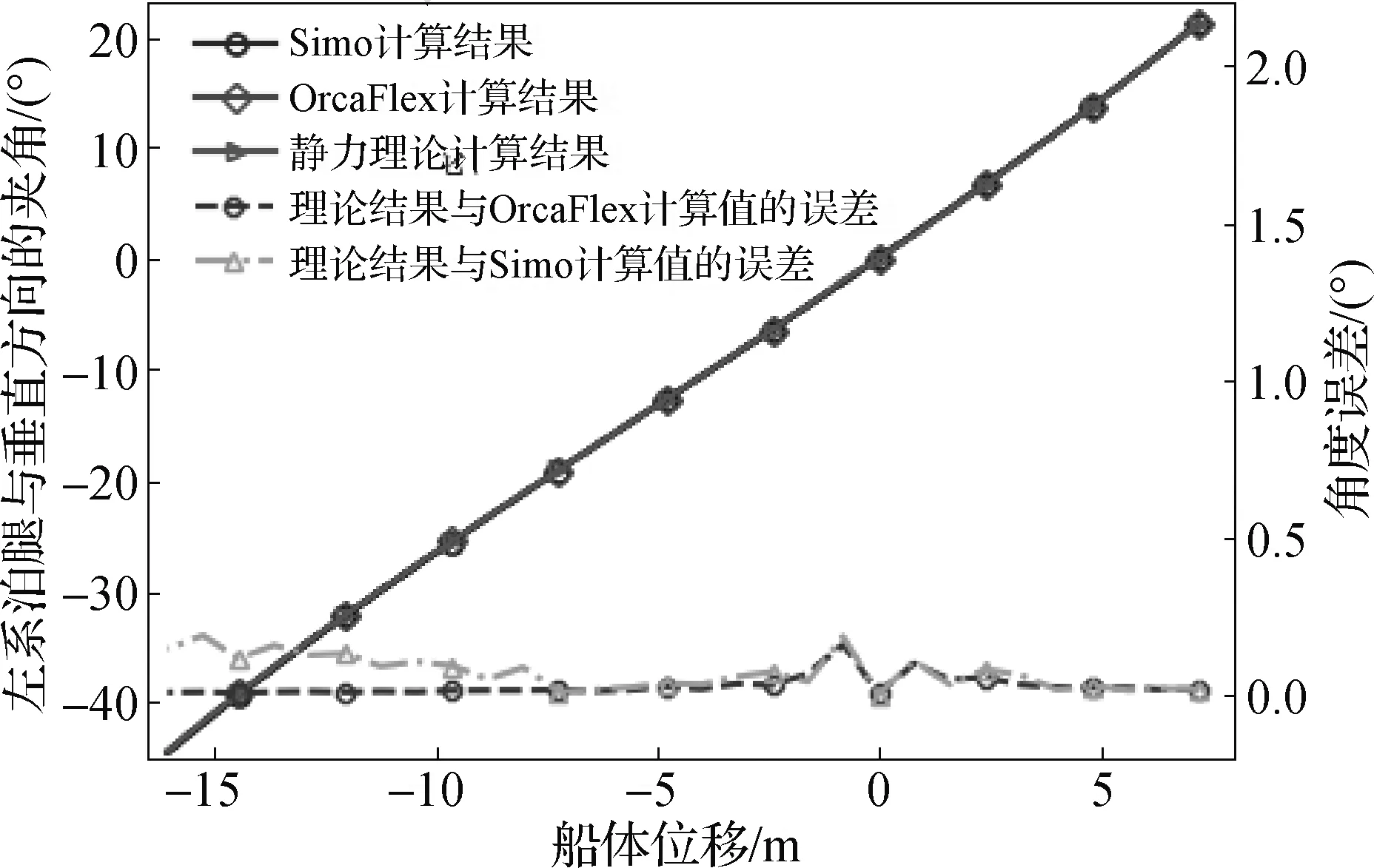
图10 满载时垂直方向夹角对比

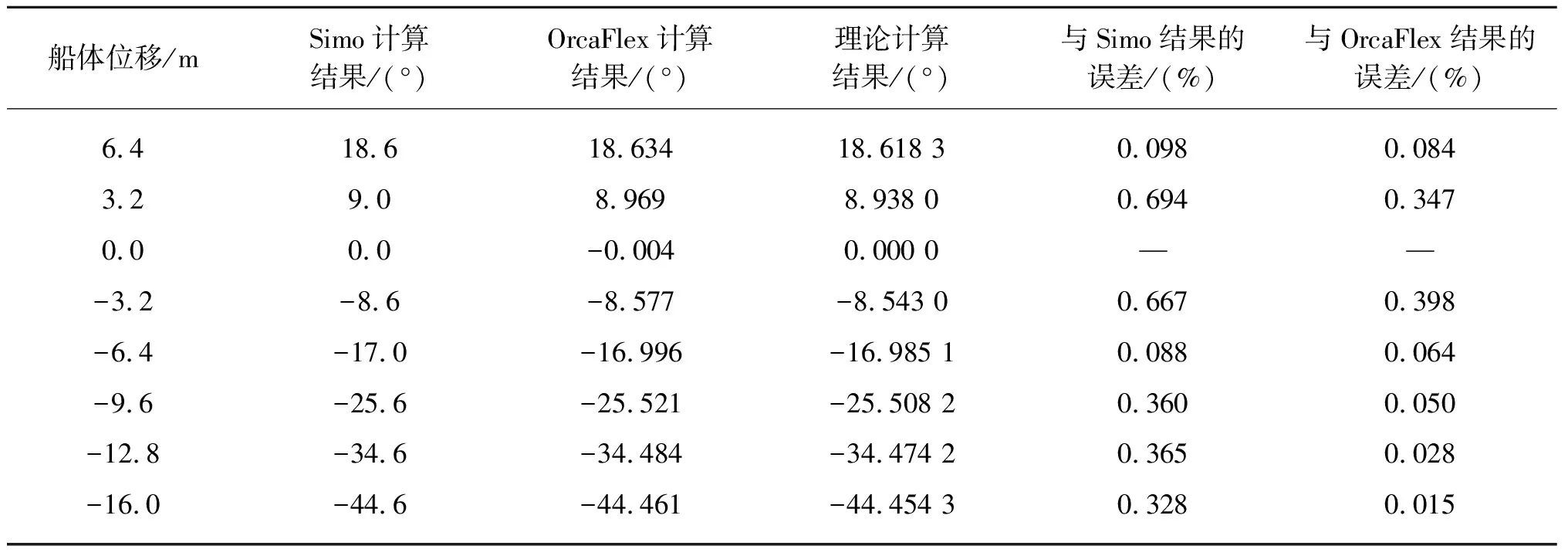
表2 满载时垂直方向夹角的计算值及误差

在二维静力平衡理论的推导当中，水平及垂直方向夹角是得到各项力计算结果的基础。而从图9及图10的误差对比来看，理论计算得到的角度结果与OrcaFlex计算的角度结果误差极小，说明与OrcaFlex结果的对比是有意义的。

从图11的系泊腿张力对比图和表3中可以看出，理论计算结果与OrcaFlex和Simo的计算结果有着一定的差距。

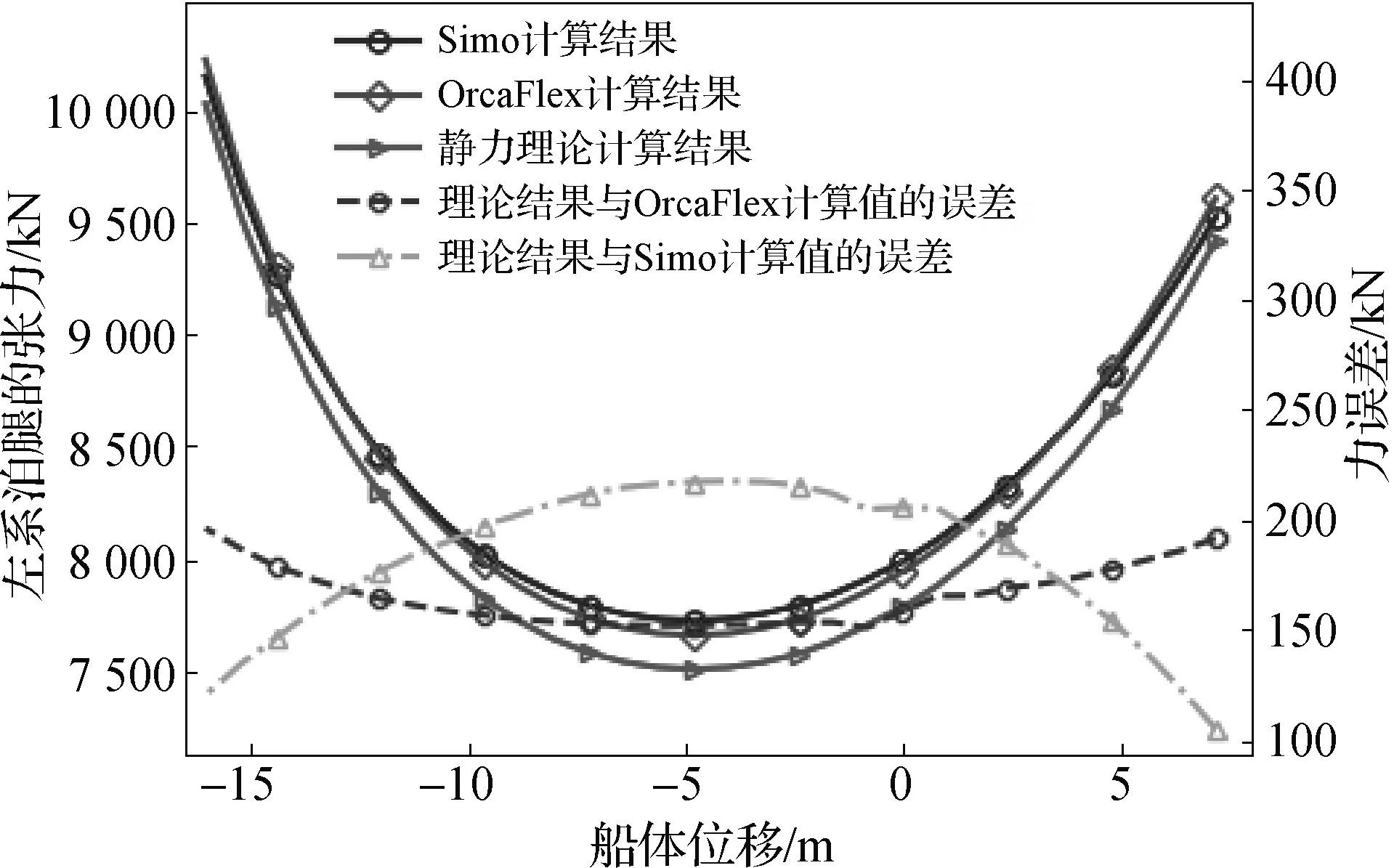
图11 满载时系泊腿张力的对比

系泊腿张力较小时，理论计算结果与OrcaFlex结果的误差较小，但与Simo结果的绝对误差较大。从表3的数据中可以了解到，理论计算结果与两种软件计算结果的相对误差仍然保持在3%以下，处于误差允许的范围内。

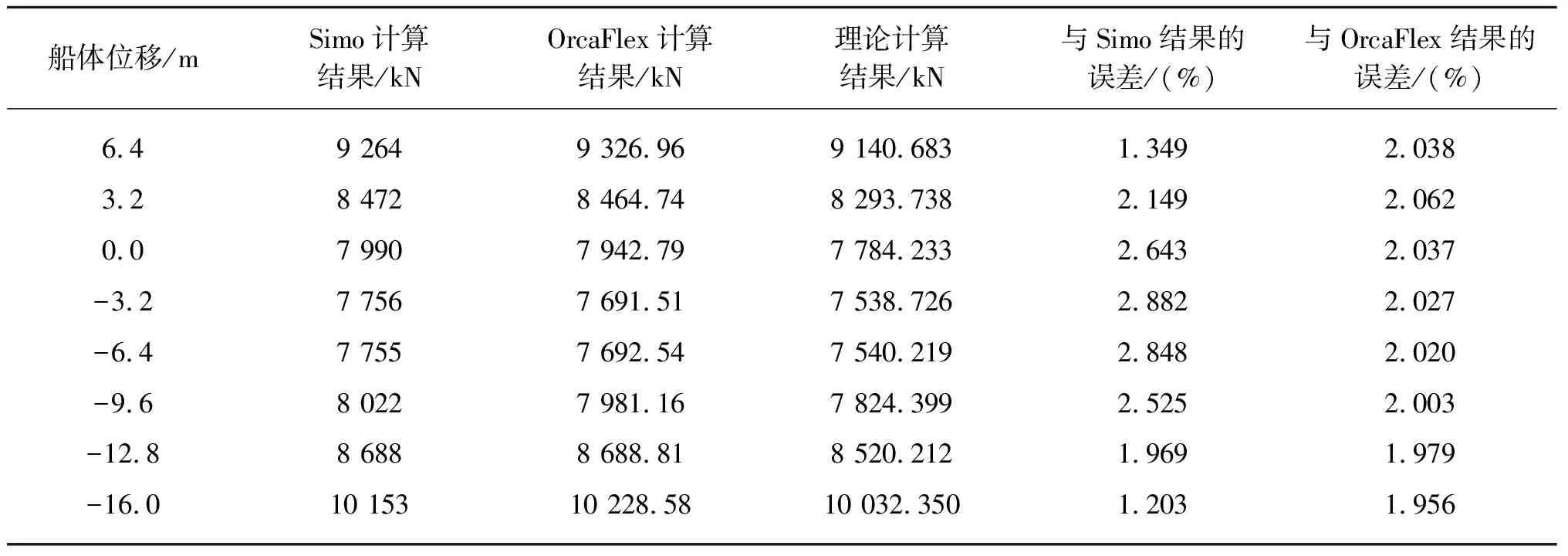
表3 满载时系泊腿张力的计算值及误差

从图12和表4中可以看出，在计算塔架X方向力时，3种计算方法的结果基本吻合，理论计算结果与商业软件计算结果的误差约为2%。与垂直方向夹角相同的是，在船体位移为0 m时，塔架X方向的力也趋近于0 kN。随着船体向两个方向移动，计算结果的绝对误差也随之增加，而相对误差则变化不大。

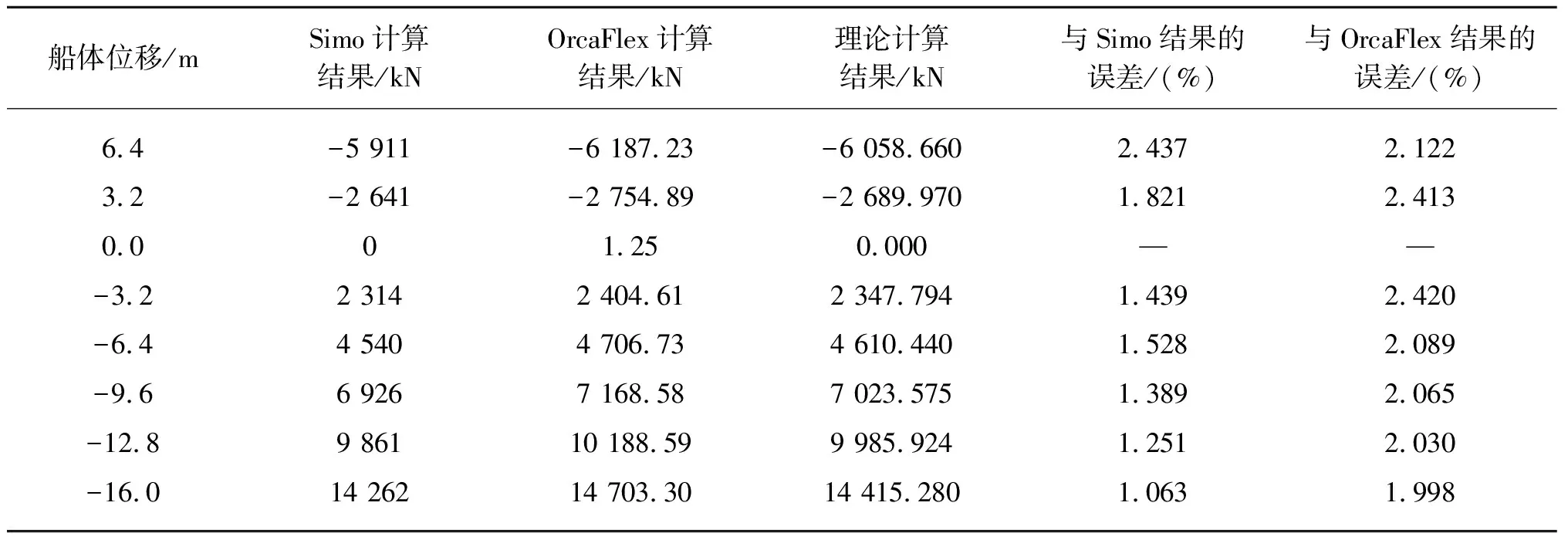
表4 满载时塔架X方向力的计算值及误差

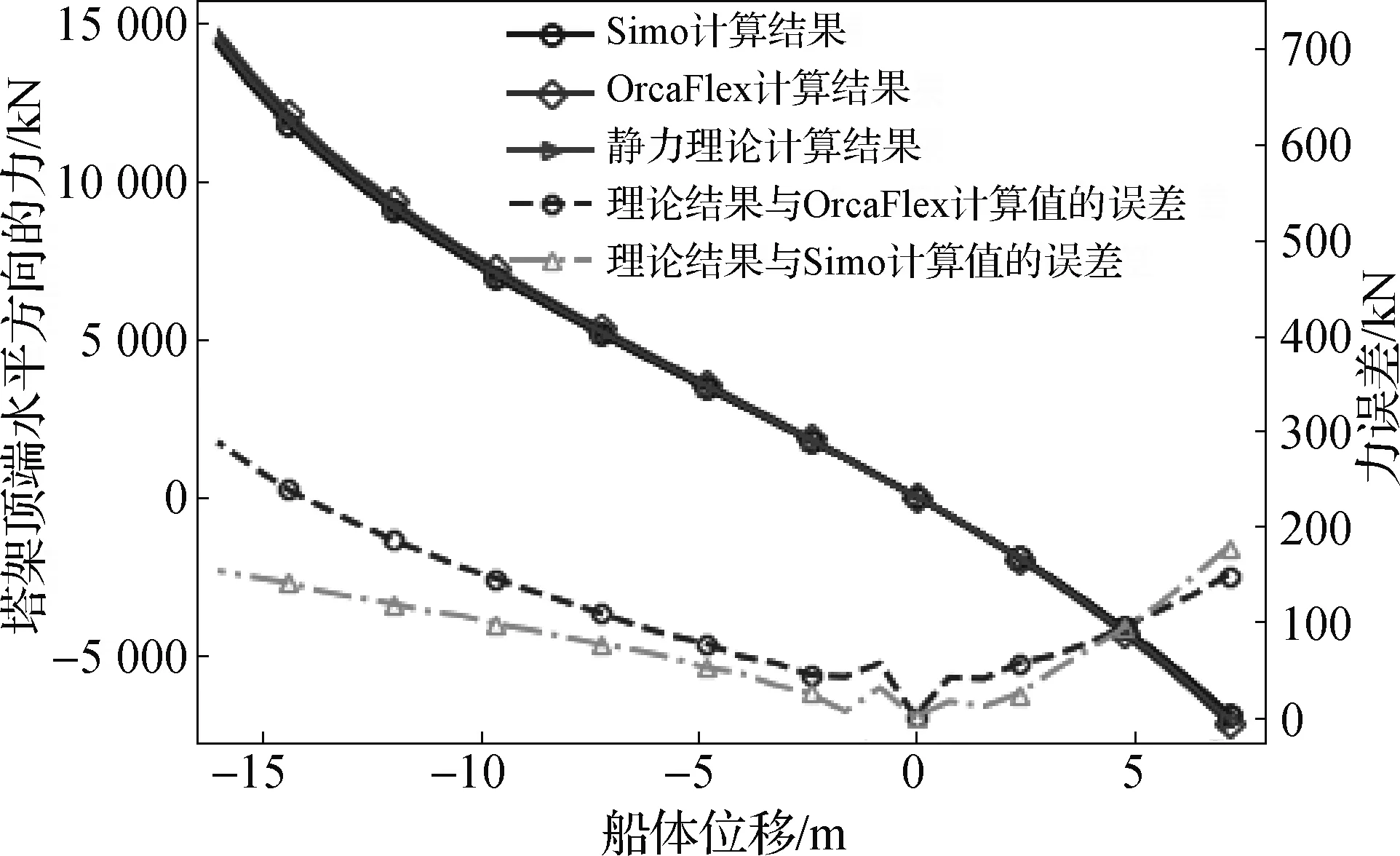
图12 满载时塔架X方向力对比

从图13和表5中可以看出理论计算结果与OrcaFlex的计算结果相差不大，相对误差在1.5%左右；但是与Simo的计算结果相差较大，最大相对误差超过了4%。

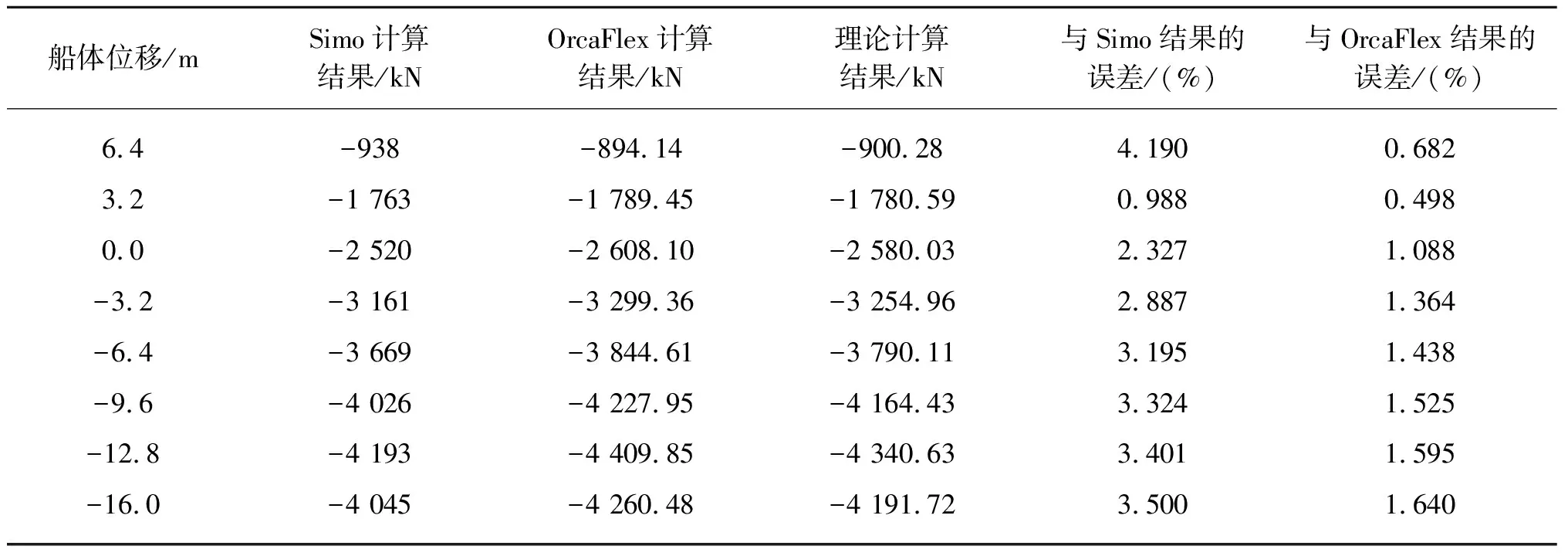
表5 满载时塔架Z方向力的计算值及误差

从以上比较可以发现，所提的软刚臂二维平衡理论计算结果与OrcaFlex计算结果吻合较好，相对误差大部分都保持在3%以内，只有塔架水平方向力的误差较大。而理论计算的结果与SESAM Simo中结果的相对误差约为3%～5%，系泊腿的张力以及塔架在Z方向的分力随FPSO纵荡位移的变化曲线与SESAM Simo结果存在较大误差，但其相对误差不超过5%，属于在允许范围之内。

3.2.2 压载条件

在考虑船体的压载条件下，将理论计算结果与Orcaflex软件计算结果、SESAM Simo软件计算结果和水池试验的数据进行对比，如图14至图18所示。图14所示为压载条件下，3种方法计算YOKE水平方向夹角的对比。由于在水池试验当中对YOKE水平方向的夹角获取较为复杂，试验数据中并未记录水平方向夹角，因此图14中仅由3条曲线进行对比。从图14中可以看出，理论计算结果与OrcaFlex计算结果吻合良好，与Simo的结果约有3%的误差。

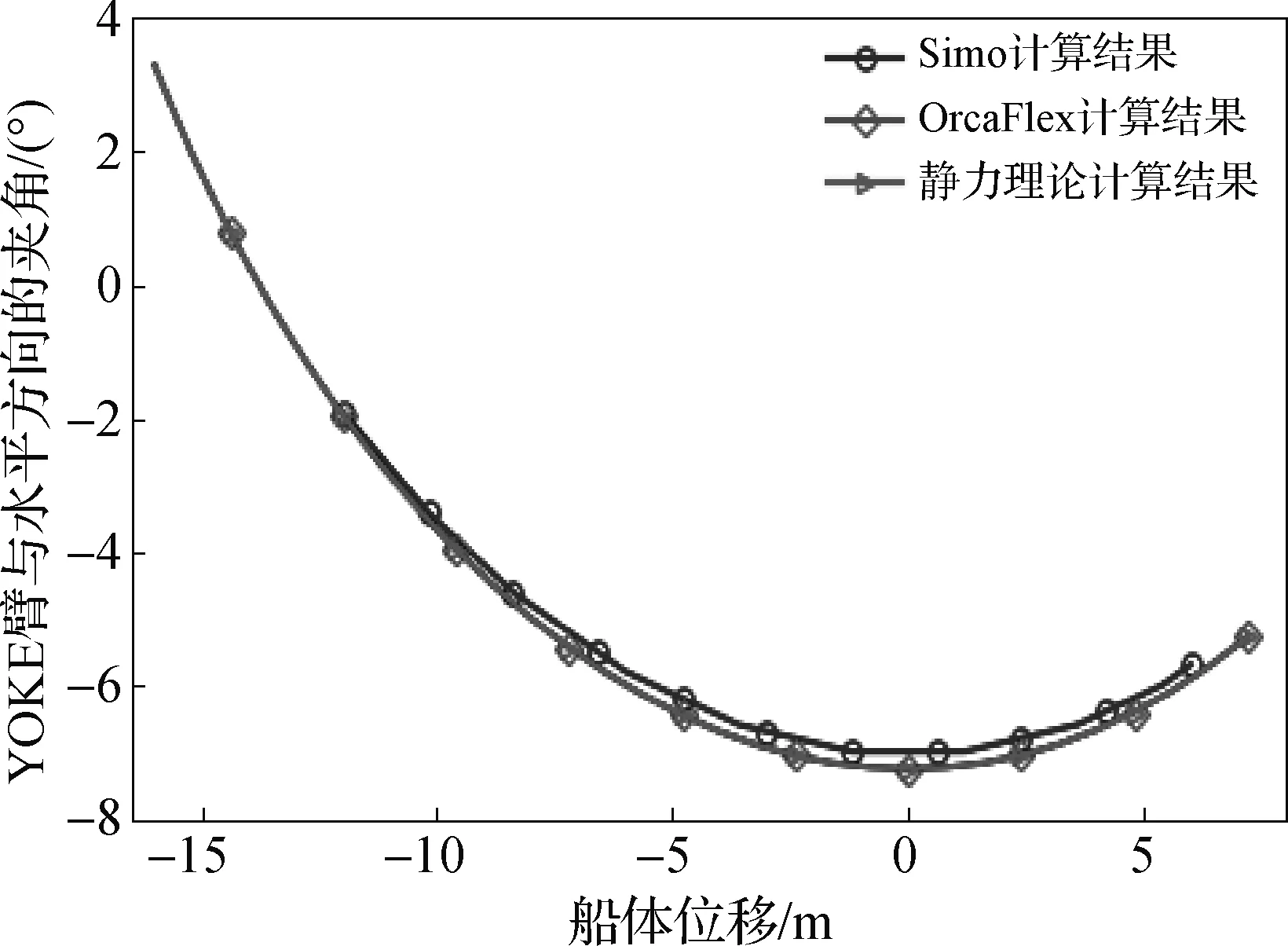
图14 压载时水平方向夹角对比

图15为垂直方向上3种计算方法的计算结果与试验数据的对比。从图15中可以看出4条曲线的吻合度很高，相互之间相对误差不超过1%。从系泊腿张力对比图16可以看出，静力理论计算结果要略小于OrcaFlex以及Simo的计算结果，误差约为3%；理论计算结果与试验结果的误差较大，约为5%。船体位移大于15 m之后，静力理论计算结果与OrcaFlex计算结果的误差明显减小。

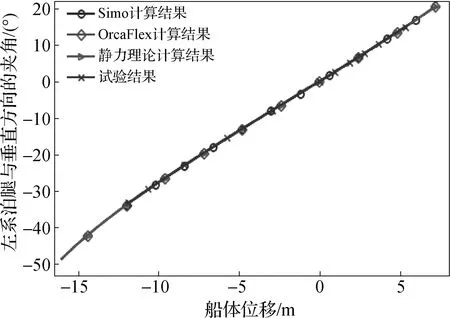
图15 压载时垂直方向夹角对比

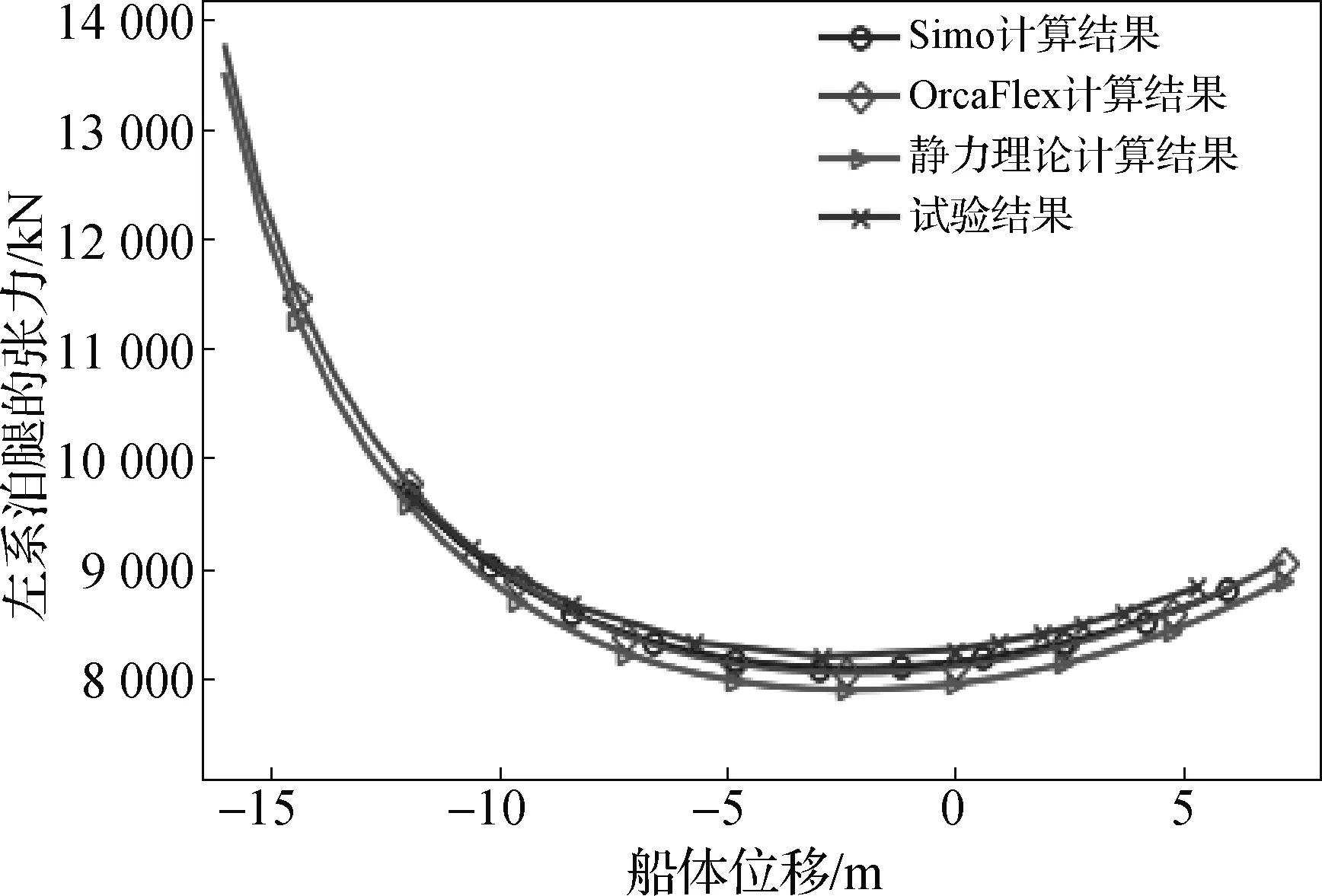
图16 压载时系泊腿张力的对比

对于压载条件下塔架顶端水平方向的力而言(图17)，3种计算结果的曲线与试验数据曲线吻合良好，相对误差为2%左右。而在船体位移大于10 m时，试验结果曲线有逐渐偏离静力理论计算结果曲线的趋势，此时的相对误差仍为2%。图18为塔架垂直方向力的对比，可以看出，静力理论计算结果曲线与OrcaFlex计算结果曲线拟合较好，相对误差约为2%；与Simo计算结果的相对误差约为3%；试验结果曲线与另外3条曲线的偏差较大，但变化趋势与其它曲线相同。

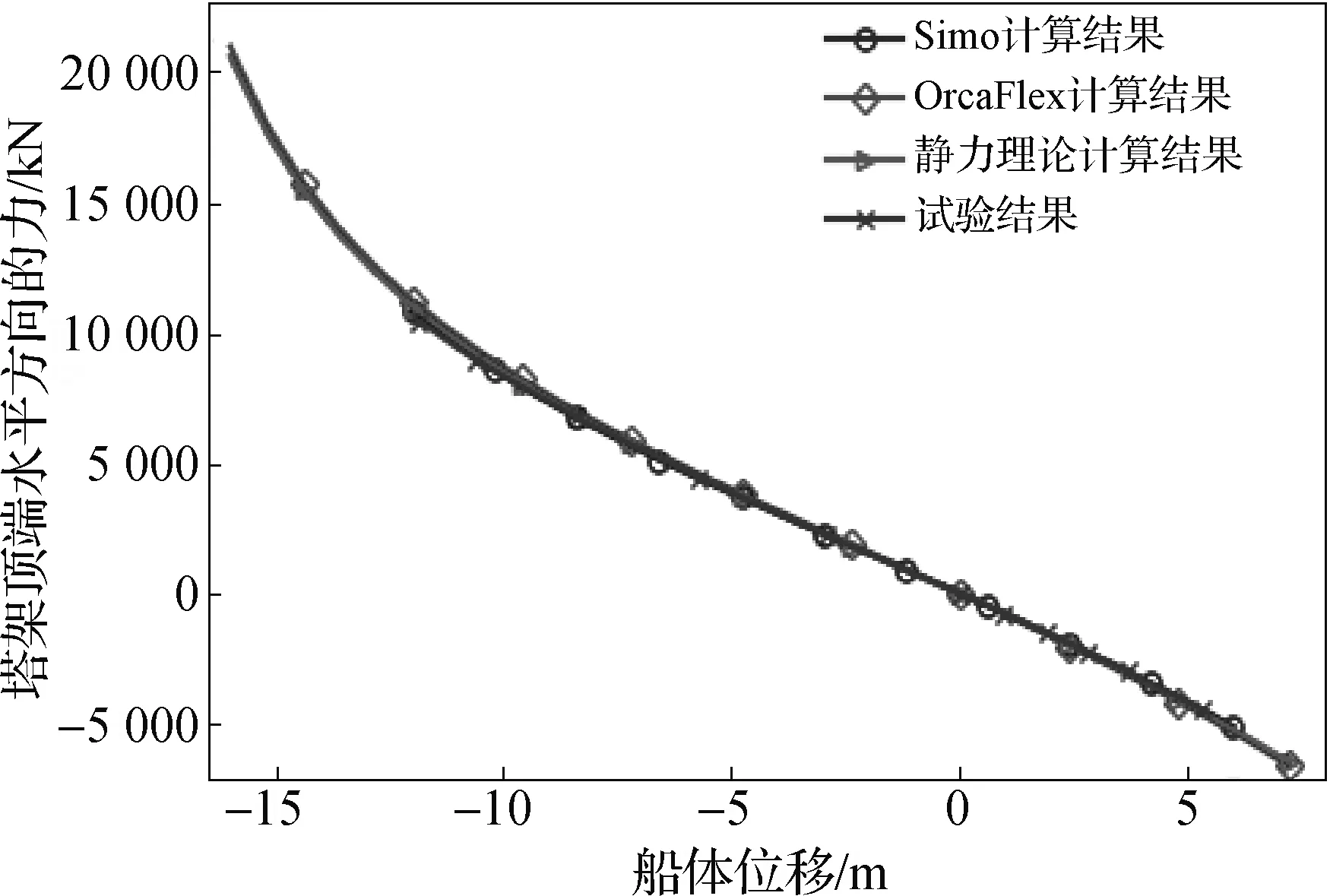
图17 压载时塔架X方向力对比

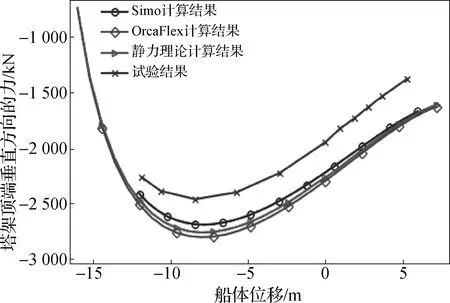
图18 压载时塔架Z方向力对比

由数值与试验对比中可以看出，在垂直方向夹角和塔架X方向力上，几种计算方法的结果几乎一致；在水平方向夹角与系泊腿张力上，理论计算值与软件计算结果存在一定误差；而对于塔架Z方向力，试验值与理论计算值以及软件计算值有着较大误差。软刚臂锚泊系统模型试验搭建和标定较为困难，船体绕单点也容易产生转动，试验开展起来影响因素较多，因此试验获得精确值的概率不高，但是试验仍然能够较为准确地反应系泊力的变化趋势。从图18来看，误差总体变化稳定，可以辅助佐证理论计算的准确性。

总体而言，理论分析计算结果与两种软件的计算结果以及试验的部分结果都能良好吻合，充分证明了理论计算结果对FPSO软刚臂系统模拟的准确性和可靠性，为后续的时域计算分析打下了很好的基础。

4 结 语

针对某软刚臂式FPSO，建立了压载舱式水上软刚臂单点系泊系统二维静力平衡计算公式，并采用OrcaFlex等商业软件对理论计算结果与数值计算结果开展了对比分析。另外，还通过与水池试验的数据进行对比，进一步验证了分析结果的准确性。

在FPSO的软刚臂系统静力分析中，在船体纵荡位移方向，软刚臂结构静力公式推导的结果与OrcaFlex软件计算得到的刚度回复力曲线吻合良好且两条曲线基本一致，与SESAM Simo计算结果相比趋势一致，系泊水平力吻合良好，倾角略大于Simo计算值，在允许误差范围内。以上结论可以证明文中推导出的软刚臂单点系泊系统静力分析公式的准确性。利用这一公式，可以对软刚臂系泊系统静力刚度进行分析和计算，为进一步分析软刚臂系统的动态稳性做好了铺垫。