图论与传球网络相融合的教学探究与实践

刘泽婷， 葛焕敏， 沈燕飞

(北京体育大学 体育工程学院，北京100084)

1 引 言

图论在生活中应用广泛，特别地近年来逐步成为人工智能与机器学习的基础核心模块.本文主要结合自身的教学实践探究图论与基于传球网络的运动表现分析相融合，探究新工科背景下体育院校的新教学模式，同时也将体教融合理念深入到教学中.

图论以图为研究对象，图是由若干给定的点及连接两点的线所构成的图形，通常用来描述某些事物之间的某种特定关系.图论是应用数学中重要的知识结构，著名的哥尼斯堡七桥问题、中国邮递员问题和货郎担问题等都是图论中的经典问题[1].关于图论的教学，不同专业领域的教师融合学生的专业背景已经做了丰富调研、探究与改革，如防空兵遂行战备和作战中的兵力配置[2]，葫芦归罐罐归篓，狼羊过河等童年时期的智力题或故事[3].然而融合体育领域专业知识的图论教学案例比较少，但是这种案例对新工科背景下体育院校的工科专业学生具有非凡意义.本文主要以传球网络为例介绍图论在体育领域中的应用，一方面打破了枯燥的单纯学习图论知识点，一方面开拓了学生的视野，进一步了解新型体育科技，更重要的是让学生更加清晰地认识自己的专业，提升学生学习交叉学科知识和从事研究、开发新型体育科技的兴趣，通过了解图论在体育领域中的应用，激发学生从事体育科技事业的动力.

2 图的相关概念与足球传球网络相融合

在讲完图的基本概念，集合表示及图形表示之后，以传球网络为例，介绍图论在运动项目研究中的应用.传球网络是体育领域中一个重要的技术工具，特别是面向竞技体育.传球网络作为比赛运动表现分析的一个技术工具，目前广泛应用于预测比赛结果[4-5]、表征球队比赛风格[6]和识别球场上的关键球员或关键区域[7-8].例如在预测比赛结果方面，利用传球网络找到获胜球队在队友配合、传球方式、网络结构等方面的共性特点，根据总结出的特点，可以帮助预测比赛的结果.胜率较高的球队往往有着更高的网络密度、接近中心性，以及更多的总传球数[4-5].

事实上传球网络构建的理论基础是图论. 例如基于无向图和有向图的定义、顶点和边的关系、子图、平行边、度数和图的连通性等理论知识， 融合足球运动自身的特征建立足球传球网络.下面以三种传球网络介绍图论在体育领域中的应用，通过球场、球员和传球这三个因素与图的位置、顶点和边相呼应，引入三种传球网络，会发现每一种传球网络都以图论的相关知识作为理论支撑，同时将传球网络与图论的相关理论相结合研究运动表现分析，如预测运动项目的比赛结果、表征球队比赛风格和识别球场上的关键球员或关键区域.

2.1 球员传球网络——图论相关的基本概念

球员传球网络[9]只关心传球者，即谁传了球，不关心每一次传球的位置，如图1.首先，基于传球网络，引入图的相关概念.图1中球队阵型中球员站位是网络节点，即图的顶点；两个球员之间发生了传球，形成网络中的连线，即图的边.如果在传球网络中不关心球员传球的方向，例如无论球员A向球员B传球还是球员B向球员A传球，都只用一条无向边表示，此时基于传球网络生成的图为无向图.如果在传球网络中只关心球员之间的传球方向，例如球员A向球员B传球，用一条从A指向B的有向边表示，此时基于传球网络生成的图为有向图.本文主要以无向图为例，传球网络中连线有粗有细，其代表图的平行边.若传球网络中发生多次传球，其代表图的多条平行边.进一步基于传球网络引入图的度数，即顶点作为边的端点的次数.

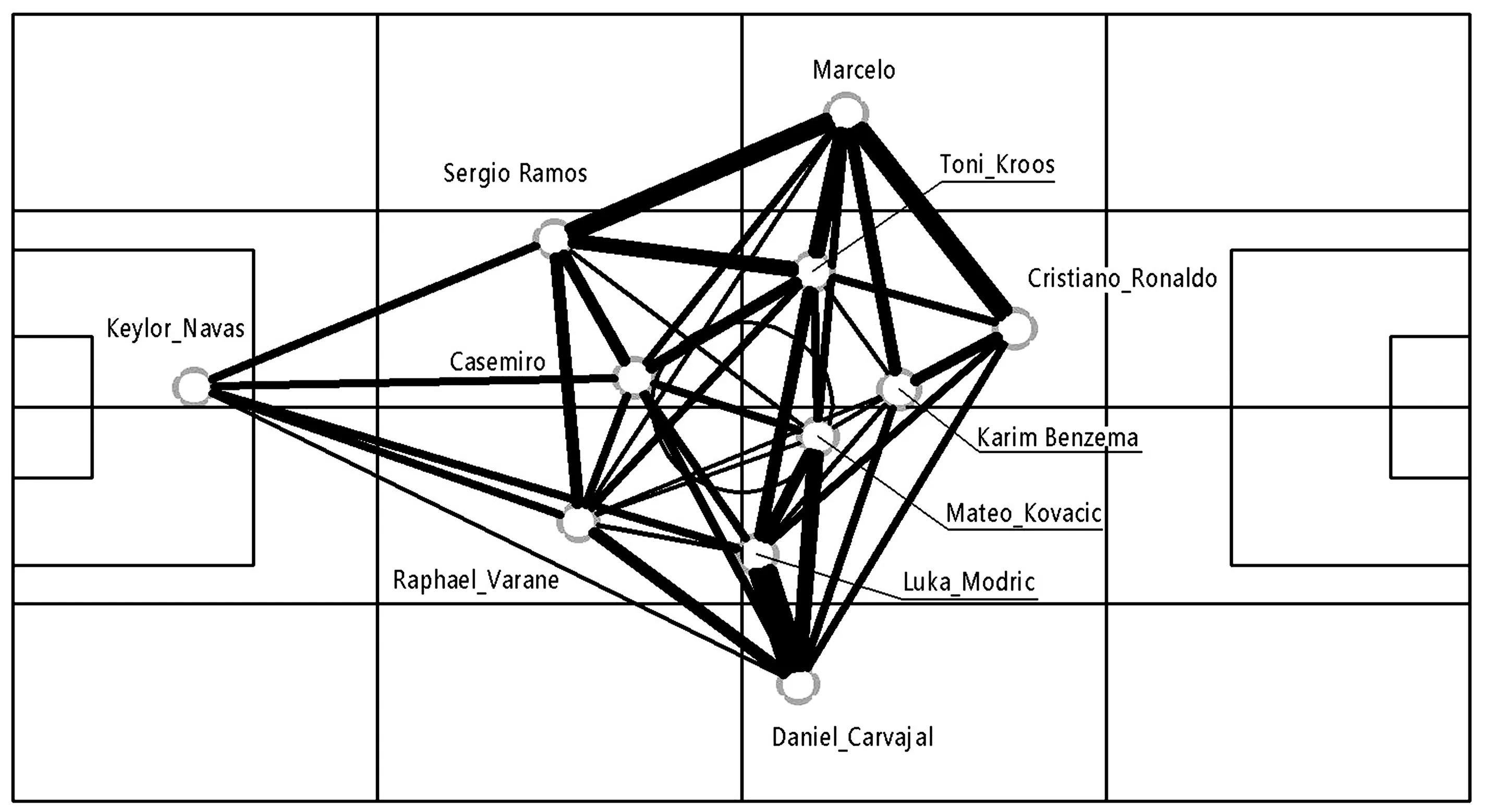
图1 2017/2018赛季，西班牙足球联赛“西甲”皇家马德里队的传球网络

2.2 球场区域传球网络——子图

球场区域传球网络[10]只关心发生传球事件的区域，即在哪里传了球，而不关心传球者是谁，如图2.图2中球场被划分成9个区域，以球场划分的区域作为网络节点，形成一个球场区域传球网络见图3.

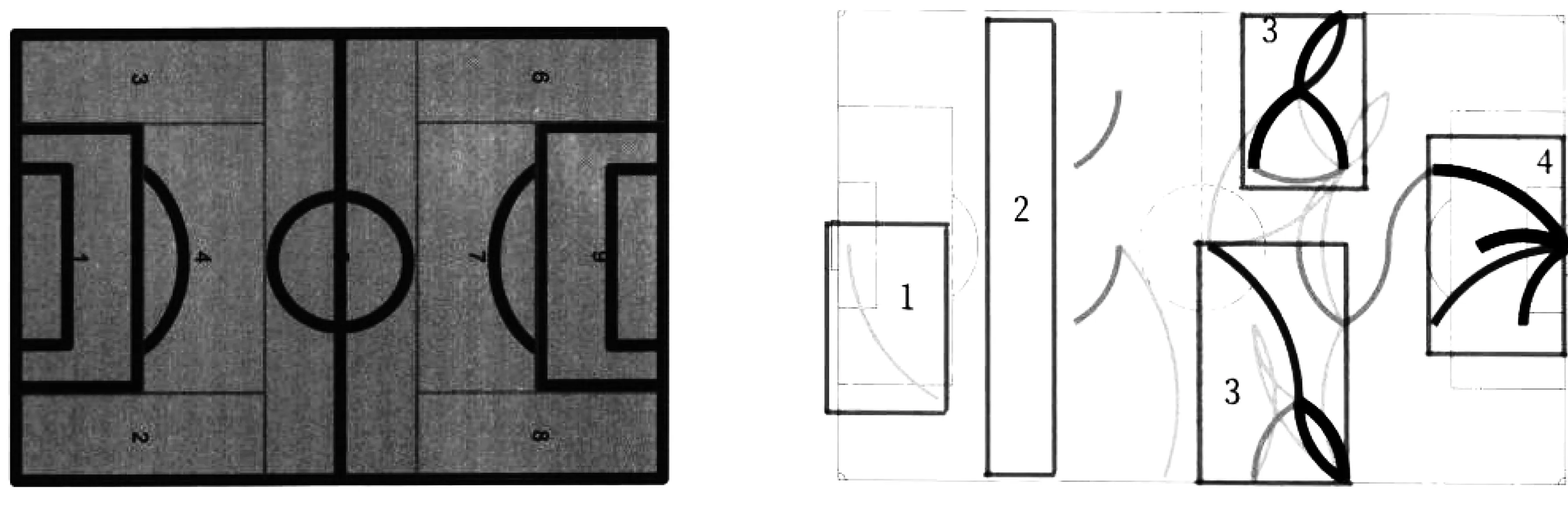
图2 球场划分图 图3 2014年FIFA世界杯半决赛，阿根廷队的传球网络

图3中1号框表示守门员以短传为主，2号框表示1/3半场区域传球较少，3号框表示边路往中路渗透，4号框代表威胁进攻.图3所示的图，不同颜色框内的传球网络形成图论中的子图，边的粗细代表传球次数多少，其蕴含着图论中平行边和度数的概念.子图是图的一部分，即子图的顶点集合和边集都是整个图的子集.

2.3 球场-球员传球网络——图的顶点坐标

球场-球员传球网络[11]结合前面两种网络的特性，既关心发生传球事件的区域，又关心是谁传了球.将球场划分成9个区域(图2)，以球场中不同区域的不同球员作为网络节点，形成一个球场—球员传球网络见图4.

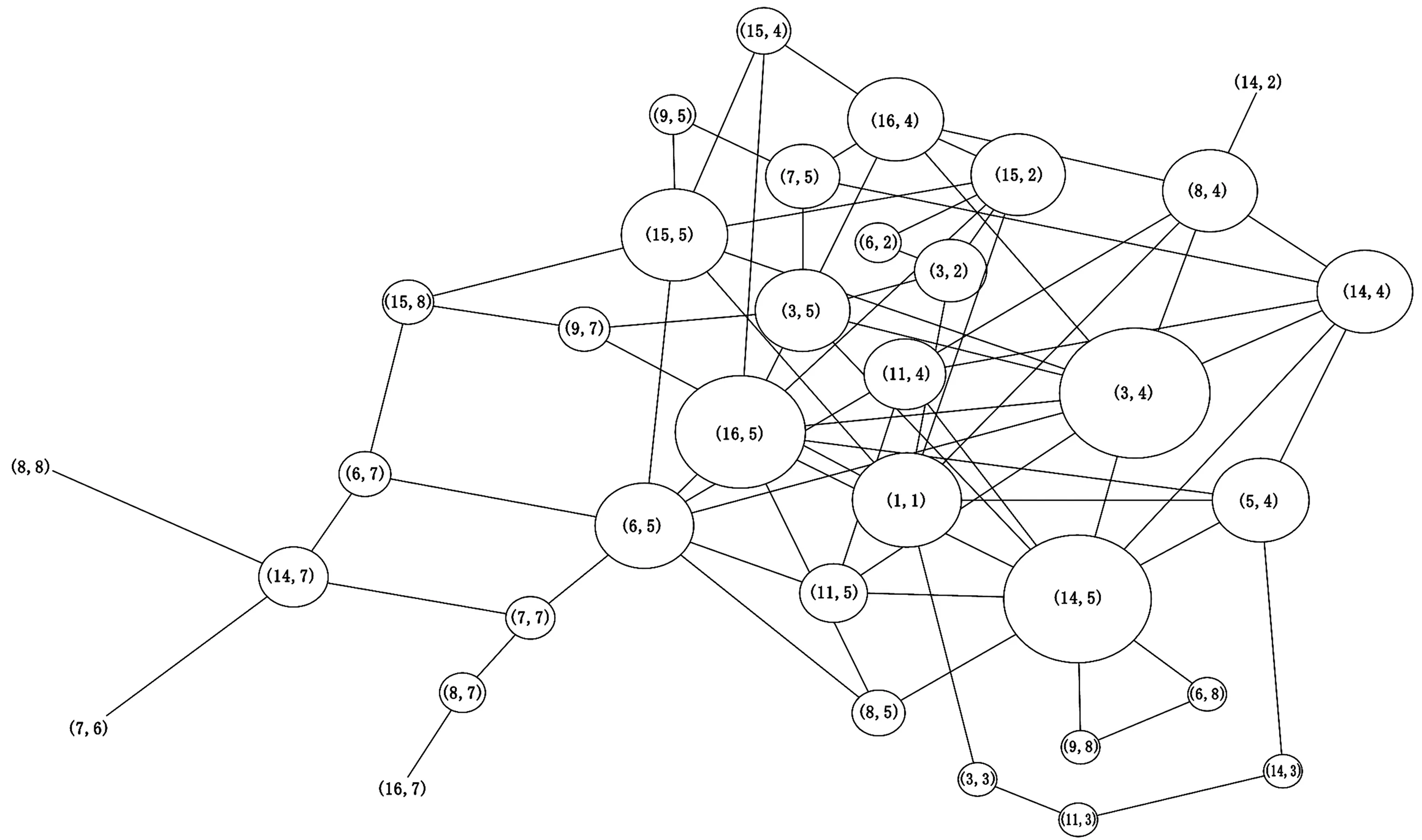
图4 2010年FIFA世界杯比赛中，西班牙球队的传球网络

球场—球员传球网络中的网络节点由二维坐标(p，z)表示，其中p为球员编号，z为球场区域编号，比如顶点(16， 5)代表16号球员在区域5产生一次传球.因此基于球场-球员传球网络形成的图，其图顶点都由二维坐标表示，这种表示既拓宽了学生对图顶点的理解——顶点不仅可以代表一件事物，还可以代表一个二维信息甚至多维信息，又为学生理解和分析传球网络奠定了基础.

3 图的矩阵表示与足球网络相融合

图可以用集合来定义，但多半用图形来表示，还可以用矩阵来表示.用矩阵来表示图有利于用代数方法去研究图的性质，同时也为计算机存储和处理图的信息提供便利.因此，图的矩阵表示具有重要意义.为了用矩阵表示图，必须指定顶点或边的顺序，即对图进行标定.本小节主要讨论如何将有向图的关联矩阵、邻接矩阵和可达矩阵与足球网络相融合.

基于图5所示的传球网络形成的图，其顶点为足球球员的名字，有向边表示球员之间的传球关系.为方便起见，再用矩阵表示的时候只选取图5中有黑色网络连线和对应的网络节点形成的图，对顶点和边进行标定见图6，其中图6是图5的子图.

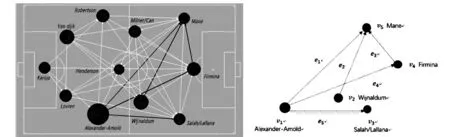
图5 2018年欧洲冠军联赛中Liverpool球队的部分传球网络 图6

3.1 关联矩阵

有向图的关联矩阵中，顶点作为边的起点记为1，终点记为-1，如果顶点和边不关联，则记为0，其描述顶点和边的关系.因此，图6对应的关联矩阵M为

根据关联矩阵的性质可以对传球网络做如下解释：

(a) 关联矩阵M中每一列恰好有一个+1和一个-1，可以理解为图6所示的传球网络中每发生一次传球必有一个发球者(+1)和一个接球者(-1)；

(b) 关联矩阵M中-1的个数等于+1的个数，都等于边的条数(握手定理)，可以理解为图6所示的传球网络中总体的发球数等于接球数，都等于发生传球的次数；

(c) 关联矩阵M中第i行，+1的个数等于vi的出度，-1的个数等于vi的入度.例如关联矩阵M中第四行一个+1，一个-1，意味着图6所示的传球网络中球员v4Firmina分别有一次发球和一次接球.

3.2 邻接矩阵

有向图的邻接矩阵，其矩阵元素aij为顶点vi邻接到顶点vj的边数，其描述顶点和顶点之间的邻接关系.因此，图6对应的邻接矩阵A为

根据邻接矩阵的性质对传球网络可以做如下解释：

(a) 对邻接矩阵的某一行元素相加等于对应顶点的出度.例如邻接矩阵A中第一行元素之和为3，意味着图6所示的传球网络中球员v1Alexander-Amold发球3次；

(b) 邻接矩阵的某一列元素之和等于对应顶点的入度.例如邻接矩阵A中第五列元素之和为3，意味着图6所示的传球网络中球员v5Mane接球3次；

3.3 可达矩阵

有向图的可达矩阵P，其矩阵元素pij为0或1，如果vi可达vj则记为1，可达意味着vi到vj有路径，否则记为0，并且认为vi是可达vi本身的，即顶点到自身是可达的.可达矩阵描述的是图的连通性强弱.图6对应的可达矩阵P为

如果可达矩阵元素全为1，则该图为强连通图.图6对应的可达矩阵P，其元素并不全为1，说明了图6所示的传球网络中五个球员之间并没有完全达到或者间接达到相互传球.所谓间接可以根据图6理解为球员v2Wijnaldum没有直接或者间接传球给球员v4Firmina.

4 教学效果

为了了解图论与传球网络相融合的教学实践的教学效果，设计了一份学生对该教学效果的问卷调查.由于该教学实践是在我校首次进行，所以只针对我校参与这次教学实践的2019级智能体育、数据科学与大数据技术两个专业学生，通过雨课堂发放教学效果的调查问卷，共计59名学生参加了问卷调查，其中收回有效问卷57份，无效问卷1份，作废问卷1份，具体参与人数反馈情况如图7.

图7 问卷收集情况

表1 调查问卷的统计结果

从上表中可以看出，在图论教学之前，有57%的学生已经对足球网络有了不同程度的了解，由于我校属于体育院校，得益于学校的文化氛围和办学理念，这个初始数据还是比较高的，经过交叉学科教学实践该项数据提升到86%，有了较大提升.在教学过程中，加入足球网络内容显著提升了学生学习的兴趣，课堂表现良好.在教学实践产生的效果方面，可以看出有84%的学生觉得图论在足球网络分析中有重要作用，89%的学生对体育开发、科技产生了兴趣，对整体课堂效果的满意度达到了98%. 总之，将图论教学与传球网络相融合的教学实践不仅体现交叉学科教学理念，更重要地是提升了学习兴趣，丰富了课堂氛围，开拓了学生的视野特别体育科技的视野，加强了学生对本专业的进一步认识和体会，激发了学生对体育开发、科技的热情和向往.

5 结 论

本文主要介绍了图论这个知识模块的教学实践与探究，教学过程中将图论与体育领域的传球网络相融合，推动了交叉学科的教学理念，贯穿了科技服务体育的思想，同时积极响应了习近平总书记“少年强，中国强，体育强，中国强”的号召.我国体育事业蓬勃发展，特别是三大球的发展，受到国民的关注度越来越高，然而我国这些团体运动项目的表现和人们的期待之间仍然存在较大差异，为了缩小这个差距，需要研究团体运动项目的比赛表现，而传球网络就是一个重要分析工具.本文的教学实践将图论与传球网络相融合，希望学生认识到通过现在所学的图论初步知识和后续深化学习，能够很好应用到对传球网络的科学分析，进一步为体育职能部门和教练团队进行个性化训练方案开发、专业精英运动员培养和比赛技战术策略制定等做出贡献，用实际行动服务于中国体育.因此，将传球网络融入到图论的教学实践中，不仅可以增强课堂的趣味性，也可以让学生了解所学的理论课程在体育开发和科技中具有不可替代的地位，实现学以致用的目标.

致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.