n阶圈图的一些代数性质
2016-11-29莫贵圈
莫贵圈
(贵州师范学院 数学与计算机科学学院,贵州 贵阳 550018)
n阶圈图的一些代数性质
莫贵圈
(贵州师范学院 数学与计算机科学学院,贵州 贵阳 550018)

圈图;关联矩阵;邻接矩阵;行列式;秩
1 引言及相关概念
图论是数学的一个分支,它以图为研究对象,是研究结点和边组成的图形的数学理论和方法.图的表示方式通常有三种,可以用集合、图形和矩阵来表示.用矩阵表示图便于用代数方法来研究图的性质,也便于用计算机来处理图.常用的图的矩阵表示有: 关联矩阵、邻接矩阵和可达矩阵.图的关联矩阵用来表示各个结点和每条边之间的关系,它是描述一个图中结点与边关联性质的矩阵;图的邻接矩阵用来表示各个结点之间的关系,它是描述一个图中结点与结点是否相关的矩阵.目前,已有不少学者对图的关联矩阵、邻接矩阵进行了研究,例如文献[1]研究了应用代数学中的置换理论,得出了关联矩阵的一些特殊性质.关联矩阵、邻接矩阵都是特殊的(0,1)矩阵,文献[2]研究了线和为2的两种(0,1)矩阵的秩.文献[3]介绍了一种新方法,该方法建立属性的关联矩阵,然后通过计算属性的类方差选择分裂属性,对原来的ID3算法加以改进.
关联矩阵和邻接矩阵的应用,是学者们讨论的热点之一.例如文献[4]讨论了在带权图中利用邻接矩阵求最短通路;文献[5]介绍了在二部图定义的基础上,给出了一种基于邻接矩阵的新判断算法,该算法能较好解决二部图的判定问题[6];研究了利用图的邻接矩阵及关联矩阵求简单图的最大匹配和二分图的完美匹配;文献[7]研究了利用邻接矩阵和关联矩阵来判断无向图同构的方法;文献[8]介绍了在图的关联矩阵基础上,提出了求无权简单图最大匹配的一种操作简单、编程容易的新算法——“表单作业法”;文献[9]介绍了邻接矩阵与关联矩阵在图论问题中的一些应用,解决了最大匹配、最小顶点覆盖、选址等问题.综上可见,学者们对有向图和无向图的关联矩阵、邻接矩阵的代数性质的研究甚少,因此,本文将重点研究n阶无向圈图的关联矩阵和n 阶有向圈图的关联矩阵、邻接矩阵的行列式、秩等代数性质.
定义1[10](1)设G=
(2)设D
定义2[10]设无向图G=
定义3[10]设有向无环图G=
则称(mij)n×m为G的关联矩阵,记作M(G).

2 结论及其证明
定理1 设Cn是n(n≥3)阶无向圈图,Cn的关联矩阵M(Cn)的行列式与秩分别为:
证明 因为Cn是n阶无向圈图, 所以Cn的关联矩阵为:




综上得n C 的关联矩阵M(Cn)的行列式与秩分别为:
定理2 n阶有向圈图的关联矩阵M(Cn)的行列式与秩分别为:



所以∀n∈N,都有|M(Cn)|=0.

定理3 n阶有向圈图的邻接矩阵A(Cn)的行列式与秩分别为:
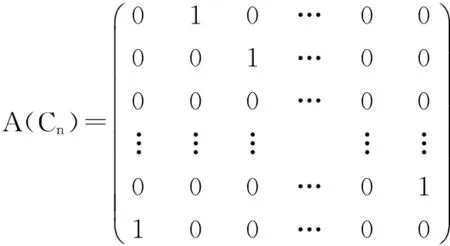
由上述讨论知|A(Cn)|≠0知, A(Cn)为满秩矩阵,即R(A(Cn))=n.综上得,n阶有向圈图的邻接矩阵A(Cn)的行列式与秩分别为:
[1] 董永红,简芳洪.关联矩阵的一些特殊性质[J].九江学院学报(自然科学版),2011,44(3):37-39.
[2] 朱雪芳.一类(0,1)矩阵的秩[J].杭州师范大学学报(自然科学版),2013,12(3):223-226.
[3] 方立.基于关联矩阵的决策树分类算法[J].长春大学学报,2013,23(4):426-429.
[4] 黄师化. 邻接矩阵求带权图中最短通路[J].安庆师范学院学报(自然科学版),2013,19(4):26-28.
[5] 王敏,韩俊英.一种基于邻接矩阵的二部图判定算法[J].重庆理工大学学报(自然科学版),2011,25(8):75-77.
[6] 李世群.简单图的最大匹配的矩阵求法[J].数学的实践与认识,2007,37(7):120-124.
[7] 张磊,李世群.用矩阵判断无向图同构的几种方法[J].衡阳师范学院学报,2011,32(6):19-21.
[8] 段春生,庄刘.关于简单图最大匹配的矩阵算法研究[J].四川师范大学学报(自然科学版),2012,35(4):478-481.
[9] 付小娟,李宗涛. 基于邻接矩阵与关联矩阵解决最大匹配等问题[J].贵阳学院学报(自然科学版),2015,10(2):7-9.
[10] 屈婉玲,耿素云.离散数学[M].3版.北京:清华大学出版社,2014:171-172.
责任编辑:时 凌
SomeAlgebraicPropertiesofnOrderCircleGraphs
MOGuiquan
(CollegeofMathematicsandComputerScience,GuizhouEducationUniversity,Guiyang550018,China)
Inthispaper,wediscussthecorrelationmatrixofnorderundirectedgraphandthecorrelationmatrixoforderdirectedgraph,thedeterminantofadjacencymatrix,thealgebraicpropertiesofrankandsoon,andgetthecorrespondingconclusion:①thedeterminantandrankofthecorrelationmatrixM(Cn)ofnorderundirectedgraphsare:|M(Cn)|=2,R(M(Cn))=n,nisodd;|M(Cn)|=0,R(M(Cn))=n-1, niseven.②ThedeterminantandrankofthecorrelationmatrixM(Cn)ofnorderdirectedgraphare:|M(Cn)|=0,R(M(Cn))=n-1,nisinteger. ③ThedeterminantandrankoftheadjacencymatrixA(Cn)ofthedirectedgraphare:|A(Cn)|=1,R(A(Cn)=n,nisodd; |A(Cn)|=-1,R(A(Cn))=n,niseven.
circlegraph;incidencematrix;adjacencymatrix;determinant;rank
2016-08-12.
国家自然科学基金项目(11661023);2015年省级本科教学工程建设项目(黔教高发[2015]337号).
莫贵圈(1984- ),女,硕士生,讲师,主要从事半群的研究.
1008-8423(2016)03-0295-04
10.13501/j.cnki.42-1569/n.2016.09.013
O
A
