基于关联矩阵主对角线谱理论的欧拉图研究

赵 凯, 王晓平,董大伟

(1.宜宾职业技术学院现代制造工程系，四川宜宾 644003；2.宜宾职业技术学院人文社科系，四川宜宾 644003； 3.西南交通大学牵引动力国家重点实验室，四川成都 610031)

基于关联矩阵主对角线谱理论的欧拉图研究

赵 凯1, 王晓平2,董大伟3

(1.宜宾职业技术学院现代制造工程系，四川宜宾 644003；2.宜宾职业技术学院人文社科系，四川宜宾 644003； 3.西南交通大学牵引动力国家重点实验室，四川成都 610031)

本文利用图的顶点与边邻接矩阵建立并定义了顶点关联矩阵和边关联矩阵，以及顶点关联矩阵和边关联矩阵的主对角线谱概念，并给出了利用关联矩阵主对角线谱判定欧拉图问题的方法。

图论；关联矩阵；主对角线谱；哥尼斯堡七桥问题

目前，矩阵和图论理论中对关联矩阵和邻接矩阵关系的研究较少[1].徐俊明[2]研究了关联矩阵和邻接矩阵的行列式问题，但没有对关联矩阵和邻接矩阵之间的关系进行关联.Jonathan L Gross and Jay Yellen[3]构造的顶点关联矩阵和边关联矩阵的对角线的值均为零，而J A Bondy[4]将各个顶点度引入到关联矩阵中，但顶点关联是人为设定的，对原始图来讲存在部分的信息遗失.本文引入主对角线谱建立顶点关联矩阵和边关联矩阵之间的关系，并讨论了关联矩阵及主对角线谱的基本性质，最后应用顶点关联矩阵的主对角线谱进行欧拉图的判定.

1 邻接矩阵的定义

定义2 矩阵V(G)=(vij)m×m称为图G的顶点关联矩阵，其中V(G)=K(G)KT(G).

定义3 矩阵E(G)=(eij)n×n称为图G的边关联矩阵，其中E(G)=KT(G)K(G).

显然，V(G)和E(G)都是对称矩阵.

性质2 对于边关联矩阵E(G)=(eij)n×n，当eii=0时矩阵变成图论中的关联矩阵.

性质3 顶点关联矩阵V(G)和边关联矩阵E(G)的迹相等，即tr(V)=tr(E).

定义4Diag-SpecV(G)称为图G的顶点关联矩阵V(G)的主对角线谱，令

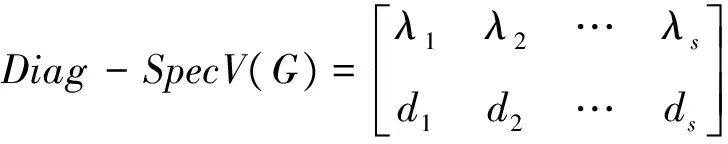
(1)

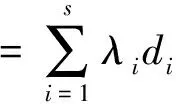
在图论中，迹可用于统计图中各顶点的度数和.

2 关联矩阵用于欧拉图的判断实例

例1 判定哥尼斯堡七桥问题(图1)是否为欧拉图.

该问题的连通示意图G(图2)共有A、B、C、D四个顶点和标号从1到7的七条边.此问题曾经是世界著名的数学难题，最终由数学家欧拉通过图论办法得以解决，其结论是无法只从每个桥通过一次走遍七座桥.实际上，可以通过建立其关联矩阵的主对角线谱来判断该难题是否成立.这一计算和判定方法易于以计算机算法的形式实现，也是对此类图论判定问题的很好的自动判定方法.

图1 哥尼斯堡七桥问题

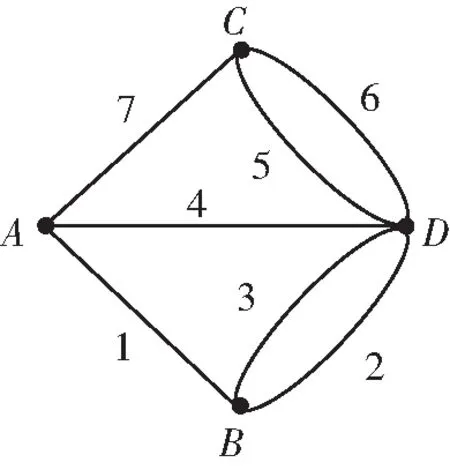
图2 哥尼斯堡七桥问题的连通示意图

首先，建立图的顶点与边邻接矩阵K(G)，进而推算顶点关联矩阵V(G)=K(G)KT(G)和边关联矩阵E(G)=KT(G)K(G).

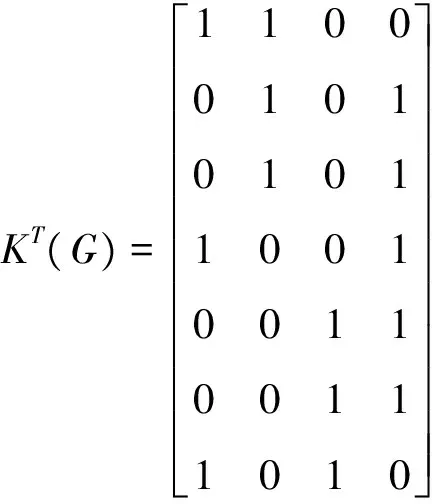
例2 判定图3是否为欧拉图.

例3 判定图4是否为欧拉图.

图3 一种欧拉图的连通图

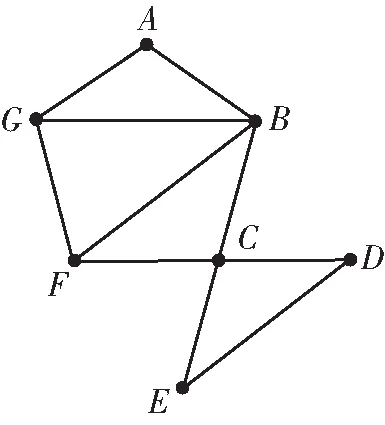
图4 一种半欧拉图的连通图

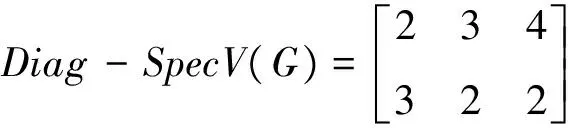
由上述实例说明，利用顶点关联矩阵对角线谱的计算和统计，可以有效地判定连通图是否为欧拉图，并判断欧拉图的类型.

实际上，从前面的推算过程可以看出，邻接矩阵K(G)与关联的V(G)和E(G)是互通的，只要知其一，其余两个就可推算出来.一般而言，连通图的顶点数量都比边的数量少，所以常用顶点关联矩阵表示图，而另外两个矩阵由顶点关联矩阵推出.又因为顶点关联矩阵是对称矩阵，由性质1可知，主对角线上的单元数据可以通过邻接矩阵的行或列推导出来，因此，实际需要计算机储存的数据量是m(m-1)/2.可见，使用图的顶点关联矩阵可以用较少的数据存储相同大小信息量的图。

3 通过主对角线谱法判定欧拉图的方法

已为人们熟知的欧拉一笔画的判据是：(1)欧拉图是可以一笔画成的，它是由偶点组成的连通图.一笔画时，可以从任一偶点开始，最后以这个点为终点画完得到欧拉闭迹.(2)半欧拉图是可以一笔画成的，它是只有两个奇点的连通图(其余都为偶点).一笔画时，必须把一个奇点作为起点，另一个奇点作为终点.(3)其他情况的图都不能一笔画出.

4 结语

通过顶点与边邻接矩阵可以推导出顶点关联矩阵和边关联矩阵，定义方阵的主对角线谱，阐明主对角线谱和矩阵迹在图论中的意义.通过本文所引入的矩阵主对角线谱可以方便地自动判定连通图的欧拉性质，所引入的关联矩阵和邻接矩阵在图论以外的机构学[5]等其他学科中有很大的应用意义.

[1]张先迪,李正良.图论及其应用[M].北京:高等教育出版社,2005:15-16.

[2]徐俊明.图论及其应用[M].3版,合肥:中国科学技术大学出版社,2014:91-93.

[3] Jonathan L Gross,Jay Yellen.Handbook of graph theory[C].CRC Press Taylor & Francis Group,2014:12.

[4]J A Bondy,U S R Murty.Graph theory[M].Springer,2008:6.

[5]Z Kai.Planar mechanism incidence matrices and main diagonal spectrum[C].International Workshop on Materials Engineering and Computer Sciences,2015.

Euler Graph Research Based on Main Diagonal Spectrum Theory of Incidence Matrix

ZHAO Kai1，WANG Xiao-ping2，DONG Da-wei3

(1.Modern Manufacturing Engineering Department of Yibin Vocational and Technical College, Yibin Sichuan 644003,China； 2.Humanities and Social Science Department of Yibin Vocational and Technical College,Yibin Sichuan 644003,China； 3.Traction Power State Key Laboratory of SouthWest Jiaotong University,Chengdu Sichuan 610031,China)

By using the incidence matrix of vertex-edge and the main diagonal spectrum of the correlated matrix, the vertex incidence matrix and edge incidence matrix were established. Then, the main diagonal spectrum of the correlated matrix was used to prove or judge Euler graph problem.

graph theory; incidence matrix; main diagonal spectrum; Knigsberg bridges problem

2017-03-03

赵 凯(1972- )，男，副教授，硕士，从事机构学、图论及机械电子工程研究。

O151.22

A

2095-7602(2017)08-0010-04