两类剖分图的边理想的正则度

朱广俊， 张伽祺

(苏州大学 数学科学学院，江苏 苏州215006)

1 引 言

图论中，完全二部图和剖分图是性质比较好的常见的两类图，很多学者已从组合的角度对它们进行了研究，见参考文献[1-3].由于超图的边和单项式理想的生成元之间可以一一对应，而单项式理想又是多项式环中一类非常重要的理想，通过这种对应关系，超图的组合性质与单项式理想的代数性质之间有着密切的联系.本文主要研究完全二部图和两类m-剖分图的边理想的代数性质与组合性质之间的关系，通过构造合适的短正合列，并利用线图、圈图和单项式理想的正则度的公式，给出两类m-剖分图的边理想的正则度的精确公式，这些公式推广了m个顶点的线图和圈图的正则度公式.从而加深对多项式环中单项式理想的一些性质的理解.

2 用到的定义和引理

约定设m为一个实数， 约定

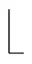
m

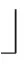
表示不超过m的最大整数.

定义1[4]设G=(V，E)为一个图， 它的顶点集和边集分别为V和E， 其中E中的元素{u，v}是以u，v为端点的边. 称不含环(两个端点相同的一条边)和重边(以两个顶点为端点的多条边)的图为简单图.

定义2[4]设G=(V(G)，E(G))和H=(V(H)，E(H))为两个简单图，若V(H)⊂V(G)，E(H)⊂E(G)，且x，y∈V(H)，则边{x，y}∈E(H)的充要条件是边{x，y}∈E(G).则称H为G的诱导子图.

定义4[5]设G=(V，E)为一个简单图，其中V={x1，…，xn}.设S=k[x1，…，xn]为域k上n个变量的多项式环，定义G的边理想为

I(G)=(xixj|{xi，xj}∈E).

定义5[5]设S=k[x1，…，xn]是域k上n个变量的多项式环，M为一个有限生成的分次S-模.设

0→⊕jS(-j)βp，j(M)→⊕jS(-j)βp-1，j(M)→…→⊕jS(-j)β0，j(M)→M→0

为M的一个极小分次自由预解，其中S(-j)i=Si-j，这里Si-j是多项式环S的第(i-j)个分次部分，βi，j(M)称为模M的第(i，j)-分次Betti数，它等于M的第i个合冲模的极小生成元集中次数为j的元素的个数，是模M的一个代数不变量.称

reg(M)∶=max{j-i|βi，j(M)≠0}

为M的正则度.它刻画了M的极小分次自由预解中的合冲模的复杂程度.

引理1[5]设S=k[x1，…，xn]是域k上n个变量的多项式环，I⊂S为一个真的齐次理想，则

引理2[6-7]设T1=k[x1，…，xm]，T2=k[y1，…，yn]是域k上的两个多项式环，I⊂T1，J⊂T2为两个非零的齐次真理想，{x1，…，xm}∩{y1，…，yn}=∅，设T=k[x1，…，xm，y1，…，yn]，则

(i)reg(I+J)=reg(I)+reg(J)-1；

(ii)reg(IJ)=reg(I)+reg(J).

引理3[6，8]设n≥2为一个整数，Ln是一个n个顶点的线图，I(Ln)为Ln的边理想，则

reg(I(Ln))=n+13+1.

引理4[6，8]设n≥3为一个整数，Cn是一个n个顶点的圈图，I(Cn)为Cn的边理想，则

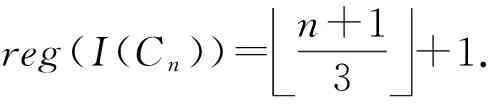
reg(I(Cn))=n+13+1.

引理5[7]设u1，…，ur为S中的齐次正则序列，且deg(u1)=…=deg(ur)=d;设I=(u1，…，ur)，则对任意的正整数m，有

reg(Im)=dm+(d-1)(r-1).

引理6[7，9]设0→M→N→P→0为一个有限生成的分次S-模短正合列， 则

reg(N)≤max{reg(M)，reg(P)}，

当reg(P)≠reg(M)-1时，等号成立.

3 主要结果

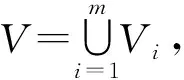
证设Vi={xi1，…，xiqi}，其中i=1，…，3.

① 当m=2时，则G的边理想为

I(G)=(x11x21，x11x22，…，x11x2q2，x12x21，x12x22，…，x12x2q2，…，x1q1x21，x1q1x22，…，x1q1x2q2)

=(x11，x12，…，x1q1)(x21，x22，…，x2q2)=JK.

其中J=(x11，x12，…，x1q1)，K=(x21，x22，…，x2q2).从而I(G)t=JtKt.由引理2(ii)和引理5，可得

reg(I(G)t)=reg(JtKt)=reg(Jt)+reg(Kt)=t+t=2t，

其中S1=k[x11，…，x1q1]，S2=k[x21，…，x2q2].

② 当m=3 时，则G的边理想为

I(G)=(x11x21，x11x22，…，x11x2q2，x12x21，x12x22，…，x12x2q2，…，x1q1x21，x1q1x22，…，x1q1x2q2)

+(x21x31，x21x32，…，x21x3q3，x22x31，x22x32，…，x22x3q3，…，x2q2x31，x2q2x32，…，x2q2x3q3)

=(x11，x12，…，x1q1，x31，x32，…，x3q3)(x21，x22，…，x2q2)=JK.

其中J=(x11，x12，…，x1q1，x31，x32，…，x3q3)，K=(x21，x22，…，x2q2).从而I(G)t=JtKt.由引理2(ii)和引理5，可得

reg(I(G)t)=reg(JtKt)=reg(Jt)+reg(Kt)=t+t=2t，

其中S1=k[x11，x12，…，x1q1，x31，x32，…，x3q3]，S2=k[x21，…，x2q2].

reg(I(G))=m+13+1.

证当m=2，3时，由定理1可知，结论成立.设m≥4，且结论对所有小于m的整数都成立.此时记G的边理想I(G)为I，则

I=(x11x21，x11x22，…，x11x2q2，x12x21，x12x22，…，x12x2q2，…，x1q1x21，x1q1x22，…，x1q1x2q2)

+(x21x31，x21x32，…，x21x3q3，x22x31，x22x32，…，x22x3q3，…，x2q2x31，x2q2x32，…，x2q2x3q3)+…

+(xm-1，1xm1，…，xm-1，1xmqm，xm-1，2xm1，…，xm-1，2xmqm，…，xm-1，qm-1xm1，…，xm-1，qm-1xmqm).

设J=(x21，x22，…，x2q2，x41，x42，…，x4q4)，则当m=4，5时，有I∶x31=J;

当m≥6时，有

I∶x31=J+(x51x61，…，x51x6q6，x61x71，…，x61x7q7，…，xm-1，qm-1xm1，…，xm-1，qm-1xmqm).

从而由引理2(i)和归纳假设，可得

当m=4，5时，有

reg(I∶x31)+1=1+1=2;

(1)

当m≥6时，有

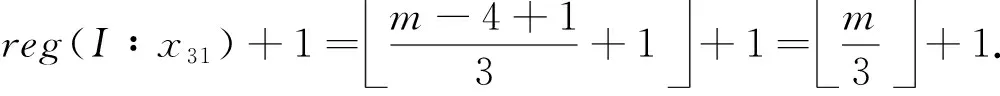
reg(I∶x31)+1=m-4+13+1+1=m3+1.

(2)

对任意1≤i≤q3-1，有

(I，x31，…，x3i)=(x31，…，x3i)+(x21x3，i+1，…，x21x3q3，…，x2q2x3，i+1，…，x2q2x3q3)

+(x3，i+1x41，…，x3，i+1x4q4，x3，i+2x41，…，x3，i+2x4q4，…，x3q3x41，…，x3q3x4q4)

+(x41x51，x41x52，…，x41x5q5，…，xm-1，qm-1xm1，xm-1，qm-1xm2，…，xm-1，qm-1xmqm).

设Ki=J+(x31，…，x3i)，则

当m=4，5时，有((I，x31，…，x3i)∶x3，i+1)=Ki;

当m≥6时，有

((I，x31，…，x3i)∶x3，i+1)=Ki+(x51x61，x51x62，…，x51x6q6，…，xm-1，qm-1xm1，…，xm-1，qm-1xmqm).

由引理2(i)和归纳假设，可得

当m=4，5时，有

reg((I,x31,…,x3i)∶x3,i+1)+1=1+1=m3+1;

(3)

当m≥6时，有

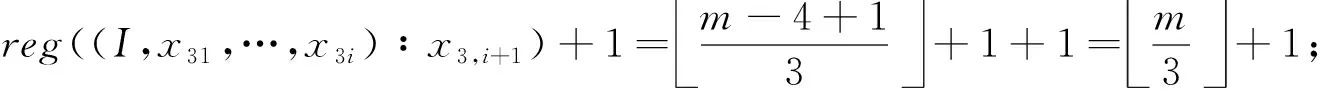
reg((I,x31,…,x3i)∶x3,i+1)+1=m-4+13+1+1=m3+1;

(4)

设L=(x31，…，x3q3)+(x11x21，…，x11x2q2，…，x1q1x21，…，x1q1x2q2)，则

当m=4时，有(I，x31，…，x3q3)=L;

当m≥5时，有

(I，x31，…，x3q3)=L+(x41x51，x41x52，…，x41x5q5，…，xm-1，qm-1xm1，…，xm-1，qm-1xmqm).

由引理2(i)和归纳假设，可得

当m=4时，有

reg((I,x31,…,x3q3))=2+13+1=53+1;

(5)

当m≥5时，有

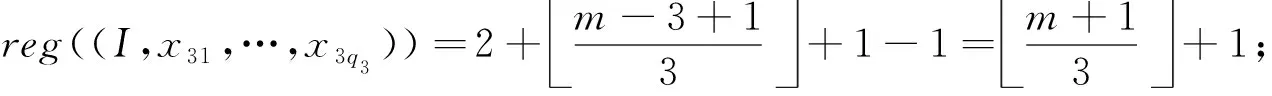
reg((I,x31,…,x3q3))=2+m-3+13+1-1=m+13+1;

(6)

将公式(1)-(6)和引理6运用到下列短正合列

可得

reg(I)=m+13+1.

说明1 定理2中的m-剖分图的正则度公式推广了m个顶点的线图的正则度公式.

reg(I(G))=m+13+1.

证设图G的边理想I(G)为I，则

I=(x11x21，x11x22，…，x11x2q2，x12x21，x12x22，…，x12x2q2，…，x1q1x21，x1q1x22，…，x1q1x2q2)

+(x21x31，x21x32，…，x21x3q3，x22x31，x22x32，…，x22x3q3，…，x2q2x31，x2q2x32，…，x2q2x3q3)

+…+(xm-1，1xm1，…，xm-1，1xmqm，xm-1，2xm1，…，xm-1，2xmqm，…，xm-1，qm-1xm1，…，xm-1，qm-1xmqm)

+(xm1x11，…，xm1x1q1，xm2x11，…，xm2x1q1，…，xmqmx11，…，xmqmx1q1).

设集合V1，…，Vm中元素个数大于1的集合的个数为k，我们对k进行归纳.

当k=0时，由引理4，结论成立.

当k=1时，不妨设|V1|≥2，从而图G的边理想为

I=(x11x21，x12x21，…，x1q1x21，x21x31，x31x41，…，xm-1，1xm1，xm1x11，…，xm1x1q1).

设J=(x21，xm1)，则

当m=3，4时，有I∶x11=J;

当m≥5时，有I∶x11=J+(x31x41，x41x51…，xm-2，1xm-1，1).

从而当m=3，4时，有

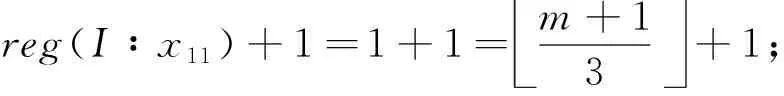
reg(I∶x11)+1=1+1=m+13+1;

(7)

当m≥5时，由引理3可知

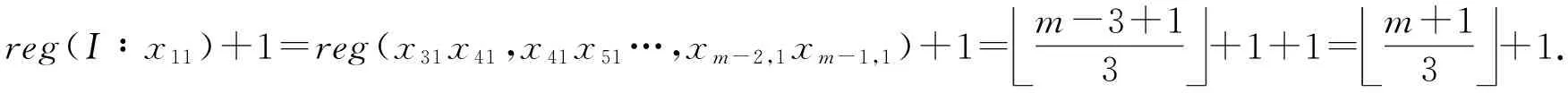
reg(I∶x11)+1=reg(x31x41,x41x51…,xm-2,1xm-1,1)+1=m-3+13+1+1=m+13+1.

(8)

对任意1≤i≤q1-2，设Ji=(x11，…，x1i，x21，xm1)，K=(x31x41，…，xm-2，1xm-1，1).则

当m=3，4时，有(I，x11，…，x1i)∶x1，i+1=Ji;

当m≥5时，有(I，x11，…，x1i)∶x1，i+1=Ji+K.

从而当m=3，4时，有

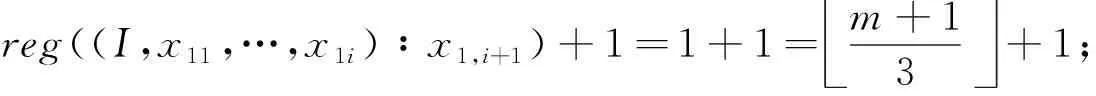
reg((I,x11,…,x1i)∶x1,i+1)+1=1+1=m+13+1;

(9)

当m≥5时，由引理2(i)和引理3可知

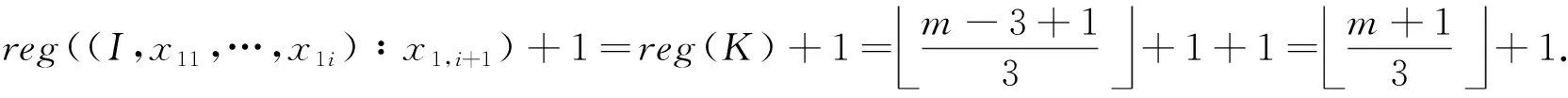
reg((I,x11,…,x1i)∶x1,i+1)+1=reg(K)+1=m-3+13+1+1=m+13+1.

(10)

又

(I，x11，…，x1，q1-1)=(x11，…，x1，q1-1，x1q1x21，x21x31，…，xm-1，1xm1，xm1x1q1).

从而由引理2(i)和引理4得

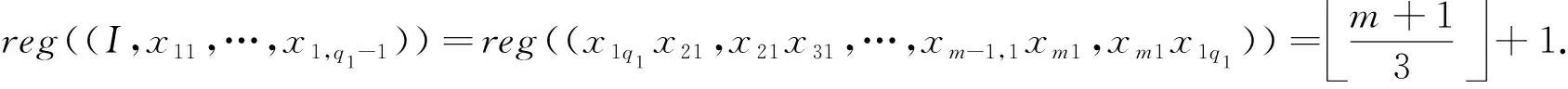
reg((I,x11,…,x1,q1-1))=reg((x1q1x21,x21x31,…,xm-1,1xm1,xm1x1q1))=m+13+1.

(11)

将公式(7)-(11)和引理6运用到下列短正合列

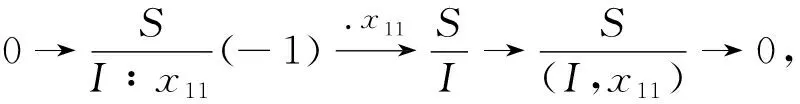
可得

reg(I)=m+13+1.

当k>1时，取一个元素个数大于1的集合，不妨为V1.设L=(x21，…，x2q2，xm1，…，xmqm)，

M=(x31x41，…，x31x4q4，x32x41，…，xm-2，1xm-1，1，…，xm-2，qm-2xm-1，1，…，xm-2，qm-2xm-1，qm-1).

则当m=3，4时，有I∶x11=L; 当m≥5时，有I∶x11=L+M.

从而当m=3，4时，有

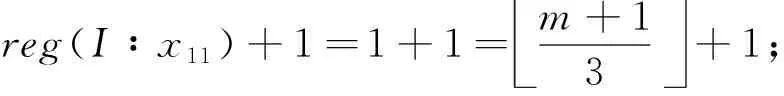
reg(I∶x11)+1=1+1=m+13+1;

(12)

当m≥5时，由定理2可知

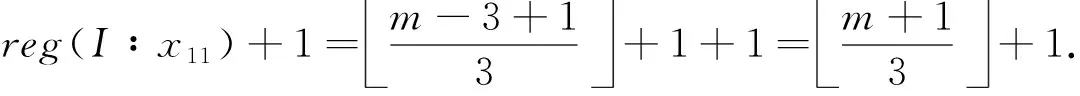
reg(I∶x11)+1=m-3+13+1+1=m+13+1.

(13)

对任意1≤i≤q1-2，设Ni=(x11，…，x1i，x21，…，x2q2，xm1，…，xmqm).则

当m=3，4时，有(I，x11，…，x1i)∶x1，i+1=Ni; 当m≥5时，有(I，x11，…，x1i)∶x1，i+1=Ni+M.从而当m=3，4时，有

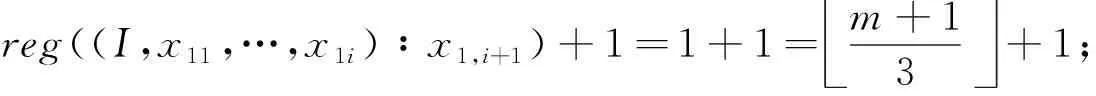
reg((I,x11,…,x1i)∶x1,i+1)+1=1+1=m+13+1;

(14)

当m≥5时，由定理2可知

reg((I,x11,…,x1i)∶x1,i+1)+1=m-3+13+1+1=m+13+1.

(15)

注意(I，x11，…，x1，q1-1)=(I(G{x11，…，x1，q1-1})，x11，…，x1，q1-1)，其中G{x11，…，x1，q1-1}是G去掉了V1中的点x1q1，…，x1q1-1以及与这些点相连的边后得到的图，从而G{x11，…，x1，q1-1}的顶点的部集V1{x11，…，x1，q1-1}，…，Vm中元素个数大于1的集合的个数为k-1，从而由归纳假设可得

(16)

将公式(12)-(16)和引理6运用到下面的短正合列

…………

可得

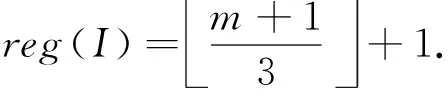
reg(I)=m+13+1.

说明2 定理3中的m-剖分图的正则度公式推广了m个顶点的圈图的正则度公式.

4 结 论

本文主要利用线图、圈图和单项式理想的正则度的公式，并通过构造合适的短正合列，给出了两类m-剖分图的边理想的正则度的精确公式，它们分别推广了线图、圈图的正则度公式.本文的工作为简单图的代数性质的研究提供了有益的探索，加深了同学们对相关理论和技能的理解和掌握.

致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.