基于Minitab软件的低内应力镍电铸工艺优化*

同济大学机械与能源工程学院 王昆 汪聿标

为消除阴极和阳极形状和尺寸参数对沉积层内应力的影响，本文以铜薄片为阴极、镍板为阳极进行了响应曲面设计试验。采用Minitab进行试验设计与分析得到镍电铸基本工艺参数：电流密度、氨基磺酸镍浓度、电铸液温度与内应力的回归方程。基于响应面建立的模型进行优化求解，并通过试验验证，得到了一组低内应力的试验参数组合。

1 试验准备

1.1 试验参数

电铸镍具有良好的力学性能，因此常被用做高精密仪器的元件，如X射线分析仪。而对于高精密仪器，电铸内应力过大将影响其检测精度，因此需要研究镍电铸基础工艺参数制造出低应力的镍电铸薄壁件。镍电铸主要使用的电铸液主要有硫酸盐系列和氨基磺酸盐系列，氨基磺酸盐系列的电铸液有利于得到低内应力的沉积层，因此选择氨基磺酸盐系列的电铸液，参数如表1所示。

表1 试验参数Tab.1 Test parameters

对于镍电铸工艺，电流密度、温度、氨基磺酸镍浓度是显著影响因素。硼酸作为PH缓冲剂，用于维持电铸过程中的PH值，避免PH值升高，电铸液的导电性能下降；氯化镍作用导电盐，主要用于提高电铸液的导电率，促进阳极正常溶解；十二烷基硫酸钠作为表面活性剂，可以有效降低电铸液的表面张力和粘度，改善沉积层的表面质量，避免出现针孔。

1.2 试验样件

阴极、阳极几何参数通过影响阴极表面电流密度，间接影响沉积层的内应力。平行板之间的电场分布均匀,为降低几何参数对内应力的影响，探讨电铸镍工艺中主要工艺参数（电流密度、电铸温度以及氨基磺酸镍浓度）对内应力的影响，以2cm×5cm×1cm的纯镍片为阳极、2cm×5cm×0.1mm的纯铜片为阴极（阴阳极间距3cm）进行内应力测试试验。实验前需对铜薄片一侧进行绝缘处理，另一面进行除油（乙醇）和去除氧化膜（盐酸）和处理。

1.3 弯曲阴极法测镀层内应力

弯曲阴极法是测量沉积层内应力最简单的方法，其原理是一面绝缘处理的平薄金属片的弯曲程度与镀层的作用力和基体材料的弹性模量之间存在一定的函数关系，其关系式如下所示。当阴极偏向金属阳极时，镀层的内应力为拉应力，反之，镀层的内应力为压应力。

σ

—— 沉积层的内应力(MPa)

E—— 基体材料的弹性模量(MPa),纯铜弹性模量为108000MPa

T—— 试片的厚度(mm),实验中为0.1mm

L—— 沉积部分的长度(mm)，实验中为50mm

t—— 镀层的厚度(mm)

Y—— 阴极自由端的偏移量(mm)

2 响应曲面试验设计

2.1 响应曲面法的原理和特点

响应曲面法是通过有限的参数组合试验拟合出显著因子与响应间的回归关系的一种统计学试验设计方法。通过方差分析确定回归模型的可靠性后，响应曲面可用于求解试验的最优方案。通常，响应分析只考虑不多于三个的显著因子的二阶交互作用，其表达式为：

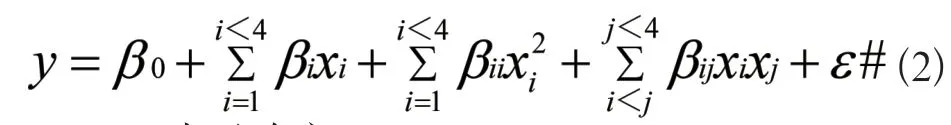
y

—— 表示响应；

ε

—— 表示误差；

x

—— 表示影响因子；

β

—— 表示回归系数，其中表示常数项，表示因子的一阶主效应，表示因子的二阶主效应，表示因子之间的交互作用。

中心复合表面设计CCF(Central Composite Face-Centered Design)是响应曲面试验设计的一种方法。该设计的试验点由角点、中心点以及面中心点三个部分构成，如图1所示。

图1 中心复合设计示意图Fig.1 Schematic diagram of central composite face-centered design

2.2 试验计划与响应

温度通过水域加热控制，难以得到低于室温的环境；氨基磺酸镍浓度过低时，高电流密度将导致阴极基体烧焦；为保证镀层的平均厚度相同，需要根据不同电流密度

J

调整电铸时间（

J=1,

电镀

120min;J=2,

电镀

60min;J=3,

电镀

40min

）。为不影响试验的进行，降低试验难度，选择CCF设计试验，试验计划及响应如表2所示。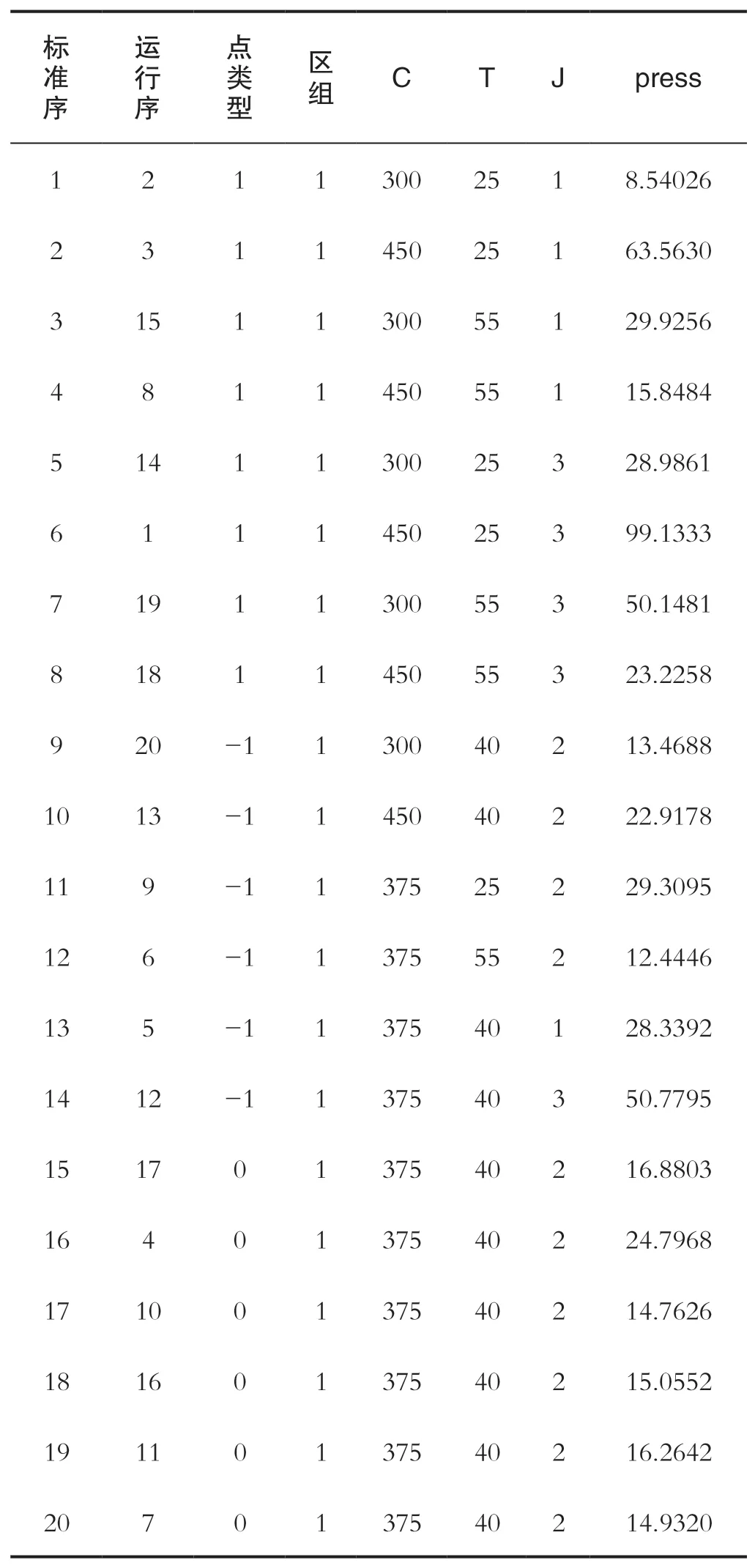

表2 响应曲面试验设计和结果Tab.2 Response surface test design and results

3 构建模型及优化求解

3.1 构建模型

使用完全二次模型对因子和响应进行拟合响应曲面，得到如表3方差分析。

表3 方差分析1Tab.3 Analysis of variance 1

响应曲面基于95%的置信区间假设，当P值大于0.05时，拒绝原假设（显著作用）。方差分析显示得到的回归模型中，C*C、T*T、C*J三项对内应力的作用并不显著，因此重新构建模型，从完全二次模型中去除上述三项，得到新的方差分析表如表4所示。

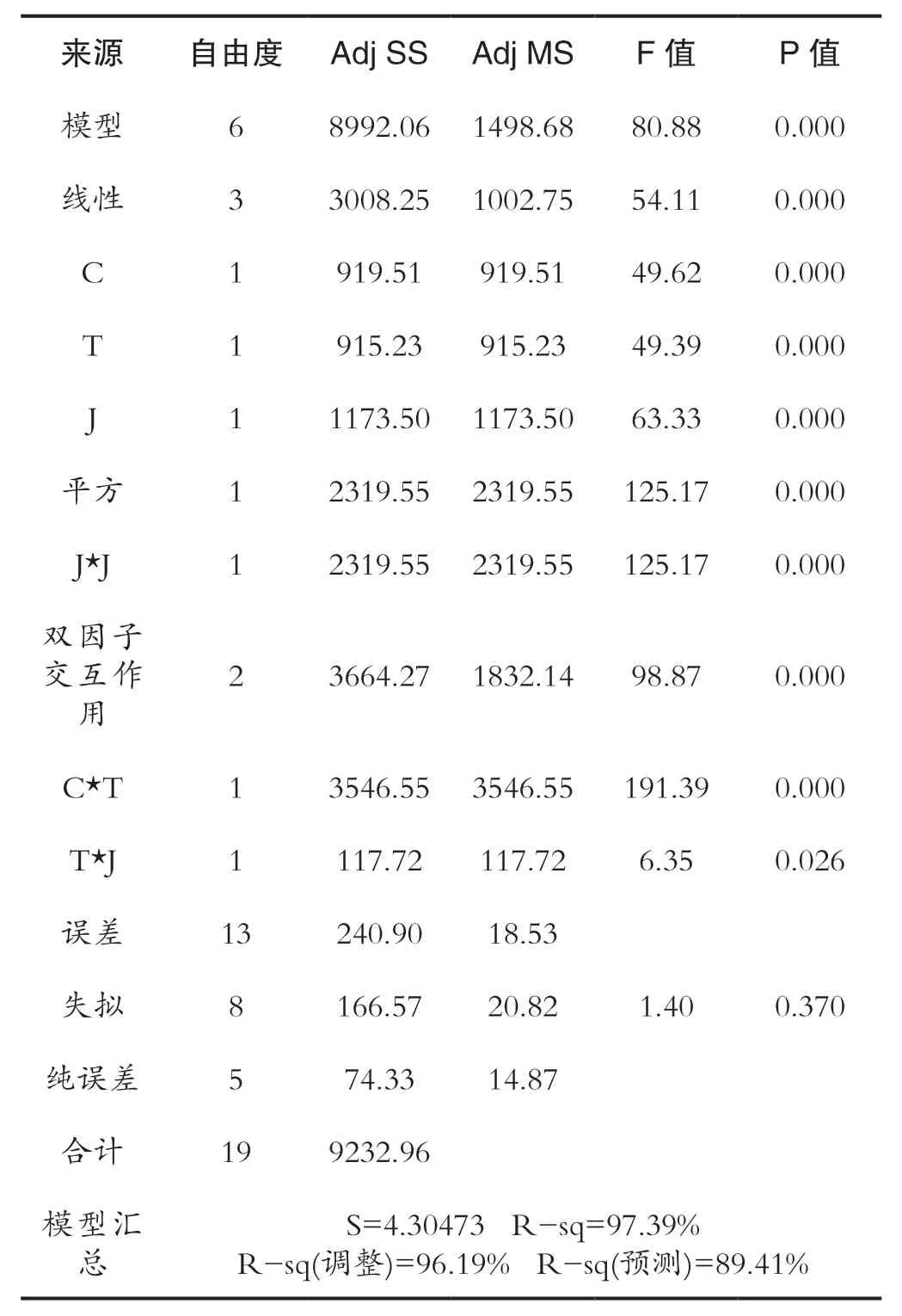
表4 方差分析2Tab.4 Analysis of variance 2

拟合回归方程为：

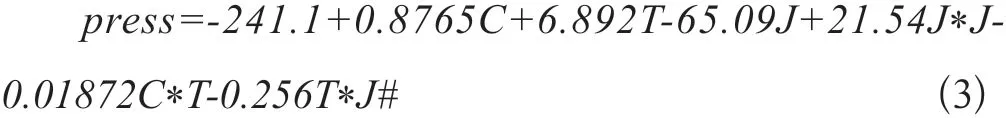
新模型中各项对应的P值均小于0.05，即各项均为显著项；“失拟”项对应的P值为0.370>0.05，表示模型并未失拟；表中多元相关系数R-sq接近于1，说明回归方程的相关性较好；修正的多元相关系数R-sq(调整)与R-sq较为接近，表示试验相对可靠、精度较高。观察模型对应的四合一残差图，并无异常，如图2所示。综合方差分析和残差图，该模型是有效的。

图2 残差图Fig.2 Residual diagram

3.2 优化求解

通过响应曲面得到的回归方程，进行“望目”优化，得到内应力接近0MPa的参数组合：

C=300g/L

、

T=25℃

、

J=1.14A/dm^2

。通过实验验证其内应力为5.58MPa，在其95%的置信区间(-6.59,7.24)内，且该实验参数组合测得的内应力优于当前响应曲面中的所有组合。如图3所示，对比

C=300g/L

、

T=25℃

、

J=1.14A/dm^2

（图a，内应力5.58Mpa）和

C=450g/L

、

T=25℃

、

J=3A/dm^2

（图b，内应力99.13Mpa）的样品沉积层放大一千倍时的微观结构：图a沉积层表面更加粗糙，晶体之间的分界明显；图b沉积层晶粒细化，晶体之间的分界不再显著，表面甚至出现多处晶粒聚集成块。高氨基磺酸镍浓度和大电流密度参数组合，促进了晶粒之间聚集（局部位置体积增大），使得沉积层内应力显著增大；此外，晶粒间无规则分布、位错显著也是导致内应力显著增大的一个原因。

4 结语

相比正交实验，响应曲面能够得到相对可靠的回归关系，用于优化响应分析。通过对电流密度、温度以及氨基磺酸镍浓度三个因素的响应试验设计，得到一组较低内应力的试验参数组合：

C=300g/L

、

T=25℃

、

J=1.14A/dm^2

。