基于大规模网络的结构能控性指数算法*

东华大学信息科学与技术学院 曾涛 李晓丽

传统的网络能控性是在给定输入下通过能控性判据来判断该网络是否可控，或是寻找使有向网络达到可控时的最少驱动节点集。为了研究网络达到可控时的链路长度，对于一个没有给定输入的有向网络，本文通过对节点度的研究和删除边等操作将有向网络分解成多条控制链，将控制链的根节点作为整个网络的驱动节点集。同时引入能控性指数的概念，对控制链长度进行研究。最后基于节点的度提出了一个算法将有向网络分解成独立可控的控制链,得出网络的驱动节点集和结构能控性指数，通过对大规模随机网络和真实网络的仿真，验证了算法的有效性。

现代网络科学中最具挑战性的问题之一是对复杂网络的控制。由于复杂网络具有高维度、非线性等特征，许多研究人员致力于了解复杂网络的结构以及节点间的相互作用，但是目前还有特定的框架来解决网络拓扑结构和非线性动力学之间的极其复杂的相互作用问题，因此复杂网络的控制依旧是一个复杂的问题。

Liu等人作出了开创性的贡献。提出了最小输入定理来有效地表征有向网络的结构可控性，通过识别最少驱动节点集以实现网络的完全控制。在此基础上将有向网络的结构可控性映射到最大匹配的问题上，通过给不匹配的控制节点施加控制使网络可控。但是，最大匹配并不是唯一的，所以在最大匹配的基础上提出了一个算法用于查找所有可能的输入节点使复杂网络可控。开发了一个精确的可控制性框架以替代结构可控制性框架，它提供了一种通用工具来处理具有任意结构和链接权重的复杂网络的可控制性，包括有向，无向，加权和无权网络自循环。结构可控性可以通过精确的结构矩阵框架来再现。通过为定向链接分配随机权重来确保结构可控性，证明了独立的驱动节点或外部控制器的最小数量等于网络矩阵所有特征值的最大几何重数。

在复杂网络中，节点也是至关重要的存在，很多研究表明驱动节点的选取与度的分布存在关系。发现驱动节点的数量主要由网络的度分布决定，对于密集的网络往往只需要几个控制节点，相反最难控制的是稀疏的不均匀网络，并且驱动节点的选取往往都避开高阶节点。根据每个节点在网络中的作用对节点进行了分类，将节点分为了关键节点，间歇性节点和冗余节点并开发了一个分析框架来识别每个节点的类别，从而发现复杂系统中两种不同的控制模式：集中控制与分布式控制。早在1974年，lin提出了“仙人掌”结构模型，并且提出“扩张”这一概念，指出节点和边的扩张会使网络变得不可控。网络中最重要的结构是连接节点和边的位置，它们确定系统的哪些部分在受到外部控制信号的影响时可以最终控制整个网络的行为，扩张是网络中产生控制输入需求的扩展点，通过扩张能够清楚地了解哪些节点是替代选择以及这些替代选择如何在整个网络中相互关联。

研究复杂网络时，对节点和边的思考是非常重要的，本文研究的重点是，对于一个给定的有向网络，由于密集网络不容易控制，稀疏的网络更容易控制。因此，通过对节点度的选取和边的删除将网络分解成多条控制链，通过选取控制链的根节点得出驱动节点集。同时结合结构能控性指数K的概念，对控制链的长度进行研究。

1 理论基础

1.1 能控性指数K

(A,B)

是一个拥有N个状态节点和M个控制输入的时不变网络系统：

其中

x(t)=(x(t),x(t),...,x(t))

表示t时间下的状态向量，A是N×N维系统矩阵，用来描述各个节点之间的连接关系和连接强度。B是N×M维输入矩阵，用于描述N个状态节点和M个控制输入之间的连接关系。若忽略网络边的权值，用“×”代表非零向量，此时的矩阵称为该系统的结构矩阵。引理:（

Kalman

秩判据）：系统（

1

）完全可控的充分必要条件为系统的能控性判别矩阵：

C=[B,AB,...,AB,AB,...,AB]

满足：

rank(C)=N

但是，由于能控性判别矩阵

C

不是每列都是线性无关的，可能存在某些列线性相关，使得能控性判别矩阵

C

在

(K+1)M

列时就已经满秩了。因此我们可以得到一个

N×(K+1)M

矩阵

Q

，并且

Q

满足：

Q=[B,AB,...,AB]

。

由此我们可以推导出能控性指数的概念。

定义：若系统(1)满足(2)和(3)这两种情况时，这里的

K

称为该系统的能控性指数。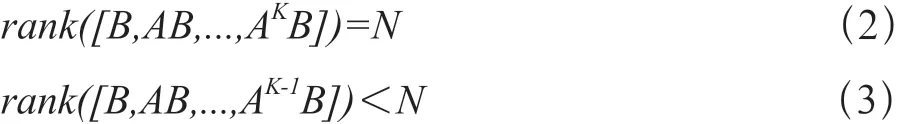

1.2 结构能控性指数K

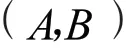
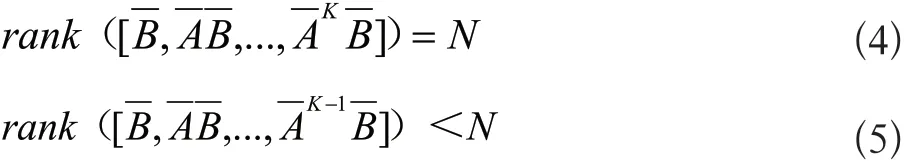
显然，这里的K≤N，表示结构能控性指数K不超过N。结构能控性指数K的物理意义表示从网络系统的控制节点出发通过K次的信息传递可以影响到所有节点，即网络达到可控状态。

2 基于控制链的结构能控性指数

如图1所示的结构我们称为控制链，也称之为路径，控制链是可控的，且从控制链的结构很容易看出控制链的结构能控性指数K为控制链总节点的数量减1。如图1所示的控制链有4个状态节点，所以其结构能控性指数为3。

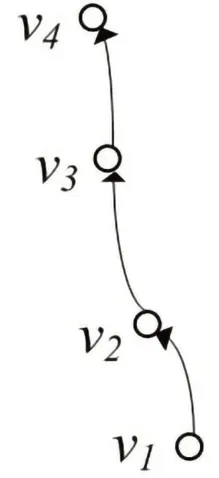
图1 控制链Fig.1 Control chain

若一个有N个节点的系统(A,B)对应的结构为控制链且控制链可控，那么该控制链的系统矩阵A和控制矩阵B可以表示为：

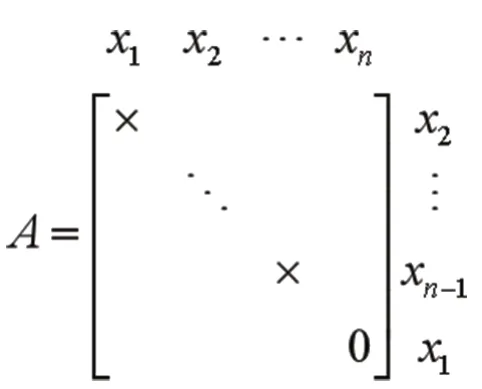
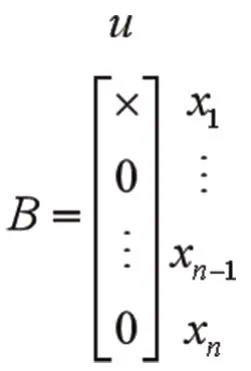
矩阵中非零元素“×”表示节点之间的连接关系和强度。显然，系统(A,B)的能控性指数为N-1，且满足式子：

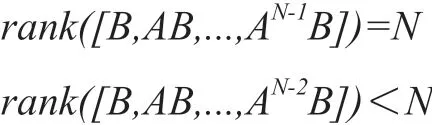
3 Knode算法

由上文可知控制链是可控的且结构能控性指数为N-1，同时，稀疏网络和稀疏的节点是容易控制的，对于一个密集网络或者复杂网络，可以考虑将其不断的简化。因此该算法的最终目的是将复杂的有向网络分解成若干条控制链，网络的驱动节点集为所有控制链根节点的集合，整个网络的结构能控性指数为最长控制链的能控性指数。

对控制链结构来说，根节点的入度为0，出度为1，我们将所有入度为0的节点作为驱动节点；控制链末端的节点入度为1，出度为0，所以，出度为0的节点当做末端节点；其余节点的入度和出度都为1，且控制链所有节点的入度和出度都不超过1。因此，对复杂网络进行分解时可以参考这个规律，对入度或者出度大于1的节点进行边删除，在此基础上通过寻找最短路径来限制控制链的长短，使得网络的结构能控性指数不至于过大。本文提出基于节点度的网络分解算法步骤如下：

步骤1：初始化集合S={}，将网络中节点入度大于等于2的节点记为v(0≤i≤N)，将v存入集合S。

步骤2：随机选取S中节点v进行回溯，回溯至入度为零的节点为止，选取其中路径最短的一条链路，记为L。若最短的链路不止一条，则随机选取一条。

步骤3：将步骤2中找出的最短链路L进行保留，删除其他一步可达L的链路和L（除节点v外）可达其他节点的链路。

步骤4：遍历集合S中所有入度大于等于2的节点直到不存在入度大于2的节点为止。

步骤5：初始化集合S={}，将网络中节点出度大于等于2的节点记为o(0≤i≤N)，将o存入集合S。

步骤6：随机选取S中节点o向下寻找至出度为零的节点为止，选取其中路径最短的一条链路同时删除与该链路无关的其他链路。

步骤7：遍历集合S中所有出度大于等于2的节点直到不存在出度大于2的节点为止。

4 仿真结果分析

利用本文提供的算法对大规模ER随机网络进行仿真，表1为仿真结果。N为网络节点的个数，L为网络的边的总数，为ER随机网络的平均度。令n=N/N来表示网络系统的控制输入情况，nm为最大匹配算法下得到的值，nn为文本提供的算法下得到的值。K是最大匹配算法下的结构能控性指数K值（控制链路的最大长度），K为本文算法下的结构能控性指数K值。真实网络数据集仿真结果如表2所示。

通过表1可以看出，本文提供的算法和最大匹配算法拥有相同的最少驱动节点使得网络的结构能控性指数K，本文算法的优势在于，在相同网络和相同的驱动节点下，本文提供的算法拥有更小的结构能控性指数K值，即控制链路相对更短，控制速度更快。同时，针对不同规模的随机网络，当网络的平均度值相差不大时，n的值变化不大。说明最小控制输入与网络的平均度相关。表2针对不同的真实网络进行了仿真，所有的真实网络数据集来源于文献，对于表格中的网络基本信息，其中Type表示网络的类型，Name为网络的名称，其他数据与表1保持一致。从表2可以看出，对于真实网络，算法拥有和最大匹配算法一样的最少驱动节点，网络可控时的结构能控性指数K值更小。同时可以看出网络平均度相差较大时n的值差距也较大，验证了网络的平均度影响网络的最小控制输入，通过仿真结果验证了算法的可行性，为真实网络驱动节点的选取和控制性能研究提供了一定的参考价值。

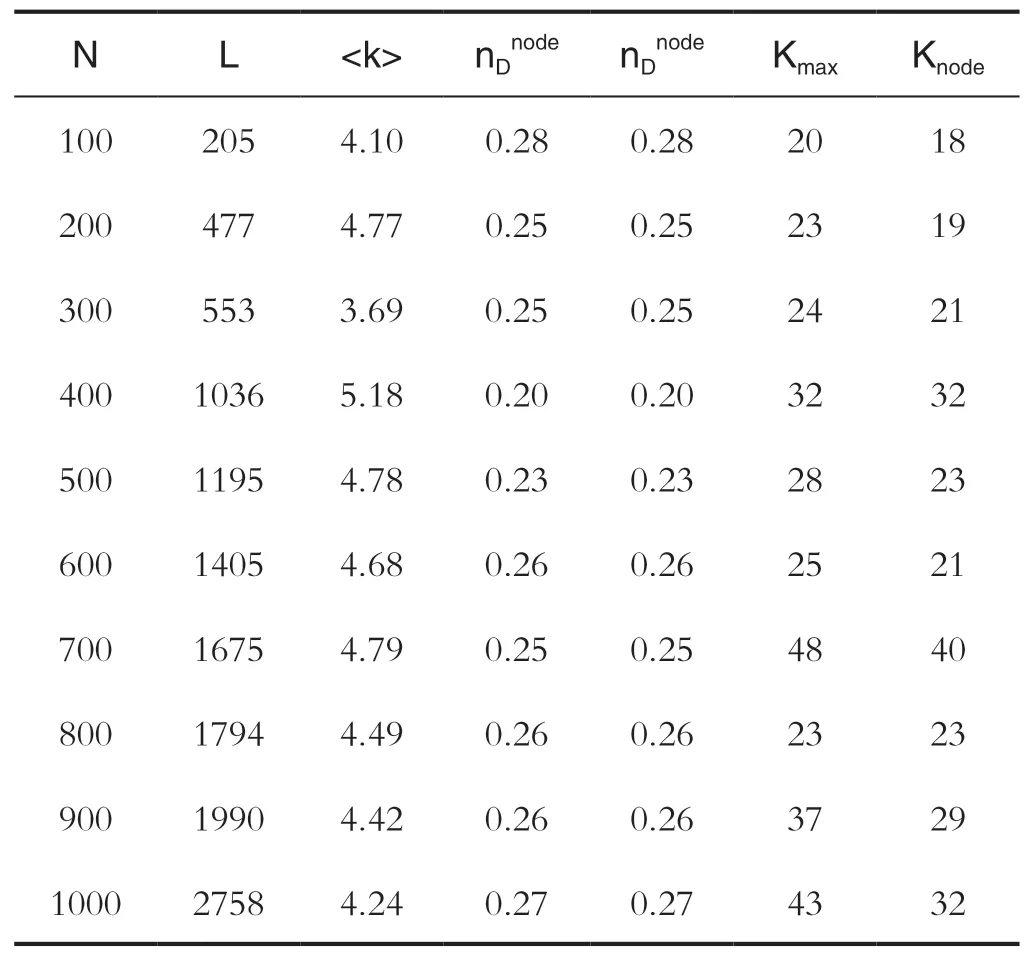
表1 ER随机网络仿真结果Tab.1 Simulation results for ER random networks

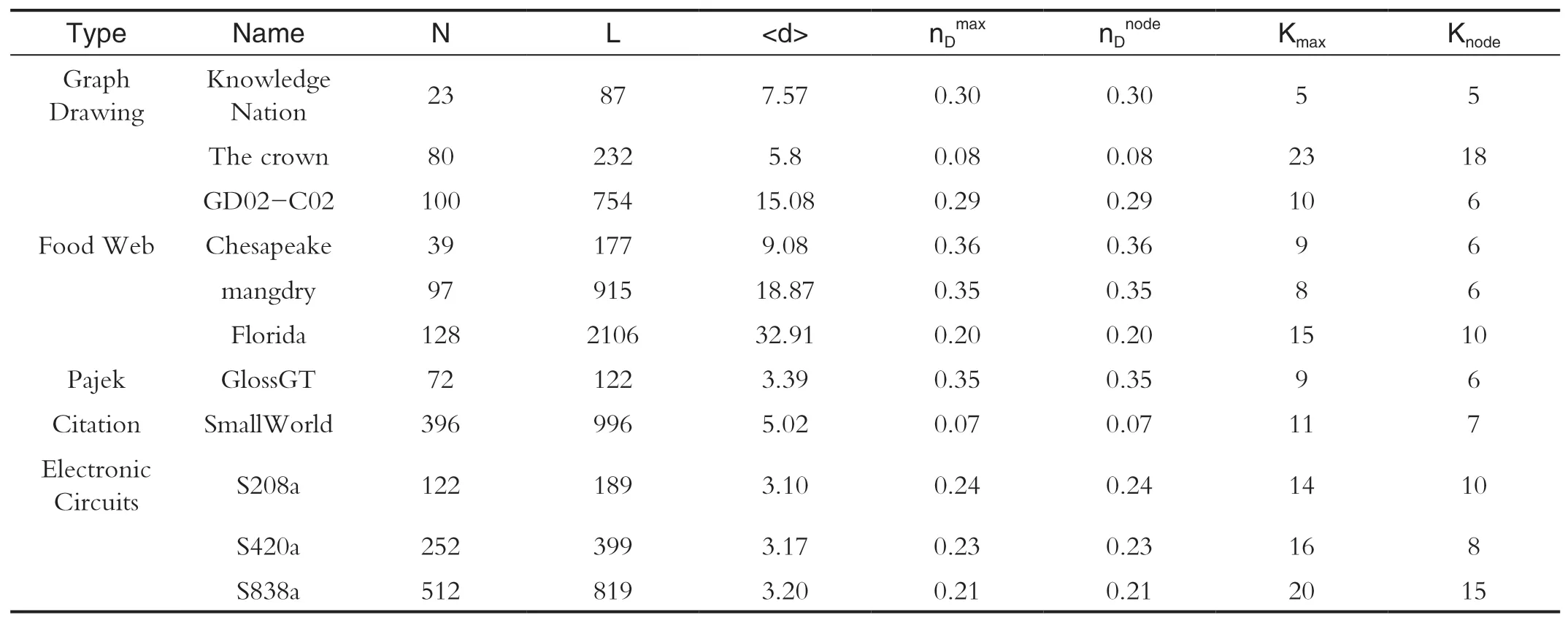
表2 真实网络数据集仿真结果Tab.2 Simulation results for real networks

5 结论

本文通过对节点度以及结构能控性指数的思考，将有向网络分解为能控的控制链结构，把分解后的控制链的根节点作为驱动节点，所以复杂网络的驱动节点集就是分解后控制链根节点的集合，并且很容易看出可控时网络内部的连接情况。再结合结构能控性指数K对控制链的长度进行了讨论，得出了最长控制链的能控性指数就是该网络的结构能控性指数。最后，提出了一个将网络分解为控制链的算法，通过对大规模随机网络和真实网络的仿真验证了该算法的有效性，为实际网络驱动节点的选取提供了参考。