复合间接式胎压监测机制研究
2022-03-08吴飞龙郭世永
吴飞龙,郭世永
(青岛理工大学 机械与汽车工程学院,青岛 266525)
米其林于2006年在“开车前思考”安全运动中进行的一项调查显示,在接受检查的20 300辆汽车中,只有6.5%的车4个车轮均具有所需的轮胎压力[1]。早些年有很多直接胎压检测的方法,这些方法往往有很多弊端,近年来,随着ABS系统的广泛应用,间接式胎压监测系统问世。间接式胎压监测系统(TPMS)是通过测量与轮胎压力相关的状态变量,建立其与胎压变化的对应关系[2]。间接式胎压监测系统一般是通过ABS轮速传感器测得轮速信号,采用相关算法对轮速信号进行处理来识别胎压变化,进而实现胎压监测[3-4]。目前,我国胎压监测系统的市场占有率小,国产汽车在此方面的普及率低,胎压监测系统仍处在萌芽期[5]。而间接式胎压监测系统不需要配备外加传感器,所以具有广阔的发展前景和深远的研究意义[6]。
现阶段,国外采用的间接式胎压监测系统监测算法大多为频谱分析法、半径法和动力学模型法3种方法[7]。其中频谱分析法和半径法最为常见,频谱分析法通过傅里叶变换将振荡的轮速信号转化为变化的频率信号,通过车轮速度频谱的变化来估计胎压的变化情况;半径法先通过轮速传感器测得不同车轮的轮速信号,通过比较不同车轮的轮速来检测轮胎半径的变化。
本文综合考量了频率法和滚动半径法的特点。频率法利用在一定范围内轮胎的共振频率越大,胎压越大的机理,通过与正常胎压下的共振频率作比较,从而判断出轮胎的胎压情况;滚动半径法利用在一定范围内滚动半径越大,胎压越大的原理,由各车轮轮速来推导出轮胎的滚动半径,然后将其进行归一化处理,通过相对滚动半径来判断出轮胎的胎压情况。
1 面向胎压监测的轮速信号处理
1.1 轮速信号的采集
本文基于Db9接口的CAN总线测试系统实现对轮速信号的采集,一共采集了000—026组数据,以报文的形式发出,如图1所示。

图1 报文
报文中的数据每个id对应8组数据,依次对应前后左右4个轮胎的轮速信号,每组数据分别由2个字节组成,对应高电位和低电位,每个轮胎的原子数=256×(高电位+低电位)。
将算得的原子数分别按照前、后轮整理到一起,假设本次数据是由齿数为n的速度传感器齿圈旋转k+1圈采集到的数据,取其中的4(kn+1)为一个矩阵(图2),其中第1行至第4行分别代表4个轮的原子数。
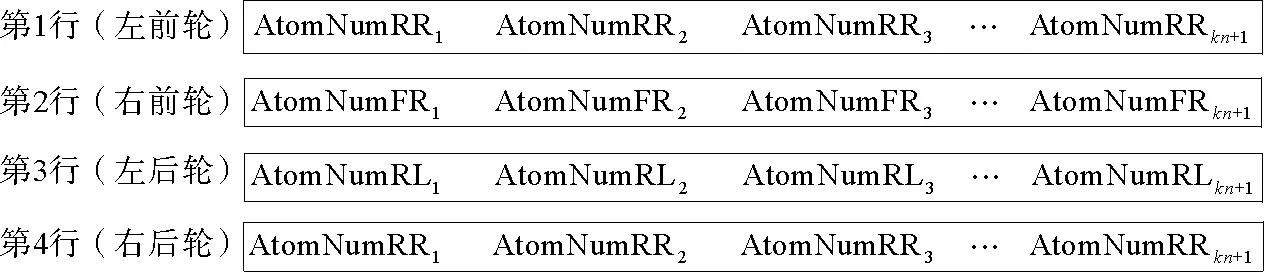
图2 原子数
1.2 剔除错齿
原则上脉冲间隔tj=(AtomNumXXj+1-AtomNumXXj)×3.2 μs,故得到一个4×kn的脉冲间隔矩阵,如图3所示。

图3 脉冲间隔矩阵
实际采集到的原子数数据存在少识别齿和多识别齿的情况,所以需要剔除错齿。当0≤原子数差值≤0.2×上一组原子数差值时,为多识别1个齿的情况,直接去掉多识别的齿即可;当1.6×上一组原子数差≤原子数差值≤2.6×上一组原子数差值时,此时为少识别1个齿的情况,则2个错齿分别用上一圈同位置齿的原子数差值代替。将修正后的原子数差值转化成脉冲间隔。
1.3 齿圈误差辨识与消除
轮速传感器系统测量误差主要由两部分组成:一是系统时间误差,二是齿圈角度误差。文献[8]已经证明,计时器精度引起的系统误差对轮速传感器来说可以忽略不计。
齿圈由于加工精度的不足总会存在形变误差,这样会导致齿的实际角度φj不等于圆周角除以齿数,即φj≠2π/z(z为齿数),每个齿造成的角度误差值往往是随机的,齿圈误差将直接影响轮速计算结果的准确性。因此,需要对齿圈误差进行一定程度上的消除。
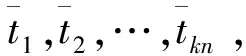

(1)
式中:tj为每一圈经过每个齿的修正时间;j为齿数;p为圈数。
齿圈中每个齿的单圈误差以及经过k圈后累加的误差均值分别为
(2)
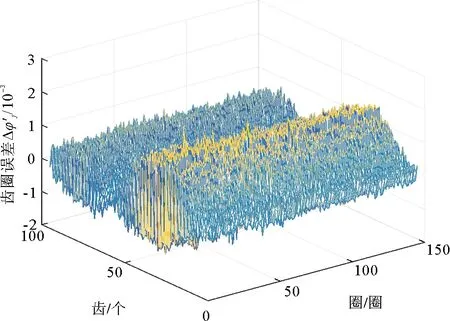
图4 齿圈误差
(3)
故消除误差的齿圈角度为φj=2π/z+Δφj。
2 基于频率法的胎压监测
频率法的流程如图5所示。
2.1 轮速的计算
本文采用频率法求轮速:
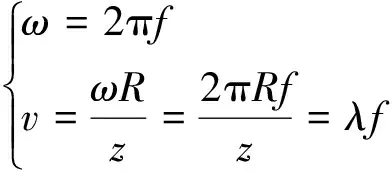
(4)
式中:v为轮速;R为车轮半径;z为齿圈齿数;ω为角速度;f为轮速信号的频率。
2πR/z,即λ对于一个确定的系统而言为常数,本文车轮半径R=0.393 m,齿圈齿数z=38,算得λ=0.065,取λ=0.07,故轮速

图5 频率法流程
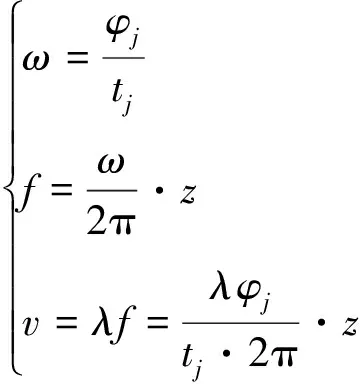
(5)
2.2 基于均匀插值的轮速信号重构方法
在胎压监测系统的轮速信号重构算法中,就是将修正的轮速信号ω(t1),ω(t2),ω(t3)…转换为等时间间隔的ω′(t0),ω′(t0+T),ω′(t0+2T)…[6]。利用分段线性插值法进行轮速信号重构,如图6所示。

(6)
2.3 轮速信号的筛选
在汽车传动系统内不可避免地存在包括发动机力矩、传动轴扭矩等引起的传动系扭振,这些扭振引起的噪声振动频率要远高于轮胎的共振频率,从而会导致轮胎的共振频率无法准确地提取,进一步影响胎压监测的精度。因此在进行轮速信号的筛选时要尽量消除传动系扭振的干扰,来提高胎压监测的精度。
参考文献[7]减少传动系扭振的方法,为了判断获取的轮速信号内是否受传动系扭振的干扰,本文建立了用于计算驱动轴车轮轮速噪声的相关系数,其表达式为
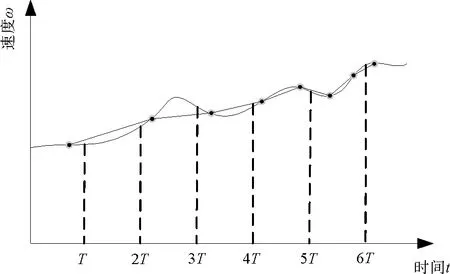
图6 重构轮速信号

图7 频谱
(7)
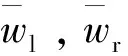
式(7)分子为轮速噪声的协方差,分母为轮速噪声的标准差。
根据相关系数对轮速信号作进一步筛选,筛选条件为:只有当相关系数r 首先利用傅里叶变换将滤波后的时域信号转换到频域信号,为共振频率的估计做准备。如图7所示,在频谱图中有2个频率区间是与轮胎压力相关的,其中一个是低频区间,一个是高频区间[9]。 Yi=ai(x-xi)3+bi(x-xi)2+ci(x-xi)+di (8) Y′i=3ai(x-xi)2+2bi(x-xi)+ci (9) Y″i=6ai(x-xi)+2bi (10) 三次样条曲线在[xi,xi+1]上是三次多项式,且应满足连续性条件、一阶导数连续条件、二阶导数连续条件,最终可以推导出: (11) 其中,li=xi+1-xi,li-1=xi-xi-1,b0=bn=0,从而得到下列形式: (12) 将方程(12)化为矩阵形式为Rb=QTd L写成矩阵形式为 (13) 将b=R-1QTd代入式(13)得 (14) 令L′(d)=0,求得 (μQT∑Q+R)b=QTyd=y-μ∑Qb (15) 其中,μ=2(1-λ)/3λ。 对曲线进行平滑处理后的结果如图8所示。 利用均值法估计轮胎的共振频率,当分析的车轮是前轮时,在35~45 Hz内找振幅最大值A,并以最大振幅为中心向两侧寻找振幅为0.8A对应的频率f1与f2,以f1与f2的平均值(f1+f2)/2作为轮胎共振频率;当分析的车轮是后轮时,在42~50 Hz内找振幅最大值A,并以最大振幅为中心向两侧寻找振幅为0.8A对应的频率f1与f2,以f1与f2的平均值(f1+f2)/2作为轮胎共振频率。得到的结果如图9所示。 图8 平滑后的频谱 用上述方法分别对000—026组数据(其中有几组数据异常,已被剔除)进行仿真,得到一系列估计的共振频率,000—005组是已知正常胎压下测得的共振频率,测得的正常胎压(如006组)、一轮欠压(如010组)、两轮欠压(如016组)、三轮欠压(如019组)和四轮欠压(如026组)下的情况,分别如图10—14所示。 将上述仿真的结果导出数据,如表1所示。 以正常胎压的共振频率为标准,若估计的共振频率比正常胎压时的共振频率减小2.5 Hz,则车轮欠压,否则不欠压。根据表1可以得出结论:一轮欠压的仿真效果不明显;016左前轮和右前轮欠压;019右前、左后和右后三轮同时欠压;022~026四轮均欠压。 当汽车某一个轮胎欠压或两个轮胎欠压时(尤其一个轮胎欠压时),频率法有时候识别不出,从而影响胎压监测的准确度,此时将采用滚动半径法。滚动半径法包括采集轮速信号、剔除错齿、消除齿圈误差、计算轮速、计算总路程、计算滚动半径6个步骤。前4个步骤与频率法相同,图15为滚动半径法的流程。 表1 4轮共振频率 Hz 图15 滚动半径法流程 采集到的数据经过上述步骤后,得到的滚动半径如图16所示。 将仿真的结果导出数据,如表2所示。将各组四轮所测得的滚动半径分别与正常胎压下的滚动半径做一个比值,然后将各组所得的比值做归一化处理。归一化的具体过程是:将每组所得的比值最大的值化为1,其他3个轮的比值除以这个最大的比值,从而得到一个接近于1的数。评判标准是:最后归一化的数在0.9994~1的范围内对应的轮胎为正常胎压,小于这个范围的数对应的轮胎为欠压。 由表2可以得出结论:010,011,013,014左前轮欠压;012左前和左后欠压;015—018左前和右前轮欠压;019右前、左后和右后轮均欠压。 表2 4轮相对滚动半径 cm 本文采用了一种基于频率法与滚动半径法相结合的综合间接式胎压监测算法,当4个轮胎中只有某1个轮胎单独欠压或有任意2个轮胎欠压时采用半径法,其余所有情况均采用频率法,这种方法能有效地监测出胎压正常及不正常的各种情况,同时既能降低直接式胎压监测的成本,又能减少胎压对汽车操纵稳定性、平顺性以及动力性的影响。该算法性能好,可操作性强,经过处理能应用于胎压的实时监测,具有良好的应用前景。2.4 轮胎共振频率的提取


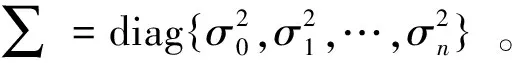
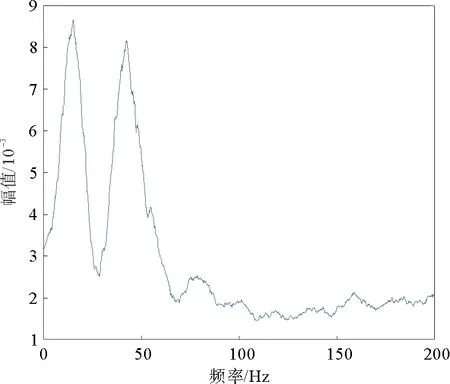
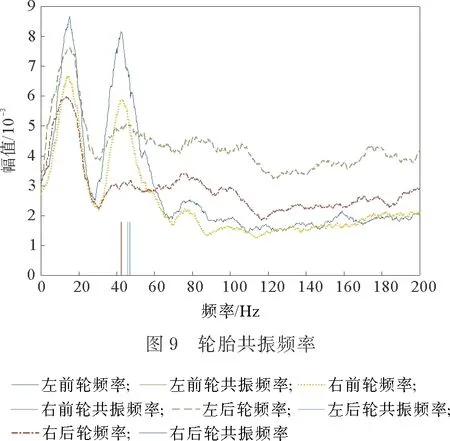
3 基于滚动半径法的胎压监测

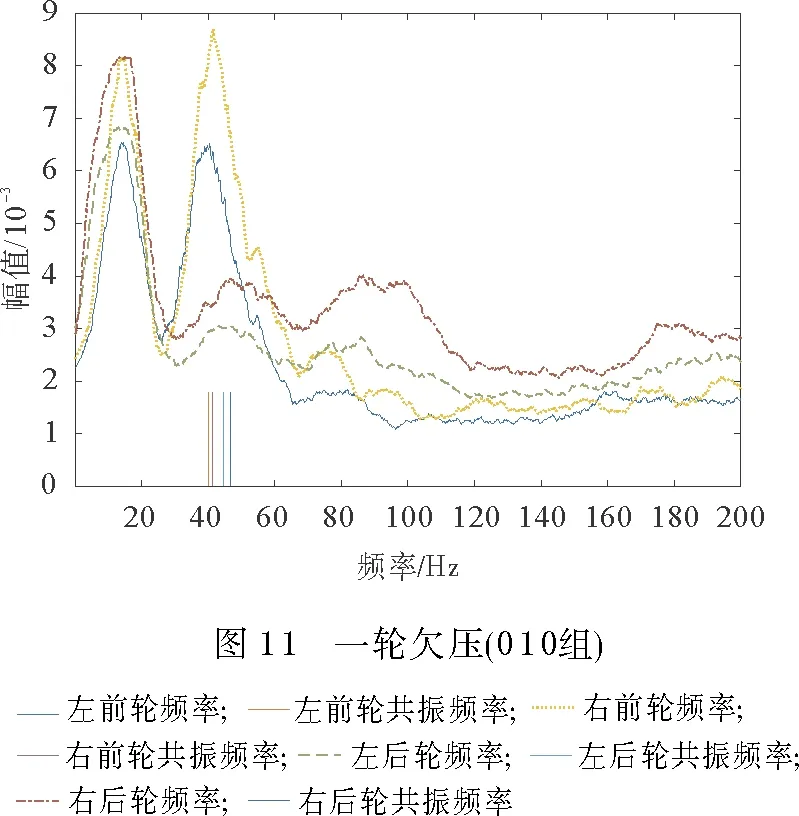
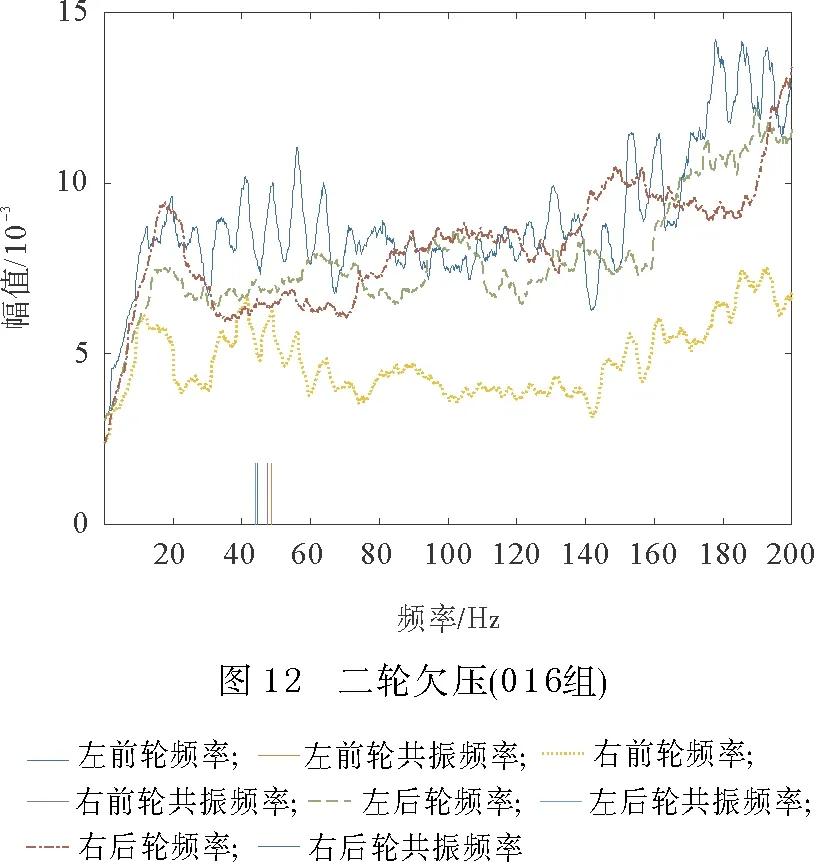


4 结束语
