单基地互质MIMO 阵列DOA 估计

周 围，冉靖萱，彭 洋，陈星宇，马茂琼

（1.重庆邮电大学 光电工程学院，重庆 400065；2.重庆邮电大学 移动通信技术重庆市重点实验室，重庆 400065）

0 引 言

单基地大规模多输入多输出（Multiple⁃Input Multiple⁃Output，MIMO）雷达是近年来在通信领域中广泛使用的新型雷达，其凭借着高速、稳定等优点，成为了5G 通信系统的核心技术。MIMO 雷达使用多个阵元同步发射和接收信号以执行集中信号处理，这对于在诸如提升信道容量、提高信号检测和目标参数估计性能等方面具有显著的优势。

波达方向（Direction of Arrival，DOA）估计在通信、医学成像、天文成像、地震学、声呐等领域有着广泛的应用。由于单基地MIMO 雷达具有同时估计相干和非相干目标的能力，因此DOA 估计是MIMO 雷达研究中的一个重要方向。近年来所提出的MIMO 雷达DOA 估计算法大都基于阵元间隔为半波长的均匀线性阵列，在这种情况下总的可分辨目标数为接收阵元数减1，可分辨的相干目标为发射阵元数，并且在大规模MIMO 阵列中很难在有限的空间内部署非常多的阵元，因此本文在MIMO 阵列中引入互质阵列，通过研究互质阵列的特点，用更少的阵元达到均匀直线MIMO 阵列需要更多阵元才能估计的目标数。

互质阵列是一种非均匀稀疏阵列，相比均匀阵列，互质阵列可以对入射信号进行欠采样，从而突破阵元之间的间距限制，并且阵列可以获得远超阵元个数的自由度（Degree of Freedom，DOF），但是这些方法中并没有考虑目标相干的情况。文献[11]对单基地MIMO 雷达进行了研究，得出了可以成功估计的相干目标和非相干目标的数量与阵元之间的关系。文献[12]将互质阵列引入MIMO 雷达，结合ESPRIT 算法进行DOA 估计，但该算法只能估计非相干目标。文献[13]介绍了一种互质MIMO 阵列的几何结构，文章从互质MIMO 阵列的原始数据中模拟出和协阵列（Sum Co⁃Array）的协方差矩阵，从而大大增加了互质阵列的DOF。

为了提高DOA 估计的性能，并且尽可能地降低算法的复杂度，本文重点针对互质MIMO 阵列估计阵列的几何模型进行了研究，找到了一种和协阵列，并利用多频操作对阵元进行扩展，提出基于MUSIC 算法的发射/接收和协阵列DOA 估计方法（T/R Co⁃Array DOA Estimation Method Based on MUSIC，TR⁃CA⁃MUSIC），通过重排列数据矩阵构造MUSIC 算法谱峰搜索需要虚拟的数据矩阵。对于个发射阵元、2-1 个接收阵元的互质MIMO 阵来说，该和协阵具有+-1 个连续阵元和2个中间只有一个孔的半连续阵元。通过改变发射阵元的信号发射频率，将半连续阵元中的两个孔洞用附近的阵元补齐，使得整个连续阵列阵元数目扩大为+3-1，该阵列最多可以估计+3-2 个非相干信号、(+3-1) 2 个相干信号。同时，为了避免MUSIC 算法中特征值分解带来的巨大运算量，本文引入传播算子，提出基于传播算子的发射/接收和协阵 列DOA 估 计 方 法（T/R Co⁃Array DOA Estimation Method Based on PM，TR⁃CA⁃PM）。其中：TR⁃CA⁃MUSIC方法的运算量较大，但可以同时准确估计相干和非相干目标；TR⁃CA⁃PM 算法在少目标情况下运算量大大降低，但其相干目标估计能力较弱，比较适合少量非相干目标的DOA 估计。最后本文分别给出了两种算法的空间谱图和均方根误差图，证明了两种算法目标数的估计能力，并验证了在信噪比（SNR）大于-5 dB 时，TR⁃CA⁃PM 的性能与TR⁃CA⁃MUSIC 接近。

1 系统模型

1.1 信号模型

假设和互为质数，且。单基地互质MIMO 阵列如图1 所示，该阵列包含了个发射阵元和2-1 个接收阵元，其发射和接收阵元的位置可表示为：

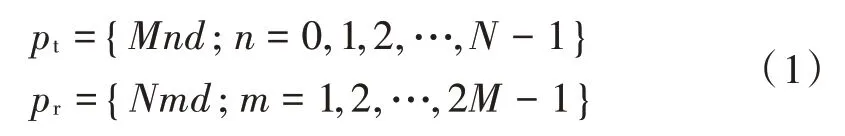
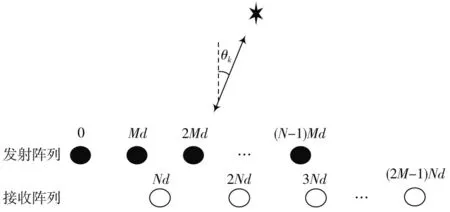
图1 单基地互质MIMO 阵列几何构型

考虑到等效虚拟阵列为均匀线阵，所以定义=2，为发射阵列发射的窄带信号的波长。

假设有个非相关目标和个相关目标位于阵列的远场，阵列的个发射器中的每个发射阵元都发射一个窄带信号照射目标，然后通过所有的2-1 个接收器收集所有目标的反射信号，从而形成一个(2-1) ×维的信号矩阵。

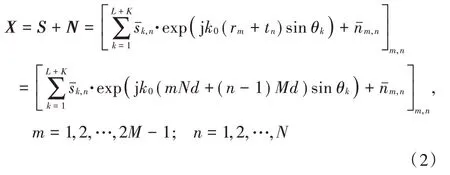
式中：第(,)项表示第个发射器发射并由第个接收器接收到的信号矢量；=c，为信号的波数，为发射阵元的发射角频率（信号角频率），c 为光速；r,t分别为接收阵元和发射阵元的位置；θ为第个目标的真实角度；ˉ是均值为零、方差为的高斯白噪声；ˉ可以表示为：

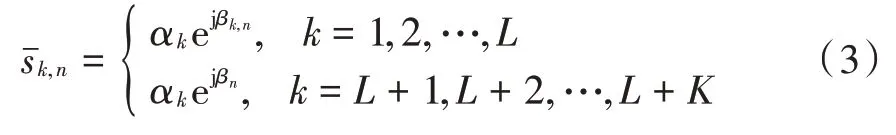
式中：α是信号的振幅；β是非相干目标的相位；β是相干目标的相位。因此的协方差矩阵为：

式中：[]表示期望运算；H 表示共轭转置。

1.2 和协阵列模型

传统MUSIC 算法只需要利用1.1 节中的协方差即可进行DOA 估计，但由于互质MIMO 阵列是稀疏阵列，阵元间距大于半波长，直接进行DOA 估计会产生相位模糊。

根据式（2）可知，原始数据的相位由发射器位置的和确定，所以可以找到想要的等价虚拟阵列，然后通过重新排列原始数据矩阵构造虚拟数据矩阵即可估计DOA。

图1 的和协阵列如图2 所示，可以看出该阵列并不是一个完整的连续线性阵，其中有一些孔洞并没有填充阵元，但可以将其划分为三个部分：阵列正中的连续子阵；紧挨连续子阵两旁的半连续子阵；最外边的非连续子阵。连续子阵占了该和协阵列的很大一部分，经计算，连续子阵包含+-1 个阵元，半连续子阵包含2-2 个阵元，从而，该互质MIMO 阵列利用+数量级的阵元数目达到了×数量级的自由度。

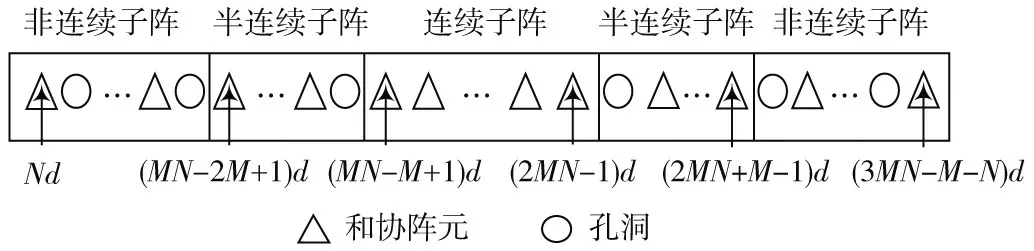
图2 单基地互质MIMO 阵列的和协阵列几何构型

1.3 多频操作延长连续子阵

如果将半连续子阵中的两个孔填上，则和协阵列就会多出2个连续阵元，自由度也将增加2。在单频率模式下虚拟形成的阵列孔可以通过多频率操作填充孔洞，以形成更长的连续子阵。由式（2）可得：

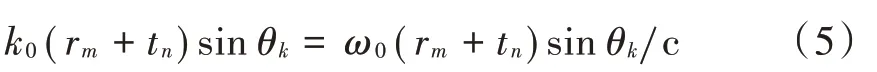
令工作频率ω=，则当工作频率为ω时，阵列流形的相位可以表示为：

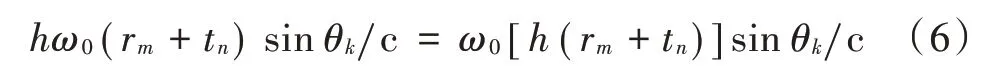
式中：(r+t)是频率为ω时和协阵列的位置，相比初始频率时的位置r+t，可以将新阵列视为原阵列按比例延伸倍。

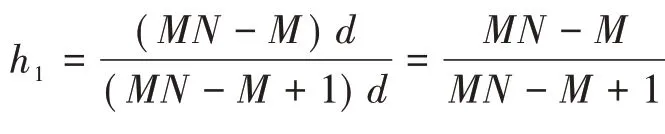
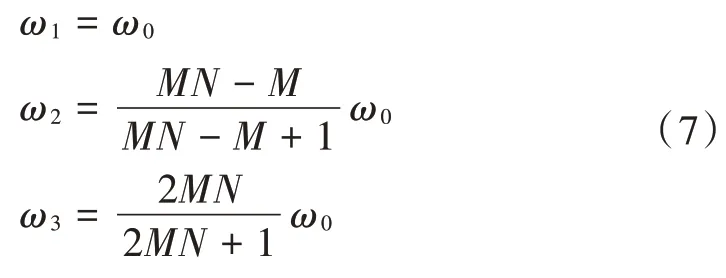
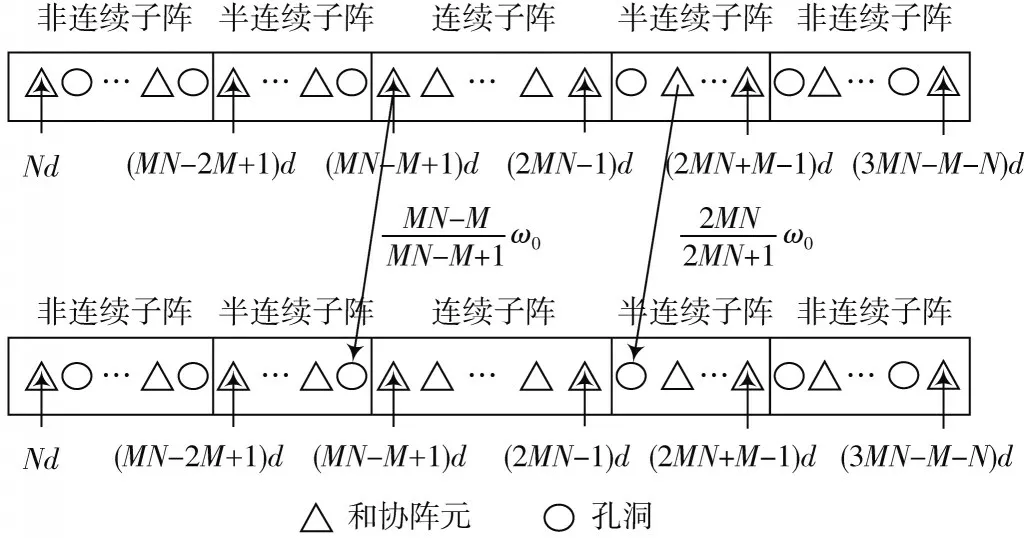
图3 三种工作频率下的和协阵列几何构型

2 DOA 估计

2.1 TR⁃CA⁃MUSIC 方法DOA 估计

扩展后连续子阵的位置可以表示为：

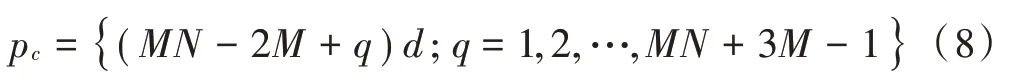
假设从连续子阵中取个发射阵元和个接收阵元，则发射和接收阵元的位置可以表示为：

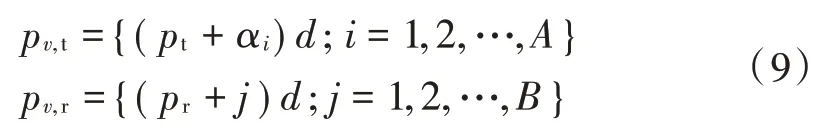
式中α为任意递增的正整数，也就是说相邻两个发射阵元的间距是不固定的。当满足式（10）时，虚拟阵列和连续子阵近似等价。

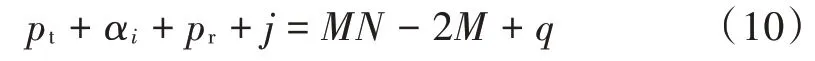
式 中 ： ∀∈[1,2,…,]；∈[1,2,…,+3-1]；∈[1,2,…,]。特别地，当α=时，连续子阵列包含的虚拟阵元数目最多，所以自由度最大，此时发射阵元和接收阵元的位置可表示为：

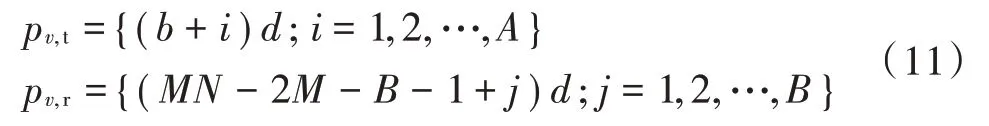
式中为任意正整数。根据不同的相干和非相干信号的个数，可以灵活地设置和的值。

接下来分四步进行DOA 估计：

1）写出和协阵列中+3-1 个连续阵元的数据矩阵。

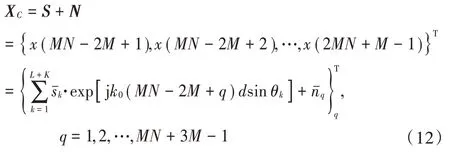
2）构造×维的数据矩阵X：

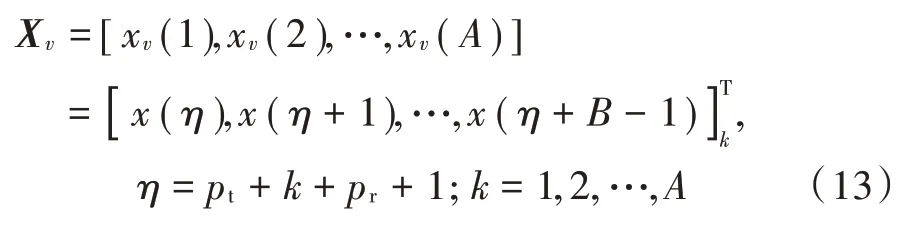
式中X由X的个连续元素组成。

3）将式（13）代入式（4）得到×维的数据协方差矩阵：

4）对R进行特征值分解，并利用MUSIC 算法进行谱峰搜索。

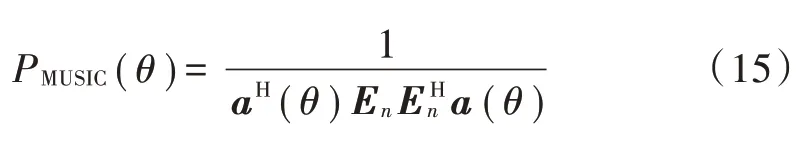
式 中：E是 协 方 差 矩 阵R的 噪 声 子 空 间；() =[1,e ,e ,…,e ]，是个接收阵元的阵列流形向量。

该方法有如下几个特点：

1）当＞＞1 时，最多可以分辨-1 个目标（包含相干和非相干），其中最多可分辨个相干目标。

2）当＞＞1 时，最多可分辨-1 个任意相干或非相干目标。

3）当=1 时，最多只能分辨-1 个非相干目标，且此时可以分辨的目标数最多。

2.2 TR⁃CA⁃PM 方法DOA 估计

以上的TR⁃CA⁃MUSIC 方法涉及到对×维的协方差矩阵R进行特征值分解，这会导致算法的计算量极大，影响算法的速度。传播算子算法（Propagation Method，PM）利用矩阵分块代替特征值分解获得噪声分量，可以有效避免特征值分解带来的巨大运算量，因此本文引入传播算子算法提出TR⁃CA⁃PM 算法。利用传播算子获得噪声子空间的步骤如下：

1）对R进行分块，有：

式中：[ ⋮ ]表示矩阵左右分块；为×(+)维矩阵，是R的前+列；为R的剩余项。

2）存在一个(+)×(-(+))维的矩阵，使得=成立，其中就是传播算子，由最小二乘法得：

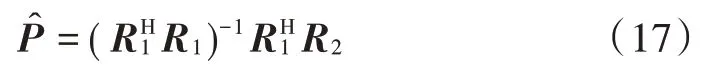
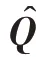
4）根据步骤3）构造谱峰搜索函数：

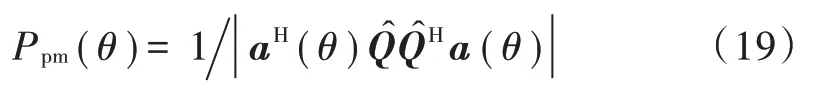
2.3 复杂度分析

TR⁃CA⁃MUSIC 方法的计算量主要是由协方差矩阵运算、特征值分解以及谱峰搜索带来的。假设将乘法运算次数看作复杂度，则其协方差运算式（14）的复杂度为(•)，特征值分解复杂度为()，谱峰搜索复杂度为((-(+) )+)( 1800 step )，其中，step 为搜索步长，本文取0.01。两种方法中的协方差矩阵运算和谱峰搜索的复杂度相同。所以，TR⁃CA⁃PM 方法运算量不同的地方是矩阵运算，其复杂度为((+)+ (+))。经Matlab 计算验证，当信号数量+＜34 时，TR⁃CA⁃PM 方法复杂度低于TR⁃CA⁃MUSIC 方法。特别地，当目标数量相对阵元数目越少时，复杂度降低则越明显，在大规模MIMO 阵列中，复杂度的降低极为显著。当目标数量最多（+=-1）时，两种方法复杂度相当。

3 仿真结果

3.1 TR⁃CA⁃MUSIC 方法空间谱仿真

通过Matlab 2016a 仿真分析TR⁃CA⁃MUSIC 方法的相干和非相干目标识别能力。设置互质MIMO 阵列中和分别为3 和4，假设使用全部连续阵元，目标的信噪比SNR=10 dB，信号的快拍数Snapshot=1 000。

如图4 所示，当阵列的发射阵元数=10，接收阵元=11 时，方法成功识别了-1=10 个相干目标。图5显示了=2，=19时算法的识别效果，其中一共识别了18个目标，包含2个相干目标（左2）和16个非相干目标。如图6 所示，当=1，=20 时，阵列不能识别相干目标，但此时是识别目标最多的情况，即可以识别-1=19 个非相干目标。

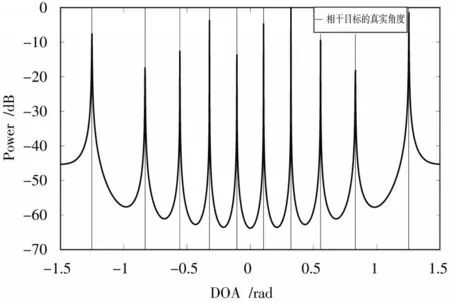
图4 A=10，B=11 时相干目标的MUSIC 谱图

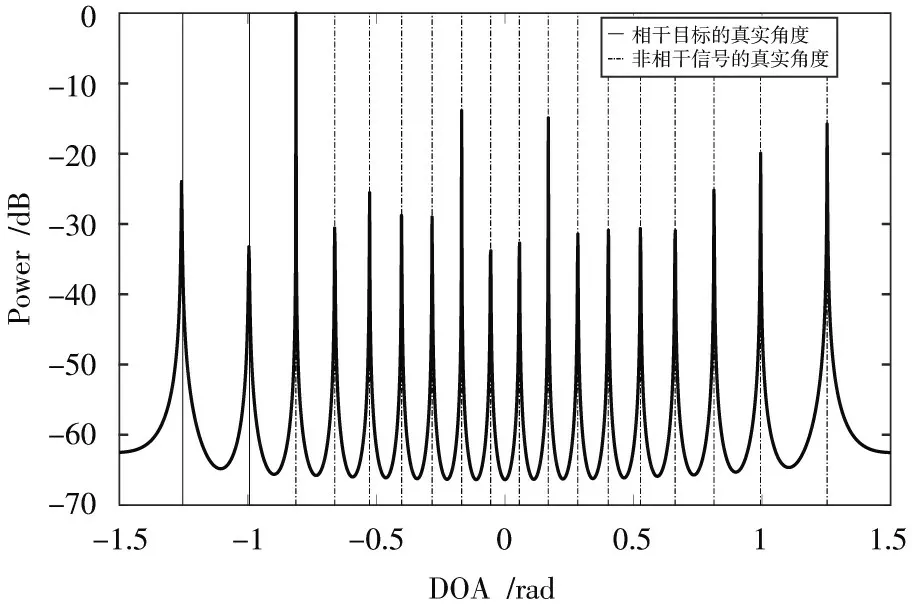
图5 A=2，B=19 时混合目标的MUSIC 谱图

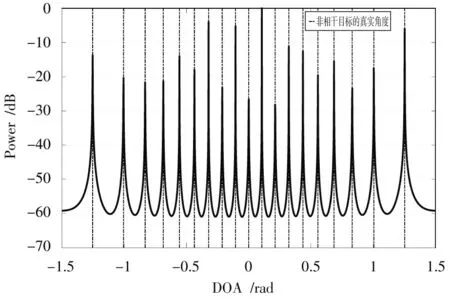
图6 A=1，B=20 时非相干目标的MUSIC 谱图

3.2 TR⁃CA⁃PM 方法空间谱仿真

仿真分析TR⁃CA⁃PM 方法的相干和非相干信号识别能力，保持，，SNR，Snapshot大小不变。

由图7 可看出，=1，=20 时TR⁃CA⁃PM 算法同样能成功分辨出最多19 个非相干目标，所以该方法在整体复杂度较低的情况下仍能达到TR⁃CA⁃MUSIC 方法的识别效果，但该方法的相干目标分辨能力弱于TR⁃CA⁃MUSIC 方法。由图8 可知，TR⁃CA⁃PM 算法仅能识别相干目标的大致角度，因此该方法可用做相干目标角度的快速预处理或者相干目标数量的快速识别。

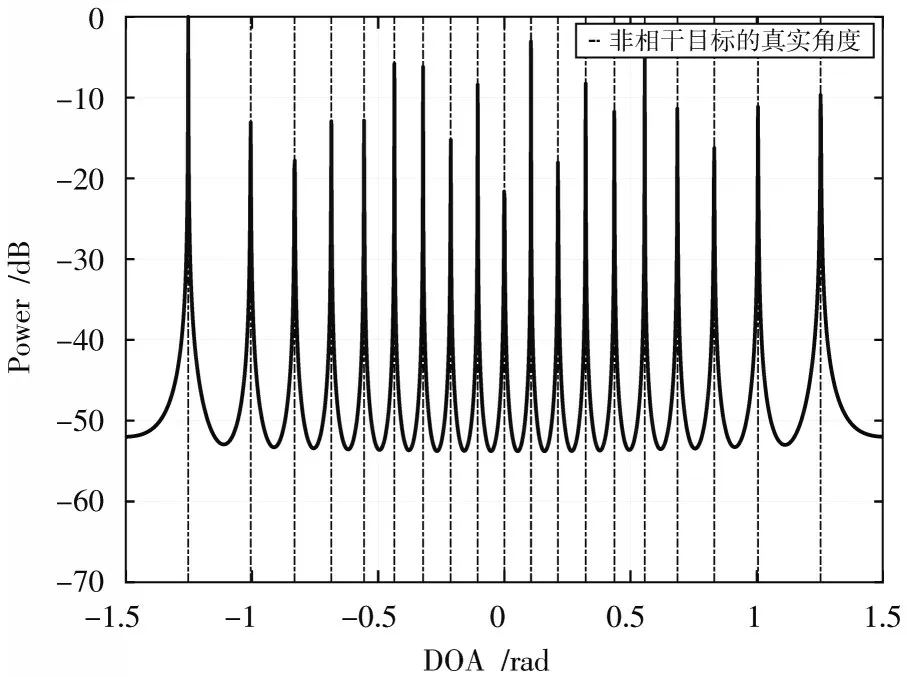
图7 A=1，B=20 时非相干目标的PM 谱图

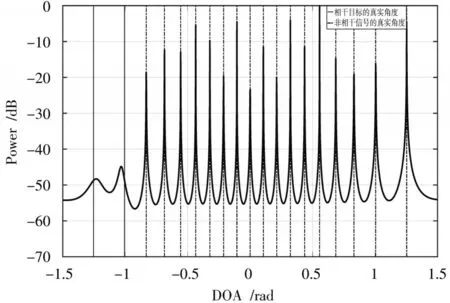
图8 A=2，B=19 时混合目标的PM 谱图

3.3 均方根误差分析

本节的仿真中仿真条件与上节相同，通过对比TR⁃CA⁃MUSIC 方法和TR⁃CA⁃PM 方法的均方根误差（Root Mean Square Error，RMSE）随信噪比的变化情况来衡量两种算法估计非相干目标的性能。均方根误差公式如下：

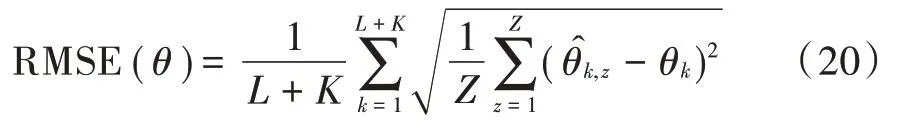
式中：+为相干和非相干目标个数之和；为蒙特卡洛实验次数；θ为第个信号的第次实验的DOA 估计值；θ为信号DOA 实际值。

设置蒙特卡洛次数=1 000，信噪比（SNR）从-11~10 间隔取3，得到两种算法的仿真图如图9 所示。可看出当信噪比和快拍数增大时，两种算法的均方根误差均随之减小。TR⁃CA⁃PM 算法在SNR≥-5 时均方根误差非常接近TR⁃CA⁃MUSIC 方法，因此TR⁃CA⁃PM 算法有着更低的复杂度且具有与TR⁃CA⁃MUSIC 相似的准确率。

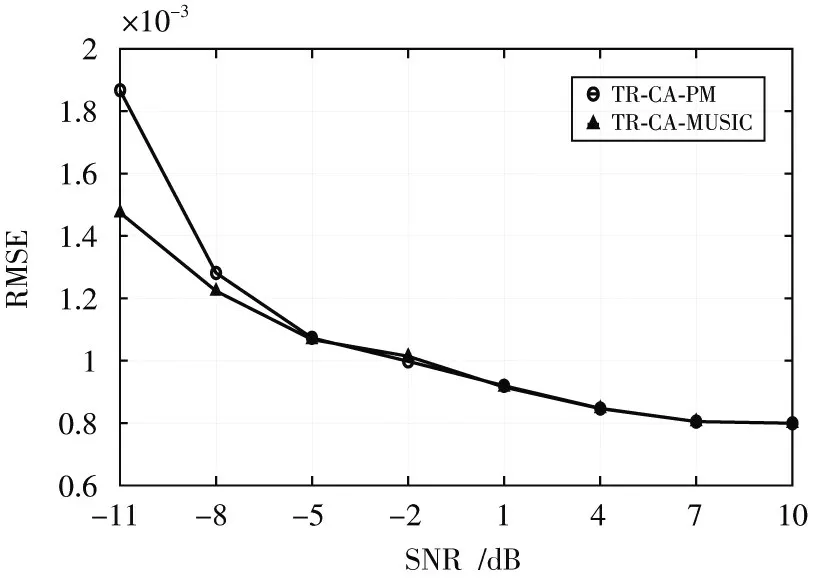
图9 A=10，B=11 时两种方法的RMSE 随SNR 变化图

4 结 语

本文通过对互质MIMO 阵列的和协阵列进行研究，提出了基于MUSIC 的发射/接收和协阵列DOA 估计方法。通过附加另外两种工作频率，延长了和协阵列中连续阵元的数量，提高了阵列的自由度，用2+-1 个互质MIMO 阵元，实现了最多+3-2 个目标的DOA 估计能力，运用到大规模MIMO 阵列中时，自由度的提升更加明显；然后利用数据矩阵重构的方式解相干，实现对相干和非相干目标的DOA 估计；最后针对MUSIC 算法中的特征值分解计算量极大的问题，提出了基于PM 的发射/接收和协阵列DOA 估计方法。在目标为非相干的情况下，两种方法均能有效识别目标，仿真证明其性能相当，在识别混合目标时，后者能以估计相干目标的数量大致估计其角度。此外，两种方法均可根据目标的数量调整发射/接收和协阵元数目，以达到最低的复杂度。