基于非等维状态交互的并行IMM 转移概率自适应算法

张成龙，索继东，麻智雄

（大连海事大学 信息科学技术学院，辽宁 大连 116026）

0 引 言

在目标跟踪领域，对机动目标的跟踪一直是一个重点问题。IMM 算法利用马尔可夫转移概率矩阵及更新的模型概率来实现模型之间的切换，使其准确地匹配目标运动状态，因而在机动目标跟踪领域有广泛的应用。作为一种多模型算法，IMM 算法克服了单一模型下目标运动状态与模型不符所引起的误差，但是若使用的运动模型维度不同，在模型交互时会导致信息丢失，这对目标跟踪是非常不利的。

针对此问题，文献[4]提出一种基于非等维状态的IMM 混合估计方法，通过在交互过程中选取合适的混合策略，来改善非等维状态交互过程中的信息丢失问题。

IMM 算法的转移概率矩阵是影响算法性能的一个关键因素，固定的转移概率矩阵欠缺适配性，会导致目标跟踪精度不足。文献[5⁃6]利用基于模型估计、交互后的估计以及最终融合估计所定义的误差压缩率，对转移概率矩阵进行修正。文献[7]提出一种自适应转移概率交互多模型算法，依据模型似然函数对转移概率进行实时修正，来增强匹配模型的作用，削弱不匹配模型的影响。然而，过多的过去模型信息对转移概率矩阵进行修正，虽然能在一定程度上提高跟踪精度，但存在模型切换响应滞后的问题。因此，文献[9]提出了一种基于自适应转移概率矩阵的并行IMM 算法（ATPM⁃PIMM），将IMM 算法与自适应转移概率矩阵IMM 算法并行运行，综合使用过去模型信息与当前模型信息，能够提高目标模型切换速度与跟踪精度，但ATPM⁃PIMM 算法存在目标模型切换时跟踪误差过大的问题。

为此，本文提出改进的ATPM⁃PIMM 算法，利用文献[4]中的IMM 混合估计方法完善ATPM⁃PIMM 算法的交互过程，在模型混合估计前，利用模型概率和新息来确定最合适的混合估计策略，改善目标模型信息丢失问题，提高模型切换速度，降低模型切换时的峰值误差，提高机动目标的跟踪精度。

1 本文改进的ATPM⁃PIMM 算法

ATPM⁃PIMM 算法本质上是并行运用IMM 算法和自适应转移概率矩阵的IMM 算法，通过转移概率矩阵修正函数，综合利用模型的当前信息和过去信息，相较于只使用过去模型信息修正的自适应IMM 算法，ATPM⁃PIMM 能提高模型切换的响应速度，进而提高平均跟踪精度，但该算法在目标模型发生切换过程中会有较大的峰值误差，特别是在跟踪复杂的机动目标时，频繁的模型切换对目标跟踪尤其不利。

本文提出改进的算法在ATPM⁃PIMM 算法的交互过程中使用基于非等维状态的混合估计方法，在模型交互前，先根据目标模型信息选择合适的混合策略，来改善由于非等维状态交互带来的信息丢失问题，提高模型切换速度，降低模型切换时的峰值误差，从而提高对复杂机动目标的跟踪性能。

1.1 ATPM⁃PIMM 算法的转移概率修正函数

ATPM⁃PIMM 算法通过转移概率修正函数，自适应地引入模型的当前信息与过去信息。在时刻，模型的转移概率修正函数为：

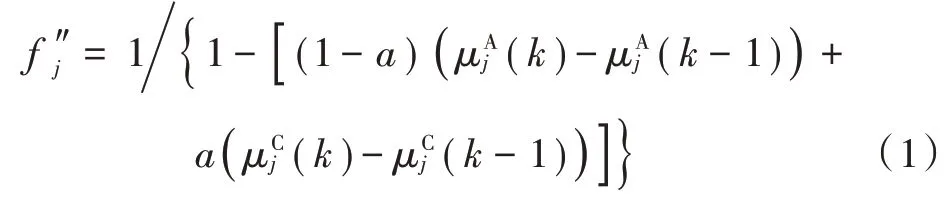
式中：和分别表示模型在标准的IMM 算法和转移概率自适应IMM 算法中的模型概率；表示切换系数。

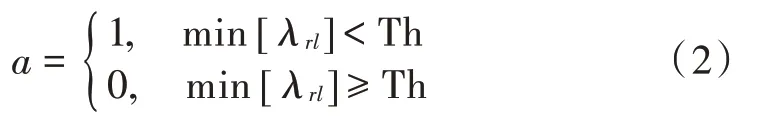
Th 表示设置的模型切换阈值，λ表示模型间的似然比：

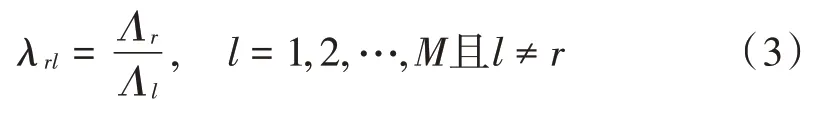
模型表示匹配模型。由于IMM 算法中的似然函数表示系统模型与实际模型的匹配程度，因此利用模型间的似然比能够有效地判断系统模型是否发生切换。设模型切换阈值为Th，当Th＞λ时，模型发生切换，引入当前模型信息；反之，则模型未发生切换，使用过去模型信息。

修正后的转移概率表示为：

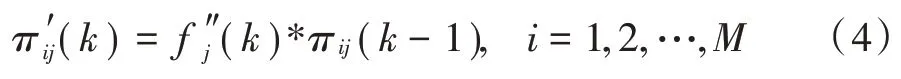
对其进行归一化，就得到新的转移概率：

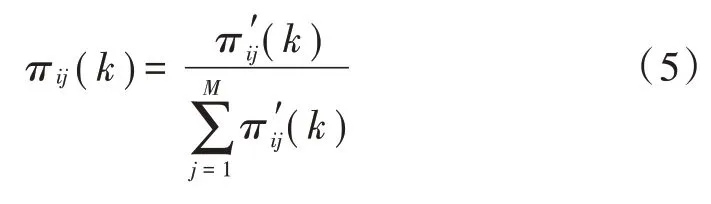
1.2 交互过程中基于非等维状态的IMM 混合估计

在IMM 算法的交互过程中，若使用的运动模型维度不同，会导致目标信息丢失现象。所以需要选择合适的模型混合估计策略：对于低维模型的状态交互，可以直接舍弃高维模型的额外分量，直接进行混合估计；而对于高维模型的状态交互，则需要先对低维模型按某种方式进行扩维后，再进行混合估计。

文献[10]提出一种简单的扩维方法，对低维状态采用零均值和协方差进行扩维，但会导致有偏估计；文献[11]提出一种无偏的方法，利用高维模型中“额外”的分量对低维模型进行扩维；文献[12]提出的方法考虑到了系统的切换，其对高维模型的“额外”分量采用均匀分布进行描述，使被扩维的低维模型能够尽可能地反映系统的模式切换；文献[4]提出一种综合的非等维混合估计方法，将上述三种方法纳入统一框架下，以确定合适的混合估计策略。将上述四种方法分别记为A1、A2、A3和A4。

A1、A2、A3 是基于不同的假设设计的，A1 假设当前系统模型为低维模型，A2 假设当前系统模型为高维模型，A3 则假设系统模型在跳变中，在这些假设成立的情况下，使用这些方法确实能提高目标跟踪精度。所以A4 将A1、A2、A3 纳入同一框架下，引入“切换”的概念，根据模型概率和新息，尽可能地确定目标模型的运动状态，以选择最合适的估计策略。

假设在一个双模型系统中，运动模型1 的状态向量维度大于模型2，且模型2 的状态向量包含于模型1，设模型1 中的额外分量为()。此系统共有4 种运动状态：，，和。如果目标真实状态为，则匹配模型为高维模型，A2 方法为最优选择；同样地，当目标的真实状态为时，A1 方法为最优选择；对于“切换”状态，此过程为高维模型向低维模型的切换，在此过程中()应置为0，因此其最优选择同样为A1；当目标状态为时，则()可能在取值区间跳变，故采用A3 的均匀分布假设。

在上述运动状态中，和可以通过模型概率μ()确定，状态可由一个机动检测器确定，检验统计量计算公式为：

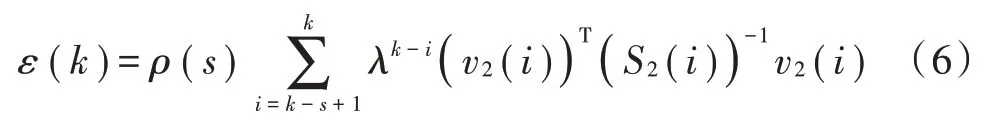
式中：()= (1-) (1-λ)，0 ＜＜1 为衰减因子，()和()分别为模型2 的新息及其协方差，代表滑窗长度，[-+1,]为滑窗检测区间。设检测阈值为()，当检验统计量大于阈值时，说明模型发生切换，则使用A3 重新估计滑窗区间[-+1,]内的目标状态。当检验统计量低于阈值时，则直接利用模型概率确定目标状态，即当()＞()时，采用A2 进行混合估计；否则，采用A1 方法。

上述为A4 方法的描述，其可以利用量测数据的后验信息校正目标状态，从而提高模型的切换速度，抑制因模型切换造成的跟踪误差增加，以降低峰值误差。

1.3 本文算法流程

基于A4 算法对ATPM⁃PIMM 算法中的交互过程进行改进，在进行各模型间的交互混合之前，先利用A4 算法选择合适的混合估计策略。

改进的ATPM⁃PIMM 算法流程如下：

1）输入交互

利用式（6）计算检验统计量来确定模型运动状态，设定检测阈值()，当检验统计量大于检测阈值时，说明模型切换发生，利用A3 进行混合估计；当检验统计量低于阈值时，则利用模型概率确定使用的估计算法，当()＞()时，采用A2 算法；否则，采用A1 算法。

对高维模型进行混合估计时，根据上述确定的混合估计策略对低维模型进行扩维，然后再进行混合估计；对于低维模型则直接舍弃高维模型中的“额外”分量直接进行混合估计。由于改进的ATPM⁃PIMM 算法基于并行IMM 算法的框架，所以模型的混合估计公式为：

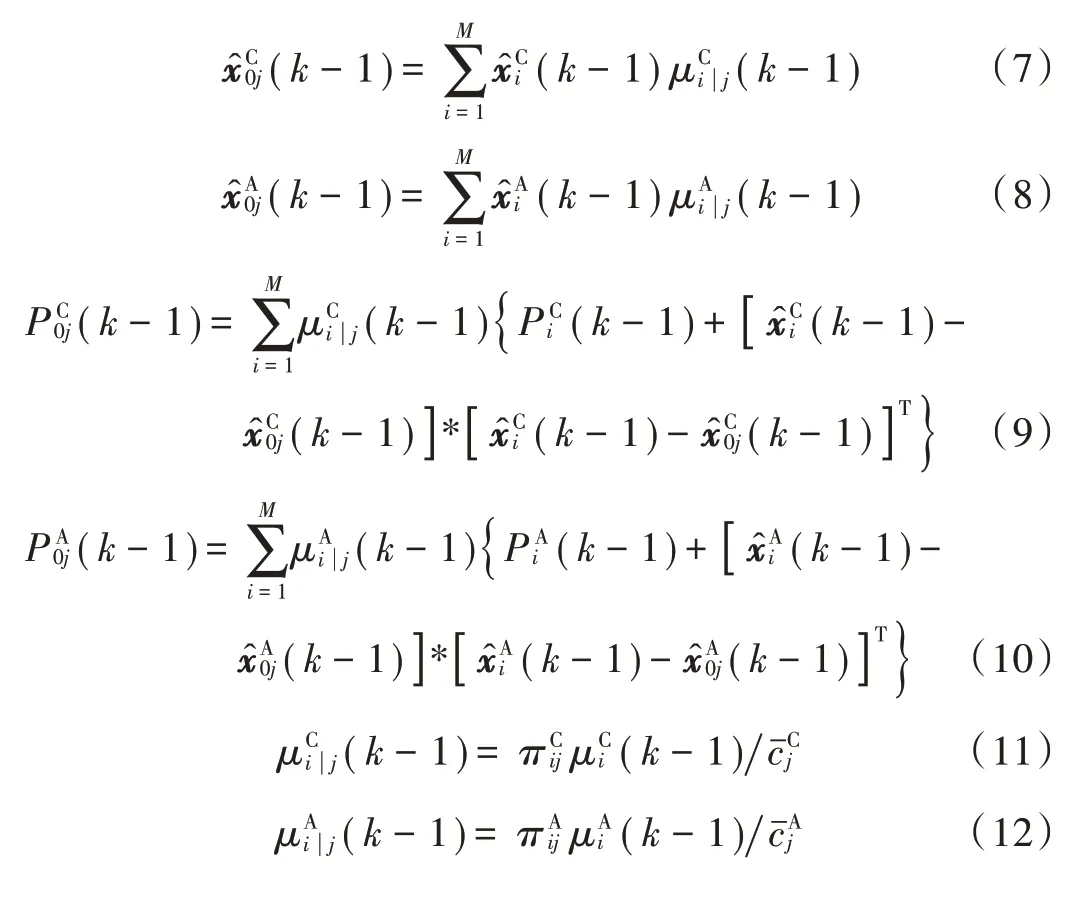
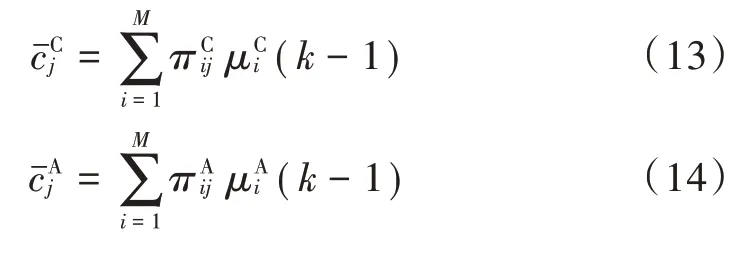
式中：上标A 表示转移概率自适应的IMM 算法中的变量；上标C 表示标准的IMM 算法中的变量。

2）并行滤波

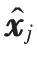
3）模型概率更新

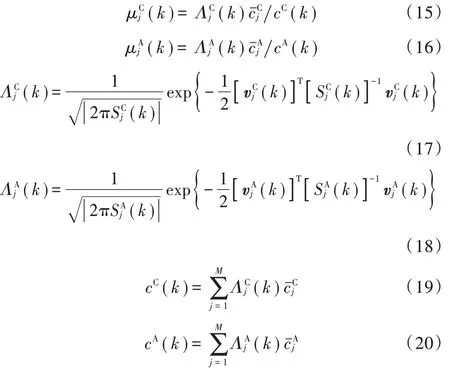
4）信息融合

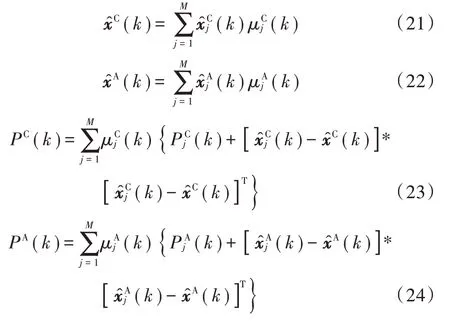
5）转移概率更新

利用式（1）~式（5）对并行运行的自适应IMM 算法中的转移概率矩阵进行自适应处理，而标准的IMM 算法中的转移概率保持不变。

2 仿真分析

模型集由CV 模型和CT 模型组成，两种模型的状态向量分别为：

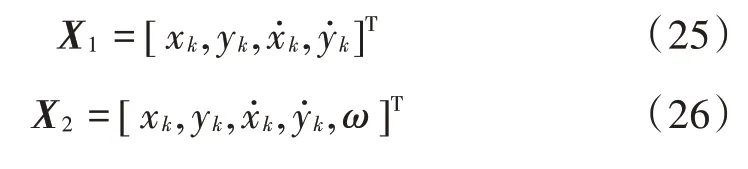
式中为转弯率。CV 模型的过程噪声参数为0.001，CT模型的过程噪声参数为0.015，观测噪声协方差矩阵参数为0.1。目标初始状态为[0 m；0 m；1 m/s；0 m/s]，在0~4 s 内做匀速直线运动，在4.1~9 s 内做1 rad/s 的匀速转弯运动，在9.1~11 s 内做匀速直线运动，在11.1~16 s内做-1 rad/s 的匀速转弯运动，在16.1~20 s 内做匀速直线运动。目标的运动轨迹如图1 所示。

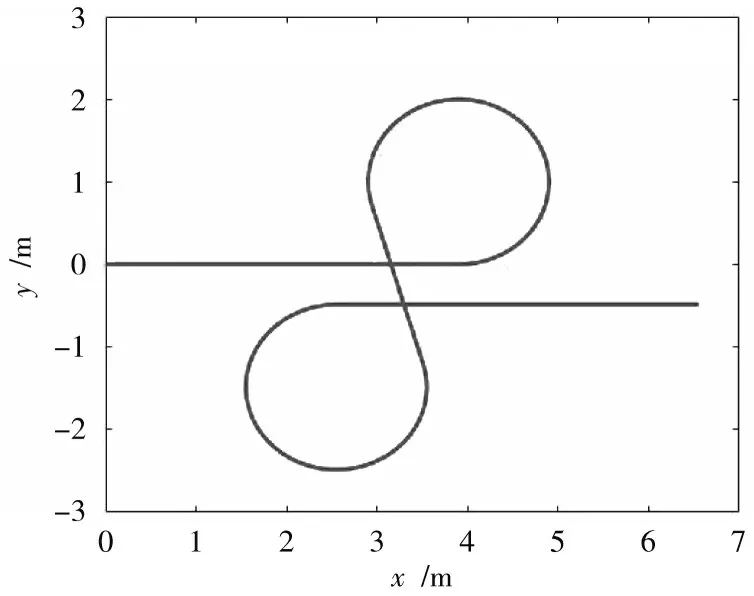
图1 目标真实运动轨迹

采样时间设为0.1 s，交互多模型的初始模型概率为[0.5 0.5]，转移概率矩阵设为[0.95 0.05；0.05 0.95]，根据文献[9]设模型切换阈值Th 为0.9，在改进的ATPM⁃PIMM 算法中，设检测阈值()=15，进行200 次蒙特卡洛仿真验证，用ATPM⁃PIMM 算法与改进的ATPM⁃PIMM算法分别对目标进行跟踪，得到的结果如图2~图5所示。

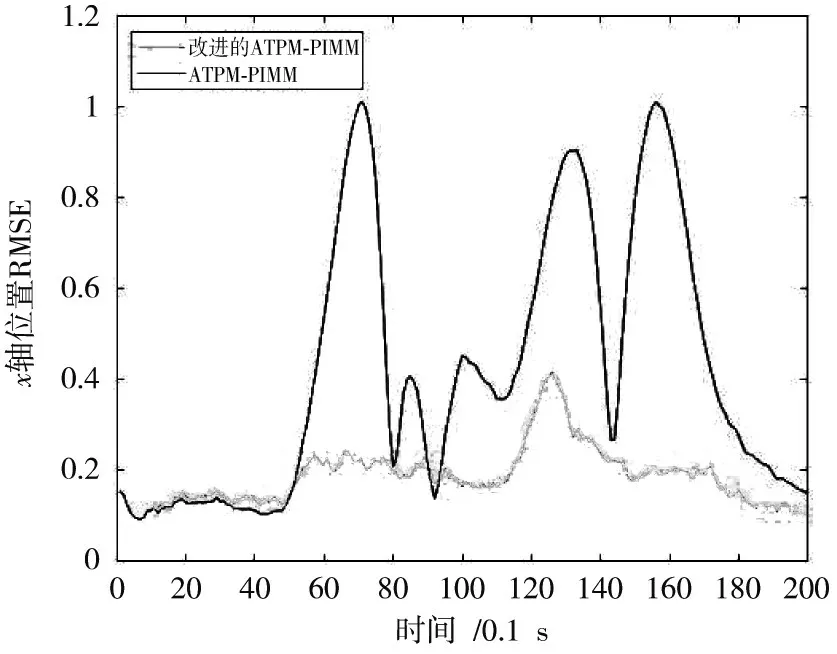
图2 x 方向位置估计值均方根误差

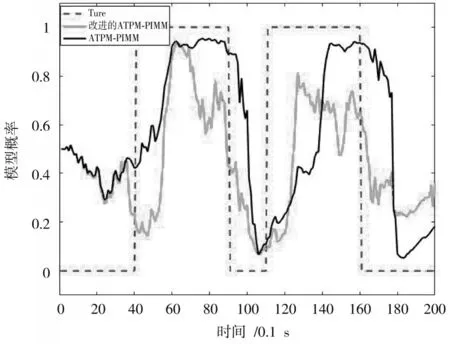
图5 CT 模型概率图

从误差图可以看出：在开始阶段，两算法的跟踪精度相差不大，改进的ATPM⁃PIMM 算法的跟踪误差甚至略有提高；但在之后的模型切换阶段，ATPM⁃PIMM 算法的峰值误差明显，而改进的ATPM⁃PIMM 算法能有效地降低由于模型切换带来的峰值误差，保证良好的跟踪精度。从模型概率图也可以看出，改进的ATPM⁃PIMM算法的模型切换速度要快于ATPM⁃PIMM 算法。

综上所述，改进的ATPM⁃PIMM 算法的性能优于ATPM⁃PIMM 算法，能够满足对机动目标跟踪的需要。

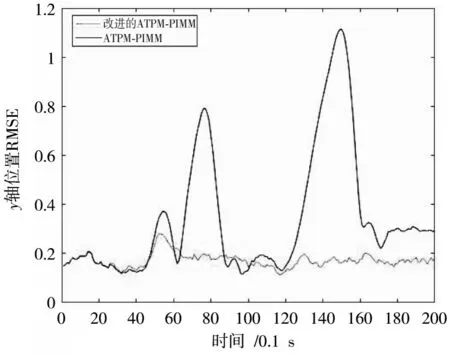
图3 y 方向位置估计值均方根误差

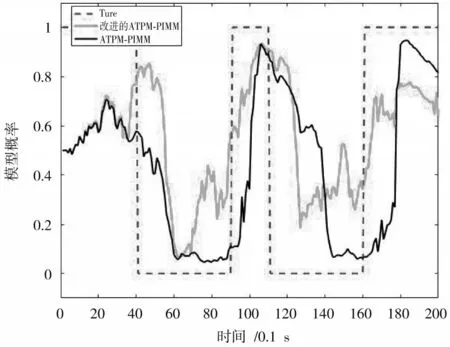
图4 CV 模型概率图

3 结 语

实际跟踪目标的运动状态是多变的，目标模型的频繁切换会对目标跟踪造成不利影响，为了更好地完成对目标的跟踪，本文利用基于非等维状态混合估计的方法对ATPM⁃PIMM 算法进行改进，提出并仿真验证了改进的ATPM⁃PIMM 算法。该算法与基本的ATPM⁃PIMM 算法相比，改善了模型的切换速度，提高了跟踪精度。由于影响算法性能的阈值参数是根据先验信息确定的，所以在今后的研究中，还需在参数()与λ寻优上加以改善，对参数进行自适应化处理。