基于遗传算法的异构无线传感器网络分簇算法

刘 涛，庞 博

（西安科技大学 通信与信息工程学院，陕西 西安 710054）

0 引 言

异构无线传感器网络（Heterogeneous Wireless Sensor Networks，HWSNs）是由许多初始能量不同的传感器节点组成，这些节点被随机分配到目标区域，通过感知周围物理量信号来获取监测区域的相关数据信息，节点之间通过无线通信进行数据传输。实际应用中，被广泛部署在无人可达的恶劣环境中，用于监测周围环境的变化情况，例如监测山体滑坡、地震、泥石流预警等。研究发现，传感器节点的能量消耗主要来源于无线通信模块。因此，如何降低数据传输过程中节点之间的无线通信能耗，找到更优的路由算法，已成为异构传感器网络的重要研究方向之一。

SEP算法是在LEACH 算法的基础上，针对WSN 节点初始能量不同进行改进的分簇算法。将节点分为高级节点和普通节点，两种节点分别采用不同的阈值进行簇头选举。TSEP是在SEP 算法的基础上，增加了超级节点。在TSEP 算法中超级节点、高级节点、普通节点因初始能量不同，具有不同的概率值当选簇头节点。Z⁃SEP是Faisal 等人提出的一种基于区域划分的HWSNs 分簇算法，能够有效延长网络生存时间，但Z⁃SEP 算法有很大的局限性，节点分布位置指定无法随机部署，只有高级节点作为簇头。

为进一步降低HWSNs 数据传输过程中的无线通信能耗，本文在SEP 算法基础上提出了一种基于遗传算法改进的HWSNs 分簇算法。分析传感器节点的剩余能量、节点分布位置以及节点的邻居节点密度因素后，通过遗传算法寻优，选举出每轮最佳数目的最优簇头集，同时提出一种簇头更新策略，降低周期性分簇造成的能量损失。

1 系统模型

1.1 网络模型

本文对部署在区域范围内的无线传感器网络做如下假设：

1）传感器节点分为高级节点和普通节点，高级节点的初始能量高于普通节点。除此之外，两种节点的存储、处理、传输能力一样，无任何差别。

2）每个节点都具有唯一ID 编号，随机部署在监测区域内。

3）节点部署完成后，整个网络处于静态，节点不可移动。

4）基站节点具有强大的计算能力和处理能力，并且供电为有源方式。

5）传感器节点具有GPS 定位功能。

1.2 能量模型

一阶无线电模型是众多研究WSNs 能量消耗的采用对象，因此，本文计算节点间数据通信消耗采用的能量损失公式也将基于此模型。模型具体示意图如图1所示。

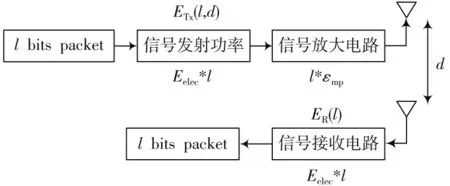
图1 一阶无线电能耗模型

该模型工作在两种模式下，自由空间模型和多路径衰落模型。传感器节点发送bit 数据，传输距离长度，消耗的能量如式（1）所示。

式中：，，分别代表发射机和接收机使用的功率、自由空间模型的功率放大器系数和多径衰落模型的功率放大器系数。代表距离阈值，计算公式为：

接收机接收发射机传输的bit 数据信息，消耗的能量为：

2 簇头选举

大多数分簇路由算法中，簇头的选择是基于概率方程，例如，LEACH、SEP、TSEP 算法等。此类方法有可能选出剩余能量较低的节点作为簇头，影响整个网络生命周期。为选举出更优秀的簇头节点，本文改进了簇头选举的方式，不再是用概率方程随机选取，而是使用遗传算法选举簇头。

2.1 遗传编码的选择

常见的遗传算法编码方式有：二进制编码、十进制编码、实数编码、浮点数编码等，其中，使用最多的是二进制编码和实数编码。二进制编码使用比较简单，易于交叉、变异等遗传操作的实现，但局部搜索能力比较差。实数编码相比二进制编码，能够兼顾搜索效率和准确性。因此，本文采用实数编码方式对传感器节点进行编码。

2.2 适应度函数的设计

适应度函数要对种群中的节点做综合性的评估判断，适应度函数设计的好坏，直接决定着选举出的簇头集的优劣程度。本文在簇头选举过程中综合考虑了节点剩余能量、节点分布位置以及邻居节点密度三个因素，计算所有节点的适应度函数值，选举出适应度函数值最优的节点作为簇头。

节点的剩余能量是网络中选择簇头节点首要考虑的因素。剩余能量越大，被选为簇头节点的概率越大。如式（4）所示，E表示节点当前的剩余能量，和分别代表当前轮数下网络中节点剩余能量的最小值和最大值。f能体现出节点剩余能量在当前网络中所处的能量等级，可以看出，节点剩余能量越大，能量等级越高，被选中簇头节点的概率越大。

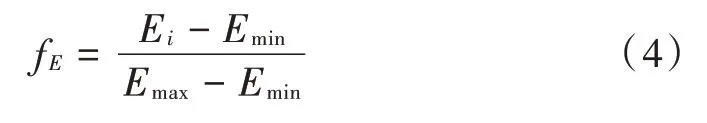
节点所处的位置直接影响节点与簇头节点、基站中心的通信，距离目标节点越远，节点需要消耗的通信能量越多。本文衡量节点分布位置的计算公式为：

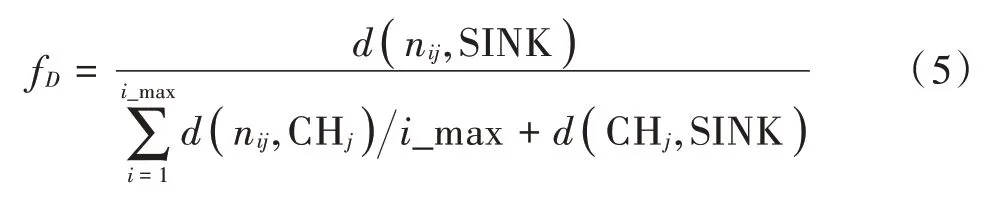
式中：f代表节点分布位置因子；( CH,SINK )表示簇头节点与基站SINK之间的距离；(n,CH)表示集群内非簇头节点到所属簇头节点之间的距离；(n,SINK)表示非簇头节点到基站SINK 的距离。非簇头节点到所属簇头节点距离(n,CH)越小，簇头节点距离基站( CH,SINK )越小，节点需要的通信距离越短，节点所处的位置更优。初始情况下，所有节点作为非簇头节点，基站被认为是网络中的唯一簇头。

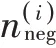
适应度函数计算公式如下：

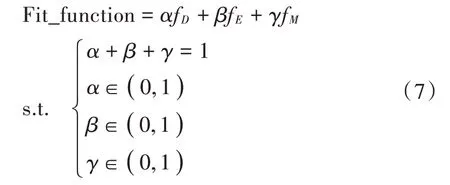
式中：，和分别代表节点分布位置因子、能量因子、邻居节点密度因子的权重系数，取值在（0，1）区间内，权重系数取值之和等于1。

2.3 选择操作

遗传算法中选择操作能够保证选出适应度函数值最优的节点遗传给下一代，本文采用精英保留策略和轮盘赌相结合的选择方式。利用精英保留策略选择出优秀的个体直接保留到下一代，其他个体利用轮盘赌方式进入下一代，计算公式为：

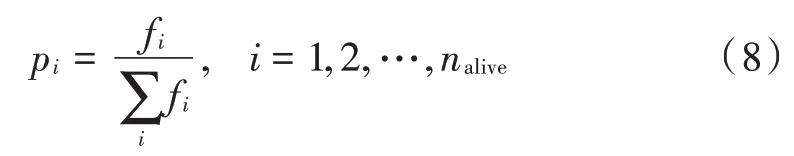
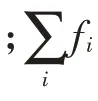
分簇的大小和个数影响WSNs 的整体性能。分簇数目较少，簇内通信能耗加大；分簇数目较多，无法起到分簇作用。为了得到合适的簇头个数，本文根据式（9）计算每轮需要选举的簇头节点个数。

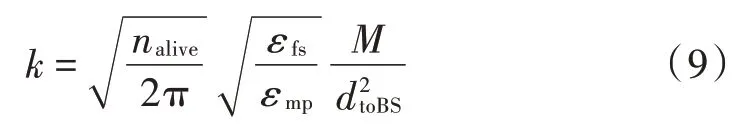
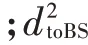
2.4 更新策略

为均衡整个HWSNs 中节点能耗，避免某些节点能量消耗过快、过早死亡，大量分簇算法在进行簇头选举时，避免单个节点多次当选簇头，当选过簇头的节点不再当选，达到每个节点都至少有一次当选簇头节点的机会。经典的LEACH 算法采取该方法，有效地延长了网络的生命周期，起到了均衡网络的作用。但实际情况中，LEACH 算法并没有使得传感器网络的生命周期延长的太久，反而每一轮的簇群建立，簇头节点与普通节点之间进行无线通信都会消耗节点的剩余能量。针对此问题，考虑簇头节点的剩余能量、所属簇群能量以及整个网络能量的消耗情况，本文提出一种簇头节点更新策略，当簇群处于稳定阶段，在下一轮簇头选举之前，计算每个簇群的平均能量和网络中存活节点的剩余能量，判断更新策略条件是否满足。

簇头节点所属簇群的平均能量为：

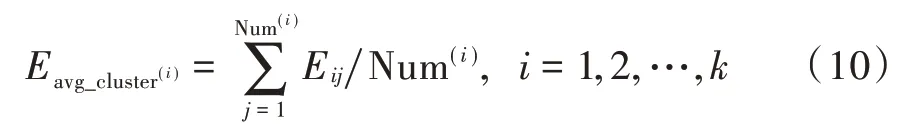
式中：为簇头节点代表的簇群平均能量；Num表示簇头节点代表的簇群中存活节点的个数；E表示簇头节点代表的簇群中第个成员节点；代表簇头节点的最大个数。

网络中存活节点的平均能量为：

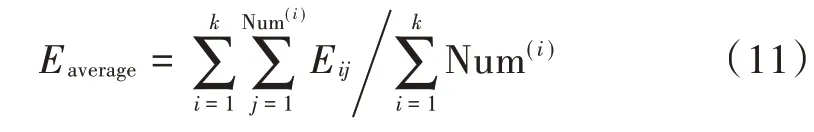
式中：代表网络中存活节点的平均能量；表示网络中簇头节点的个数。

更新策略具体流程如下：

步骤1：根据式（10），式（11）分别计算每个簇的平均节点能量和整个网络存活节点的平均能量。

步骤2：条件Ⅰ）簇头节点剩余能量大于所属簇群的平均能量；条件Ⅱ）簇头节点剩余能量大于当前轮次整个网络存活节点的平均能量。统计同时满足条件Ⅰ）、条件Ⅱ）的簇头节点获得连任，继续当选下一轮的簇头节点，所属簇群保持不变，无需建簇。其余节点重新计算适应度函数值，选举下一轮中其余的簇头节点。

簇头更新策略流程图如图2 所示。

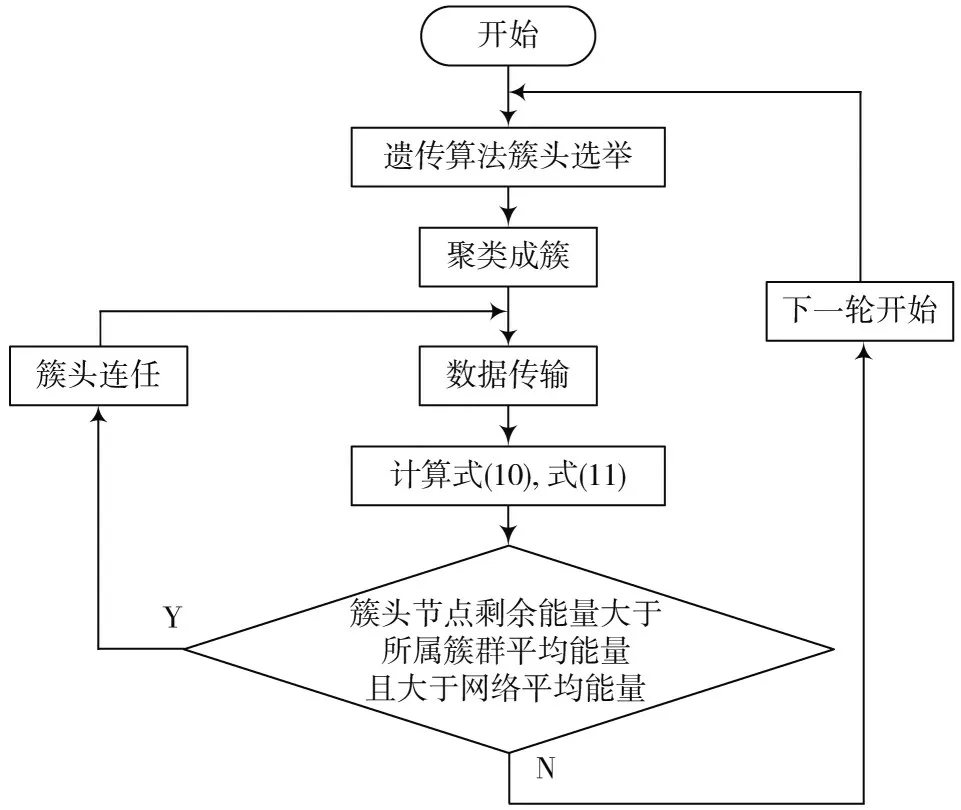
图2 簇头更新流程图

2.5 算法流程图

改进的无线传感器网络分簇算法流程图如图3所示。

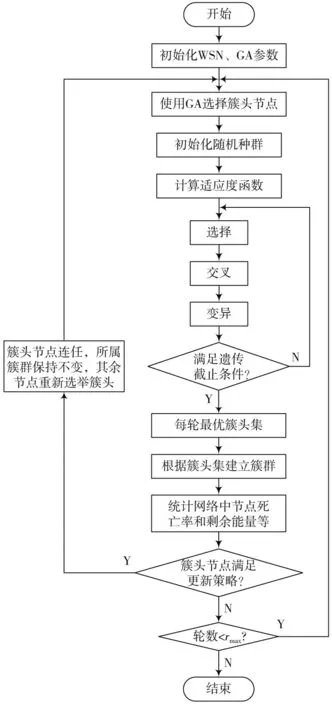
图3 改进算法流程图

3 仿真实验与分析

本文在Windows 平台下，使用Matlab R2012a 作为仿真实验环境，将本文提出的算法与SEP 算法、带有10%高级节点的LEACH 算法以及TSEP 算法进行对比实验分析。实验参数如表1 所示。

表1 仿真实验参数

3.1 100 m×100 m 网络部署区域仿真分析

在100 m×100 m 正方形网络部署区域下，基站节点坐标为（50 m，50 m）。图4 为100 m×100 m 网络区域下四种算法死亡节点随时间变化的对比图。由图可知，大约在1 500 轮左右，本文提出的算法第一死亡节点出现，此时SEP 算法90%节点已经死亡，LEACH（=0.1，=1）算法80%节点已经死亡，表现最好的TSEP 算法大约也有5、6个节点出现死亡。SEP算法、LEACH（=0.1，=1）算法以及TSEP 算法全部节点都死亡时，本文提出的算法大约只有80%节点死亡。可见相比其他三种方法，本文算法在延长网络生命周期方面有更好的表现。

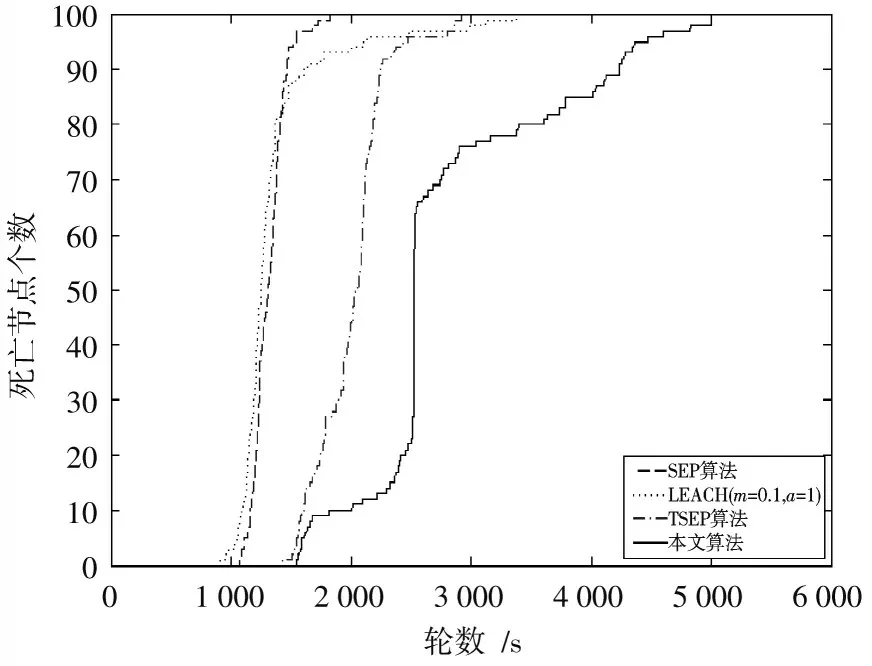
图4 100 m×100 m 区域网络死亡节点个数

表2 是100 m×100 m 区域下四种算法的网络寿命数据。表中分别比较了四种算法第一死亡节点、10%死亡节点、半数死亡节点和全部节点死亡出现的轮数。

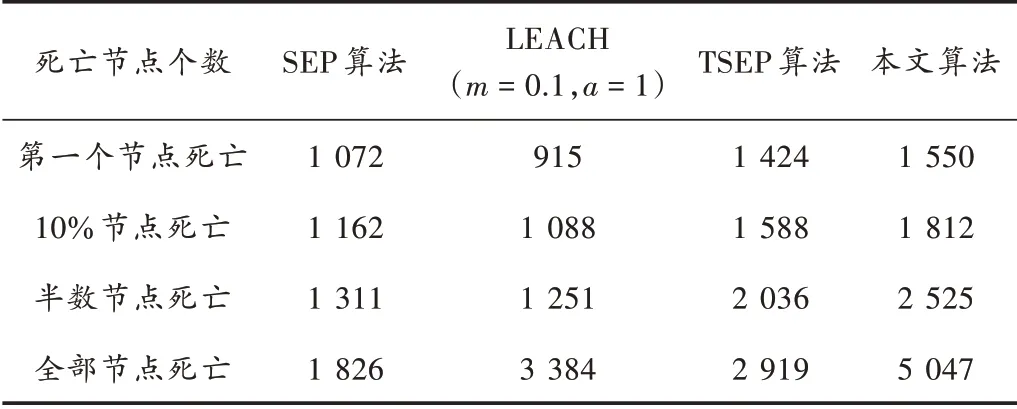
表2 100 m×100 m 区域的网络寿命数据

从表2 可以直观看出：与SEP、LEACH（=0.1，= 1）算法以及TSEP 算法相比，本文提出的算法在第一节点死亡处的寿命分别提高了44.59%，69.4%和8.85%；半数节点死亡处的寿命分别提高了92.6%，101%和24%；全部节点死亡的寿命分别提高了174%，47.78%和71.33%。

如图5 所示，比较100 m×100 m 区域下四种算法网络剩余能量变化情况。大概在1 200 轮之前，SEP 和LEACH（=0.1，=1）算法两者网络中的剩余能量几乎没什么差距，1 200 轮之后LEACH（=0.1，=1）算法的网络剩余能量开始明显高于SEP 算法。本文算法从300 轮以后，网络中的剩余能量一直高于另外三种算法，5 000轮左右网络总能量才基本耗尽，四种算法中本文算法节点能量利用率更高。

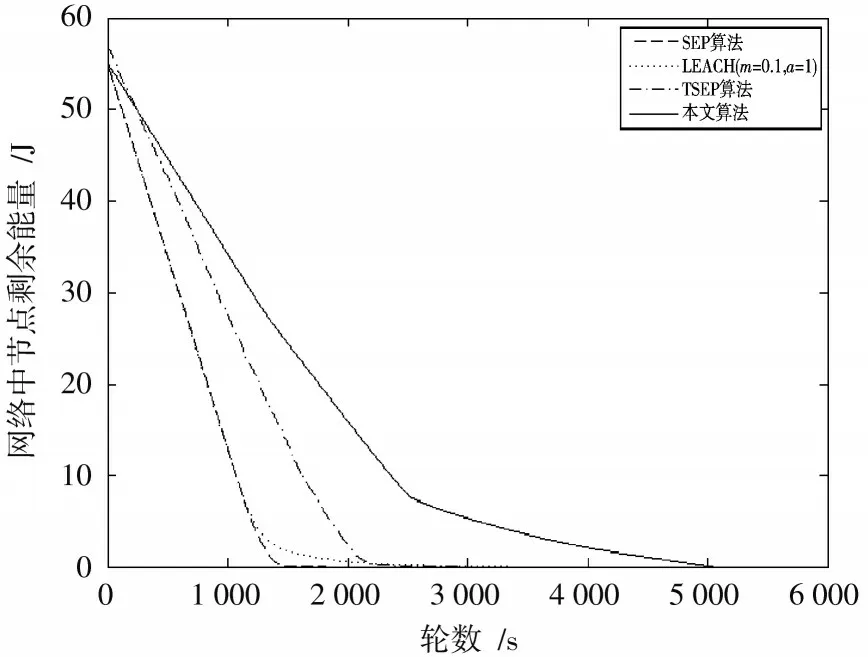
图5 100 m×100 m 区域的网络剩余能量

3.2 200 m×200 m 网络部署区域仿真分析

在200 m×200 m 区域下，基站节点坐标为（50 m，50 m），其他仿真实验参数跟100 m×100 m 区域采用的参数一样。

图6 为200 m×200 m 区域四种算法死亡节点的对比图。图中四种算法第一死亡节点出现的轮数都明显早于100 m×100 m 正方形区域下的相同算法，但第一死亡节点出现的轮数顺序并未改变，依然是LEACH（=0.1，=1）算法最早，本文算法最晚。相同轮数下，本文算法死亡节点个数要远少于SEP、LEACH（=0.1，=1）和TSEP 算法。

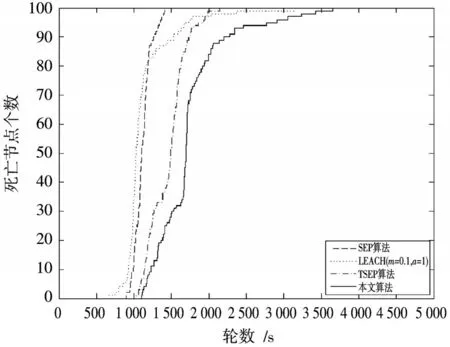
图6 200 m×200 m 区域网络死亡节点个数

表3 是200 m×200 m 区域下四种算法的网络寿命数据。由表3 可知：与SEP、LEACH（=0.1，=1）和TSEP 算法相比，本文算法在第一个节点死亡处的寿命分别提高了23.71%，65.31% 和6.9%；半数节点死亡处的寿命分别提高了54.46%，64.66%和14.1%；全部节点死亡的寿命分别提高了159%，16.46% 和70.21%。

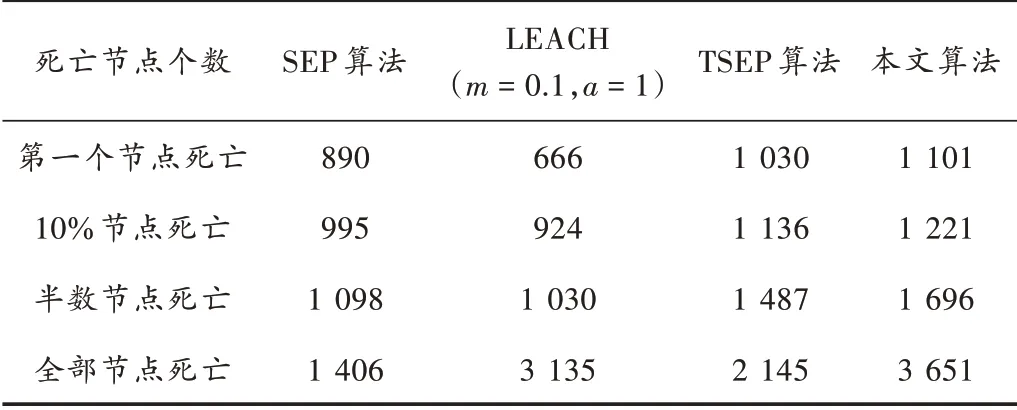
表3 200 m×200 m 区域的网络寿命数据

图7 为200 m×200 m 区域四种算法的网络剩余能量对比图。相比图5，图7 中四种算法消耗的能量更快，同一时间下网络剩余能量更少，这是因为网络区域覆盖由100 m×100 m 变为200 m×200 m，而网络节点个数、总能量不变，通信传输距离变远导致节点能量消耗更快。但图5 和图7 总的网络节点剩余能量变化趋势显示，本文提出的算法总体上要优于另外三种算法。

图7 200 m×200 m 区域的网络剩余能量

4 结 语

为了延长异构无线传感器网络生命周期，本文对簇头选举进行优化，考虑节点的剩余能量、分布位置以及邻居节点密度因素，通过遗传算法选举出每轮最优簇头集进行分簇聚类；同时考虑到频繁进行簇头选举、建簇操作会浪费能量损失，提出一种簇头更新策略，允许能量充足、满足条件的簇头节点继续当选簇头。仿真结果表明，无论是100 m×100 m 网络区域还是200 m×200 m网络区域，本文提出的算法在网络生存周期、能量损耗方 面 明 显 优 于SEP、LEACH（=0.1，=1）和TSEP算法。