剪叉式高空作业平台举升机构参数匹配研究*

2022-02-28刘吉超张伟康郑自冲李怀义刘治军

机电工程 2022年2期

关键词：推杆油缸液压

刘吉超,张伟康,郑自冲,李怀义,刘治军,常奎

(1.江苏汇智高端工程机械创新中心有限公司,江苏徐州 221000;2.徐工消防安全装备有限公司,江苏徐州 221100)

0 引言

剪叉式高空作业平台[1,2](SAWP)利用液压油缸[3,4]驱动剪叉机构的伸缩,实现对平台的升降控制,以此满足操作者对不同高度的作业需求。

但是液压油缸存在液压油泄漏及能量利用率低的弊端,使其难以满足未来电子厂、超市等场所对SAWP绿色节能的作业要求[5]。近年来,得益于电推杆[6](又称电动线性执行器)的发展,为解决SAWP这一问题提供了可行途径。

与常用的液压油缸不同,电推杆在驱动举升机构时,它将电机的旋转运动通过丝杆转换成直线运动,以此控制油缸的伸缩动作。由于整个过程无液压油的介入,不存在液压油泄漏的情况,且其能量利用率更高。

然而,电推杆的刚性特点使其无法通过溢流阀适应举升过程的负载变化,这对电推杆驱动的举升机构动力参数匹配提出了更高的要求。

目前,在SAWP举升机构动力参数匹配的研究方面,研究者们主要关注的是对剪叉臂结构和油缸铰点位置的相关研究[7-11]。其中,牛文欢等人[8]在分析了斜置式和水平式铰点受力特点的基础上,得出了斜置式安装位置更符合举升油缸受力分配的结论。刘伟[9]建立了举升油缸的受力模型,利用人工智能算法对油缸安装铰点进行了优化,并利用ANSYS软件对其优化结果进行了验证。龚建球[10]以减少油缸最大推力为目标,利用梯度下降算法对油缸安装位置进行了优化,并利用AMESim软件对铰点受力过程进行了仿真验证。HE S等人[11]针对举升油缸提出了基于虚功原理的油缸动力参数匹配方法,使匹配后的油缸峰值推力和稳态推力分别减小了12%和20%。

综上所述,现有举升机构动力参数匹配方法主要聚焦举升油缸,鲜有对电推杆驱动的举升机构动力参数进行匹配的研究。

为此,笔者以某型6 m SAWP为载体,围绕其举升机构的电动化问题,通过建立举升机构模型,对电推杆铰点位置进行优化,以及对机构动力参数进行匹配验证,开展对SAWP举升机构的电动参数匹配研究。

1 举升机构建模

笔者以某型6 m SAWP的剪叉机构为研究对象,采用空间位置分析法[12]对剪叉机构进行建模。

6 m SAWP的剪叉机构结构原理如图1所示。

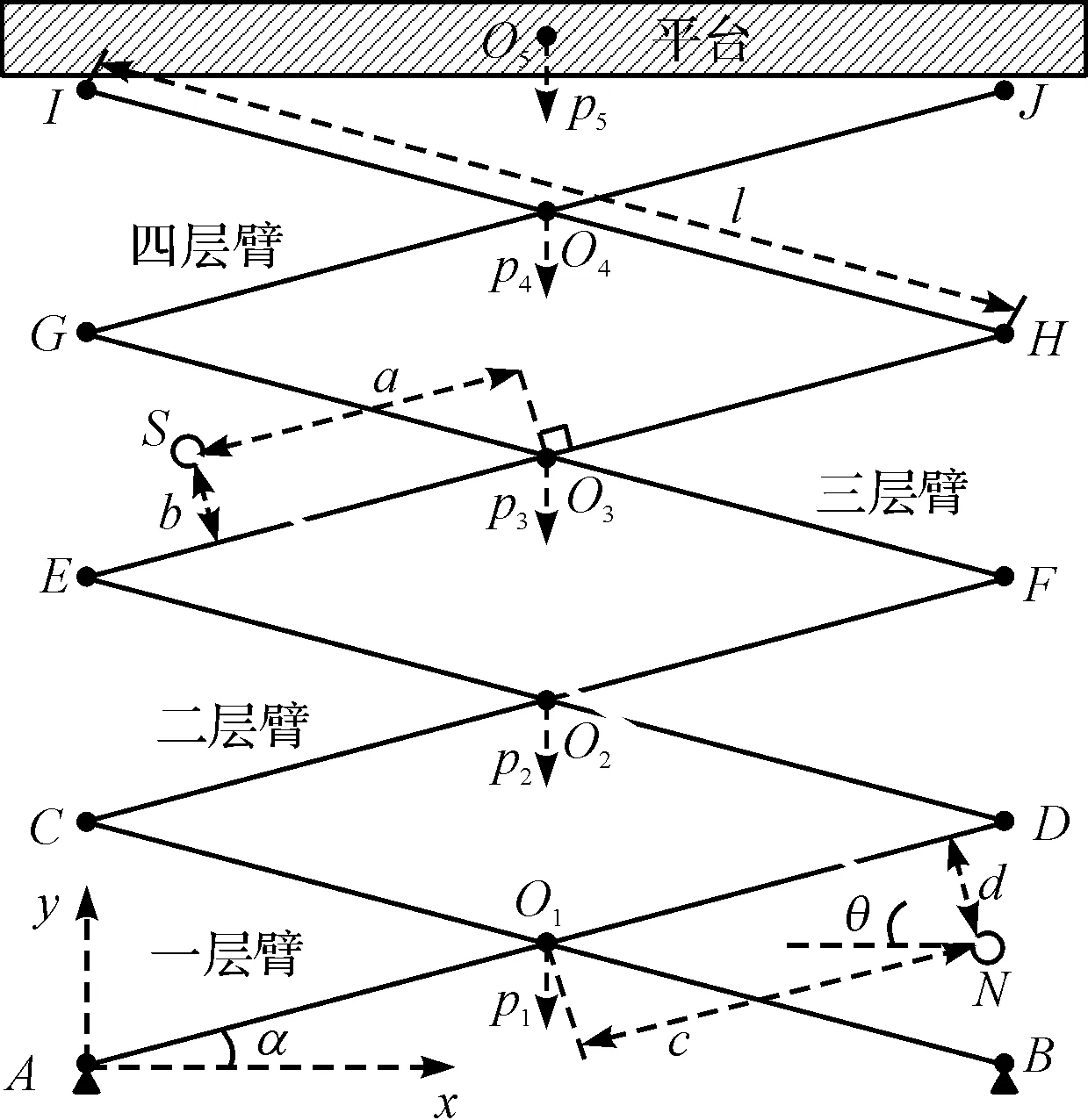
图1 SAWP剪叉机构原理

在图1中:SN表示举升机构的电推杆,点A～点J为铰点,点A和点B分别与车辆底盘机械连接;点Oi为4层剪叉臂的质心,i=1,2,3,4,均与各层剪叉臂的几何中心点重合,点O5为平台质心。

该举升机构电推杆的总成结构如图2所示。

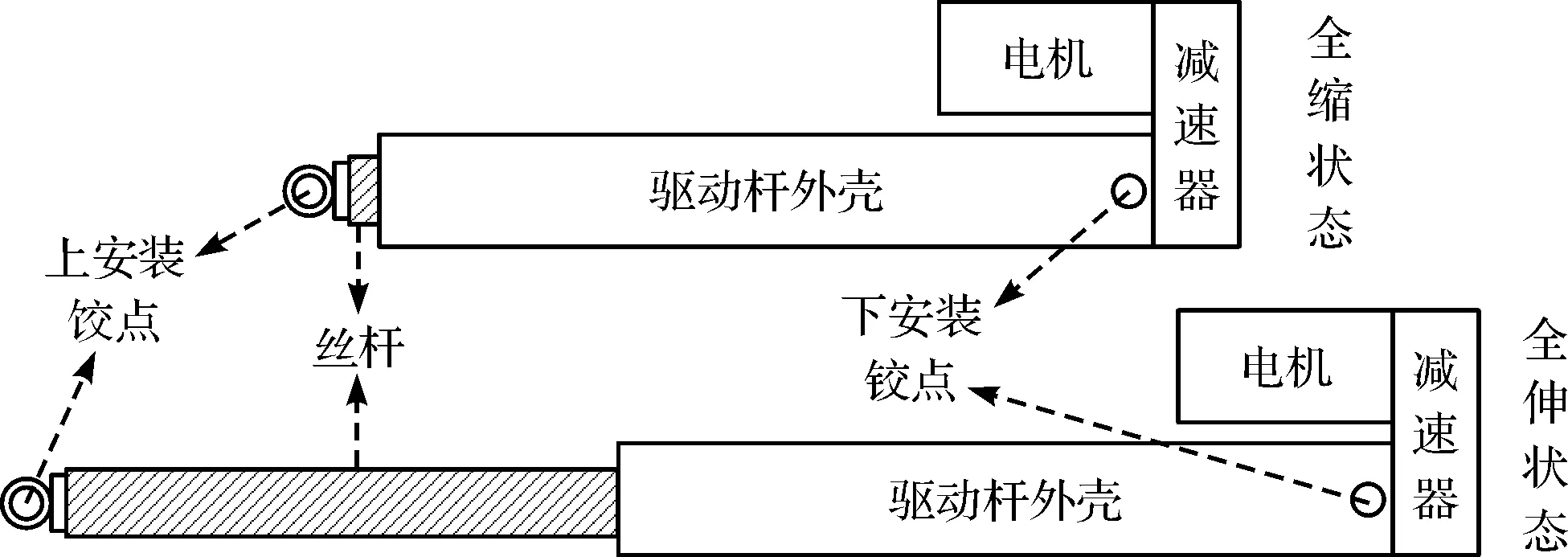
图2 电推杆总成结构

6 m SAWP剪叉机构的具体参数如表1所示。

表1 剪叉机构参数

1.1 运动学建模

在图1中,笔者根据空间位置分析法,构建了以A点为坐标原点,以AB和AI方向为轴和轴正方向的剪叉机构二维空间坐标系。

点S和点N的空间位置与举升角α之间的关系为:

(1)

式中:a—点S距离点O3的水平垂直长度;b—点S距离臂EH的垂直长度;c—点N距离臂AD的垂直长度;d—点N距离点O1的水平垂直长度;l—剪叉臂的长度;α—剪叉臂与轴正方向的水平夹角,α∈[αmin,αmax]。

同理,可以得到点O1～点O5的空间位置与的关系,即式(2):

(2)

所以平台底端距离铰点A的垂直高度H以及电推杆两个铰点间的长度lSN与α的关系为:

(3)

在α空间域内,平台升降速度vp与电推杆伸缩速度vl随时间t变化的运动学表达式为式(4):

(4)

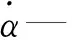
1.2 动力学模型

根据虚功原理[13]可知,升降过程中的驱动杆推力Fl的做功与剪叉机构的势能之间满足以下关系:

(5)

式中:pi—图1中第i层剪叉臂的中心质量,i=1,2,3,4;p5—平台的质量;pm—负载质量;g—重力加速度。

α与电推杆和x轴负方向的夹角关系可表示为:

(6)

式中:θ—电推杆与x轴负方向的夹角,θ∈[0°,90°)。

根据式(1,2),由α变化引起的点S、点N以及点O1～点O5的空间位置变化量,可进一步表示为:

(7)

(8)

故有:

(9)

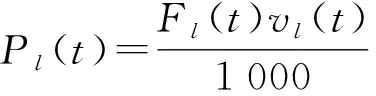
(10)

式中:Pl—电推杆输出端功率。

则电推杆电机输出功率Pm可表示为:

(11)

式中:il—电推杆总成能量传输效率;Tm—电机输出扭矩;nm—电机输出转速。

基于上述机理分析,笔者利用AMESim软件构建了举升机构仿真模型,如图3所示。

图3 举升机构仿真模型

当平台举升速度、升降高度、平台负载、电推杆长度等参数确定后,可利用式(4,9-11)确定电推杆的总成动力参数。

1.3 优化问题模型

由式(9)可知,在剪叉臂结构确定的情况下,α由αmin增加到αmax的过程中,驱动杆最大推力Fl_max的大小取决于4个值,即a、b、c、d。也就是说,在保证平台举升性能不变的情况下,选择合理的点S、点N可实现Fl_max的最优化选择,从而达到优化电推杆动力参数的目的。

为此,可构建电推杆推力静态优化问题模型:

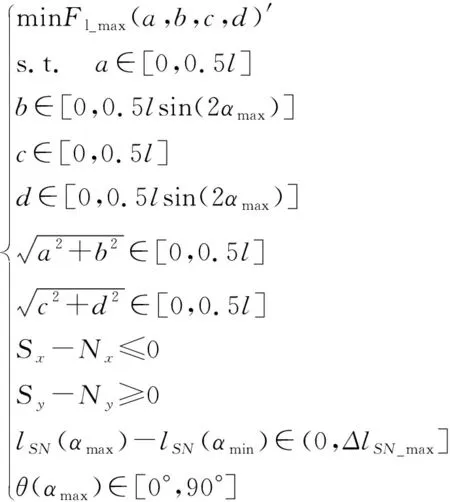
(12)

式中:ΔlSN_max—电推杆的最大伸缩量。

式(12)中给出的剪叉机构铰点优化问题属于单目标、多变量、非线性静态优化问题。

笔者将从全局优化、人工智能寻优以及梯度下降寻优3个角度设计铰点优化方法,以此确定出最佳铰点信息。

2 铰点位置优化

2.1 基于全局优化的优化方法

全局优化是指从符合条件的可行解中找出最优的一组解,其中遍历法[14]是全局优化方法的典型方法之一。

针对式(12)所述的静态非线性离散优化问题,笔者采用遍历法进行最优解的求取,其实现过程如图4所示。

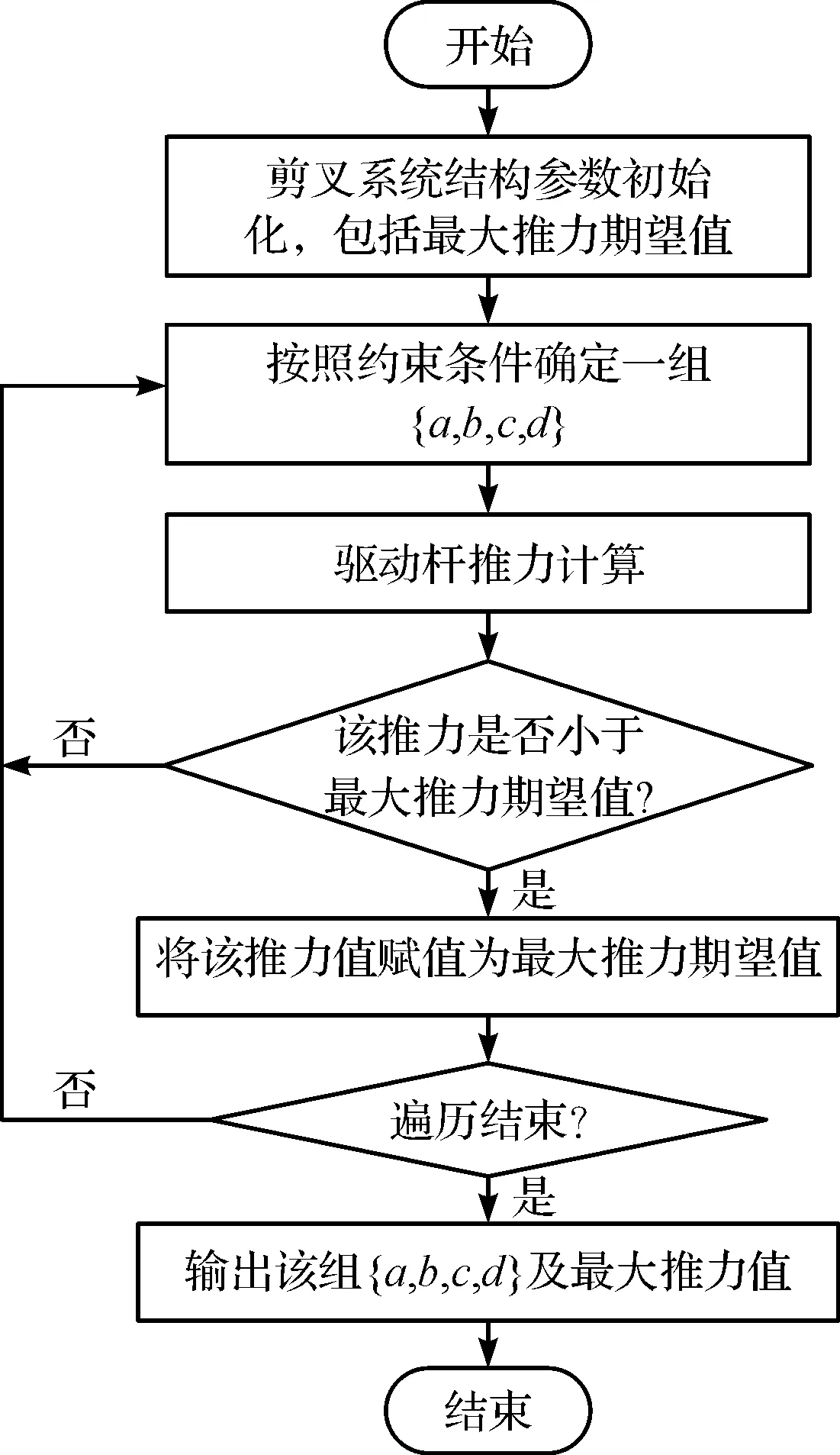
图4 基于遍历法的铰点优化流程图

2.2 基于人工智能寻优的优化方法

人工智能寻优是根据自然规律或生物行为设计的寻优方法,基典型特征是求解过程不需要遵循严格的解析机理,可以很好地应对复杂问题的求解。其中,粒子群算法[15]是一种典型的人工智能算法,可有效解决带约束条件的、离散非线性最优问题。相较于现有工作提出的遗传算法[16],该算法收敛速度快,降低了算法落入局部极小值点的概率。

根据粒子群算法的求解机制,可将问题模型式(12)中的变量定义为由m个个体组成的种群X:

(13)

其中,种群X中的每一个个体的信息都是潜在的可行解。

由此,可根据式(12)得出算法的适应度函数:

Fit=Fl_max(Xi),i=1,2,…,m

(14)

Fit(Xi)的值越小,表明对应的个体i的信息Xi越优。为此,个体i根据自身空间位置信息、移动速度以及种群中适应度值最优的个体的空间位置信息,按以下规则更新自身移动速度和位置信息:

(15)

根据粒子群算法可得到问题式(12)的求解过程,如图5所示。

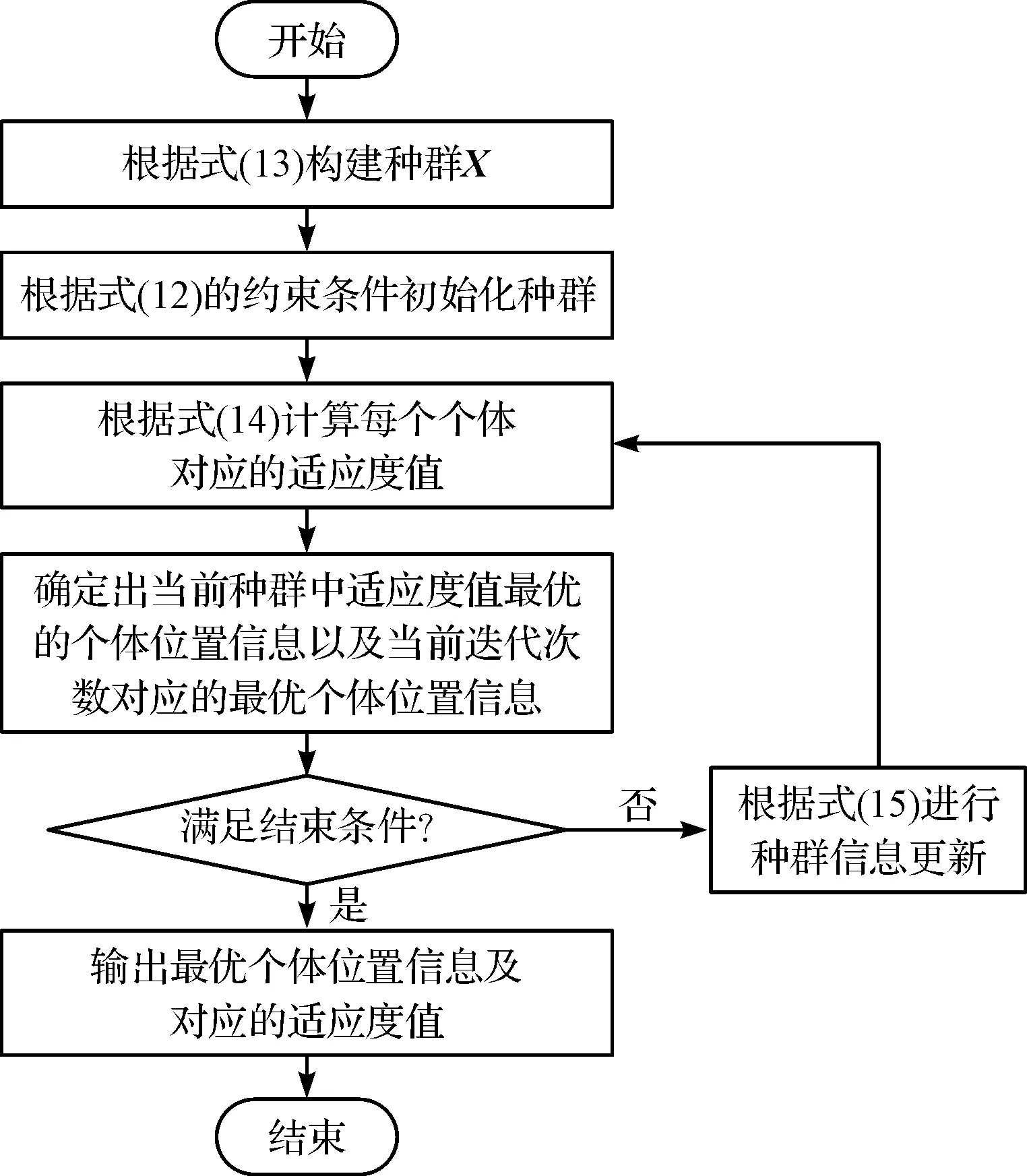
图5 基于粒子群算法的铰点优化流程图

2.3 基于梯度下降寻优的优化方法

梯度下降方法是典型的、通过解析手段求解非线性函数极值问题的方法径之一。其中,fmincon函数是MATLAB函数工具箱中提供的一种常用的利用梯度下降原理求解极值的方法[17，18],尤其适用于具体多约束条件的优化问题求解。

根据fmincon函数的语法规则,有:

(16)

由此可得式(12)的对应元素内容,即:

(17)

(18)

式中:xopt—最优解;fopt—最小推力;fun—求解函数;x0—变量初始值;[Al;bl;Aeq;beq]—线性约束;ub、lb—变量的上、下边界;nonlcon—非线性向量函数约束;options—默认优化参数。

根据上述语法定义好对应的元素内容后,即可在MATLAB中完成其最优解的求取。

3 性能对比实验

为了验证电推杆参数匹配的有效性,笔者以上述举升机构模型为平台,利用以上3种优化方法来确定电推杆的最优铰点位置;随后采用剪叉式高空作业平台的举升性能指标,对电推杆动力参数进行具体匹配;最后将以上操作获得的结果与液压驱动结果进行对比分析。

3.1 铰点位置优化实验

为有效分析所述3种优化方法在铰点优化效果方面的差异,实验将在相同的计算平台上完成。计算条件如下:处理器Intel(R) Core(TM) i5-4210U CPU @2.39 GHz,内存12 GB,操作系统Windows 10 64bits。

所述优化算法的初始条件设置如下:

(19)

采用3种优化方法得出了铰点位置信息以及对应的优化结果,如表2所示。

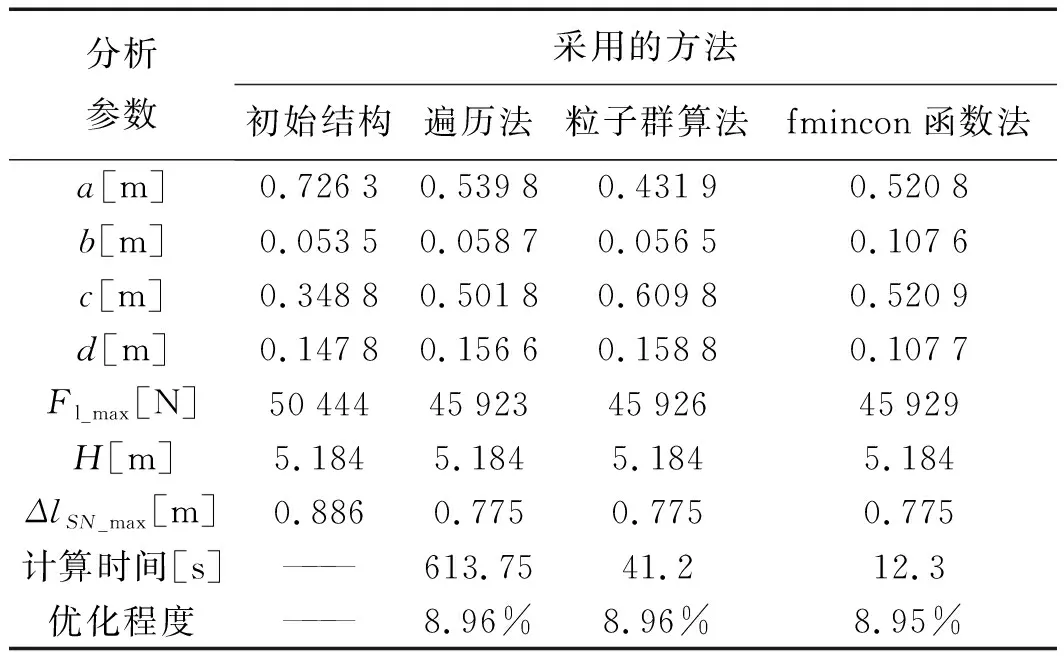
表2 铰点优化结果

在不同的铰点位置下,电推杆的推力变化曲线如图6所示。

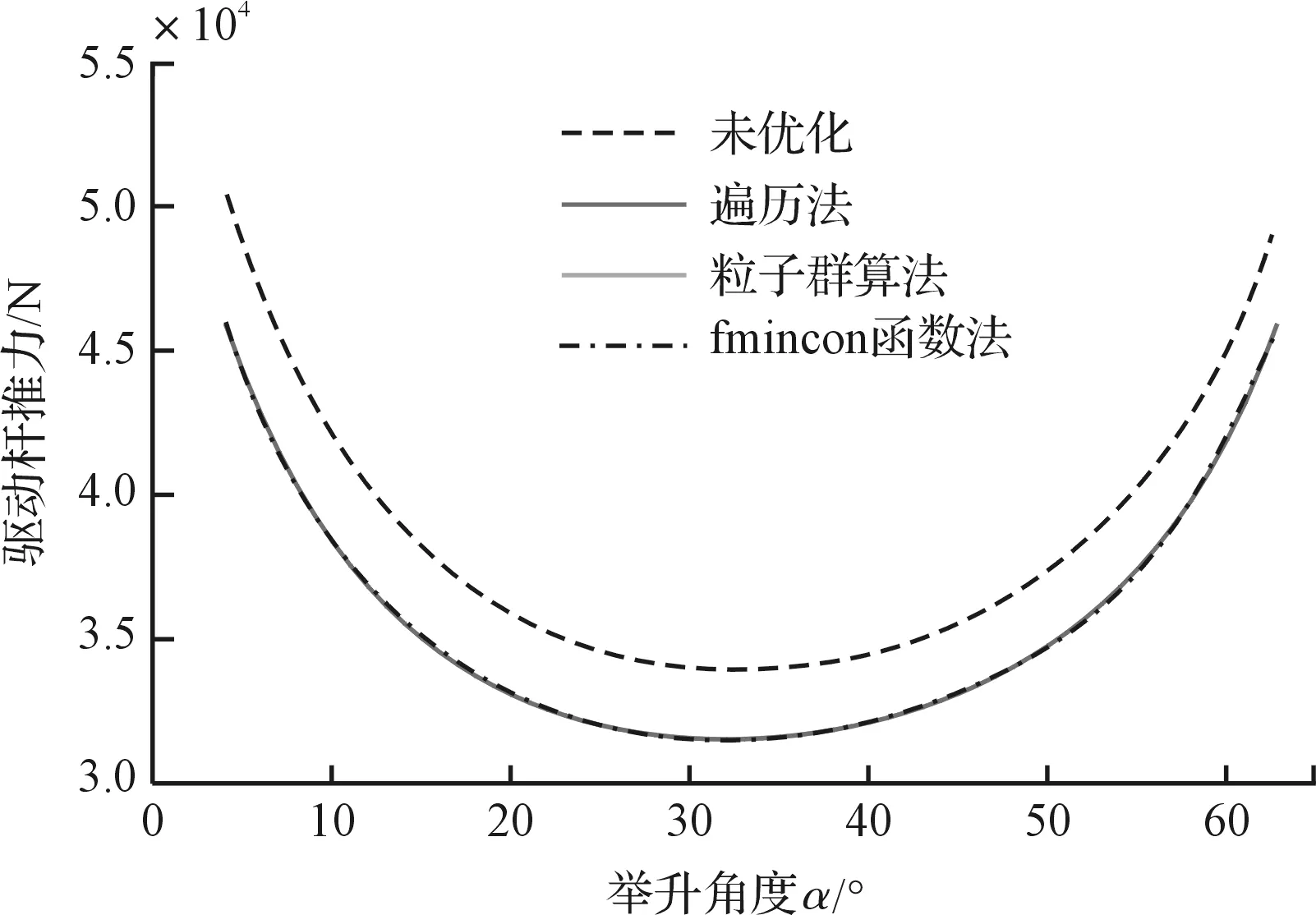
图6 不同铰点位置下电推杆推力变化曲线

图6给出了举升角度α由αmin增加到αmax的过程中,利用3种优化方法得出的铰点,仿真出的电推杆推力变化曲线。

结合表2和图6分析可知:(1)虽然3种优化方法在同一计算平台上完成优化需要的时间不尽相同,但是优化出的最大推力值近乎一致,且3种优化方法得出的推力变化曲线高度重合;(2)相较于未进行铰点优化的电推杆来说,经过铰点优化后的电推杆在保证平台举升高度不变,在满足电推杆伸缩长度限制的情况下,还可以有效降低电推杆的最大推力,进一步缩短电推杆的伸缩长度;(3)3种优化方法优化后的电推杆对应的最大推力均降低了约8.96%,伸缩长度均降低了0.111 m。

由此可见,3种优化方法均可通过铰点优化来降低电推杆的最大推力和伸缩长度。同时,考虑到3种优化算法的优化效果近乎相当,故在对举升系统进行实际参数匹配时,可以根据实际计算条件选择合适的优化算法。

下面以表2中的遍历法所得到的优化结果为基础,按表1所选研究对象的举升性能指标进行电推杆参数的具体匹配。

3.2 动力参数匹配及实验验证

笔者根据表2确定的铰点位置以及表1所述的设计参数要求,分别利用式(3,4,9,10)计算电推杆所需要的动力参数。

最后匹配出的电推杆动力参数如表3所示。

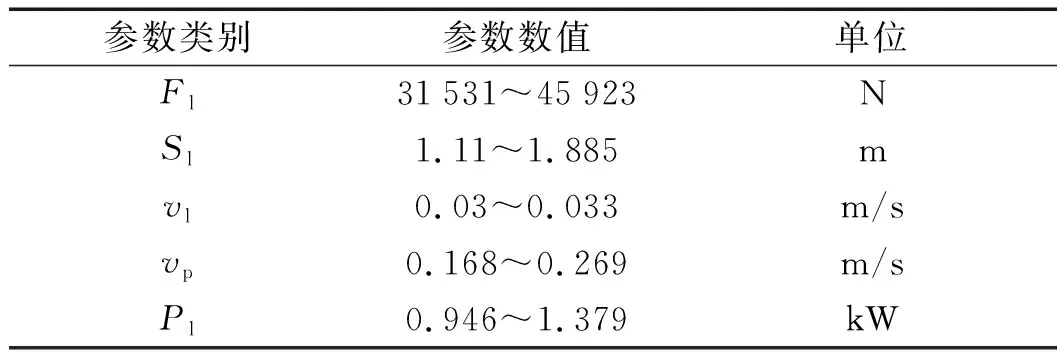
表3 电推杆动力参数

根据表3参数,笔者选择某型电推杆作为举升机构仿真模型的驱动杆,同时将其与剪叉式高空作业平台的原始液压系统进行对比实验。

实验选择的电池组参数为24 V—80 Ah,电池荷电状态(state of charge,SoC)在常温下的使用范围为30%～80%。

实验后得到了两种驱动方式对应的驱动性能对比结果,如图7所示。

图7 两种驱动方式对应的驱动性能对比

其中:举升角度随举升时间变化的曲线如图7(a)所示,随举升时间变化的推力曲线如图7(b)所示,随举升时间变化的平台升降速度曲线如图7(c)所示,两种驱动系统完成一个升降动作对应的电池SoC随时间变化的曲线如图7(d)所示。

由图7(a)可知:两种驱动方式在举升角度α由αmin增加到αmax的过程中,所用时间近乎一致,举升和下降时间分别约为24.5 s和26 s,满足表1所示升降时间的设计要求;

由图7(b)可知:在完成相同举升动作的前提下,电推杆的推力变化范围为31 733.4 N～48 699.1 N,液压油缸的推力范围为34 356.4 N～53 721.7 N,前者的最大推力比后者小5 022.6 N,平顺性也要比后者更突出,尤其在举升、下降动作起始阶段,后者的推力波动明显;

由图7(c)可知:液压油缸在举升及下降起初的2 s内,平台速度波动范围明显大于电推杆的速度变化范围;此外,当两种驱动方式速度稳定后,液压油缸对应的平台速度范围为0.16 m/s～0.278 m/s,电推杆对应的平台速度范围为0.17 m/s～0.274 m/s,满足表1所述的升降速度≤0.4 m/s的要求;

由图7(d)可知:由于电推杆的机械传输效率要比液压油缸的高,在举升阶段时,电推杆的电能消耗量比油缸小;且在平台下降过程中,电推杆同样可以依托电机,将平台的部分势能以能量回收的方式存储在电池组中,使电池组处于充电状态,液压油缸则不具备该功能。

具体来说,一个升降循环后,电推杆和液压油缸对应的SoC下降值分别为0.06%和0.323%,这说明电推杆的电能利用率要比液压油缸提高约81.3%。

由以上分析可得:在保证平台推力和升降速度与液压油缸相当的情况下,电推杆比液压油缸的电能利用率提高约81.3%,说明举升系统的电动化不仅可以克服液压油泄漏的问题,还可以通过势能回收提高电能的利用率,从而降低电池组的总装机容量,为降低整机制造成本提供可能。