近海废弃物打捞装置流场分析与优化研究*

王 春,闫纪媛,杨福芹,何 燕

(青岛科技大学 机电工程学院,山东 青岛 266061)

0 引 言

目前,海洋污染问题的严重性已经引起了全球各个国家的广泛重视,各国均对海洋废弃物打捞装置进行了研究。

BIAN Huai-qiang等人[1]设计了一种水面废弃物清理船,并对动力推进装置的推进轨迹进行了分析研究。CHEN Shi-yong等人[2]设计了一种多用途垃圾清理船,对水面漂浮垃圾的环保高效收集功能进行了研究。ZHANG Wei等人[3]为小型垃圾清理船设计了一种以锂电池为主要能源、太阳能为辅助能源的推进系统,对小型清洁船的动力系统进行了研究,提高了其环保性能。袁斌华等人[4]提出了一种搭载智能控制系统的小型水面清理船,对清理船的主控制电路进行了设计,提高了清理船工作过程中的自动化程度及其安全性。朱永强等人[5]设计了具有垃圾聚拢及垃圾导流装置的海洋垃圾回收船,对垃圾收拢、导流、传输、分流的回收过程进行了分析,提高了单人回收水面垃圾的效率。吴海都等人[6]研制了一种遥控式水面垃圾清理装置,对打捞工作以及水面监测工作进行了远程控制设计,实现了该装置在清理水面垃圾方面的智能化。卢思雨等人[7]设计了一种水车式湖面垃圾清理及水体增氧双体船,并增加了水体中的含氧量装置,提高了清理作业过程中水生动物存活率。陈玲等人[8]设计了水面垃圾清理船的回收与分拣系统,对水面垃圾自动收集和垃圾分类功能进行了研究,提高了垃圾的回收率[9]和可循环利用率。BAI Yue-jie等人[10]研制了一种小型节能水面垃圾清理机器人,对一次性部署水面垃圾收集范围进行了设计,从而提高了其收集效率。

但是上述研究均侧重于对水面垃圾清理船某种功能的设计与实现,没有进行相应的性能分析。

笔者对近海废弃物打捞装置中吸取单元进行流场分析,研究不同航速以及吸取口水下深度对吸取速度和吸取压力的影响,并运用Kriging近似模型,采用NSGA-II算法对吸取口吸取速度和吸取压力进行多目标优化,获取最优目标值,以提高打捞装置的吸取效率。

1 理论模型

1.1 几何模型

笔者采用SolidWorks软件建立近海废弃物打捞装置三维示意图,如图1所示。

图1中,吸取口、液压伸缩装置和不锈钢折叠软管组成吸取单元。

“棱锥形”吸取口尺寸如图2所示。

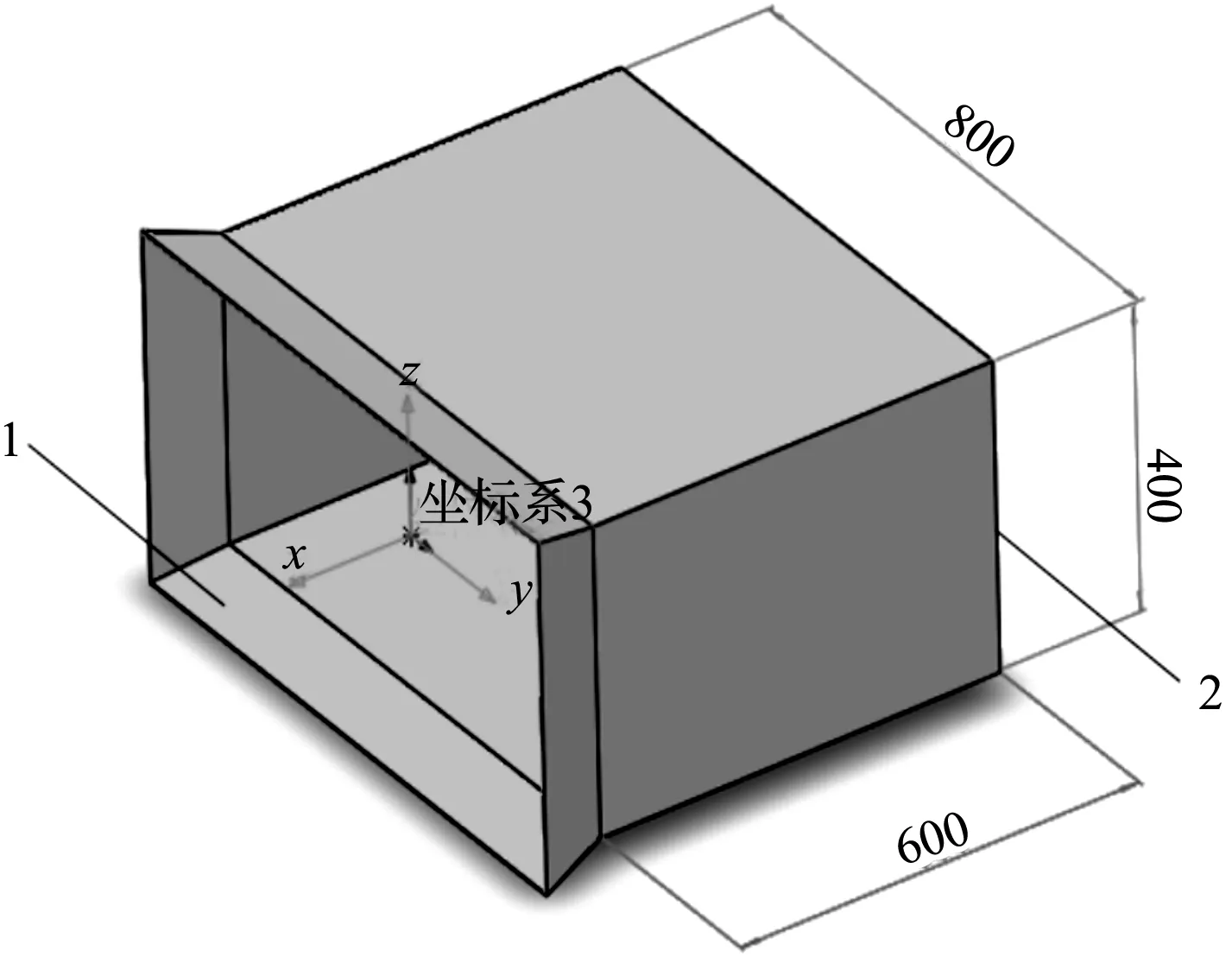
图2 “棱锥形”吸取口1—入口;2—出口

1.2 控制方程

质量守恒方程为:

(1)

式中:xi—坐标系中的i方向分量;ui—流体质点在i方向的平均速度分量,i=1,2,3;ρ—空气密度,kg·m-3。

动量守恒方程为:

(2)

式中:p—静压,Pa;τij—应力张量。

能量守恒方程为:

(3)

式中:μi—流动速度时均值,m·s-1;-ρμiμj—雷诺应力,N。

吸取单元的吸取口主要受到水下水流冲击作用,因此,笔者采用Standardk-ε湍流模型进行其内部流体分析[11,12]。

湍动能k方程为:

(4)

式中:Gk—平均速度时梯度湍流动能;Gb—由浮力引起的湍动能k的生成项,对不可压缩流体,Gb=0;μ,μt—层流和湍流黏性系数,kg·(m·s)-1。

Gb的表达式为:

(5)

湍动耗散率ε方程为:

(6)

式中:C1ε,C3ε—紊流系数。

Gk的表达式为:

(7)

(8)

式中:gi—重力加速度在i方向分量,m/s2;Prt—湍动Prandtl数,Prt=0.85;T—温度,K。

热膨胀系数β的表达式为:

(9)

2 参数设置

2.1 吸取口外包流域

笔者将图2所示的吸取口三维模型导入Workbench中的Flow Fluent模块,利用Ecloser操作方法建立其外包流域,吸取口模型位于流域的右上方。

吸取口在水下深度为50 mm的流域划分如图3所示。

图3 吸取口流域的划分1—流域入口;2—流域出口

2.2 网格划分

为了使模拟结果更为精确,笔者将整个模拟区域皆定义为流体区域(Fluid),并将三维模型导入Meshing模块进行网格划分;整个流域以及吸取口三维模型,采用非结构化网格划分,部分网格划分采用局部加密;在流域中设置边界条件,分别是进水口(Inlet)和出水口(Outlet),其余边界均作为壁面(Wall)。计算区域的网格数量都在1.20×106左右。

流域网格模型如图4所示。

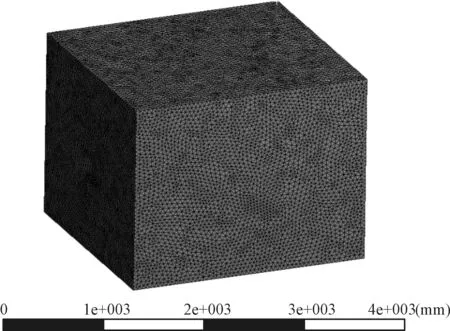
图4 流域网格模型

2.3 Fluent设置

为简化计算,此处只考虑航速和水下深度对吸取单元内部流场影响。笔者将流域入口设置为速度入口,给定初始速度值为10 m/s;流域出口设置为压力出口,其值与外部环境压强相等;其余壁面设置为标准壁面。

计算过程选择非耦合解法、隐式算法、瞬态过程;动量方程和连续性方程的残差收敛精度设为1×10-3,压强设为常压,激活重力选项,重力加速度为9.81 m/s2;计算过程采用时间迭代,迭代步数为0.002 s,每50步保存一次。

2.4 网格无关性检验

笔者以时间步长0.002 s,对5种网格数量进行无关性检验,通过仿真模拟其达到稳态后,得出结果,如表1所示。

表1 网格无关性检验结果

由表1可以看出:当网格数量超过约1.20×106时,仿真结果已经收敛,且对吸取压力和吸取速度模拟结果十分接近,具有较小影响,即网格数量增大到一定程度后计算结果趋于稳定。

综合考虑计算时间与仿真误差,笔者认为网格数量为1.20×106时可满足网格数量的无关性要求。

2.5 时间步长无关性检验

笔者按模型网格数量为1.20×106,对时间步长0.01 s、0.005 s、0.002 s、0.001 s,进行时间独立性检验。在模拟其进入稳定状态后,得出的计算结果如表2所示。

表2 时间步长无关性验证

由表2可得:在网格数量达到一定程度后,时间步长对吸取压力、吸取速度的模拟结果趋于稳定,差异不大。因此,为满足时间步长的无关性要求,笔者选取时间步长为0.002 s。

3 仿真及结果分析

为更加直观表达吸取口内外流域的速度、压力变化趋势,笔者沿图2中XY截面精选不同的速度与压力点,将数据文件导入Origin软件中进行后处理,得到吸取口XY截面速度变化曲线与压力变化曲线。

3.1 不同航速下的速度和压力分布

笔者分别设置航速为1 m/s、5 m/s、7 m/s、10 m/s,吸取口在水下深度为100 mm,运行时间为2 s,以吸取口中心为原点,得到吸取口XY截面速度云图和速度曲线图,如图5所示。

图5 距水面100 mm吸取口XY截面速度云图与曲线图

由图5可以看出:(1)航速越小,速度梯度变化越不明显,航速v=1 m/s时,“棱锥形”吸取口周围的流速无明显变化,吸取速度最低;

(2)在各种航速下,水流冲击外扩板出现反弹现象,导致吸取口周围的速度降低,形成一个近乎圆形的速度区间,且随着航速的增大,圆形速度区间逐渐增大;而在外扩板内侧吸取速度较大,压强小,外扩板外侧速度区间出现“蓝区”,流体流动速度慢、压强大,使得吸取口外侧废弃物由压强大的区域向压强小的进口处移动,进而加快海洋废弃物的收集;

(3)由于流体冲击外扩板引起的反弹现象,沿XY截面4种航速下的吸取口速度均呈现先降低后增加的趋势;随着航速的增大,吸取口周围的速度逐渐增大,吸取单元吸取废弃物速度也逐渐增大,其中,航速为10 m/s时,吸取速度最大。

同等工况条件下,得到吸取口XY截面压力云图和压力曲线图,如图6所示。

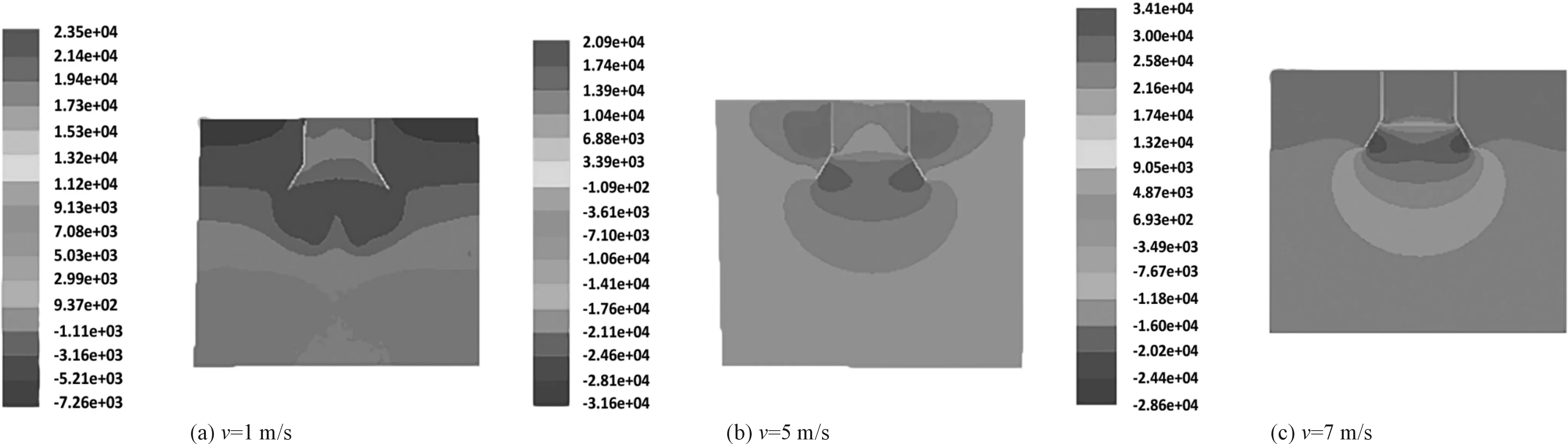
图6 距水面100 mm吸取口XY截面压力云图与曲线图在打捞装置工作过程中,吸取单元在水中的压力方向与水流流动的方向一致

由图6可以看出:从边界入口至边界出口,压力逐步递减;在水流接触到吸取单元之后,吸取口前端形成了较大的压力区,而吸取口内部压力要小一些,所以在打捞装置以一定速度前行的过程中,海洋废弃物会在水压和水流速度的作用下,向吸取口流动,完成对废弃物的吸取过程;

对比不同航速下吸取口XY截面压力变化曲线可以看出:在航速为10 m/s时,吸取口高压区间较长,水流流动速度较快,吸取单元吸取废弃物速度较快,吸取效率较高。

3.2 不同深度下的速度与压力分布

假设废弃物在水下的最大深度为200 mm,为研究不同水下深度吸取口流场的流体状态,笔者设置航速10 m/s,吸取口水下深度分别为50 mm、100 mm、150 mm、200 mm,对应得到吸取口流场速度云图和速度曲线图,如图7所示。

图7 航速为10 m/s吸取口XY截面速度云图与速度曲线图

由图7可以看出:(1)由于外扩板的原因,流体冲击外扩板反弹,导致沿着流域进口边界至出口边界,吸取口吸取速度先降低后升高;(2)在相同的航速下,4种深度的吸取口流域速度分层较明显,且随着深度的增加,速度梯度变大,吸取口吸取速度变大;(3)吸取口外侧速度分布出现“蓝区”,此处流场速度小、压强大,在一定程度上提高了吸取效率;(4)吸取口水下深度h=150 mm与h=200 mm的速度曲线几乎重合,因此当h>150 mm时,深度对吸取速度几乎不产生影响。

同等工况条件下,得到吸取口XY截面压力云图和压力曲线图,如图8所示。

图8 航速为10 m/s吸取口XY截面压力云与压力曲线图

由图8可以看出:(1)随着吸取口水下深度的增加,吸取口前端的压力梯度变大,吸取口两侧的高压范围增大;(2)h=150 mm与h=200 mm的压力曲线几乎重合,因此当h>150 mm时,深度对吸取压力几乎不产生影响。

4 工况参数优化

4.1 试验设计

为提高吸取单元吸取效率,得到吸取速度与吸取压力的最优解,笔者利用最优拉丁超立方法进行仿真试验设计,使样本点均匀的分布在样本空间上,保证试验因子与响应值更加真实可靠地拟合[13]。

笔者将航速v和水下深度h作为设计变量,航速初始值为10 m/s,取值范围为[0.5,10],水下深度的初始值为73 mm,取值范围为[50,150];

笔者将吸取单元的吸取速度V0和吸取压力P作为评价指标,基于Isight软件中的DOE模块,按照设计变量数的20倍进行了抽样,抽取了40组样本点;运行Fluent软件,求取了40组样本点对应的吸取单元吸取速度和吸取压力;随即采用NSGA-II(Non-dominated Sorting Genetic Algorithm)算法,生成了最优解集,得到了最优航速与水下深度。

4.2 Kriging模型

克里金法(Kriging)是依据协方差函数对随机过程或随机场进行空间建模和预测(插值)的回归算法[14],克里金法在工程问题的数值试验中可作为代理模型(SM)对有限的模拟结果进行插值[15]。

笔者利用40组样本点,在Isight软件中的Approximate功能模块建立了Kriging近似模型。因各设计变量间的数量级不同,笔者选择Anisotropic拟合类型;将平均绝对误差(average absolute error,AMAE)、最大绝对误差(maximum absolute error,MAE)、均方根误差(root mean squared, RMS)和判定系数(R-square,R2)作为模型精度评价指标,选择Cross-validation进行了误差分析,得到误差分析结果,如表3所示。

表3 Kriging模型误差分析

分析表3后的结果表明:AMAE和RMS都小于0.1,MAE小于0.3,R2大于0.9,即可认为近似模型具有较好的拟合效果。由此可见,吸取单元吸取速度V0和吸取压力P均满足精度要求。

4.3 吸取单元工况参数优化

笔者采用NSGA-II算法(一种非支配排序遗传算法),通过对解域进行分析,生成Pareto最优解集(它能保持多样性和更好的精英策略,即保证优良群体不断进化,直到进化的解决方案不如前一解决方案为止[16,17]);然后,笔者利用NSGA-II算法驱动Kriging模型,建立联合仿真工作流。

NSGA-II算法的详细参数设置如表4所示。

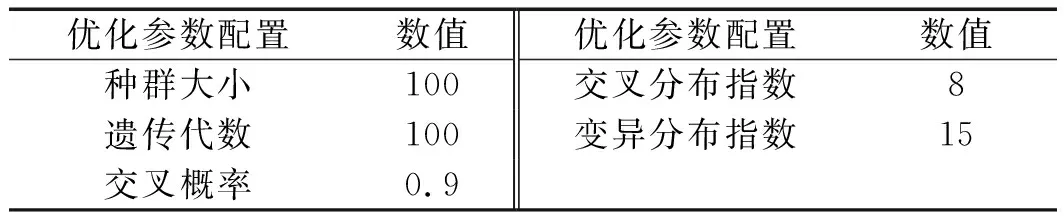
表4 NSGA-II参数设置

Isight平台通过选取可行解,删除劣质解,完成监控迭代过程,得到了最优设计变量组合,如表5所示。

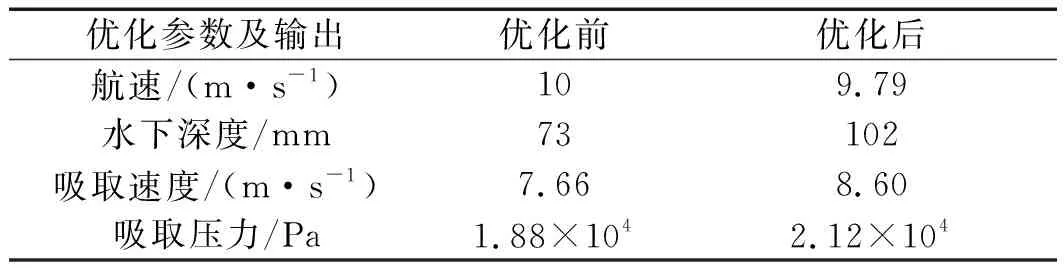
表5 优化结果

由表5可知:(1)优化后得到最优工况参数航速为9.79 m/s,吸取口的水下深度为102 mm,此时得到吸取单元的吸取速度由7.66 m/s增加至8.60 m/s,提高了12.3%;(2)吸取压力由1.88×104Pa增加至2.12×104Pa,提高了13.2%。

由此可知,经NSGA-II算法优化后，其吸取效率得到明显提升。

4.4 模型验证

笔者将最优工况参数(航速为9.79 m/s,水下深度为102 mm)导入Fluent中吸取口分析模型,得到吸取单元吸取速度云图和吸取压力云图,如图9所示。

图9 吸取口v=9.79 m/s,h=102 mm时XY截面云图吸取速度为8.08 m/s,吸取压力为1.98×104 Pa

最优工况参数下,吸取单元吸取速度和吸取压力的仿真值与优化值对比结果,如表6所示。

表6 仿真值与优化值对比(误差)

由表6可知:仿真值与优化值两者相对误差均在10%以内,表明该联合仿真模型(Kriging+NSGA-II)具有较好的预测精度,可以高效、准确地获取最优目标,避免了复杂、耗时的仿真过程。

5 结束语

笔者建立了近海废弃物打捞装置吸取单元吸取口模型,分析了不同航速下,水下深度吸取口的吸取速度、吸取压力数值变化;其次,基于Kriging近似模型,建立了吸取口工况参数与吸取效率之间的映射关系,并结合NSGA-II算法进行了吸取单元工况参数的多目标寻优。

研究结论如下:

(1)当吸取口水下深度一定时,随着航速的增大,吸取速度逐渐增大,吸取压力先增大后减小;当航速一定时,吸取速度随着深度的增加而增加,吸取压力先增大后趋于平稳;

(2)采用Kriging近似模型和NSGA-II算法对吸取口进行了多目标寻优,得到了吸取口最优工况参数(即航速v=9.79 m/s,水下深度h=102 mm);优化后吸取口的吸取速度提高了12.3%,吸取压力提高了13.2%,且优化值与模拟值之间的相对误差均在10%以内,表明联合仿真模型(Kriging+NSGA-II)是可靠的。

在后续研究中,笔者将探索打捞装置结构参数以及吸取口形状等因素对吸取效率的影响,从而最终达到进一步提高打捞装置吸取近海废弃物效率的目的。