基于梁截面的商用车驾驶室多目标优化研究*
2022-02-28汤金帅刘夫云邓聚才刘凯扬
汤金帅,刘夫云*,邓聚才,刘凯扬
(1.桂林电子科技大学 机电工程学院,广西 桂林 541004;2.东风柳州汽车有限公司,广西 柳州 544005)
0 引 言
汽车车身的各项性能指标不仅会影响用户乘车体验,还直接关系到其生命安全。每款汽车[1]在批量生产之前,都必须经过NVH(即:Noise-噪声、Vibration-振动、Harshness-声振粗糙度)、碰撞安全性、操纵稳定性、结构耐久性等测试,性能达到要求后才能进入下一阶段。
众所周知,车身刚度[2]极大地影响汽车各项性能。车身刚度不足,会造成汽车模态偏低,易发生共振。已有的研究表明,梁截面形状、板厚是影响车身刚度的两大主要因素。通过研究上述两种因素与车身刚度之间的主效应关系,能够帮助工程师设计出更符合市场需求的汽车。
郭润清等人[3]采用比例向量法,对乘用车的梁截面形状进行了控制,以轻量化为目标,利用粒子群优化算法对其进行了轻量化优化,优化后质量减轻了1.86%;但该研究的轻量化百分比较低,轻量化效果有待进一步提升。姚再起等人[4]建立了乘用车白车身的隐式参数化模型,通过参数化技术将白车身划分为梁与接头,结合有限元前处理软件,找出了对性能影响最大的结构、厚度变量,之后从截面、厚度、工艺3个不同角度进行了优化,优化结果表明,在质量基本不变的条件下,乘用车白车身的静态性能得到了一定提升;但该研究以刚度、模态为优化目标,没有进一步考虑车身的轻量化。秦欢[5]结合企业实际需求,通过尺寸优化、单截面优化、多截面优化、形状优化4个层级的优化,设计出了精确的迭代求精方法,为乘用车提供了实际有效的梁截面优化框架。
但乘用车与商用车的结构相差较大,结合企业实际需求,有必要面向商用车开展梁截面优化的相关研究。QIN H等人[6]采用比例向量法,对乘用车梁截面形状进行了控制,使用改进后的遗传算法进行了乘用车梁截面形状的优化,并通过12个测试函数对此进行了验证,结果表明,该方法能够极大地减少优化变量的数量,轻量化效果较佳;但该研究仅以轻量化为优化目标,考虑因素较少,还需进一步研究其多目标优化问题。
为解决上述问题,笔者提出一种基于梁截面的商用车驾驶室多目标优化方法;首先,建立驾驶室隐式参数化模型,并完成模型精度验证;其次,分析驾驶室梁截面力学特性,找出关键控制因素,利用比例向量法控制梁截面形状;再次,进行驾驶室厚度、梁截面灵敏度分析,筛选出关键优化变量,选用最优拉丁超立方法进行试验设计;最后,构建径向基—响应面混合近似模型,采用第二代遗传算法进行多目标优化。
1 隐式参数化模型建立
传统的梁截面优化方法大多是基于有限元模型进行的。但该方法有两个明显缺点:(1)优化变量上下限变化范围较小;(2)算法求解出的优化解,可能为局部较优解,而非全局最优解。
为了更好地解决上述问题,笔者采用隐式参数化模型来对商用车驾驶室的梁截面进行优化。
商用车驾驶室的有限元模型如图1所示。
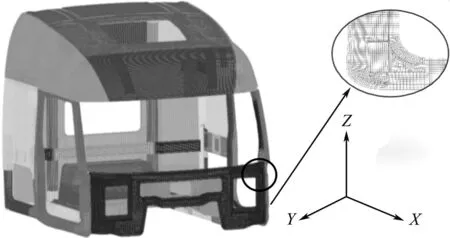
图1 商用车驾驶室有限元模型
驾驶室梁截面的优化流程框图如图2所示。
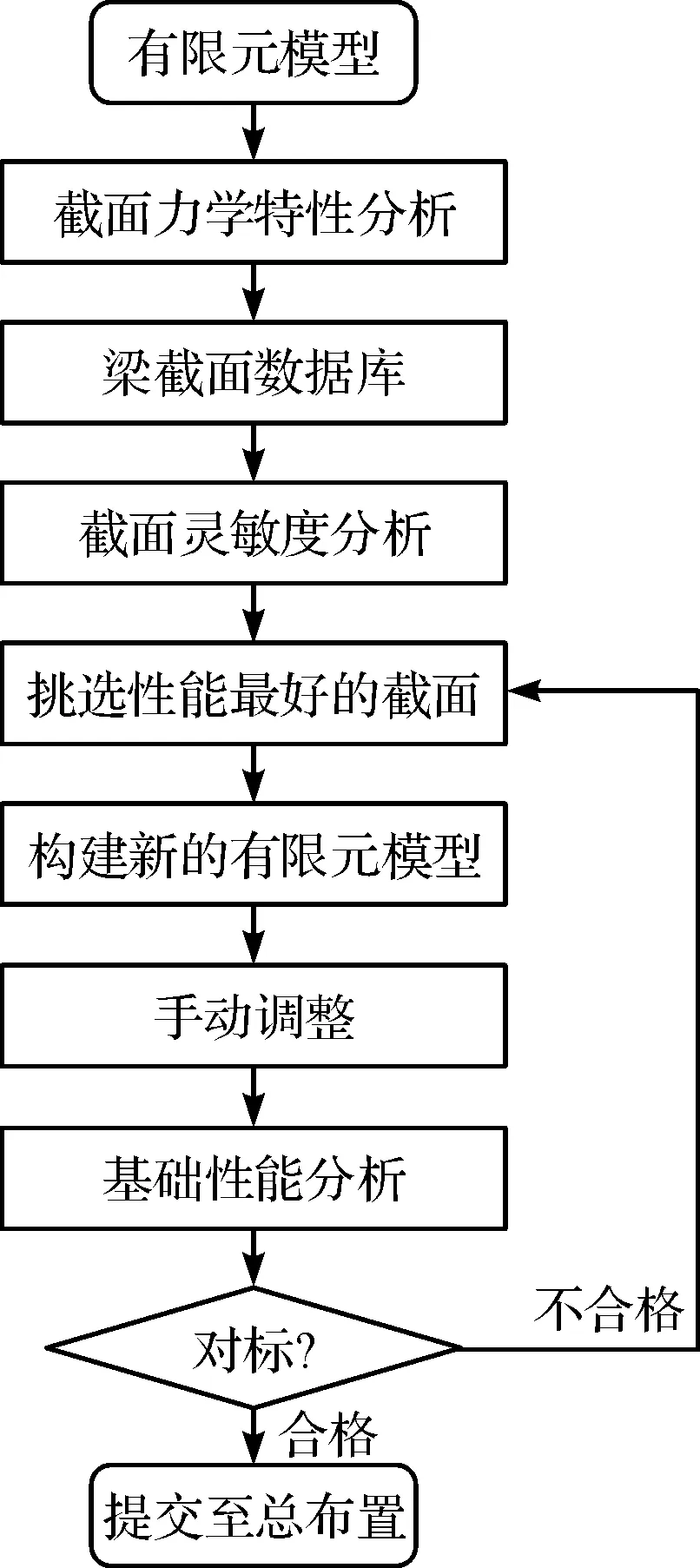
图2 梁截面优化流程框图
商用车驾驶室隐式参数化模型如图3所示。

图3 隐式参数化模型
该隐式参数化模型可以录制任意符合工程实际的变量;当零部件的位置、截面、厚度发生变化后,可以利用SFE-Concept一键生成满足拓扑关系的高质量网格。相较于有限元模型,采用隐式参数化模型进行结构优化,用户能得到性能更优的解,且其优化过程也更加智能化。
建立隐式参数化模型时,有时会忽略一些工艺需求上的小尺寸结构(如开口、小凸台等),但这时的模型精度势必会受到影响。因此,在进行工况分析前还需要验证模型的精度。
模型精度验证步骤如下:
(1)确定对比分析对象。隐式参数化模型是在有限元模型的基础上建立的(有限元模型已得到试验验证),故需要将有限元模型与隐式参数化模型进行对比分析;
(2)确定验证内容。汽车在行驶过程中,会受到来自各方面的激励,如发动机等;当汽车低阶振动频率接近激励源频率时,易发生共振与噪声,造成疲劳失效现象的产生,故需对自由状态下的低阶振动频率(一阶弯曲模态频率、一阶扭转模态频率)进行分析;同时,质量、扭转刚度、弯曲刚度为优化目标,需要计算优化百分比。由此确定驾驶室的质量、扭转刚度、弯曲刚度、一阶扭转模态频率、一阶弯曲模态频率为验证内容;
(3)利用optistruct求解器求得驾驶室的基础性能值。
驾驶室隐式参数化模型一阶振动模态的仿真结果,如表1所示。

表1 驾驶室隐式参数化模型一阶振动模态仿真结果
根据相关企业的标准,商用车驾驶室一阶振动频率需避开易产生共振的频率范围。相关企业给定的频率范围为24.6 Hz~28.6 Hz。
由表1可知:驾驶室一阶扭转模态频率为21.0 Hz,一阶弯曲模态频率为39.5 Hz,故驾驶室一阶振动频率符合相关企业标准。
驾驶室基础性能值如表2所示。
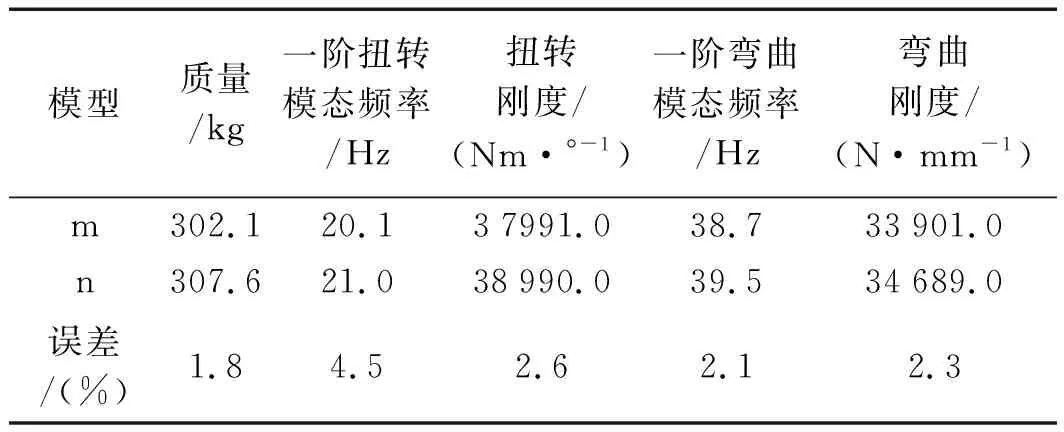
表2 驾驶室基础性能值
由表2可知:驾驶室各项基础性能值的误差均在4.5%以内,满足相关的精度要求。
2 截面及灵敏度分析
2.1 截面力学特性分析
梁截面的几何特性与力学特性对驾驶室的刚度起关键性的作用[7]。对驾驶室梁截面进行力学特性分析时,需要以垂直于梁的方向切割出梁截面,之后通过手动方式调整梁截面的几何形状,改变梁截面的力学特性,进而对车身进行优化,以提高其性能。
驾驶室梁截面截取示意图如图4所示。

图4 驾驶室梁截面截取示意图
梁截面的力学特性指标包括断面面积、截面惯性矩、封腔面积、扭转常数[8]。
梁截面的惯性矩原理图如图5所示。
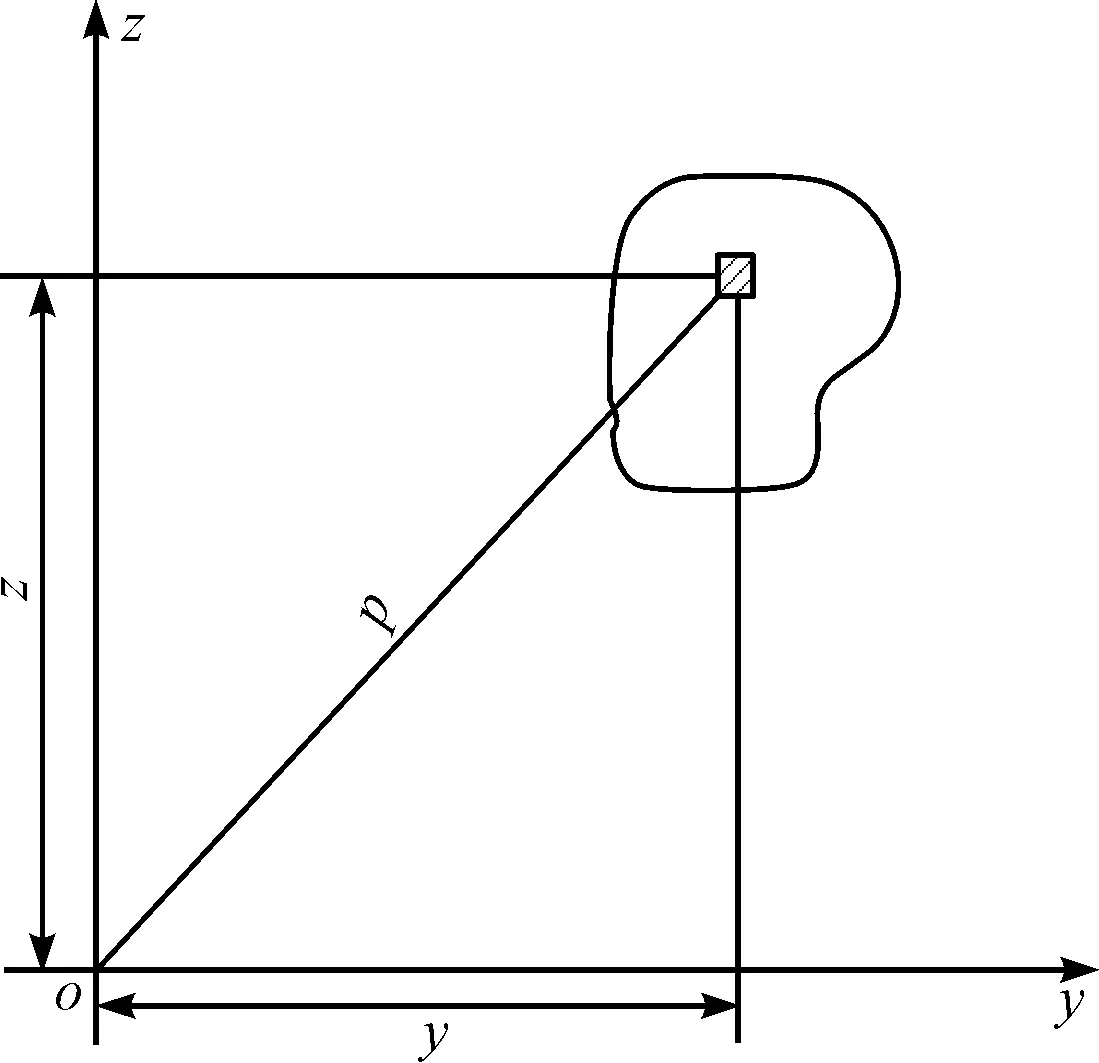
图5 梁截面惯性矩原理图
梁截面惯性矩计算公式如下:
(1)
(2)
式中:Iy—面积元素至z轴的惯性矩;Iz—面积元素至y轴的惯性矩;A—零件断面面积。
扭转常数计算公式如下:
(3)
式中:It—扭转常数;B—外形轮廓所围面积;t—薄壁杆厚度;S—截面中线周长。
部分梁截面力学特性分析结果如表3所示。
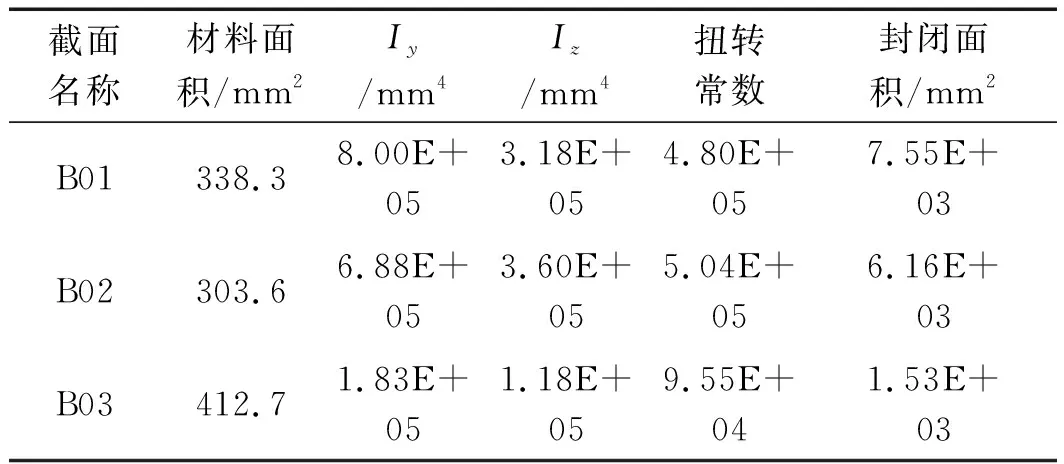
表3 梁截面力学特性分析结果
由于商用车驾驶室的结构复杂,所有零部件都通过焊接被连接在一起,当其中的一个钣金件发生变化时,都要对其关联结构进行调整。
为了满足工艺、装配的要求,在进行优化分析时,一般只对梁截面的内板以及加强板进行调整。此处以B01为例,用户利用SFE-Concept软件分别将梁截面内板位置向z向移动2 mm、梁截面内板厚度增加1 mm,可得调整后的梁截面力学特性值。
调整后的梁截面力学特性值如表4所示。

表4 调整后的梁截面力学特性值
表4中,z向参照图4的坐标系。
一般认为[9],截面形状、厚度为梁截面力学特性关键因素,由此,笔者选择截面形状与厚度作为优化变量。
2.2 梁截面形状控制方法
目前,控制梁截面形状的方法主要有4种:比例缩放法、极坐标法、矩形模拟法、比例向量法[10]。其中,比例向量法控制变量少,能够有效减少优化变量数量,且关于该方法的相关研究较多,理论上也较为成熟。
比例向量法的原理图如图6所示。
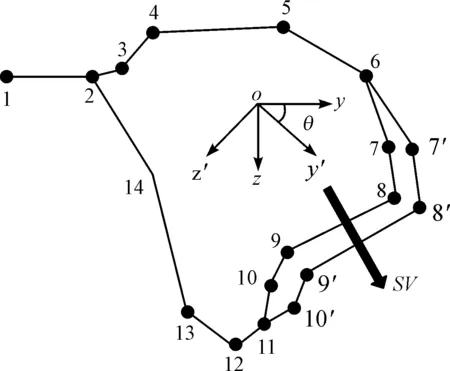
图6 比例向量法原理图
图6中,比例向量法通过改变旋转角度的大小来控制变化的方向,然后通过控制变形度量值SV的大小,实现梁截面的变化。
在yoz坐标系中,点7的坐标为(y,z),对该坐标系旋转一定的角度,在新的坐标系y′oz′中点7的新坐标为(y′,z′)。其计算公式如下:
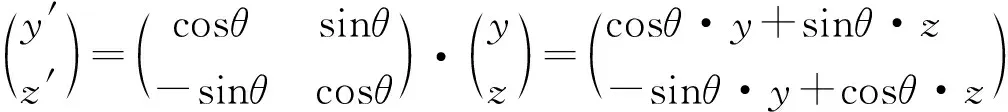
(4)
确定好旋转角度之后,再确定变形度量值SV的数值;发生变形后,可进一步得到点7移动后的坐标(y″,z″)。其计算公式如下:

(5)
将式(4)代入式(5)中,可得:
(6)
根据上述计算公式可知:当θ=0°时,基点坐标随y向变化;当θ=90°时,基点坐标随z向变化。
在进行梁截面优化时,工程实践中一般取θ=0°或θ=90°[11]。因此,笔者取θ=0°时,对上述商用车驾驶室梁截面进行优化研究。
除了以上4种主要的梁截面形状控制方法外,还可以通过控制基点坐标来控制梁截面的形状。
对于控制基点较少的单截面优化问题,可采用控制基点坐标控制截面形状,因为该方法原理相对较为简单,易于理解。而对于控制基点较多的多截面优化问题,采用比例向量法控制截面形状,可减少优化变量的数量。
2.3 灵敏度分析
工程实践中,一个优化问题往往有多个优化变量,如不加以筛选,会导致试验设计的运行时间过长。因此,需进行灵敏度分析,以筛选出对响应影响较大的变量,提升优化的效率。
灵敏度分析[12]是一种研究敏感程度的方法,其分析公式如下:
(7)
式中:s—灵敏度;∂f(x)/∂xi—目标函数f(x)对变量xi的倒数;i—第i个零件的厚度或截面形状。
目前,基于隐式参数化模型的梁截面优化方法,大多以试验设计的方式进行灵敏度分析[13]。该方法需要录制所有可能的优化变量,试验设计运行时间较长。
结合工程实际需求,笔者利用HyperMesh、HyperMorph分别进行厚度灵敏度分析、截面灵敏度分析,并在试验设计之前筛选出优化变量。该方法节省了计算资源,提升了优化效率。通过灵敏度分析可以计算出质量、一阶扭转模态频率、一阶弯曲模态频率、扭转刚度、弯曲刚度分别对于截面形状、板厚的灵敏度数值。
部分厚度灵敏度分析结果如图7所示。
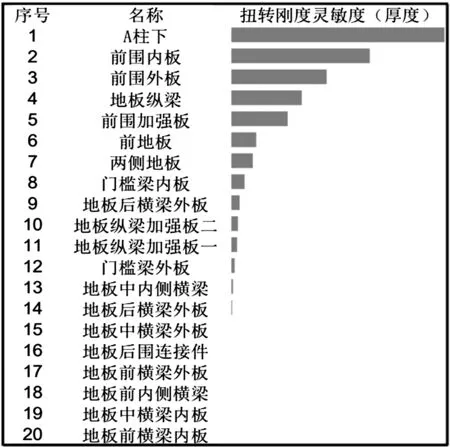
图7 厚度灵敏度分析结果
部分截面灵敏度分析结果如图8所示。
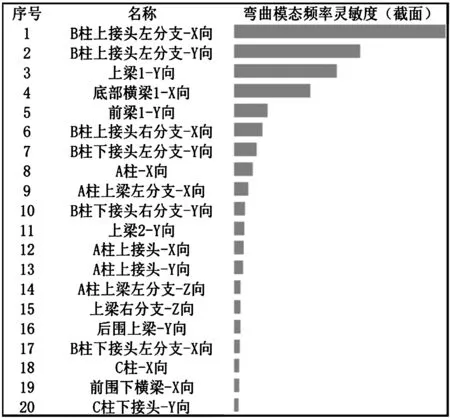
图8 截面灵敏度分析结果
柱状图的长短表示灵敏度数值的大小
由于灵敏度数值越大,表示变量对于目标的影响越大,笔者按照灵敏度数值大小降序排列,分别取每项前20个灵敏度数值最大的变量。经过筛选,笔者共选取33个厚度变量,45个截面变量作为此次优化的设计变量。
以该方式进行灵敏度分析,共需17.1 h,相较于以试验设计进行灵敏度分析的方式,运行时间缩短了40%,提升了优化效率。
3 近似模型
如果直接使用原始模型进行优化,将会大大降低优化的效率,故笔者采用近似模型来替代原始模型。所谓近似模型[14,15]即是通过采用一种数学模型的方式,来逼近输入与输出的函数关系。
近似模型拟合公式如下:
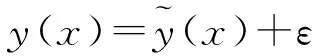
(8)
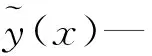
由近似模型拟合公式可知,近似模型与原始模型存在精度差,只有精度达到要求后,才能代替原始模型进行优化。一般通过相关系数R2及误差散点图进行评价。
R2计算公式如下:
(9)

当R2值越接近1时,表示近似模型拟合精度越高;当R2值不小于0.9时,可认为近似模型的拟合精度满足精度要求。
响应面法可以用较少的样本点,最大限度地逼近目标函数;同时该方法拟合形成的近似模型简单,具有较强的鲁棒性。因此,工程实践中常采用响应面法来拟合近似模型。
但对于具有高度复杂函数关系的优化问题而言,该方法拟合效果较差,性能指标的相关系数值往往不能同时满足精度要求。拟合结果表明,采用响应面近似模型的质量、扭转刚度、一阶扭转模态频率、弯曲刚度、一阶弯曲模态频率相关系数值分别为0.999、0.995、0.978、0.938、0.851,一阶弯曲模态频率相关系数值为0.851,未达到精度的要求。
对于高度复杂的函数关系,径向基法逼近效果较佳。因此,笔者构建径向基—响应面混合近似模型,以提升一阶弯曲模态频率的拟合精度。
混合近似模型的拟合精度如表5所示。

表5 混合近似模型拟合精度
由表5可知:混合近似模型的一阶弯曲频率相关系数值为0.901,到达了精度要求。
质量拟合精度误差散点图如图9所示。
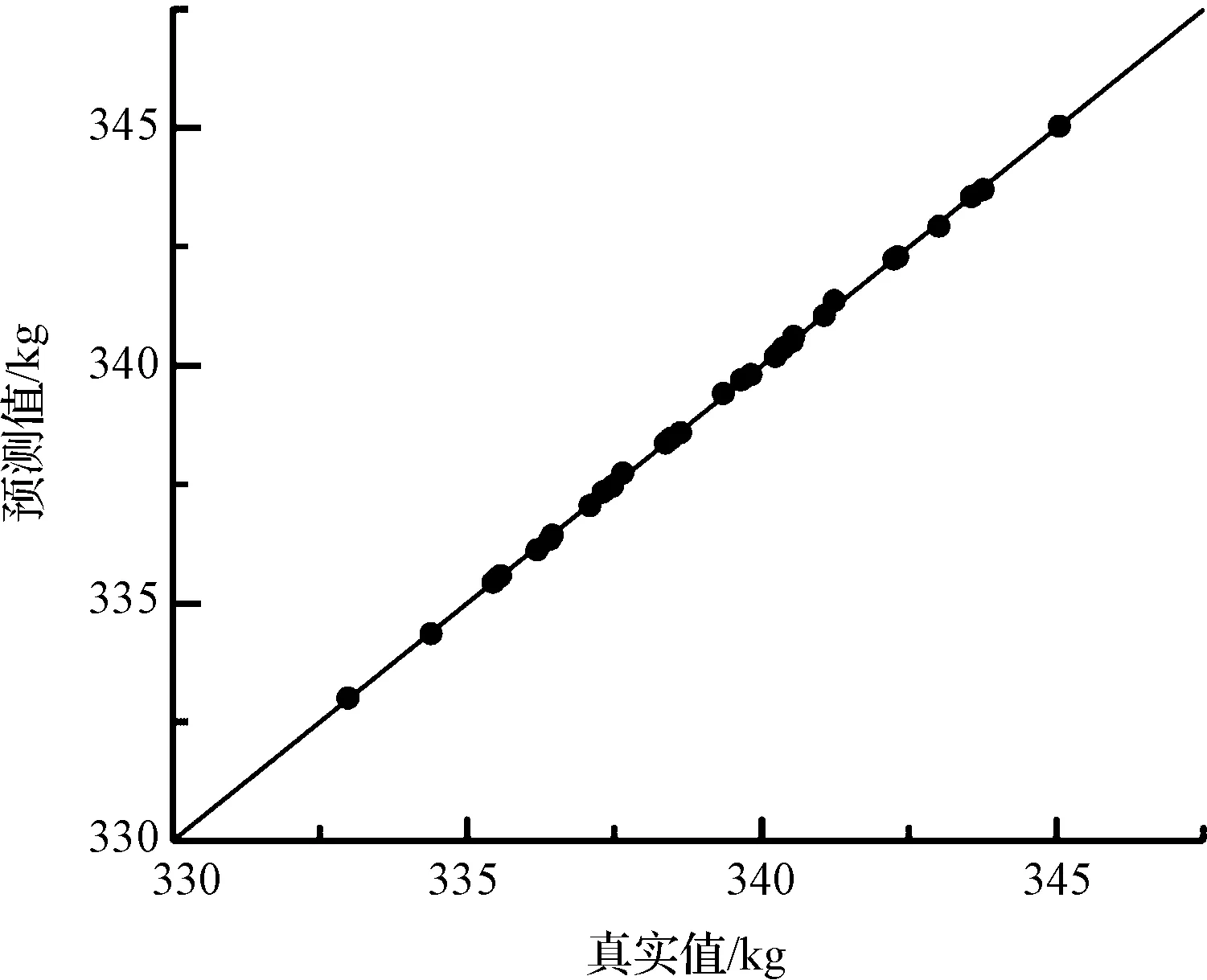
图9 质量拟合精度误差散点图
扭转刚度拟合精度误差散点图如图10所示。
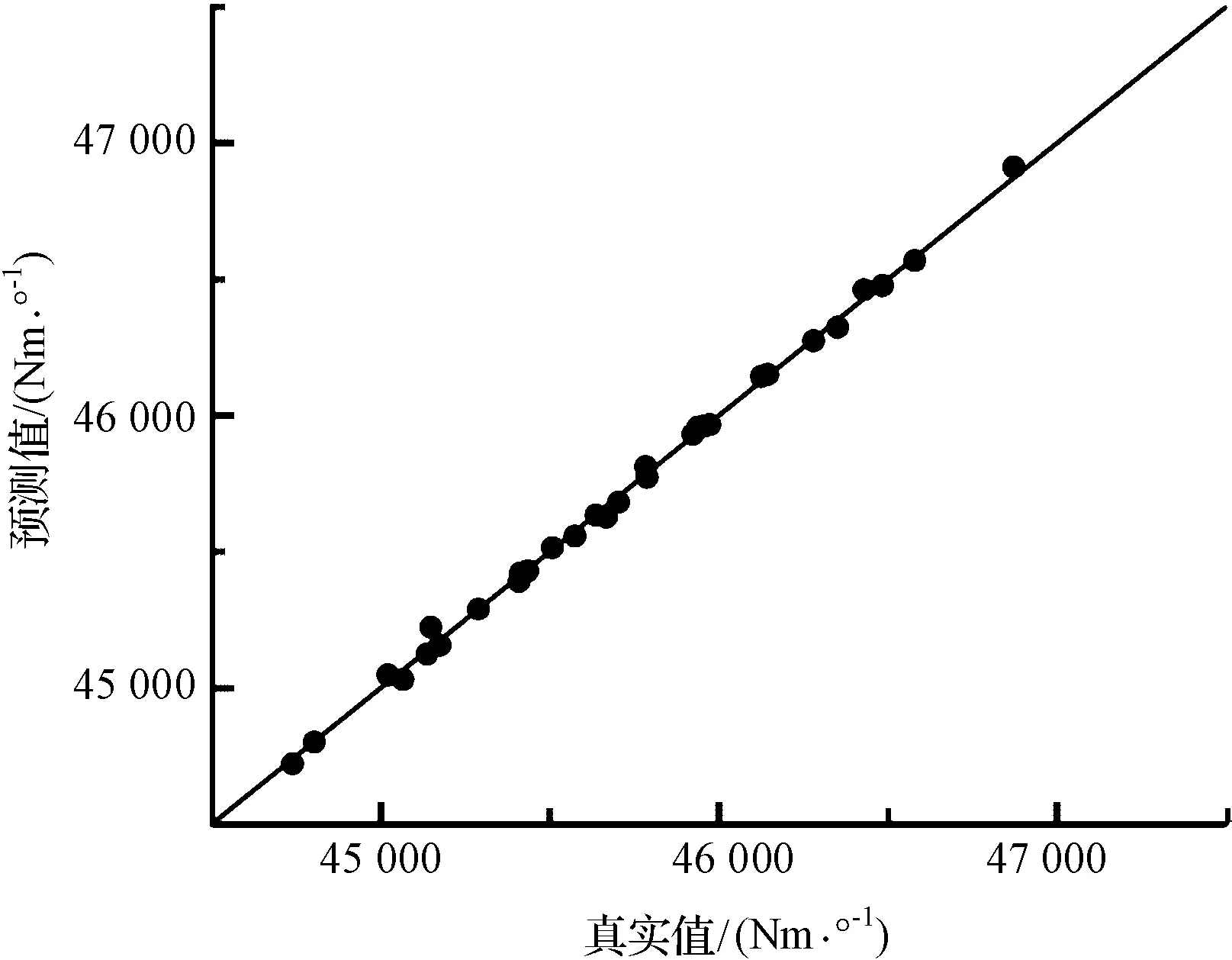
图10 扭转刚度拟合精度误差散点图•—进行误差分析的样本点,样本点越贴近倾斜直线表示指标拟合精度越高
4 优化仿真
4.1 优化算法
在工程实践中往往需要同时优化多个相互冲突的目标,而进化算法是解决多目标优化问题最有效的方法。现有的研究成果表明[16],对于2~3个优化目标的多目标优化问题,第二代遗传算法可以得到收敛性、多样性较好的pareto解集。
上述优化问题共3个目标,即质量最小、弯曲刚度最大、扭转刚度最大。使用传统单目标优化算法并不能很好解决问题,故笔者选择第二代遗传算法。
4.2 优化问题描述
此次优化选取梁截面形状Sn(n=1,2,…,45)、厚度Tn(n=1,2,…,33),共78个设计变量;约束条件为一阶扭转模态频率≥21 Hz、一阶弯曲模态频率≥39.5 Hz,以质量最小、扭转刚度最大、弯曲刚度最大为优化目标。
优化问题的数学描述为:
Variable:T=(T1,T2,…,T33),S=(S1,S2,…,S45)
Objective:{Mmin(S,T),FTmax(S,T),FBmax(S,T)}
s.t.fTMmin≥21;fBMmin≥39.5
(10)
式中:Mmin—质量最小值,kg;FTmax—扭转刚度最大值,Nm/°;FBmax—弯曲刚度最大值,N/mm;fTMmin—一阶扭转模态频率最小值,Hz;fBMmin—一阶弯曲模态频率最小值,Hz。
4.3 结果分析
笔者采用第二代遗传算法,对商用车驾驶室进行了多目标优化。优化前后性能值如表6所示。
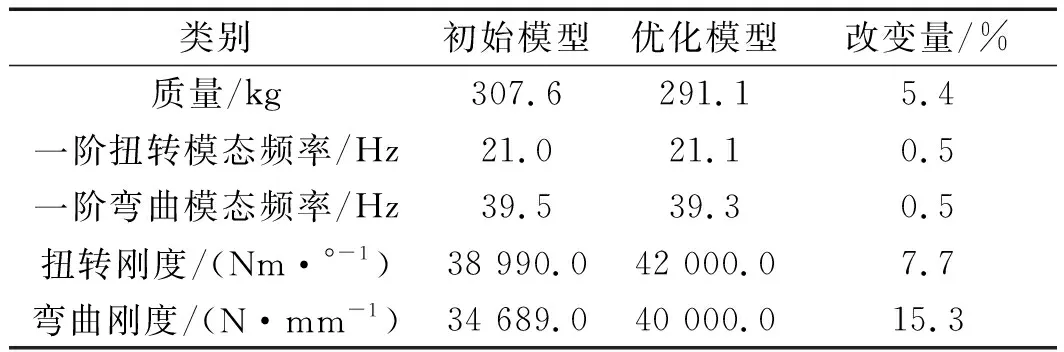
表6 优化前后性能值
由表6可知:优化后驾驶室的质量下降16.5 kg,下降幅度5.4%;扭转刚度提升了7.7%,弯曲刚度提升了15.3%,一阶扭转模态频率提升了0.5%,一阶弯曲模态频率降低了0.5%;
由此可见,在低阶振动频率基本不变的情况下,驾驶室质量下降,扭转刚度、弯曲刚度均有较大提升,多目标优化效果较佳。
5 结束语
本研究利用SFE-Concept软件构建了商用车驾驶室隐式参数化模型,并完成了模型精度验证,之后采用比例向量法控制梁截面形状,然后结合有限元前处理软件进行了灵敏度分析,最后构建了混合近似模型,并进行了多目标优化。
研究结果表明:
(1)相较于传统优化方法,采用隐式参数化模型进行的商用车驾驶室梁截面优化,扩大了优化算法的寻优空间,增加了算法寻到最优解的几率;
(2)通过研究驾驶室梁的截面力学特性,找出了梁截面的控制因素(截面形状、厚度),利用比例向量法用较少变量控制梁截面形状,减少了优化变量数量;
(3)提出了通过结合HyperMesh、HyperMorph分别进行驾驶室厚度灵敏度分析、梁截面灵敏度分析的方法;相较以试验设计进行灵敏度分析的方式,该方法试验设计时间缩短了40%,优化效率提高;
(4)构建了径向基—响应面混合近似模型,以提升近似模型拟合精度,使驾驶室性能指标的相关系数值都在0.9以上,达到了精度要求;
(5)采用第二代遗传算法,对该问题进行多目标优化,优化结果表明,在固有低阶振动频率基本不变的情况下,驾驶室质量下降16.5 kg,减幅5.4%,弯曲刚度提升了15.3%,扭转刚度提升了7.7%,多目标优化效果较佳。
目前,该研究还存在一些不足,如利用比例向量法控制截面形状时,并未给出选取θ=0°进行研究的原因。在后续的工作中,笔者还将就此问题进行进一步的研究,以更科学地确定旋转角度的取值。
