基于谱方法的柔性悬架系统高效动力学仿真*

李晓飞,李海艳,梁桂铭

(广东工业大学 机电工程学院,广东 广州 510006)

0 引 言

车辆悬架系统受到多种作用力,其对车辆系统动力学性能影响非常大,所以建立悬架系统动力学模型并进行仿真是研究车辆系统动力学性能的重要工作之一。

车辆的悬架系统属于柔性多体系统范畴,其柔性梁在运动时存在大位移的刚性运动,同时产生一定的弹性变形运动,这两种运动是高度耦合的[1]。在悬架系统的动力学建模中,由于弹性变形有无限维自由度的特点,其精确解无法求得。目前处理弹性变形的方法一般是将其在时间和空间方面离散,求取其近似解[2]。常用的离散方法有3种,即有限单元法、假设模态法和谱方法。

其中,有限单元法是在空间上将柔性体划分成网格单元,通过求解网格单元的变形近似弹性变形的精确解。PATIL A M等人[3]使用有限元方法,建立了悬架系统静止状态下的动力学模型。GADADE M B等人[4]针对商用车前下悬架臂的设计问题,研究了静止状态下的悬架系统三维有限元动力学模型。NABAWY A E等人[5]使用平面杆单元,建立了一种悬架系统综合的有限元模型,研究了双叉梁悬架系统的动态响应。

依据有限单元法离散求解了柔性体弹性变形,虽然保证了求解精度,但是其划分网格单元较多,使得其计算量非常大,计算效率低。

而采用假设模态法时,需通过先验知识求得柔性体的模态和振型,然后根据精度要求决定截断振型函数的阶数,再通过振型拟合柔性体的变形。VAKIL M等人[6]使用假设模态法建立了柔性连杆动力学模型,并分析了其动力学模型的可行性。潘云[7]采用假设模态法,建立了柔性机械臂的动力学模型,并对机械臂的轨迹控制进行了研究。张晓宇等人[8，9]依据假设模态法,建立了柔性连杆的动力学模型,研究了其对控制器设计的影响。

虽然采用假设模态法拟合弹性变形函数比较简便,但是其所增加的振型函数的项数会产生计算效率急剧降低的问题。

谱方法[10]是通过一组正交多项式的有限级数来表示柔性体弹性变形。它无需对网格进行划分,也不需要先验知识处理弹性变形函数的拟合,具有收敛快、高精度的特点。

基于上述原因,笔者将谱方法引入到柔性多体动力学建模中,将巴哈赛车悬架系统中柔性梁的弹性变形函数离散成Chebyshev多项式的有限级数形式,通过置换方法处理弹性变形函数,再利用弹性变形函数和拉格朗日动力学公式建立悬架系统的柔性多体动力学模型,通过广义α方法[11]进行迭代求解;最后将计算结果与其他方法进行对比,验证基于谱方法的悬架系统动力学建模求解的准确性和高效性。

1 悬挂系统解耦与柔性梁运动描述

巴哈赛车模型如图1所示。

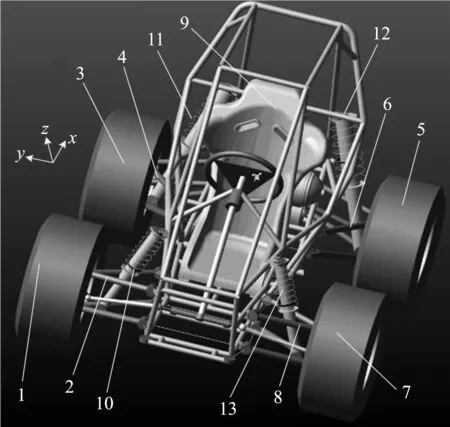
图1 巴哈赛车模型1,3,5,7—轮胎;2,4,6,8—柔性梁;9—车架;10,11,12,13—减震器

为了便于对悬架系统进行建模,笔者依据浮动框架建立悬架系统的坐标系,即以初始状态车架的重心o为原点建立oxyz绝对坐标系,然后以运动部件i(i=1,2,…,9)的重心oi为局部坐标系原点,建立初始状态与绝对坐标系平行的局部坐标系oixiyizi;

由于悬架系统左右对称,笔者依据文献[12]的悬架解耦控制方法,将悬架系统解耦成4个1/4悬架和1个受到4个弹簧阻尼力的车架系统,整个悬架系统按5部分进行动力学建模,再利用其作用力之间的关系形成完整的动力学模型。

接下来,笔者对1/4悬架系统进行分析。

1/4悬架系统原理图如图2所示。

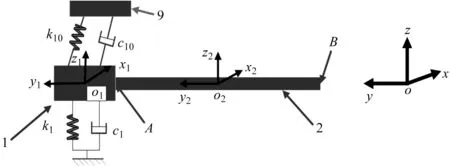
图2 1/4悬挂系统k1,k10—弹簧阻尼器1,10弹性系数;c1,c10—弹簧阻尼器1,10弹性系数

笔者将减震器简化成弹簧阻尼器10,将轮胎1简化成刚体1和弹簧阻尼器1。由于柔性梁2的长度远大于其截面的直径,柔性梁的截面方向的变形变化非常小,其中心线的变形可比较精确地表示截面的变形,柔性梁可简化为空间梁结构。

笔者依据图2对柔性梁2进行运动分析。

柔性梁2上某一点p的位移矢量为:

r2=R2+A2u2=R2+A2(u20+u2f)

(1)

式中:R2—点o2在绝对坐标系oxyz上的位移;A2—柔性梁2的旋转矩阵;u20,u2f—点p在局部坐标系o2x2y2z2上的刚性位移和弹性变形位移。

2 基于谱方法的动力学建模

2.1 柔性梁弹性变形表示

根据柔性梁2的运动描述可知,柔性梁2的位移由刚性位移与弹性变形位移叠加而成。因此,柔性梁2的弹性变形位移可表示为:

(2)

式中:u2fx,u2fy,u2fz—弹性变形在x2,y2和z2轴上的投影。

笔者依据谱方法将弹性变形位移函数进行离散,将空间项和时间项分离,得到有限级数表达式:

(3)

式中:Tm(y)—区间[-L2/2,L2/2]上的第一类切比雪夫多项式;a2m(t),b2m(t),c2m(t)—对应的谱表示系数;L2—柔性梁2长度;M—多项式截断数。

将弹性变形函数写成矩阵表示形式,即:

u2f=U2fqU2+V2fqV2

(4)

其中:

(5)

(6)

(7)

由于根据谱方法得到的柔性梁2弹性变形位移函数需要满足相应的边界条件,需要对弹性变形位移函数进行置换处理。

柔性梁2上点A为固定连接,点B为铰接,所以u2fx,u2fy,u2fz需要满足如下边界条件:

(5)

将式(8)写成矩阵形式,即:

U2qU2+V2qV2=0

(9)

其中:

(10)

根据式(9),qV2可以表示为:

(11)

将式(11)中的qV2置换代入式(4),可得:

(12)

式中:u2f—满足边界条件的谱表示弹性位移函数;S2f—谱表示弹性位移函数的形函数;qU2—谱表示弹性位移函数的广义坐标。

2.2 动力学模型

根据式(1,12)所求得的柔性梁2的谱表示弹性位移函数u2f,形函数S2f和弹性变形广义坐标qU2,可得柔性梁2的谱表示的位移矢量为:

r2=R2+A2(u20+S2fqU2)

(13)

依据位移矢量r2,对t求微分得到速度矢量,可将柔性梁2的动能[13]表示为:

(14)

式中:ρ2—柔性梁2的密度;M2—质量矩阵;V2—柔性梁2的三维可行域;“·”—对时间t微分。

其中:

(15)

式中:θ2—局部坐标系o2x2y2z2中x2、y2、z2轴与绝对坐标系oxyz中x、y、z轴的夹角向量。

将式(14)代入拉格朗日方程可得:

(16)

经整理可得谱表示的柔性梁2的运动方程为:

(17)

式中:Cq2—雅克比矩阵。

其中:

(18)

(19)

式中:D—三维弹性矩阵。

因为柔性梁2所受外力只有重力,所以广义外力Q2e可通过虚功原理[14]求得,即:

(20)

式中:g—重力加速度;δq2—虚位移。

由于车轮1简化为刚体1与弹簧阻尼器1,其刚体1运动方程为:

(21)

式中:M1—刚体1的质量矩阵;R1—刚体1的质心坐标。

其中:

(22)

式中:θ1—局部坐标系o1x1y1z1中x1、y1、z1轴与绝对坐标系oxyz中x、y、z轴的夹角向量。

由于刚体1所受的外力为弹簧阻尼力和重力,且作用于质心,其广义外力Q1e为:

(23)

其中:

(24)

式中:γ—弹簧阻尼器10与z轴的夹角;u9z—车架的在z9轴的位移;β9—车架关于y9轴的转角;La—车架质心在x轴向与弹簧阻尼器10的距离;Rf—地面激励。

根据式(17,21)可得1/4悬架系统动力学方程为:

(25)

由于广义坐标q1与q2受约束影响而不完全独立,Cq12需要根据柔性梁2与车轮1的约束方程求得。

柔性梁2与车轮1在点A为固定连接,在点B与底盘铰接,其对应的约束方程为:

(26)

式中:u1A,u20A—点A在局部坐标系o1x1y1z1和o2x2y2z2上的初始位移;S2fA—点A在局部坐标系o2x2y2z2上的形函数;S2fB—点B在局部坐标系o2x2y2z2上的形函数;RcB—点B在全局坐标系oxyz上的位移。

将式(26)表示为:

Φq12=0

(27)

雅克比矩阵Cq12和加速度右项Qc12可由文献[15]中的公式求得,即:

(28)

式中:“‥”—对t的二阶微分。

由于车架与车轮是通过弹簧阻尼器连接,车架运动只与外力有关,且车架为刚体,其动力学方程为:

M9q9=Q9e

(29)

式中:M9—车架的质量矩阵;q9—广义坐标。

由于悬架系统[16]左右对称,车架受到的外力为弹簧阻尼力和重力,Q9e为:

(30)

其中:

(31)

(32)

式中:Lb—车架质心在x轴向与弹簧阻尼器11的距离;k11,k12,k13—弹簧阻尼器11-13的弹性系数;c11,c12,c13—弹簧阻尼器11-13的阻尼系数;ujz—车轮j(j=1,3,5,7)的z轴的位移。

同理,通过式(25),可求其他1/4悬架系统的动力学方程,然后根据所求得的悬架系统动力学方程和车架的动力学方程,依据广义坐标,可形成整车悬架系统的动力学模型。

将其与约束方程整理成矩阵形式为:

(33)

3 数值仿真及分析

3.1 广义α方法迭代求解

悬架系统参数[17]如表1所示。

表1 悬架系统参数

为了验证基于谱方法的悬架系统动力学模型的可行性和高效性,笔者利用表1中的参数对其进行仿真求解。

通过广义α方法的仿真求解流程如图3所示。

图3 仿真流程图

具体仿真流程为:

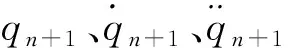
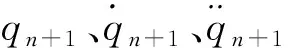
由于流程图3中其他参数和变量相应文献有详细描述和具体计算公式,此处不再赘述。

3.2 与有限元动力学模型的车架位移对比

笔者将仿真的车架位移与求解三维有限元动力学模型得到的车架位移相对比。

其中,车架z轴位移如图4所示。

图4 车架z轴位移

车架y向转角如图5所示。

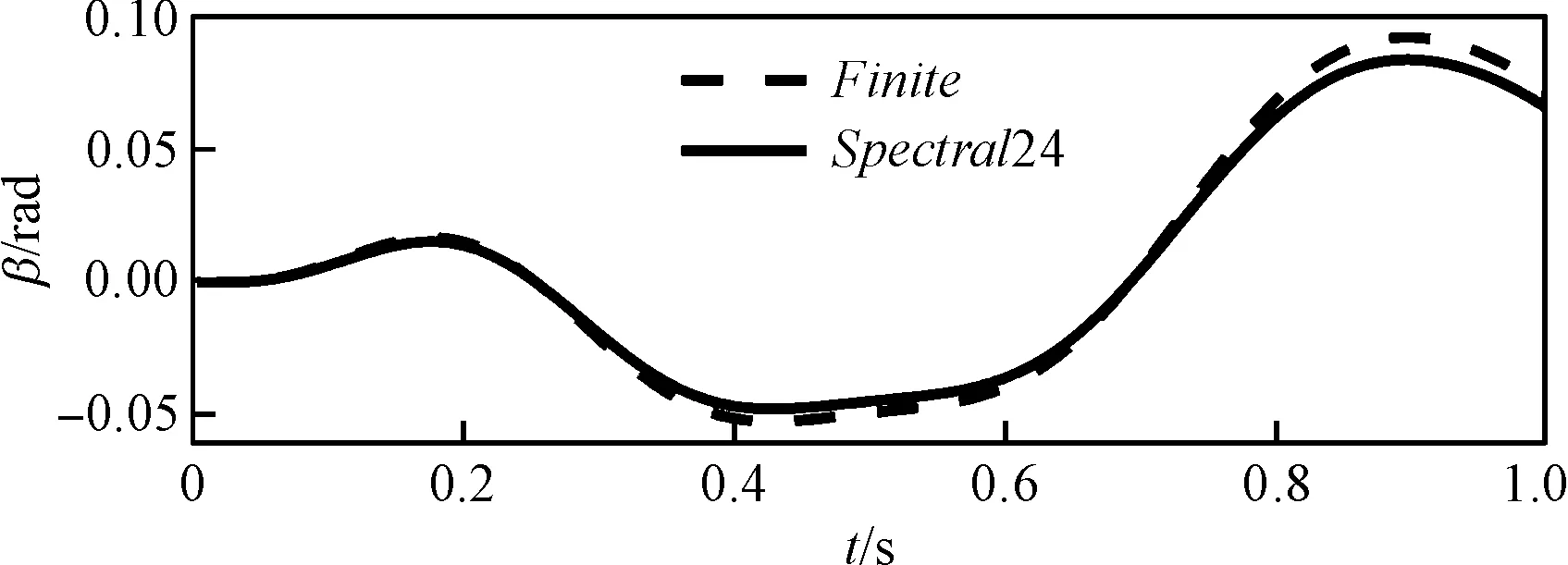
图5 车架y向转角

通过二范数可计算其相对误差ζ:

(34)

式中:DF—精确解;DS—试验解。

以有限元的仿真的车架位移为精确解DF,基于谱方法动力学模型的车架位移为试验解DS,车架z向位移二范数相对误差为3.57%,y向转角的二范数相对误差为3.37%。

该结果表明:基于谱方法的悬架系统动力学模型的误差在可容许范围内。

3.3 与有限元动力学模型柔性梁弹性位移对比

根据仿真迭代求出的广义坐标q和已知的弹性变形的形函数Sjf(j=2,4,6,8),可求出柔性梁j的弹性变形。

笔者将不同Chebyshev多项式阶数下,基于谱方法的动力学模型仿真求得的柔性梁弹性变形位移,与有限元动力学模型求解得到的不同时刻下弹性变形位移相对比,结果如图(6～11)所示。

图6 柔性梁2的x向弹性位移

图7 柔性梁2的y向弹性位移

图8 柔性梁2的z向弹性位移

图9 柔性梁4的x向弹性位移

图10 柔性梁4的y向弹性位移

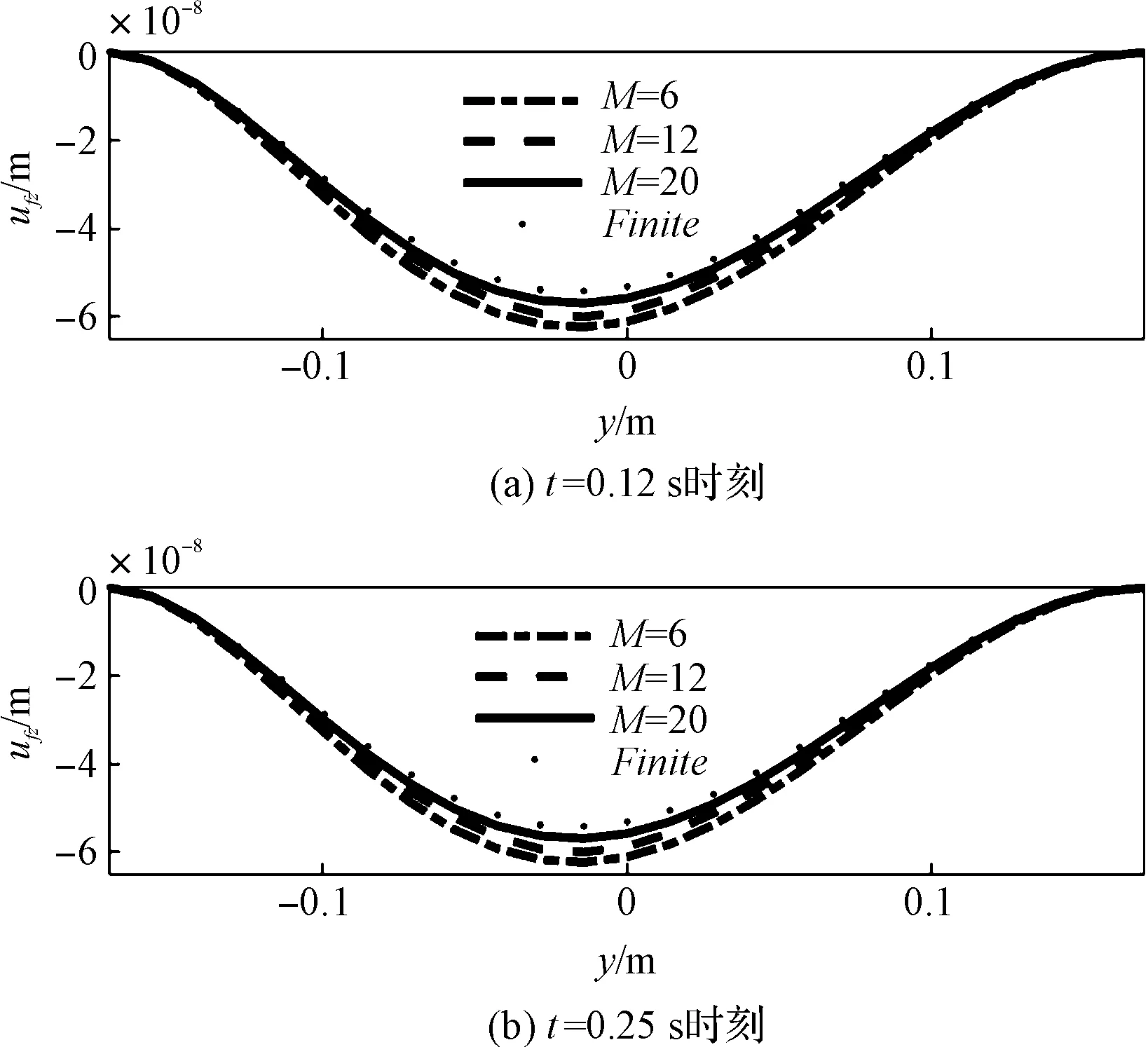
图11 柔性梁4的z向弹性位移

接着,笔者以有限元动力学模型求解出的柔性梁弹性位移为准确值,以基于谱方法动力学模型计算出的柔性梁弹性变形为试验值,通过式(34)计算弹性变形二范数相对误差,结果如表2所示。

表2 不同阶数下的柔性梁相对误差

根据表2的数据和图(6～11)的结果可得:

(1)随着谱方法选取Chebyshev多项式项数的增加,笔者所提的方法的计算精度不断提高,当所取Chebyshev多项式项数为24时,柔性梁弹性变形最大相对误差为1.18%;

(2)随着所取Chebyshev多项式项数增加,相对误差最大值的递减幅度越来越小,当所取多项式项数达到16时,继续增加多项式项数相对误差降低幅度已经不显著,最大降低幅度为0.54%;

(3)表2所示的时间为在相同计算机软件与硬件条件下,悬架系统动力学模型的求解时间;依据表2中的数据可知,随着所取Chebyshev多项式项数递增,求解总时间也在依次递增;

(4)当振型函数和Chebyshev多项式都取24阶时,假设模态法动力学模型求解时间是基于谱方法的悬架系统动力学模型求解计算时间的4.896倍。

4 结束语

笔者采用谱方法将悬架系统中柔性梁的弹性变形函数离散成Chebyshev多项式的有限级数形式,通过置换方法处理弹性变形函数得到的边界条件,再利用弹性变形函数和拉格朗日动力学公式建立悬架系统的柔性多体动力学模型,通过广义α方法迭代求解,最后将基于谱方法的悬架系统动力学模型的求解结果与其他方法下悬架系统动力学模型求解结果进行对比,得到了以下结论:

(1)将基于谱方法的悬架系统动力学模型的求解结果与有限元动力学模型仿真的求解结果相对比,车架位移的相对误差为3.57%,柔性梁的弹性变形相对误差最小为1.18%;

(2)当振型函数和Chebyshev多项式都取24阶时,基于谱方法的悬架系统动力学模型的计算效率是假设模态法动力学模型计算效率的4.896倍,体现了谱方法的高效性;

(3)当所取Chebyshev多项式项数达到16时,继续增加阶数,基于谱方法的悬架系统动力学模型的计算精度提升不大,计算效率降低比较多,所以在动力学建模中需要适当地选取Chebyshev多项式项数。

目前谱方法使用的正交多项式是考虑截断其前M项,不是有选择性地挑选正交多项式中的项。因此,在后续的研究中,笔者将通过压缩感知稀疏理论,有选择性地挑选正交多项式中项,来拟合待求函数,以进一步提升其计算精度和效率。