集成学习在电网假数据入侵检测中的应用
2022-02-24戚元星崔双喜
戚元星,崔双喜
(新疆大学 电气工程学院,新疆 乌鲁木齐 830047)
目前,时代进步促进信息和科技的高速发展,高速通信和高度集成的信息网络成为了电力系统的重要支撑.在电网中,攻击者为了达到破坏电网正常运行、误导控制中心操作、获取不正当利益的目的,会选择对电网的数据采集与监视控制系统(supervisory control and data acquisition,SCADA)进行攻击.电力系统的采集单元覆盖电网的全拓扑,所以,攻击者会把预先设定的攻击向量注入到采集单元中,为了不被电网检测模块检测出来,攻击者会制造最优攻击向量来躲避检测模块检测.虚假数据的攻击会造成依赖电网行业不同程度的瘫痪,给国家、社会、人民带来很大的危害,因此对于虚假数据检测的研究显得尤为重要[1-4].传统的电网虚假数据检测有很多[5-7],比如用核范数最小化或低秩矩阵分解对虚假数据进行检测[8].机器学习的发展也为虚假数据的检测提供了新的方案,最典型的有3种实现方式:监督学习、半监督学习和无监督学习[9],其中监督学习的分类技术最为优秀,预测精度高且整体效果较好,但需要完整的带标签的样本,数据的质量和数量决定最终的模型效果.集成学习作为机器学习的重要部分,也逐渐被应用于入侵检测领域[10-13],现有实验结果表明运用机器学习中的单分类器来检测虚假数据会出现准确率低以及模型区分能力差等问题,因此,针对该类问题结合虚假数据检测原理,本文提出一种新的集成学习检测方法并对其可行性进行验证,实验结果表明本文在电网虚假数据检测分类问题上具有一定研究价值.
1 系统模型
1.1 虚假数据攻击模型
对于含有n个状态量的向量x=[x1,x2,x3,…,xn]以及m个量测值的向量z=[z1,z2,z3,…,zm],两者之间的关系为
z=Hx+e,
(1)
(2)
其中,H表示为直流维度模型m×n的雅克比矩阵,e为误差.
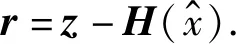
(3)
1.2 虚假数据注入攻击向量构建
对于标准的直流系统,只考虑带相位角的状态变量,直流系统线路电阻可忽略不计,直流系统电压幅值全部设为 1,本文攻击前的量测值样本采用的是IEEE14节点14个标准的母线负载有功功率,20个分支路首端有功功率,20个分支路末端有功功率,一组攻击前的样本共54个状态变量.攻击后的量测值za如式(4),攻击后的状态变量xa如式(5)
za=Hx+a+e,
(4)
xa=x+a,
(5)
其中,a为攻击的向量;e为量测的误差.
第j个子区域攻击后状态估计的残差、全部域攻击后的状态估计的残差如式(6)、(7)所示
(6)
(7)
为了构造出最优的电网虚假数据攻击向量,使虚假数据逃避电网检测模块检测,应让攻击后的残差值处在电网虚假数据检测阀值以内,在满足式(8)条件下求式(9)最优解
(8)
(9)
β为优化量,λ为正则化参数,j=1,2,…,n.
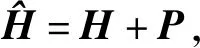
(10)
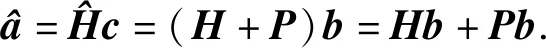
(11)
当且仅当
Pb=0时,
(12)
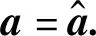
(13)
由式(12),求电网SCADA系统注入虚假数据向量b残差最小的最优解函数
(14)
bj-θ=0,
(15)
θ为优化变量,λ为正则化参数,j=1,2,…,n.
根据式(14),可求非全部网络拓扑雅克比矩阵虚假数据攻击的注入向量.
2 虚假数据攻击检测模型
2.1 基于GBDT的攻击检测模型
梯度提升树(gradient boosting decison tree, GBDT)由决策树和梯度提升组合而成,可处理大部分的分类回归任务.
在GBDT的迭代过程中,初始化基学习器F0(x),对数损失函数L(y,F(x)),如下所示:
(16)
L(y,F(x))=log(1+exp(-2yF(x))),
(17)
β为损失函数最小化的常数值.
设迭代数量为m,为进一步拟合本轮损失,需得到损失函数的数值
(18)
损失函数梯度下降最优步长βnm
(19)
定义学习率为ν∈(0,1],进一步构建更高精度的弱分类器模型Fm(x),
(20)
迭代结束后,得到由m个高精度的弱分类器结合的决策树模型
(21)
2.2 基于XGBoost的攻击检测模型
XGBoost使用一阶导数和二阶导数,对代价函数进行泰勒展开,为了使模型简单化,加入了正则项Ω.本文使用表示第i个叶子节点上的分数.为了学习出模型参数,对目标函数正则化,公式如下:
(22)
(23)
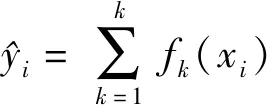
经对损失函数的一阶梯度和二阶梯度,再去掉常数项并展开Ω,得到的目标函数
(24)
(25)
(26)
树结构选择增益下降最大的特征作为最优分割点,增益下降的公式为
(27)
2.3 基于LightGBM与基于RF-LightGBM的攻击检测模型
LightGBM是在GBDT的算法的基础上进行改进.LightGBM解决了在大样本高维度数据出现的耗时且耗内存问题.该算法改进了2个方面:gradient-based one-side sampling(GOSS)和exclusive feature bundling(EFB).互补特征压缩(EFB)通过将相近的特征进行合并达到2种目的:1)使特征维度从高维变为低维来寻找最优分割点;2)使降维对数据特征的损失最小.对实例进行采样时,基于梯度的单面采样(GOSS)是为保持信息增益的准确保留较大贡献的实例,删除一部分小梯度的样本.
RF-LightGBM是在LightGBM攻击检测模型的基础上,对需要检测的样本数据集先采用随机森林(RF)对特征值进行重要性排序.通过去除没有必要的特征来降低模型训练时间及升高模型的准确度.随机森林结合多个决策树,每个决策树的建立取决于独立提取样本,不纯度和袋外数据错误率决定最佳分裂节点,对于决策树森林可以计算出每个特征减少的树的不纯度,并作为特征选择的值.
2.4 基于Bagging的攻击检测模型
Bagging的决策树算法通过对原始数据随机采样,并选择信息增益为计算指标进行分类,根据方差和偏差对分类结果进行优化.该算法的特点是各个决策树之间没有依赖关系,每个基模型可以分别、独立、互不影响地生成并且拟合.
Bagging算法的集成过程如下所示.
Input: Data setS={(x1,y1),(x2,y2)...(xn,yn) }
Process:
Fork=1,2,…,K
Sk=Bootsrap(S)
hi=L(S)
H(x)=H(hi)
End
ReturnH(x)
2.5 多分类器集成模型
本文分别训练多个优秀的分类器:gradient boosting decision tree(GBDT)、XGBoost、lightGBM、RF-LightGBM、Bagging.检测训练好的分类器是否符合要求,用测试样本集对训练好的各分类器进行测试.最后,把多个分类器合并成一个集强分类器,在采用软投票的方法综合不同分类器的检测概率,使整个数据集的情况可以较全面地反映出来,原理如图 1所示.
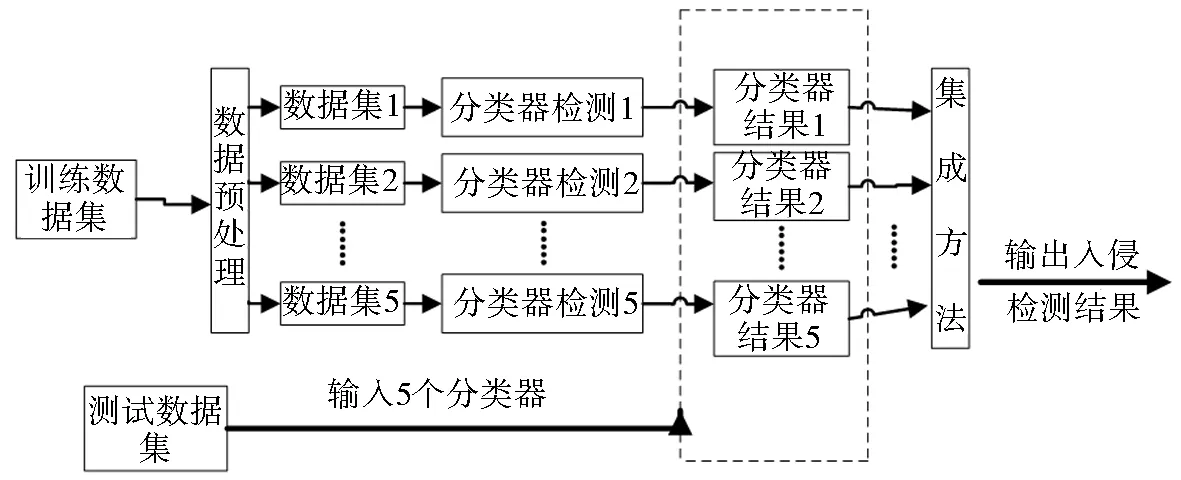
图1 多分类器集成学习入侵检测原理Fig.1 Principle of multi classifier ensemble learning intrusion detection
基于集成学习的入侵检测的算法
输入:样本数据集S.
输出:检测结果.
1)将样本数据集S按照1∶1划分为2部分,得到训练集S1和测试集S2;
2)用python标记好的数据集NT;
3)Foriin
S1进行转换→带标签的Si
Si分别输入到LightGBM,RF-LightGBM,XGBoost,gradient boosting decision tree(GBDT), Bagging进行训练→分类器i;
4)Forjin;
S2输入分类器j→概率j;
5)用软投票机制对多个分类器的概率结果进行集成得到强分类器,T为分类器数量,hi(x)为分类器检测概率
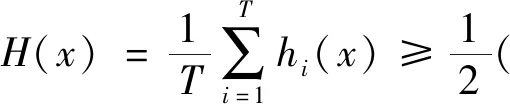
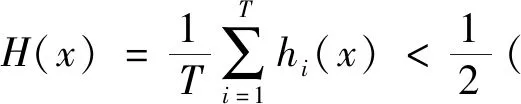
6)Return检测结果
2.6 贝叶斯调参模型
模型选择的特征决定模型的性能上限,而参数调优使模型更接近这个上限,在模型的准确度与复杂度之间寻找平衡,防止模型过拟合并提高鲁棒性.贝叶斯调参的基本思想:在贝叶斯定理下,用先验数据估计目标函数的后验分布,然后再根据后验分布来确定下一个最优先验数据进而确定超参数组合.调参步骤如下:
1) 确定初始学习速率0.15,估计treebased参数调优数目;
2) 控制树的数量(nestimators)来提高模型的速度;
3) 对树的最大深度(max depth)和最小叶子节点样本权重(min child weight)参数调优,对比模型分类的错误率,防止模型过拟合;
4) 调整subsample,使每棵树采样的比例适中;
5) 降低学习速率,待模型基本收敛,停止迭代.
3 仿真实验
3.1 数据集描述
在标准 IEEE14-bus节点系统中假设攻击者已知局部网络拓扑雅克比矩阵的前提下,注入虚假数据向量b进行攻击,攻击电网SCADA系统网络成功后,可在 Python环境下进行:标注受到攻击量测值标注为0,未受攻击量测值标注为1,构建了10 000个样本数据集:8 000条训练样本和2 000条测试样本.数据样本集D,攻击检测数据样本X,样本类标记Y,如下所示:
D={X,Y}={(x1,y1),(x2,y2),…,(x1000,y1000)},
X=(x1,x2,…,x1000),
Y=(y1,y2,…,y1000∈{0,1}
.
(28)
3.2 贝叶斯调参结果
在 Python环境下,先使用测试集对训练好的5种分类器进行测试:LightGBM、RF-LightGBM、XGBoost、gradient boosting decision tree、bagging,使用贝叶斯进行调参,电网假数据检测集成学习模型是由几个基分类器合并而成的,因此需要对其中的LightGBM、RF-LightGBM和XGBoost这3个基分类器进行调参.
LightGBM、RF-LightGBM和XGBoost参数范围为:设置树的数量(1,100),最小叶子节点样本权重(1,20),树的最大深度(2,20),subsample(0.1,1),贝叶斯调参采用高斯过程,考虑之前的参数信息,不断更新先验来比较模型运行的时间,分类错误率等指标,判断模型是否收敛,经过不断测试模型迭代到20次左右已经基本收敛.
最后,选择的模型参数如表1、表2、表3所示.

表1 LightGBM模型参数Tab.1 LightGBM model parameters

表2 RF-LightGBM模型参数Tab.2 RF-LightGBM model parameters

表3 XGBoost模型参数Tab.3 XGBoost model parameters
3.3 虚假数据检测结果
将本文5种分类器分别对数据集样本进行检测,通过对虚假数据检测结果的评估指标分析 ,各分类器之间不仅可以做对比还是集成模型中的基分类器.评估指标如下:分类器模型能力度area under ROC(AUC)、查确率 average precision (AP)、准确率balanced accuracy (BA)、 平均几何正确率G-mean、服从正态分布度KS-Value,上述指标均是越高越好,误检率false detection rata (FDR)越低越好.
1)根据表4和表5中模型对虚假数据检测的各评估指标百分比,为更直观的表达各分类器及优化后集成模型中每个评估指标之间差异,画出了各分类器每个评估指标之间的对比图,如图2所示,其中纵坐标为评估指标的百分比,横坐标为各评估指标.

表4 各分类器评估指标Tab.4 Evaluation index of each classifier
以本文以上阶段所得到的基分类器为主,使用软投票策略集成基分类器的决策,构建一个新的集成模型.

表5 优化后集成模型的评估指标Tab.5 Evaluation index of optimized integration model
2)当 AUC 为 0.5时,即代表模型的区分能力与随机猜测能力一致;当 AUC 值越高其模型能力越强. 由表4和表5知,关于优化后集成模型分类器的模型区分能力(AUC)高达93.12%. 从图2不难看出,优化后集成模型的区分能力是本文提到的几种分类器最好的,说明此模型的检测虚假数据能力可信度较高. 由图2也可以看出AP、BA、G-mean、KS-Value的指标是这几个分类器最高的,尤其是优化后集成模型的查准率(AP)高达91.68%,准确率(BA)高达90.91%,误检率(FDR)为7.09%,比单个分类器检测的查准率提升了至少11%,准确率提升了至少9%,误检率降低了至少5.22%,说明由5种基分类器集成的模型具有较好的检测效果,进一步说明了检测模型泛化能力也得到了进一步提升,在入侵检测中,误检率带来的损失较大,因此,研究人员都期望在能够保证提升查准率、准确率的情况下,使误检率尽可能低,这样更符合实际应用的要求.
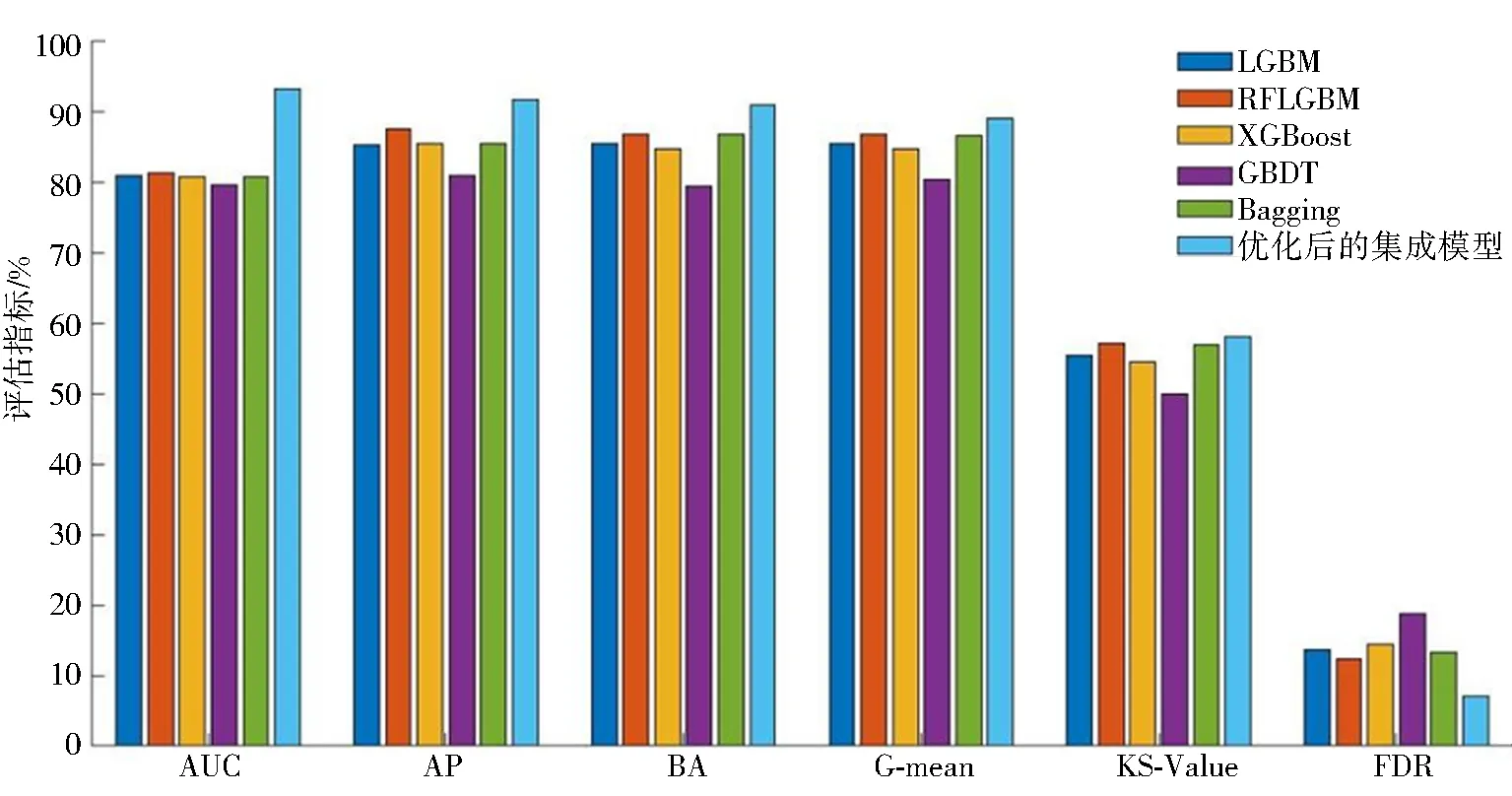
图2 各分类器评估指标对比Fig.2 Comparison of evaluation indexes of each classifier
为了进一步检测优化后集成模型的分类效果,本算法与2种经典分类算法做了对比,分别是扩展卡尔曼滤波算法和与主成分分析结合的支持向量机(PCA+SVM),如图3所示.在不同样本数的情况下,随着样本数增多,本算法的准确率大多高于PCA+SVM算法的分类准确率,但是图3中也存在准确率优于本算法,主要原因在于数据集预处理上对选取样本的随机性造成的样本集的差异,这种差异是每种算法对样本数划分的划分标准不同而导致的.而扩展卡尔曼滤波检测算法除了存在小样本数据集上的准确率会略高于本算法,但绝大多数的样本集分类效果不如本算法,其原因是扩展卡尔曼滤波检测算法在真假数据不平衡的样本集中,其分类准确率会随样本数的增多而降低.
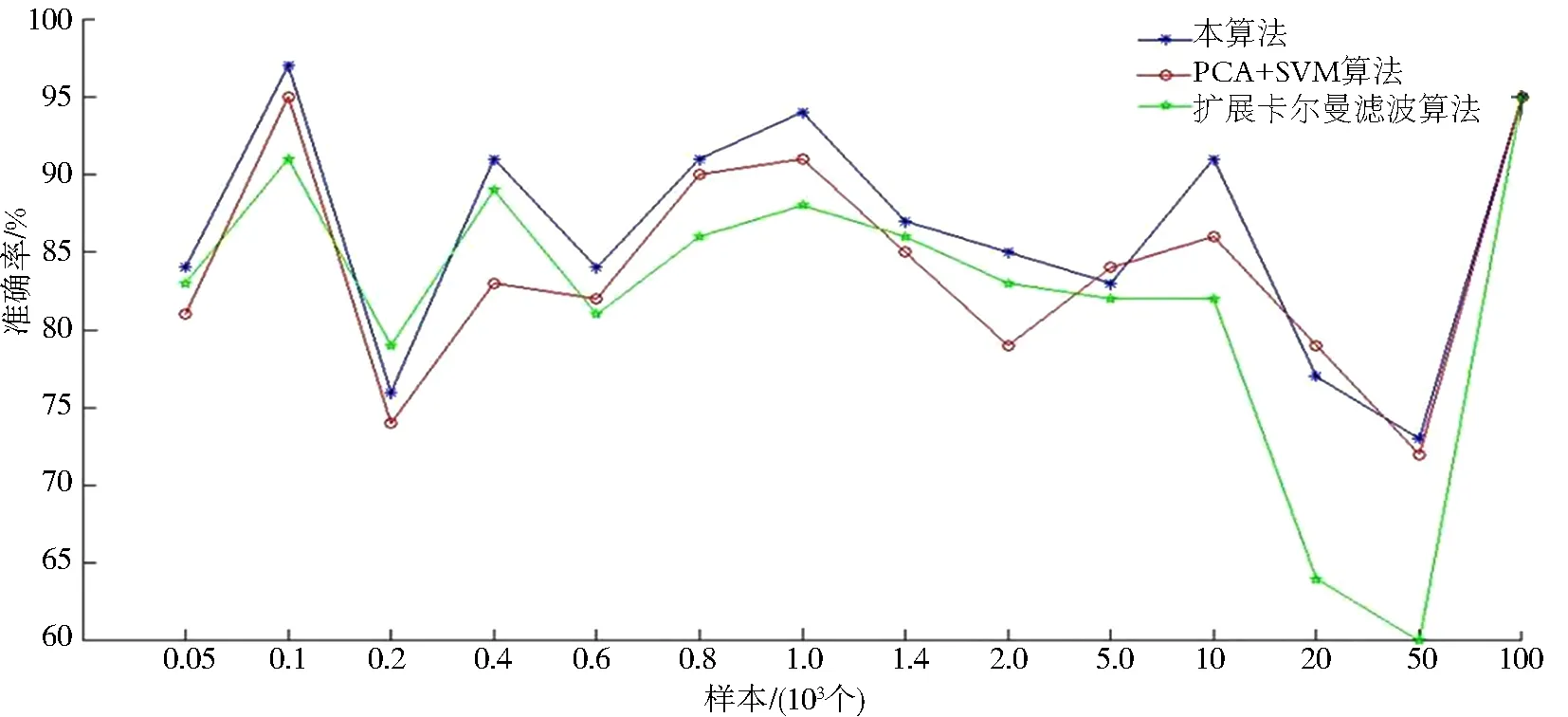
图3 准确率对比Fig.3 Comparison of accuracy
4 结语
本文基于集成学习算法对电网假数据进行检测,经仿真实验,该算法在解决单分类器检测查准率和准确率不高和单分类器检测不稳定问题基础上,可有效提高对电网虚假数据的检测能力,比采用传统的检测算法查准率和准确率有明显提升.此外,该检测算法在检测电网假数据的应用上也是创新.在保证各项评估指标较好的前提下再次提高检测精确率和降低误检率将成为下步研究方向和工作.
