基于衍射理论定量研究衍射调节与振幅误差

路彦珍,张腾远,王泽宇,王凤平

(北京科技大学 数理学院, 北京 100083)

光的衍射是波动光学中的重要组成内容,在物理学中有着重要地位，其中夫琅禾费衍射与菲涅尔衍射是光的衍射中常用的分析方法和应用领域.根据查阅文献内容可以得知这2种衍射的光强与振幅分布、衍射图样、衍射模型分析方法等[1-3].根据此理论,波带片与光栅等光学元件在工程中有着重要的应用,但在分析过程中常有近似条件,忽略部分因素便于分析结果,如果不能选择合适的近似条件容易造成较大误差.目前针对于衍射误差的分析没有系统的理论或仿真模拟.在此基础上,本文通过仿真模拟,定量研究光栅衍射中衍射调节作用与菲涅尔衍射中半波带复振幅变化,从而可以定量探究近似条件应用范围,可以在工程光学中得到有效应用.

(1)

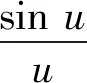
1 光栅衍射中定量研究衍射调节作用

1.1 设置缝宽a=30λ、3λ、1.22λ、λ,在10 mm的尺度下进行观测模拟

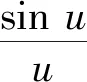
(2)

而双缝杨氏干涉强度分布为

I(θ)=4I0(cosβ)2,

(3)

缝宽依次设置为a=30λ、10λ、λ、0.1λ、0.01λ…

图1 观测尺度为10 mm,光栅衍射缝宽为30λ的衍射图样Fig.1 A diffraction pattern with an observation scale of 10 mm and a grating diffraction slit width of 30λ

图2 观测尺度为10 mm,光栅衍射缝宽为3λ的衍射图样Fig.2 A diffraction pattern with an observation scale of 10 mm and a grating diffraction slit width of 3λ

根据仿真模拟实验结果,在10 mm的观测尺度下,当光栅衍射缝宽a远大于λ时,衍射调节作用很强,图像主要呈现衍射图像,当a逐渐减小,接近λ时，衍射调节作用逐渐减小,图像逐渐变为干涉等光强图像.

1.2 设置a=0.1λ、0.01λ,在100 mm的尺度下进行观测模拟

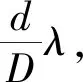
1.3 设置N=2,在尺度为1 mm时进行观测模拟

由图7～12可知，当a=15λ时，其光强明显受到衍射影响，但当a减少至a=10λ时，其光强便不再随着a的减小而发生明显改变，因此在双缝小尺度的观测情况下,可以将a=10λ当作衍射近似等同于干涉的极限点,此时衍射因子的作用可以忽略,强度分布可以当作干涉来处理.

图4 观测尺度为10 mm,光栅衍射缝宽为λ的衍射图样Fig.4 A diffraction pattern with an observation scale of 10 mm and a grating diffraction slit width of λ

图5 观测尺度为100 mm，光栅衍射缝宽为0.1λ的衍射图样Fig.5 A diffraction pattern with an observation scale of 100 mm and a grating diffraction slit width of 0.1λ

图6 观测尺度为100 mm，光栅衍射缝宽为0.01λ的衍射图样Fig.6 A diffraction pattern with an observation scale of 100 mm and a grating diffraction slit width of 0.01λ

图7 观测尺度为1 mm，光栅衍射缝宽为20λ的衍射图样Fig.7 A diffraction pattern with an observation scale of 1 mm and a grating diffraction slit width of 20λ

图8 观测尺度为1 mm，光栅衍射缝宽为15的衍射图样Fig.8 A diffraction pattern with an observation scale of 1 mm and a grating diffraction slit width of 15λ

图9 观测尺度为1 mm，光栅衍射缝宽为10λ的衍射图样Fig.9 A diffraction pattern with an observation scale of 1 mm and a grating diffraction slit width of 10λ

图10 观测尺度为1 mm，光栅衍射缝宽为5λ的衍射图样Fig.10 A diffraction pattern with an observation scale of 1 mm and a grating diffraction slit width of 5λ

图11 观测尺度为1 mm，光栅衍射缝宽为λ的衍射图样Fig.11 A diffraction pattern with an observation scale of 1 mm and a grating diffraction slit width of λ

图12 观测尺度为1 mm，光栅衍射缝宽为0.1λ的衍射图样Fig.12 A diffraction pattern with an observation scale of 1 mm and a grating diffraction slit width of 0.1λ

1.4 设置N=2,在尺度为100 mm时进行观测模拟

如图13～16，综合1.2～1.4的模拟结果可以初步得到观测尺度x,缝宽a及所用光波长λ在衍射可以看作干涉的条件下所近似满足的关系式如下：

(4)

图13 观测尺度为100 mm，光栅衍射缝宽为λ的衍射图样Fig.13 A diffraction pattern with an observation scale of 100 mm and a grating diffraction slit width of λ

图14 观测尺度为100 mm，光栅衍射缝宽为0.5λ的衍射图样Fig.14 A diffraction pattern with an observation scale of 100 mm and a grating diffraction slit width of 0.5λ

图15 观测尺度为100 mm，光栅衍射缝宽为0.4λ的衍射图样Fig.15 A diffraction pattern with an observation scale of 100 mm and a grating diffraction slit width of 0.4λ

图16 观测尺度为100 mm，光栅衍射缝宽为0.3λ的衍射图样Fig.16 A diffraction pattern with an observation scale of 100 mm and a grating diffraction slit width of 0.3λ

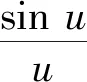
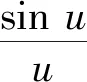
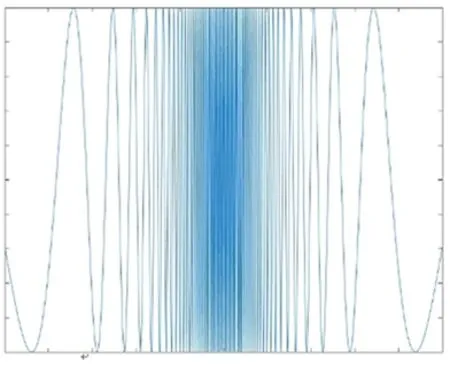
图17 光强分布曲线Fig.17 Light intensity distribution curve

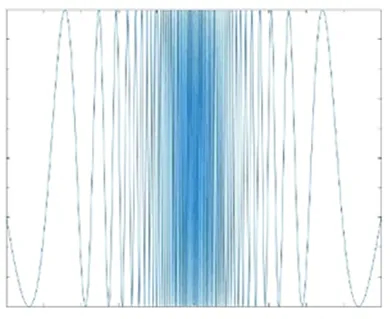
图18 当缝宽为0.1λ时的光强分布Fig.18 Intensity distribution when slit width is 0.1λ

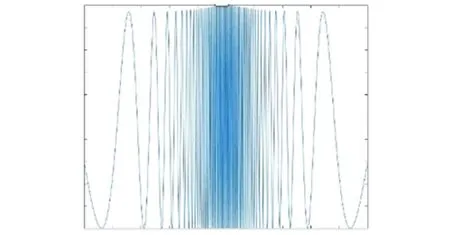
图19 当缝宽为0.01λ时光强分布Fig.19 Intensity distribution when slit width is 0.01λ

2 菲涅尔圆孔衍射中定量研究半波带复振幅变化

在圆孔衍射中,在球面上划分出的环带称为菲涅尔半波带.根据课本理论推理[1-3],复振幅

(5)

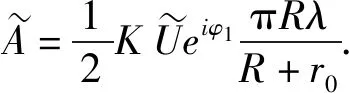
(6)

为第m个半波带发出的次波在P点的复振幅,其振幅大小为

(7)

其中相位(-1)m-1eiφ1,根据倾斜因子是连续缓慢变化的,所以可认为某1个半波带的振幅是与其相邻半波带振幅的平均值,故

(8)

由于相邻半波带振幅接近,所以相邻半波带间往往振幅大小可以接近,但相差很多时却不能简单地忽略不计.因此通过计算Am/A1,定量的计算当半波带数量n到多少时,振幅间的差距不可忽略.

由

(9)

可知

图20 菲涅尔衍射～m关系Fig.20 Fresnel diffraction ～m diagram

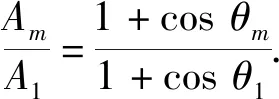
(10)

又因为

(11)

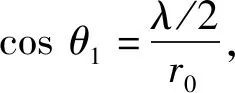
设定参数：r0=0.1 m，λ=800 nm. 代入数据模拟结果如图20.

由图20可知,在该参数下，当m=27 000时,Am/A1为95%,即出现了5%的误差，设该误差为所允许的极限误差,可以表明在该参数下m>27 000时,Am不能再约等于A1.

理论公式推导如下：

(12)

根据实际情况考虑,r0≫λ,可以化简为

(13)

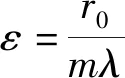
(14)

(15)

故当r0增大时,半波带振幅误差减小,当mλ增大时,半波带振幅误差增大.

3 结论

根据研究结论，可以在工程光学中对于现实问题采取适当的近似，将复杂的实际问题简易化。例如在光栅和波带片中便可根据样品参数不同采取不同程度的近似，从而得出较为便于应用的结果.