行星齿轮传动系统的降噪研究及参数优化

刘永平，魏凌强，魏永峭，李自军

（1.兰州理工大学机电工程学院，甘肃 兰州 730050；2.浙江午马减速机有限公司设计部，浙江 温州 325019）

1 引言

行星轮系是一种重要的齿轮传动机构，具有结构紧凑、体积小、质量轻、承载能力强及传递功率范围大等优点，已广泛应用于机械制造、航空航天、汽车船舶、工程机械等各个行业［1］。但是行星轮系的设计是一个复杂的问题，其计算参数多、计算过程繁琐，可能因为计算次数有限而漏掉最优解，且依照齿轮设计手册也容易忽略掉一些设计基准和要求，使整个行星轮系传动很难达到预期的各种性能指标，导致传动过程中出现振动和噪声问题［2-4］。

已知某型号的行星减速机具体参数，通过计算分析，发现该型号减速机不满足行星减速机设计要求的基本约束条件之中的约束条件，各啮合齿数之间有公约数且太阳轮齿数是行星轮数目的整数倍，这势必对整个轮系运行的平稳性产生影响，导致产生一定程度的噪声问题。针对上述问题，这里利用Kisssoft软件，仿真分析齿数关系对传动性能的影响，以及相同参数下，分析不同部件作为输入端时对传动系统性能的影响。以传动误差、齿面载荷分布以及接触斑点的优劣作为判断行星轮系传动精度高低的依据，得出最优的设计参数，为渐开线行星齿轮减速机的设计提供了一定的理论方法和依据。

2 行星轮系设计参数分析

2.1 行星轮系参数基本约束条件

行星传动各齿数不能随意选取，必须依据行星传动的特点，满足邻接条件、同心条件及装配条件等基本约束条件，才能进行正常传动［5］。

（1）邻接条件

邻接条件要求相邻两个行星齿轮不互相碰撞，可用下式表示：

（2）同心条件

为保证中心轮和行星架轴线重合条件下的正确啮合，由中心轮和行星轮组成的各啮合副的实际中心距必须相等，即为同心条件，可用下式表示：

（3）装配条件

装配条件要求n个行星轮能均匀装入轮系中，并且和太阳轮正确啮合而没有错位，可用下式表示：

式中：z1、z2、z3—太阳轮、行星轮和内齿圈的齿数；np—行星轮的数目；d12—行星轮齿顶圆的直径；cosα12、cosα23—太阳轮和行星轮、行星轮和内齿圈的实际啮合角。

2.2 主要性能指标

（1）传递误差

传递误差是指刚性条件下从动轮的实际占有位置与理想位置的差异，如图1所示。图中：A—主动轮齿廓；B—从动轮齿廓；B′—形变后从动轮齿廓。工作载荷下的齿轮的动态特性主要是由传递误差曲线的波动幅值来决定的，波动幅值愈大，振动愈大，即传递误差的幅值是振动的直接激励［6］。当内齿圈固定，太阳轮作为输入端，行星架作为输出端时，行星轮系的传递误差TE可用下式表示：

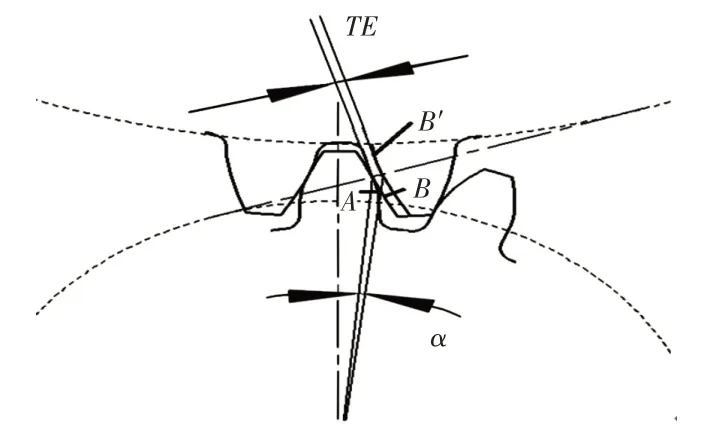
图1 传递误差图Fig.1 Transmission Error

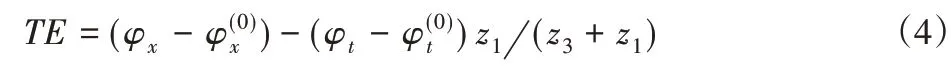
式中：φx、φt—行星架和太阳轮的转角；

行星架和太阳轮的初始转角。

对于行星轮系传递误差TE的计算主要基于齿轮制造误差TE（1由齿轮精度的单项误差构成，例如齿距累计偏差fp、齿廓偏差fα等）和齿轮接触变形TE2构成，其表达式如下：

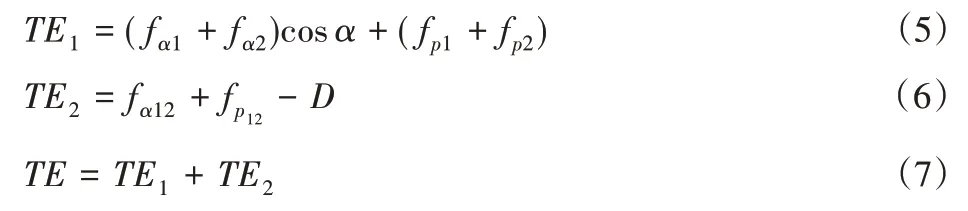
式中：D—轮齿接触变形量。

（2）啮合刚度

如果将齿轮传动的啮合过程近似看做一个弹性变化的过程，则齿轮得接触刚度是随着齿轮转动而不断发生变化的，这将导致轮齿间的啮合冲击，进而引起系统动态响应的变化，使系统产生振动和噪声。为了从本质上减小齿轮噪声，应使轮齿副传动过程中的刚度变化尽量柔和。一般来说，齿轮法向啮合刚度可用下式表示［6-9］：

法向啮合刚度和切向啮合刚度之间的关系为：

式中：T—齿轮的负载扭矩；

Δθ—齿轮的转角；

Fn—齿轮啮合点的法向力；

rb—齿轮的基圆半径；

δ—齿轮副沿啮合线方向的线性变形。

这里根据Weber-Banaschek法和Hook公式，将齿轮的综合弹性变形分为齿轮本身的变形、齿轮齿根处弹性变形、局部接触变形和赫兹变形。一般，啮合力的作用下，齿轮的变形主要由弯曲、剪切和压缩变形组成，利用悬臂梁模型来模拟齿轮的变形，如图3所示，这里采用能量法求得齿轮的弯曲刚度Kb、剪切刚度Ks和齿根压缩引起的刚度Kɑ，可以分别利用式（10）～式（12）计算得到。另外，在计算轮齿变形时应考虑齿轮的赫兹变形，如图4所示。即在计算系统啮合刚度时需要加上赫兹接触刚度Kh，可用式（13）计算得到。

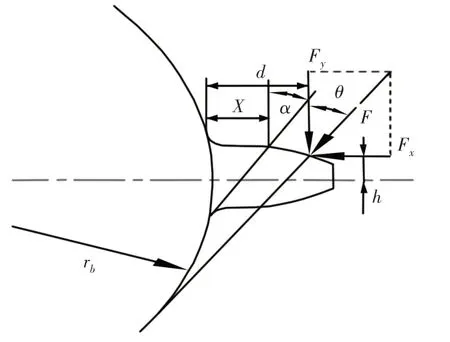
图2 轮齿啮合悬臂梁模型Fig.2 Gear Meshing Cantilever Beam Model

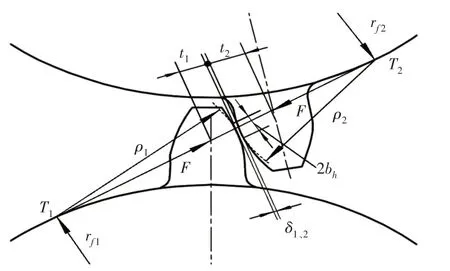
图3 赫兹刚度Fig.3 Hertz Stiffness

图4 行星轮系三维模型Fig.4 Three-Dimensional Model of Planetary Gear Train

式中：F—齿轮齿面载荷；

E和G—齿轮的弹性模量和剪切模量；

Ix、Ax—距离齿轮固定端X处截面的惯性矩和截面面积；

θ—齿轮副的啮合压力角。

综合可得，太阳轮和行星轮一对轮齿的总啮合刚度为：

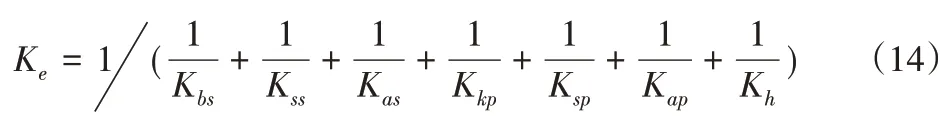
式中：下标s—太阳轮；下标p—行星轮。

3 行星轮系设计参数优化

根据该渐开线行星齿轮减速机相关型号与参数，如表1所示。利用Solidworks软件建立精确的三维模型，如图1所示，该轮系以太阳轮作为输入，行星架为输出，额定输出力矩为330Nm，额定输入转速为3000rpm。

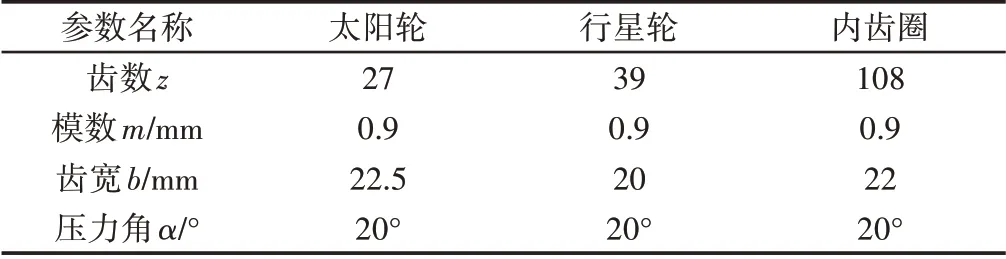
表1 原齿轮基本参数表Tab.1 Original Gear Basic Parameters

上述条件为行星齿轮减速机设计的基本条件，为了减少轮系传动的振动和噪声，提高其传动平稳性，在啮合的各齿轮副之间应最好没有公约数，且太阳轮的齿数也不宜为行星轮数目的整数倍。这里利用Kisssoft软件对这两个要求进行研究，分析不同形式下对行星轮系传动性能的影响大小，得出最佳的配齿方式。

在工况条件及模数、齿宽、压力角等齿轮基本原参数不变的条件下，只改变齿数，在Kisssoft软件中精筛选，可得到78组数据，如图5所示。

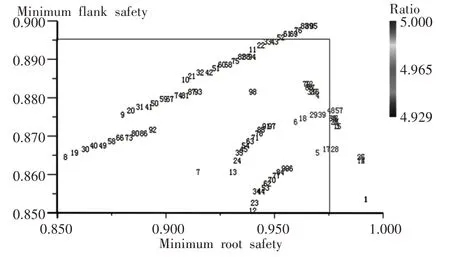
图5 齿轮齿数方案分布图Fig.5 Gear Tooth Number Scheme Distribution

依据齿轮最小弯曲疲劳强度和最小接触疲劳强度、各啮合齿轮副之间的齿数有无公约数和太阳轮的齿数是否为行星轮数目的整数倍，筛选出六组数据，如表2所示。

表2 齿轮齿数方案表Tab.2 Gear Tooth Number Scheme

对原齿轮齿数及筛选获得的六组齿数方案在Kisssoft软件中，进行具体的仿真分析。为了清晰了解不同齿数方案对传递误差、最大法向刚度、最大切向刚度以及最大应力的影响，将计算数据进行了图形化比较，具体如图6～图9所示。

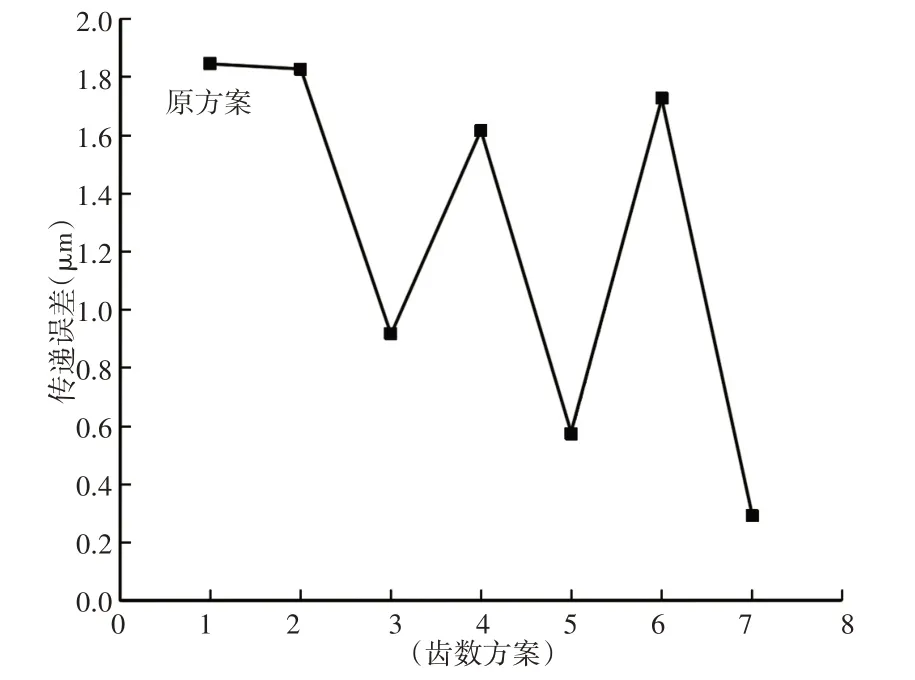
图6 传递误差对比图Fig.6 Transmission Error Comparison

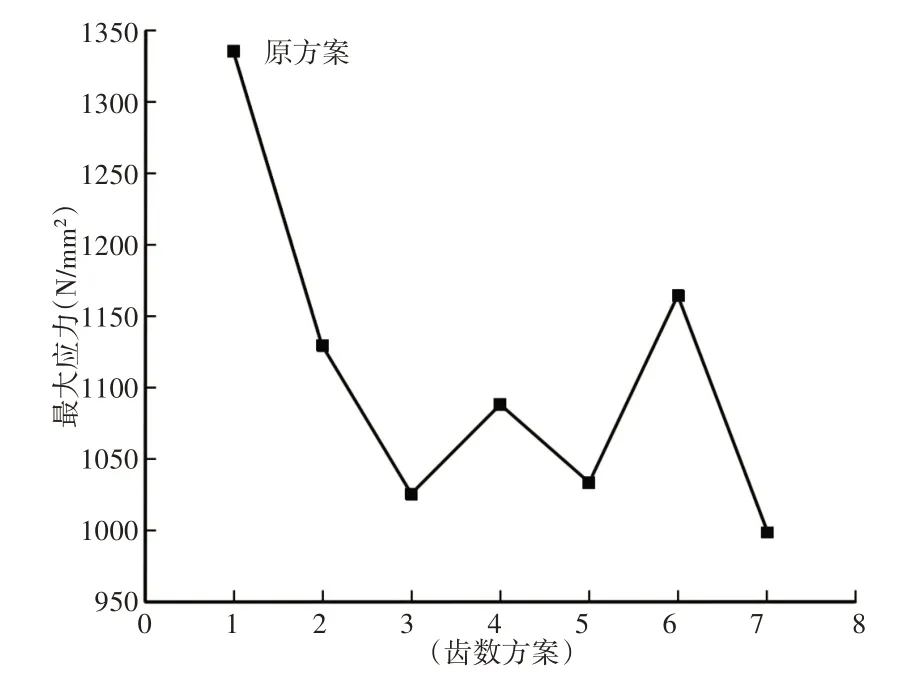
图9 最大应力对比图Fig.9 Maximum Stress Comparison

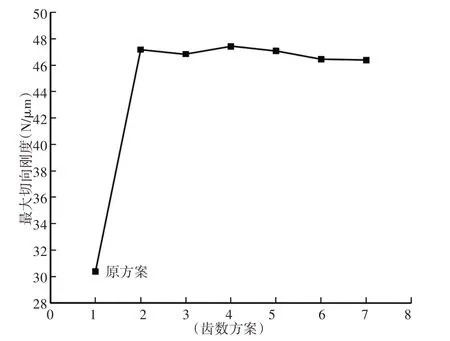
图8 最大切向刚度对比图Fig.8 Maximum Tangential Stiffness Comparison

图7～图10中，横坐标（1～7）分别代表不同的齿数方案，1为原齿数方案、（2～7）分别为表2中第一组到第六组齿数方案。

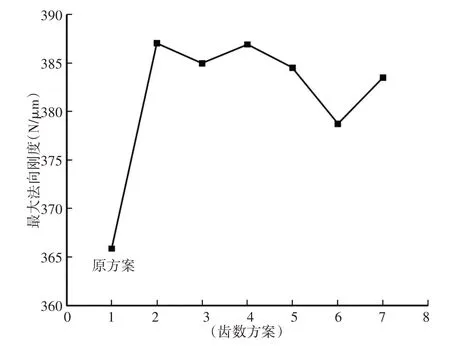
图7 最大法向刚度对比图Fig.7 Maximum Normal Stiffness Comparison

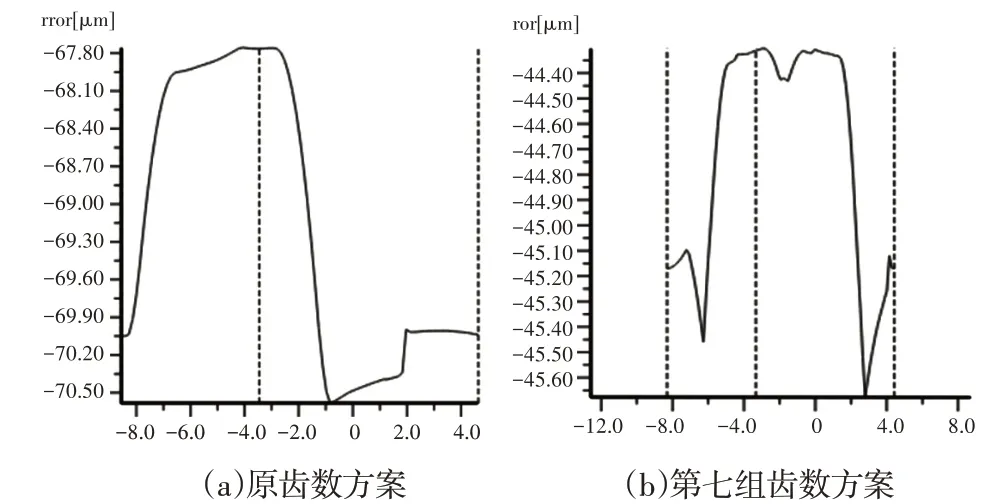
图10 传递误差曲线图Fig.10 Transfer Error Curve

通过对上面图表分析，虽然原方案的最大法向刚度和最大切向刚度相比其它六组方案略低，但综合比较下来，第七组齿数方案的行星轮系各项指标最优，即当行星轮系中太阳轮齿数不能整除行星轮数目，且太阳轮和行星轮、行星轮和内齿圈齿数互质时，其传递误差值和最大应力值均比其它齿数方案小。

为使计算结果更加直观，对第七组齿轮方案和原齿数方案进行TCA轮齿接触分析，如图11～图13所示。通过对比发现，传递误差由原齿数方案的1.847μm减小至0.292μm，降低了84.2%；且可明显发现原齿数方案的齿面载荷沿齿宽方向分布不均，存在一定的偏载现象，最大载荷为1335.547N/mm2，该齿数方案齿面载荷沿齿宽方向分布均匀、基本不存在偏载现象，最大载荷为998.281N/mm2，降低了25.3%。

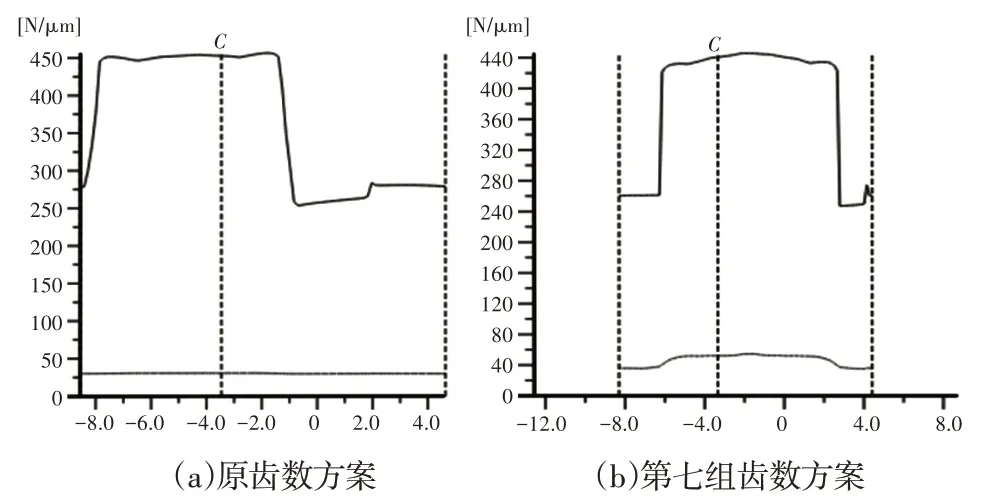
图11 刚度曲线图Fig.11 Stiffness Curve

图12 齿面接触载荷及分布图Fig.12 Tooth Surface Contact Load and Distribution Diagram

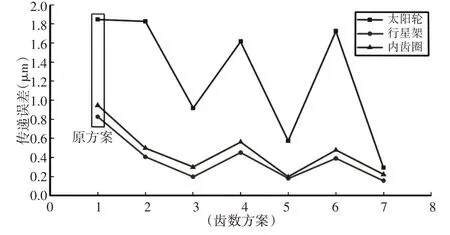
图13 传递误差对比图Fig.13 Transmission Error Comparison

4 行星轮系输入端仿真分析

目前，齿轮传动系统的动态激励分为外部和内部两种激励。其中，外部激励是指激励由外部施加给传动系统的，大部分由原动机的主力矩引起。反之，由传动系统内部产生的激励称为内部激励。大多数研究旨在通过改变轮系结构参数或者轮齿修形来改善轮系内部激励，达到减振、降噪的目的，而忽视了改善外部激励［10-12］。

行星轮系的输入端可以为太阳轮、行星架及内齿圈，本节在不改变轮系结构参数和激励特性的情况下，通过改变行星轮系的激励位置，研究分析轮系的动态特性，实现减振、降噪的目的。

对原齿数方案及上述得到的六组齿数方案进行仿真分析，将不同齿数方案得到的传递误差、最大法向刚度、最大切向刚度以及最大应力的将数据进行图形化比较，具体如图14～图17所示。

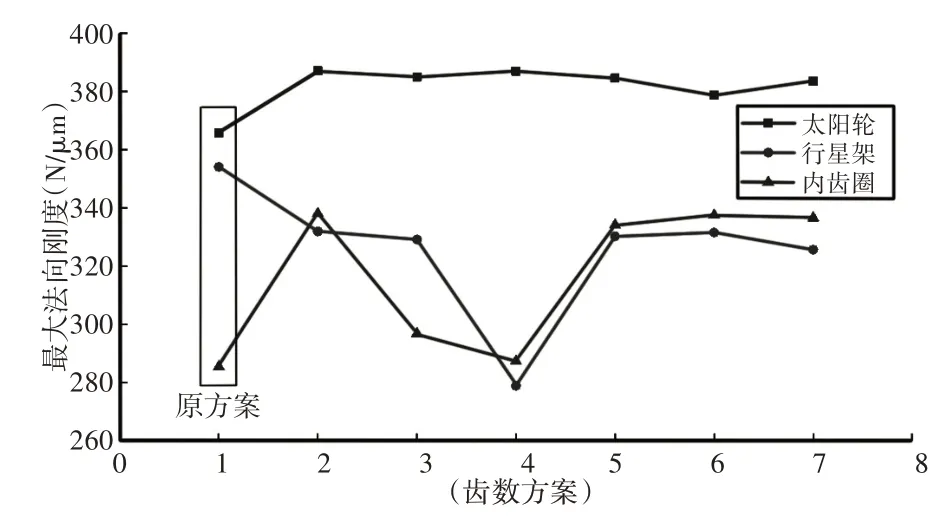
图14 最大法向刚度对比图Fig.14 Maximum Normal Stiffness Comparison

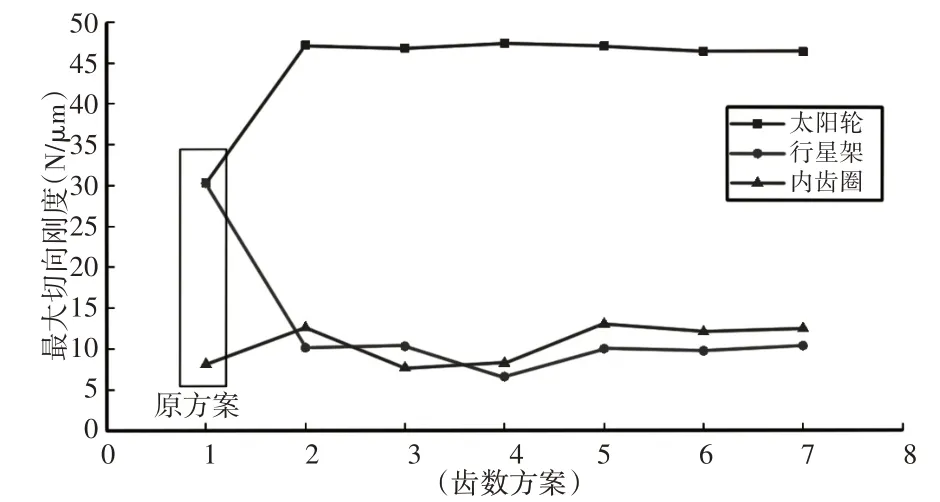
图15 最大切向刚度对比图Fig.15 Maximum Tangential Stiffness Comparison

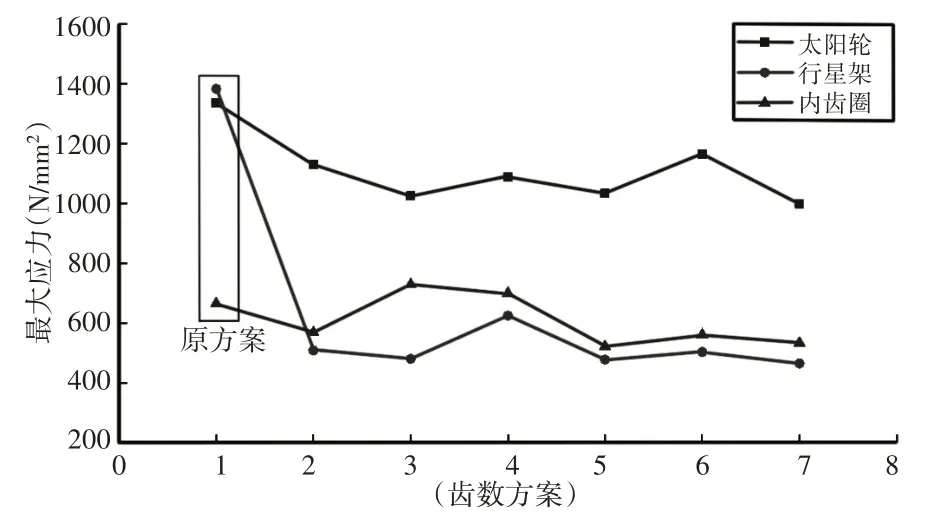
图16 最大应力对比图Fig.16 Maximum Stress Comparison

图14-图17中，横坐标1-7分别代表不同的齿数方案，1为原齿数方案、2-7分别为表2中第一组到第六组齿数方案。

图17 某型号行星减速机实体Fig.17 Planetary Reducer Entity of a Certain Type

通过对上面图表分析，可以得出当行星轮系把行星架作为输入端时，其工作状态要比把太阳轮或内齿圈作为输入端时优良。以第七组齿数方案为例，当行星架作为输入端时，相比太阳轮作为输入端，传递误差由0.292μm减小至0.157μm，降低了46.2%；太阳轮作为输入端时法向刚度为383.4678N/μm，切向刚度为46.3794N/μm，当行星架作为输入端时法向刚度降为325.6931N/μm，切向刚度降为10.4201N/μm，分别降低了15%和77.5%；太阳轮为输入端时齿面最大载荷为998.281N/mm2，行星架作为输入端时齿面最大载荷为464.438N/mm2，降低了53.5%。另外，通过TCA齿面接触分析可得出，当行星轮系以行星架作为输入端时，其齿轮弯曲强度和接触强度要优于于太阳轮和内齿圈作为输入端时的强度。

最后，基于已得到的理论仿真结果，以第七组最优参数作为方案，加工出一台减速机实体，如图18所示。并在齿轮箱检测仪中进行试验，如图19所示。结果表明，检测数据十分接近理论数据。通过实验验证，为该型号减速机的减振降噪提供了可行的依据。

图18 齿轮箱检测仪Fig.18 Gear Box Detector

5 结论

这里在Solidworks软件中建立了渐开线变位直齿轮行星轮系的精确模型，之后导入Kisssoft软件中进行TCA轮齿接触仿真分析。通过啮合的各对齿轮之间是否有公约数，太阳轮的齿数是否为行星轮数目的整数倍，及行星轮系不同输入端情况下的不同齿数方案的对比分析，这里得到以下结论：

（1）当啮合齿轮副的齿数之间存在互质关系时，齿面应力基本不存在偏载现象，且满足行星轮与内齿圈之间的互质是最重要的；

（2）当满足太阳轮齿数不为行星轮数目的整数倍时，行星轮系的传递误差、啮合刚度及齿面接触应力比可以整除的要好；

（3）渐开线行星轮齿轮减速机由行星架作为输入端时，其工作性能比太阳轮和内齿圈作为输入端时要优良。