考虑偏载的行星轮系功率流及传动效率计算
2022-10-11李园园王迎波高文进
李园园 王迎波 高文进 任 伟
(潍柴动力股份有限公司新能源研究院,山东潍坊 261061)
行星轮系因具有传动比大和承载能力高等优点被广泛应用在机床等设备中。传动效率是评价行星轮系性能的一个重要指标。对于行星轮系的传动效率问题,国内外学者进行了大量的研究,取得了众多的成果。例如,王成[1]利用啮合功率法,推导出行星轮系传动效率的简化计算公式。Fanghella P[2]根据锥齿轮行星轮系的传动特点,提出锥齿轮行星轮系传动效率的计算式。Chen C[3]首次提出了虚功率和虚功率比的理论,并将它们应用到行星轮系传动效率的研究中。Wang C[4]根据虚功率和虚功率比理论,提出了行星轮系传动效率的计算方法。胡青春等[5]应用虚功率理论,对带有圆锥齿轮的复合行星轮系传动功率流与传动效率进行了分析。
为了提高行星轮系的刚度和承载能力,通常采用多个行星轮均布在中心轮四周的结构(如图1a所示)。然而,目前对于行星轮系传动效率的研究,通常考虑的是行星轮系传动的理想状态,即均载。这样,在分析行星轮系中齿轮啮合的时候,仅考虑了一个行星齿轮,如图1b所示。但由于安装和加工误差的存在,行星轮系在传动过程中会出现偏载现象,这样再采用理想方法来分析行星轮系的传动效率是不精确的。
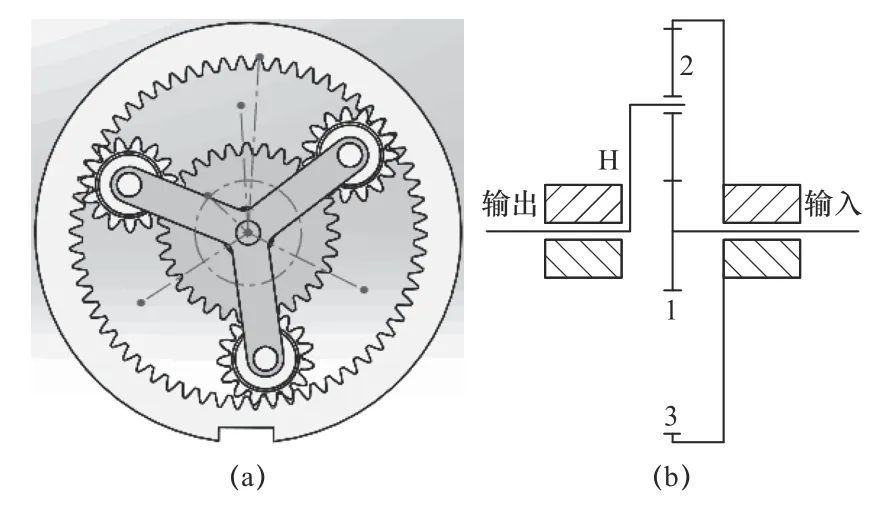
图1 行星轮系
基于此,以实际应用最多的2K-H型行星轮系为研究对象,提出了一种适用于多工况下行星轮系功率流及传动效率的计算方法。
1 行星轮系传动效率计算
1.1 考虑偏载的行星轮系和转化轮系功率流图绘制
根据图论相关理论,考虑偏载的影响,绘制行星轮系和转化轮系功率流图,绘制的原则包括:(1)考虑行星轮系中全部行星轮的功率流。(2)轮系中的构件包括全部行星轮分别用①、㉑、㉒、㉓、③和Ⓗ表示。(3)只考虑齿轮副的功率损失,忽略构件组成的其他运动副的功率损失。因此,机架和与机架通过运动副连接的构件之间的功率流为0。(4)为了简化起见,图中的齿轮副没有绘出。根据上述原则,行星轮系和转化轮系中功率流分别如图2和图3所示。其中,行星轮系中中心轮3为机架,功率由中心轮1输入,行星架H输出;转化轮系中行星架H为机架,功率由中心轮1输入,中心轮3输出。

图2 行星轮系功率流图
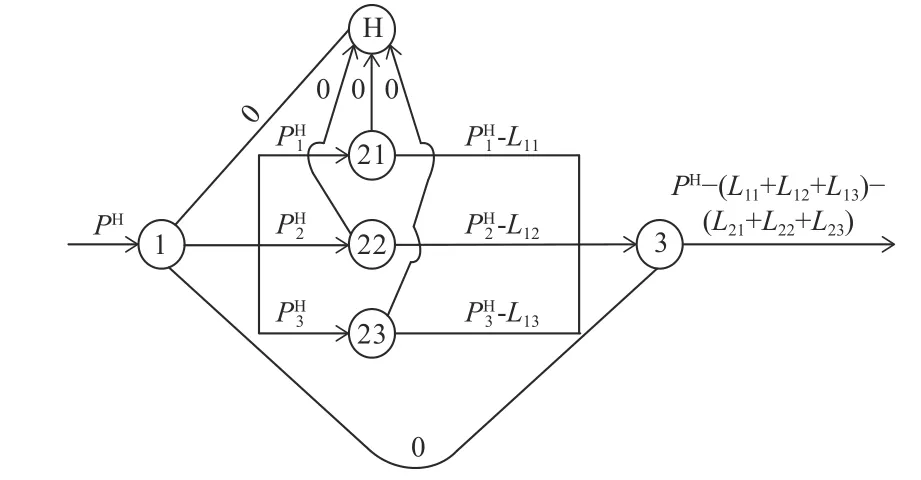
图3 转化轮系功率流图
若不考虑偏载的影响,即均载工况,可以将图2和图3进行简化,即将所有的功率都施加在一个行星轮上,均载工况下行星轮系和转化轮系功率流图分别如图4和图5所示。

图4 均载工况下行星轮系功率流图
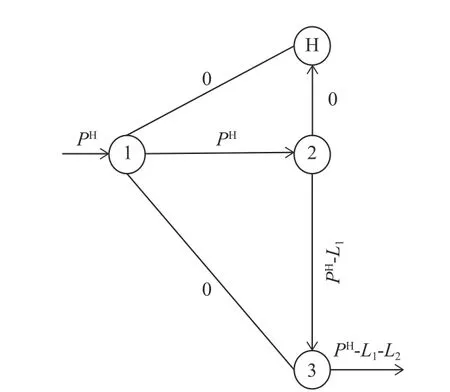
图5 均载工况下转化轮系功率流图
对比图2~5可以发现:(1)当流经各行星轮的功率相等时,即均载,图2~5对于功率流的表示方法本质上是相同的。(2)当流经各行星轮的功率不相等时,即偏载,图2、图3能详细地描述各行星轮的功率流向。综上所述,图2、图3既可以描述均载工况下的功率流向,也可以描述偏载工况下的功率流向,因此适用于多工况下行星轮系功率流及传动效率的计算。
1.2 行星轮系传动效率计算
应用虚功率理论对行星轮系的传动效率进行计算。虚功率理论的核心思想是:构件所受的力矩与机架的选取无关。对于行星轮系和转化轮系而言,其作为机架的构件发生了改变,但构件所受的力矩不变。因此,基于虚功率理论,可以算出流经构件的功率,具体计算如下


功率流经行星轮1时(功率流图中的㉑),根据虚功率理论可得

功率流经行星轮2时(功率流图中的㉒),根据虚功率理论可得

功率流经行星轮3时(功率流图中的㉓),根据虚功率理论可得
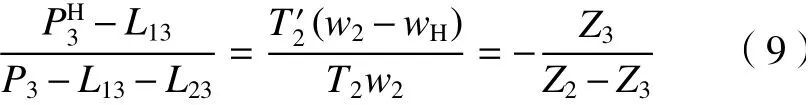
根据虚功率理论,式(7)~(9)中行星轮系和转化轮系中相应构件所受的扭矩相等。
行星轮系传动效率计算公式可表示为

联立式(1)~(10),可以得到行星轮系的传动效率η。
1.3 偏载对行星轮系传动效率的影响
这里,以图1行星轮系为例,对均载和偏载工况下行星轮系的传动效率进行比较。需要指出的是,齿轮副的传动效率与所受载荷有关,当载荷发生变化时,齿轮副的传动效率相应发生变化。
(1)均载工况
对于这种情况,流经3个行星轮的功率相等且3个行星轮与两中心轮分别啮合时的传动效率相等,即
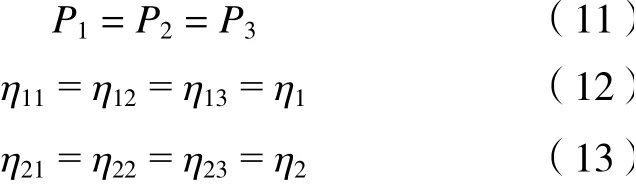
将式(11)~(13)代入式(1)~(10)中,可以得到均载工况下行星轮系的传动效率。
(2)偏载工况
对于这种情况,流经3个行星轮的功率不相等且3个行星轮与两中心轮分别啮合时的传动效率不相等,即


将式(14)~(16)代入式(1)~(10)中,可以得到偏载工况下行星轮系的传动效率。
与式(11)~(13)相比,式(14)~(16)中行星齿轮的传动功率和传动效率均不相等,因此,均载工况和偏载工况下行星轮系的传动效率将会存在差异。因为式中涉及的参数众多,具体比较结果我们将会在后面具体实例中计算得出并讨论。
2 应用算例
以某单级NGW减速器为例(图6),对其传动效率进行计算,该行星轮系的主要参数如表1所示。

图6 单级NGW减速器

表1 行星轮系参数
2.1 行星轮系传动效率计算
(1)计算行星轮齿数z2和中心轮齿数z3
根据行星轮系的同心条件,可得
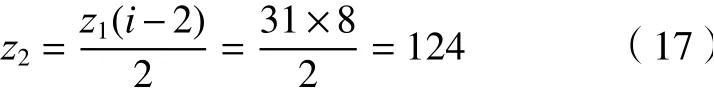
根据行星轮系的传动比条件,可得

(2)计算行星轮系传动效率
分别计算均载工况和偏载工况下行星轮系的传动效率,然后进行比较。
①均载工况
流经3个行星轮的功率相等,即各为P/3,假定行星轮与两中心轮分别啮合时的啮合效率η1=0.94和η2=0.96。
将上述已知量代入式(1)~(10)中,可得

②偏载工况
这里假定P1=3.5 kW,P2=3.3 kW,P3=3.2 kW,它们的和等于输入功率P。上文已经指出,齿轮副的传动效率与所受载荷有关,当载荷发生变化时,齿轮副的传动效率相应发生变化。因此,假定行星轮与两中心轮分别啮合时的传动效率η11=0.945,η12=0.94,η13=0.92,η21=0.965,η22=0.96,η23=0.94。与均载工况下的齿轮副传动效率存在差异。
将上述已知量代入式(1)~(10)中,可得

对比第一种情况和第二种情况,二者差值为0.014 8。因此,当存在偏载工况时仍采用均载工况下的计算公式将影响轮系传动效率计算的精确性。
2.2 行星轮系传动效率模型验证
为了验证所推导行星轮系传动效率计算公式的准确性,我们借助于行星轮系动力学模型的分析结果,对行星轮系传动效率的计算结果进行验证。
首先在Creo软件中建立行星轮系的三维模型。然后,将三维模型导入到ADAMS软件中,根据行星轮系的运动方式,添加所有构件的配合关系,包括中心轮,3个行星轮,内齿圈以及行星架的配合关系。利用Hertz接触理论,根据行星轮系的力学传递关系,给齿轮之间的啮合添加IMAPACT接触力,包括啮合力指数、穿透深度、刚度系数、阻尼系数、静摩擦系数和动摩擦系数(行星轮系动力学模型如图7所示)。设置电机输入驱动和输入转矩,设定仿真实验时间和步长,采用SI2积分器求解得到构件的动力学参数,得到动态输出扭矩和动态输出转速(图8),与输入扭矩和输入转速一起,计算得到行星轮系动态传动效率(图9),动态传动效率的平均值为0.852,其他值围绕平均值波动,与2.1节情况1中计算得到的传动效率相比,误差在2%以内,验证了行星轮系传动效率计算的可行性。由于动力学模型分析的局限性,对于偏载时传动效率的仿真计算,我们将会在以后的研究中进行分析。

图7 行星轮系动力学模型

图8 动态输出扭矩和动态输出转速
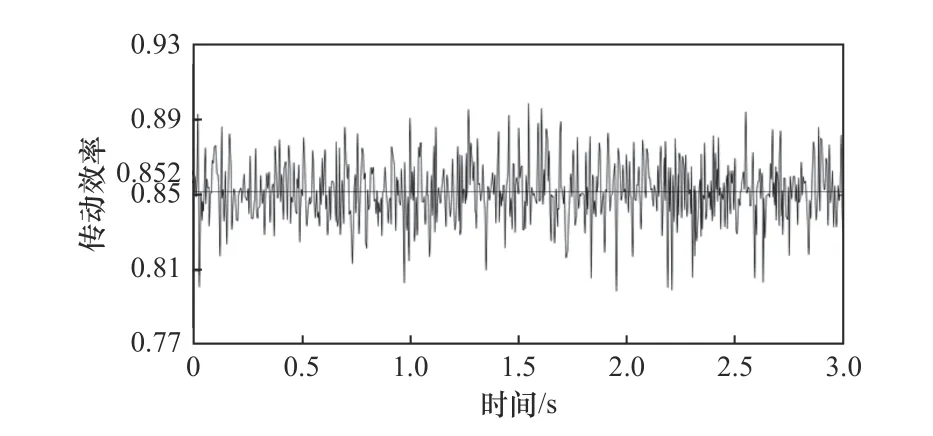
图9 行星轮系动态传动效率
3 结语
(1)考虑行星轮系传动过程中偏载等现象,利用虚功率理论,提出了一种适用于多工况下行星轮系功率流及传动效率的计算方法。
(2)以某单级NGW减速器为例,分均载和偏载两种情况对行星轮系的传动效率进行了计算。对比结果表明,二者差值较大。从而可以得出,当存在偏载工况时仍采用均载工况下的计算公式将影响轮系传动效率计算的精确性。
(3)借助于行星轮系动力学模型的分析结果,计算得到行星轮系的动态传动效率。其平均值与均载工况下计算得到的传动效率相比,误差在2%以内,验证了行星轮系传动效率计算模型的可用性。
(4)利用本文所提出的方法可以计算多种工况下行星轮系的传动效率。为下一步行星轮系的传动性能改善提供了理论指导。
