基于LPFSA与阶次跟踪的变速齿轮箱状态评估
2022-02-23唐敏
唐 敏
(大连职业技术学院电气电子工程学院,辽宁 大连 116037)
1 引言
行星齿轮箱以其结构紧凑、传动比高、承载能力大的独特特点被广泛地集成到各种旋转机械中[1,2]。由于工作环境恶劣,行星齿轮箱容易损坏,导致整个机械系统性能下降甚至停机。为了有效地提高机器运行的可靠性和降低维护成本,状态评估在现代工业中是必不可少的[3]。
对于行星齿轮箱的状态监测,编码器信号比传统振动信号有许多优点[4]。首先,编码器信号消除了时变传输路径引起的幅度调制现象。此外,编码器信号可以直接从内置的旋转编码器获取,而不必侵入行星齿轮箱。最后,编码器信号具有相对较高的信噪比。因此,基于编码器信号的状态评估方法在克服振动分析的缺点的同时,为行星齿轮箱的状态评估提供了另一个可行的解决方案[5]。
在文献[6]中,首先从编码器信号中测量轴的瞬时角速度,然后将其应用于叶片的健康评估。文献[7]研究了连接误差和量化误差对,用经过时间法从编码器信号中获得的速度信息精度的影响,并提出了编码器几何补偿算法,从而准确地从编码器信号中提取速度信息。此外,文献[8]提出了一种基于经验模态分解和自相关局部倒谱相结合的齿轮箱多级故障检测方法。文献[9]提出了利用梳状滤波、基尼引导的残差奇异值分解和迭代马氏距离识别行星齿轮箱的健康状况。尽管编码器信号分析取得了显著进展,但是现有的方法大多集中在恒定转速条件下的编码器信号分析,而对其时变故障特征的研究还不够深入,因此,基于编码器信号的变速箱故障检测仍然具有挑战性。
针对这一问题,提出了一种基于局部多项式拟合稀疏算法与阶次跟踪(LPFSA-OT)的变速齿轮箱编码器信号瞬态特征提取算法,用于识别变速箱在变速工况下的健康状况。最后通过仿真和实验验证了提出方法的有效性。
2 基本理论
2.1 局部多项式拟合
考虑噪声观测y的近似多项式信号p:

式中:p∈RN很好地近似于d次多项式,w∈RN—具有零均值的高斯白噪声;x(t)∈RN—故障引起的角瞬变。为了从噪音信号y中预估多项式信号p,提出了以下优化问题:
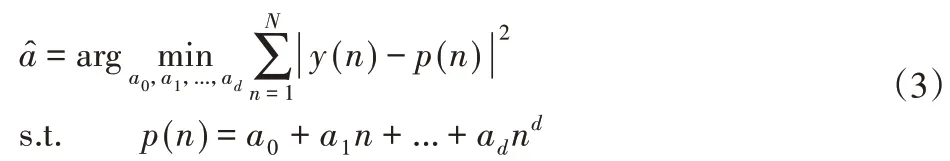
式中:N—信号长度,d次多项式满足d<<N。
为方便起见,将优化问题(3)转换为矩阵形式,可以表示为:

式中:G—大小为N×(d+1)的范德蒙德矩阵,多项式数ɑ为大小(d+1)×1的向量。

优化问题(4)是一个标准最小二乘问题,其解决方案可以被明确的表示为:

然后,多项式信号p由p^=Gɑ^=G(GTG)-1GTy给出。残差由给出,可以将其重写为其中H=I-G(GTG)-1GT。
然而,上述近似所有N-point数据内的多项式信号的多项式拟合通常适用于相对短的信号。因此,对于具有N-point数据的长信号,在M个局部块内执行多项式拟合是合理的,该M个局部块是通过在整个N-point数据上滑动长度为L的窗口而获得的。上面的方法是所谓的局部多项式拟合。请注意,上述参数满足,其中,P表示连续块的重叠长度,其范围设置为0≤P≤L-1;[X]表示将X舍入为小于或等于X的最接近整数的运算符。为了符号上的方便,引入大小为L×N的矩阵Sm,将N-point划分为M个段,每个段的P点重叠。相应地,矩阵表示将第m个块置于N-point数据中的第m位置的过程。对于范围1≤m≤M中的每个m,相应的局部块定义为ym=Smy。例如,当N=9,L=5且P=3时,矩阵S2可以表示为:

此外,值得注意的是,矩阵Sm和diɑg(sm),其中diɑg(s)返回一个平方对角矩阵,其中向量s的元素位于主对角线上。例如,对应于(7)中的矩阵S2的向量s2是s2=[0 0 1 1 1 1 1 0 0],在基本介绍了局部块和矩阵Sm之后,进一步给出了局部多项式拟合的数学表达式:
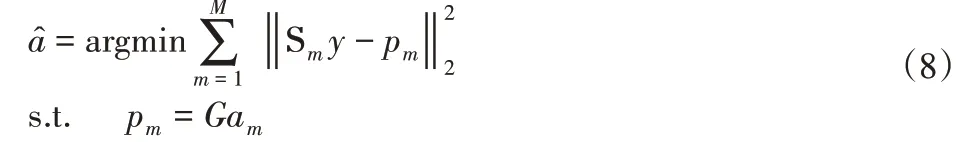
其中矩阵G的大小为L×(d+1)。相应地,第m块的多项式系数ɑm和残差wm分别为其中H=I-G(GTG)-1GT。
2.2 稀疏表示
稀疏表示已在图像处理和信号处理中受到广泛关注,其核心是在冗余字典上找到信号的最稀疏表示[10]。基于稀疏性算法的数学模型可以表示为:

式中:y∈RN—被测信号;D∈RN×M和x∈RM—冗余字典和稀疏系数。此外,稀疏正则化器R(x)用于提高系数x的稀疏性,而λ>0是保持数据保真度和稀疏性之间平衡的正则化参数。
为了获得令人满意的稀疏表示性能,必须针对特定问题仔细构建冗余字典D和稀疏正则化器R(x)。在文献[11]中,为了从噪声振动信号中提取出低振荡分量和高振荡分量,基于可变换的Q因子小波变换建立了超完备字典,并选择l1=norm作为正则化器。此外,引入了广义极大极小凹惩罚作为非凸正则化器,以提高l1=norm正则优化问题的性能。在文献[12]中,为了从测量的振动信号中提取出在时域中表现出组稀疏特性的故障瞬变,将重叠的组稀疏性合并到正则化器中,并将冗余字典D设置为单位矩阵I。优化极小化算法(majorization minimization,MM)算法是一种将复杂问题隐蔽为较简单问题的方法。考虑关于u的目标函数F最小化的凸优化问题:

可以通过迭代算法获得优化问题(10)的解:

式中:Q—目标函数F在(10)中的主化器,而i是迭代索引。
此外,主化器必须遵循约束:

在这里,给出了绝对函数||u的主化器,它将在以下算法推导中使用。
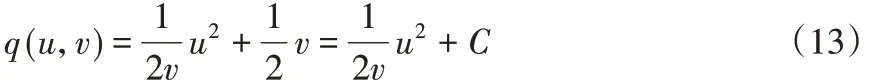
其中,C不依赖于u。
3 提出的瞬态特征提取算法
3.1 局部多项式拟合稀疏算法
从发生齿轮故障的行星齿轮箱获取的编码器信号通常是累积的角位置,谐波分量,故障引起的角瞬变和背景噪声的混合物,该信号记录受监控轴的角位置,并可以表示为:
公众保护意识不高、对相关法律的陌生是野生动物非法贸易高发的主要原因。在一些边远山区,野生动物的保护工作没有引起高度重视,一些短视行为使野生动物的栖息场所被破坏。野生动物的引种、驯养、繁殖等管理滞后,漏洞较多。加之,近年来,人们饲养的野生动物数量、种类越来越多,濒危等级越来越高,这引发了大量野生动物贸易问题。大量龟类、爬行类、鸟类,甚至威猛的老虎都成了人们饲养的宠物。炒作的价格、买卖利润高昂,刺激了野外偷猎和贸易。

式中:多项式分量p(t)∈RN—累积的角位置和谐波分量的混合,可以通过多项式很好地近似;x(t)∈RN和w(t)∈RN—故障引起的角瞬变和白高斯噪声。
此外,应该指出的是,故障瞬变表现出群体稀疏性,这意味着瞬态信号中的大幅度值不仅稀疏而且趋于形成群体。编码器信号的更多基本特性在第4节中进行了说明。
为了从原始编码器信号y(t)中提取时域瞬态特征x(t),提出了一种基于局部多项式拟合和稀疏性的算法,并且可以采用相应的优化问题表示为:
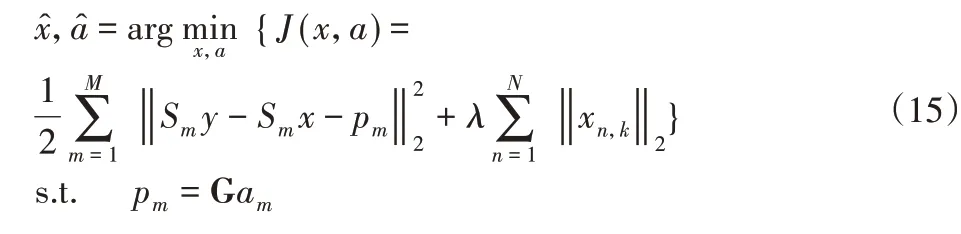
其中,多项式分量p(t)通过在L-point局部块pm内执行多项式逼近来表示。局部块的数量为M,多项式次数为d。另外,基于重叠群稀疏性构造正则化函数用来促进瞬态特征的群稀疏性,其中xn,K=[xn,xn+1,...,xn+K-1]∈RK,K表示组大小。
假设x是固定的,则仅针对多项式系数ɑm执行最小化。因此,优化问题(15)与应用于信号y-x的(8)相同,(15)关于系数的解为:

将式(16)代入式(15),最优化问题式(15)可以表示为:
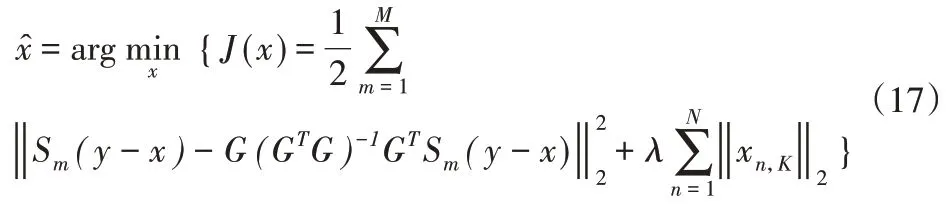
此外,通过H=I-G(GTG)-1GT,可以将优化问题式(17)进一步写为:
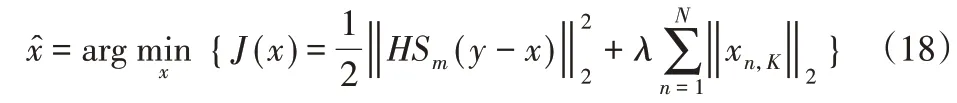
3.2 算法推导
在本节中,基于乘法器的交替方向方法和MM算法来推导迭代收敛算法,以解决优化问题式(18)。由于问题式(18)的严格凸性,经过多次迭代后即可轻松获得最佳解。
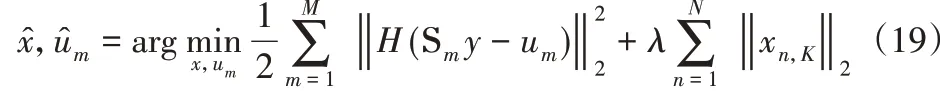
其受um=Smx,m=1,2,...,M的约束,在ADMM应用于约束优化问题(19)之后,得出以下迭代算法。
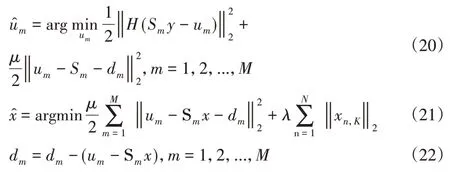
为了解决子问题式(20)和式(21),详细的推导过程描述如下:
优化问题式(20)是最小二乘问题,其解决方案可以明确表示为:
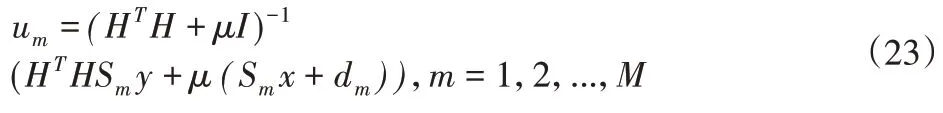
由于计算(23)的计算成本高,在将H=I-G(GTG)-1GT代入式(23)后使用矩阵逆引理[14],则上述表达式可进一步写为:
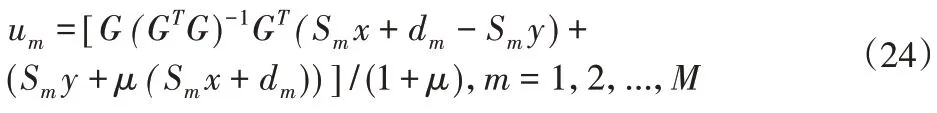
矩阵GTG的大小为(d+1)×(d+1),度d<<N,因此矩阵GTG和式(24)的求逆可以有效地求解。
为了使子问题式(21)中的目标函数:
F(x)=最 小 化,将F(x)定义为:
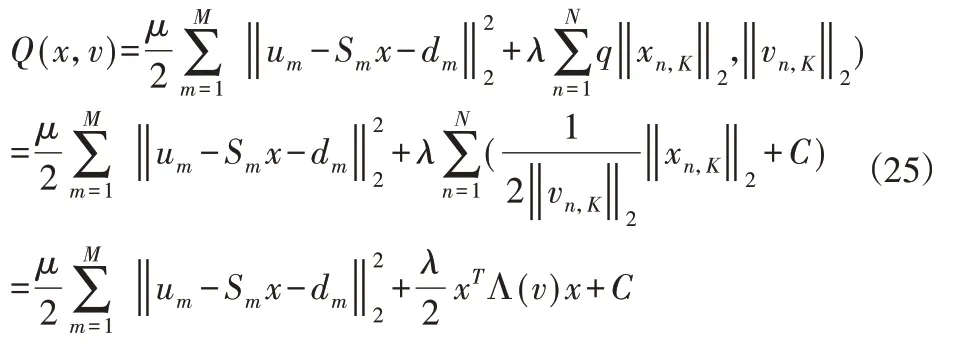
式中:Λ(v)—对角矩阵,其对阵元素为:

在MM算法更新迭代中使用式(25):

然后通过下式迭代获得最优解:
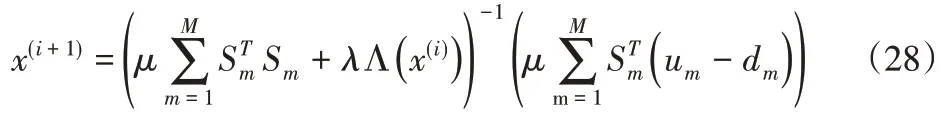
3.3 阶次跟踪技术
当行星齿轮箱在变速条件下运行时,通过局部多项式拟合稀疏算法提取的时域瞬态特征x(t)是非平稳的。因此,采用阶次跟踪技术以恒定的角度增量对时域瞬态特征x(t)进行重采样,这意味着将时域中的非平稳瞬态特征x(t)转换为如图1所示的一个角度中的平稳x(θ)领域。为了保证阶次跟踪的完美性能,准确获取瞬时相位是必不可少的。如上所述,原始编码器信号y(t)记录了旋转分量的角位置,因此可以将其用作相位参考信号进行信号重采样。与原始编码器信号y(t)相比,多项式信号p(t)作为相位参考信号是更好的选择,因为在多项式信号p(t)中有效地去除了干扰成分。因此,在所提出的方法中,将多项式信号p(t)选择为用于信号重采样的相位参考信号。
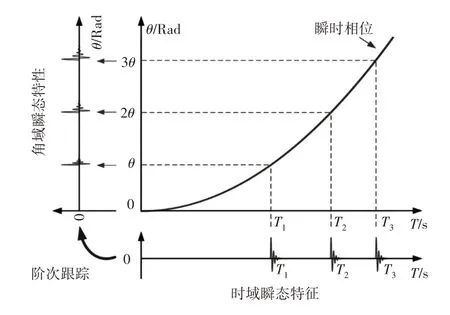
图1 阶次跟踪技术示意图Fig.1 Schematic Diagram of the First Order Tracking Technology
3.4 算法流程
瞬态特征是行星齿轮箱存在机械故障的重要指标,因此瞬态特征提取在状态评估过程中是必不可少的。在本节中,提出了一种新颖的瞬态特征提取算法,该算法可以有效地从变速条件下获取的噪声编码器信号中提取故障特征。在图2中详细说明了所提出的方法LPFSA-OT的过程。在所提出的方法中,通过局部多项式拟合稀疏算法提取了与行星齿轮箱健康状况相关的时域瞬态特征。之后,采用阶次跟踪将时域中的非平稳瞬态特征转换为角域中的平稳瞬态特征。最后,基于角域中的瞬态特征识别健康状况。

图2 提出的用于行星齿轮箱状态评估方法的流程图Fig.2 The Flow Chart of the Proposed State Evaluation Method for Planetary Gearbox
4 仿真分析
4.1 仿真模型
在变速条件下运行的故障行星齿轮箱的编码器信号是多个组件的组合,可以表示为:
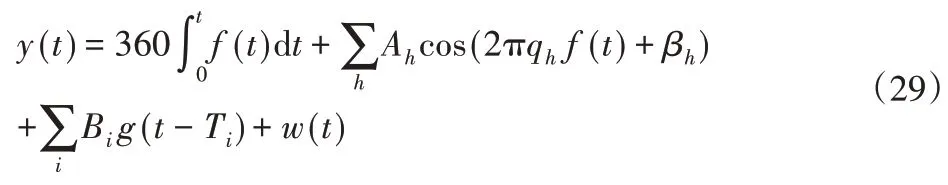
其中,

第一项是累积角位置,其中,f(t)代表瞬时旋转频率。第二项表示由负载变化或齿轮啮合引起的谐波分量,其中,A h和βh分别是第h次谐波的振幅和初始相位。qh是第h次谐波分量的谐波阶次,可以选择为整数和非整数。另外,第三项代表由齿轮故障引起的角瞬变,其中Bi和Ti是第i个瞬变的幅度和发生时间。采用余弦函数的一个后期来模拟角瞬变。最后,最后一项描述了由测量噪声和旋转编码器的制造误差引起的白高斯噪声,其中,w(t)~N(0,σ2)和σ表示标准推导。在此仿真中,假设行星齿轮箱在信号采集过程h中经历了加速和减速过程,并且速度曲线可以表示为:
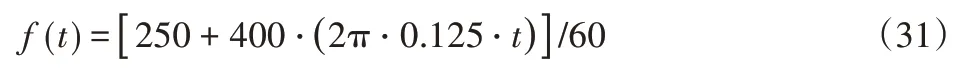
假设由负载变化和齿轮啮合引起的谐波分量同时包含在编码器信号中,并且振幅,初始相位和谐波阶数分别为A1=6.55,β1=π 4,q1=1,A2=0.23,β2=π 6,q2=20。此外,在仿真信号中将故障顺序设置为forder=2,这意味着角域故障瞬态的重复周期为360°/2=180°。可以根据转速曲线f(t)和故障阶跃forder确定相应的时间。此外,将故障瞬变的振幅Bi设置为0.44。
模拟编码器信号的采样频率和时间长度分别为5000Hz和4s。图3显示了速度曲线,从中可以看出行星变速箱经历了一个很大的速度变化。图4(a)显示了累积的角位置,其中曲线的斜率与编码器轴的瞬时转速成正比。此外,载荷变化和齿轮啮合引起的谐波分量分别显示在图4(b)和(c)中。图4(d)显示了与(29)中的第三项相对应的故障引起的角瞬变。累积角位置、由负载变化引起的谐波分量、齿轮啮合引起的谐波分量、角瞬变、高斯白噪声,如图4(a)~图4(e)所示。
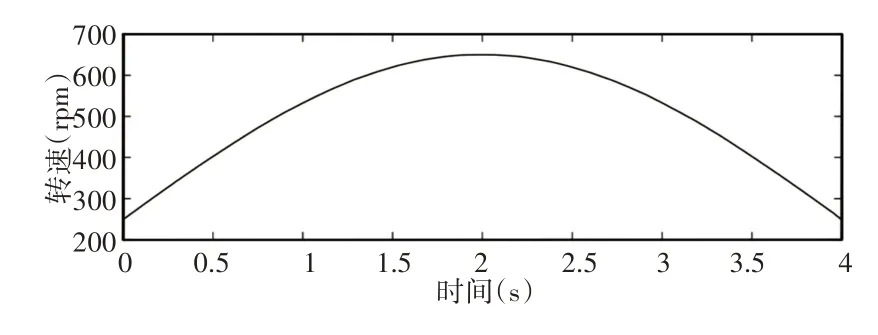
图3 速度曲线Fig.3 Velocity Curve
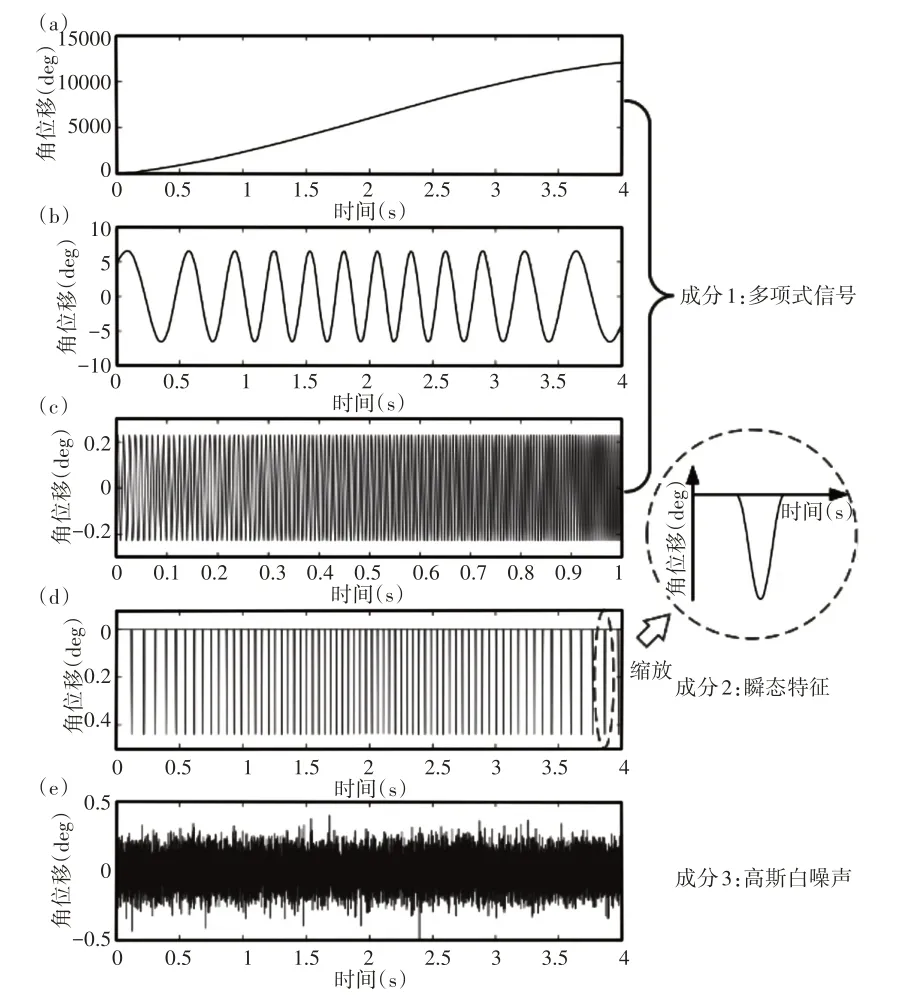
图4 模拟的编码器信号Fig.4 Simulated Encoder Signal
(e)高斯白噪声此外,从角度瞬变的放大视图中可以发现,稀疏的大振幅值趋向于形成一个群,称为瞬变特征的群稀疏性。在加入方差为0.1的高斯白噪声后,合成编码器信号,如图5所示。然而,编码信号中的累积角位置占主导地位,瞬态特征不可见,因此无法根据原始编码信号直接识别健康状况。
图5 合成编码器信号Fig.5 Synthesis Encoder Signal
4.2 参数选择
在本节中,将讨论一种自适应参数选择策略,以自动选择所提出方法LPFSA-OT算法的合适参数。
(1)块长度L,重叠长度P和多项式次数d
为了尽可能多近似多项式信号p(t),同时防止近似瞬态特征x(t),每个长度为L的块必须包含几个齿轮啮合周期,这意味着L满足L=[N*fs/fm],其中N是周期的个数,fs和fm表示采样频率和啮合频率。注意,啮合频率fm是根据变速条件下行星齿轮箱的最小转速vmin计算的。最小旋转速度vmin的计算过程简述如下。由于编码器信号记录了编码器轴的角位置,因此首先通过计算原始编码器信号的一阶差分来获得瞬时转速。此后,应用移动平均滤波器以进一步去除包含在瞬时瞬时转速中的干扰分量,从而获得平滑的瞬时转速曲线。最后,通过确定平滑的瞬时转速的最小值,可以容易地获得最小转速vmin。
在传统的局部多项式拟合中,窗口移动了一个点,即相邻块之间的重叠长度P为L-1,这不可避免地增加了计算复杂度。将重叠长度P设置为[0.75*L],可以同时降低计算复杂度,并保证所提出方法LPFSA-OT的良好性能。为了获得令人满意的近似值,通常建议将多项式度数d设为较大的值。但是,较大的多项式次数通常会导致过度拟合和数值不稳定。在数值模拟和实际应用的基础上,发现3-7的多项式度数d适合于编码器信号分析。因此,这里采用d=5。
(2)组大小K,惩罚参数μ,迭代次数iter
为了提高瞬态特征的群稀疏性,建议将组大小K设置为3-15,并采用K=10。此外,应当指出,K的上限可以随着采样率的增加而增加。惩罚参数μ是一个正标量,仅影响算法收敛到全局最优值的速度,因此可以将μ选为常数,建议μ=1.0。由于优化问题的凸性,可以在几次快速迭代后获得最优解。在这里,将迭代次数iter设置为50,这可确保在节省计算时间的同时获得最佳解决方案。
(3)正则化参数λ
正则化参数λ用于保持数据保真度之间的平衡,并且对最终结果有很大的影响。因此,选择适当的参数λ以说明从原始编码器信号y(t)提取时域瞬态特征x(t)很重要。针对该问题,提出了谐波噪声比指导的正则化参数选择策略。HNR是指示信号z周期性的度量,当z是无噪声的周期性信号时,HNR趋于无穷大,定义为:

式中:γ—信号z的自相关函数,而τmax—具有局部最大值的滞后,如图6所示。由于所提出的方法LPFSA-OT算法的目的是突出故障引起的瞬态特征并且瞬态特征在角域中具有很高的周期性,因此将与角域瞬态特征x(θ)的最大HNR相对应的参数λ考虑为最佳值。
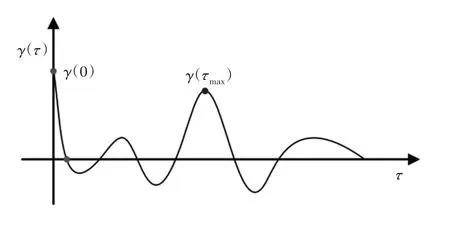
图6 信号z的自相关函数Fig.6 Auto-Correlation Function of Signal z
4.3 效果评估
图7给出了由一阶差分和移动平均滤波器获得的平滑瞬时转速曲线,从中可以确定最小转速为252rpm。因此,将块长度L设置为其中6是周期数N,20表示齿轮啮合引起的谐波分量的谐波阶次为q2。相应地,重叠长度P被设置为为了进一步确定最优λ,图8中给出了相对于λ的HNR曲线。如图8所示,随着参数λ的增加,HNR单调增加,直到达到临界点为止。(λ=0.42,HNR=1.151)。但是,当λ继续增加时,HNR逐渐减小。因此,确定与最大值HNR相对应的最优值λ=0.42。

图7 估算的瞬时转速曲线Fig.7 Estimated Instantaneous Speed Curve

图8 度量HNR与正则化参数λ之间的关系Fig.8 Relationship Between Metrics HNR and Regularization Parameters λ
图9给出了通过提出方法获得的结果,其中参数设置为L=357,P=267,d=5,K=10,μ=1,iter=50,λ=0.42。多项式信号p(t)和时域瞬态特征x(t)如图9(a)和(b)所示,从中可以发现这两个分量已从原始编码器信号中成功提取。尽管如图9(b)所示,可以清楚地检测到时域的瞬态特征,但由于速度变化,瞬态并不均匀分布,这给识别故障类型带来了困难。为了解决这个问题,采用阶跃跟踪技术以恒定的角度增量对时域瞬态特征进行重采样。在此过程中,多项式信号p(t)被选作参考轴的瞬时相位。重新采样的瞬态特征显示在图9(c)中,从中可以发现速度变化的影响已被有效消除,并且瞬态特征x(θ)在角域中是周期性的。为了进一步识别相邻瞬变的间隔,图9(d)给出了几个瞬变的放大图。可以看出,瞬变等距间隔了180°,这对应于角域中的预定义故障周期。结果表明,LPFSA-OT成功实现了变速箱行星齿轮箱的故障检测,进一步证实了编码器信号在状态评估中的可行性。此外,图10示出了(15)中的目标函数J(x,ɑ)的历史,其中,在多次迭代之后目标函数达到最小值。以上结果表明,该方法可以快速收敛到全局最小值。
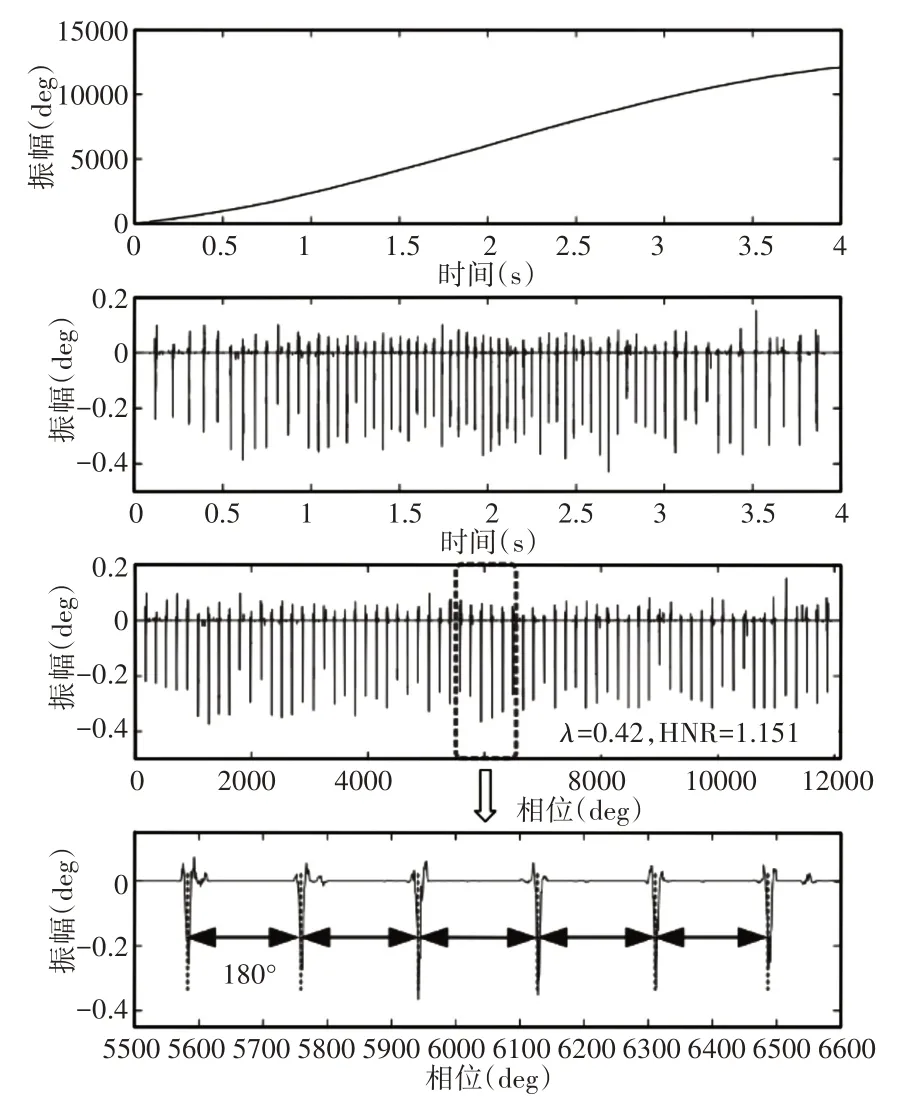
图9 提出方法获得的结果Fig.9 Results Obtained by the Proposed Method
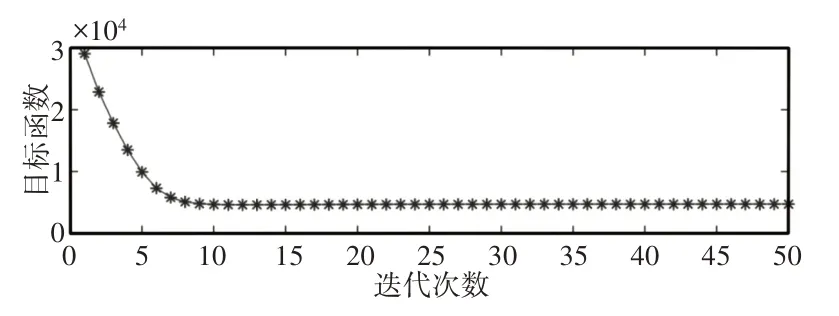
图10 目标函数J(x,ɑ)的历史Fig.10 History of Objective Function J(x,ɑ)
为了清楚地评估参数λ对所提出的方法的性能的影响,在图11中显示了在不同参数下提取的角域瞬态特征x(θ)。人们可以发现噪声分量并未得到有效去除。当参数λ设置为0.26时,小于临界点0.42。而且,当参数λ超过临界点0.42时,瞬态特征变得稀疏并且难以识别。因此,可以合理地得出结论:HNR引导的正则化参数选择策略为确定合适的参数λ提供了可靠的工具。
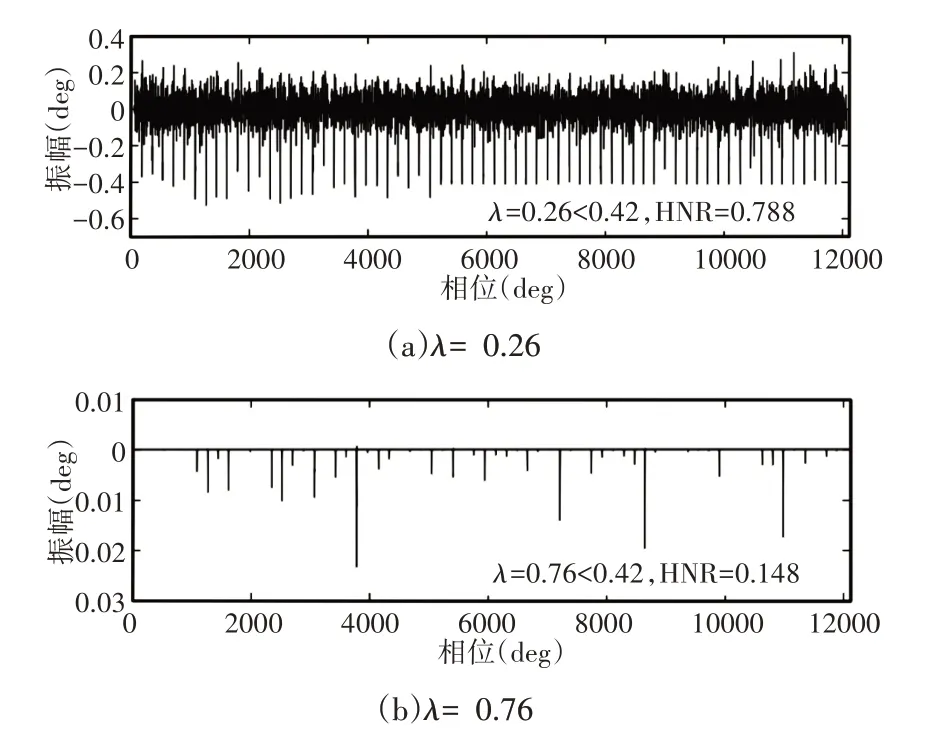
图11 通过提出方法获得的具有不同正则化参数λ的提取角域瞬态特征Fig.11 Extracted Corner Domain Transient Characteristics with Different Regularization Parameters Obtained by the Proposed Method
为了进一步揭示LPFSA-OT的优越性,还通过基于奇异值分解(SVD)的方法分析了合成编码器信号。在基于SVD的方法中,首先使用奇异值分解获得时域中的一系列位置分量,然后通过顺序跟踪技术将这些时域中的位置分量转换为角域中的位置分量。与提出的方法不同,原始编码器信号y(t)被选作相位参考信号进行信号重采样。出了时域和角域中的前5个位置分量,如图12所示。根据分解结果,可以发现瞬态特征被分解为
第二至第四位置分量。时域中的位置成分、在角域中的位置分量然而,如图12(a)、图12(b)所示。瞬态特征表现出较大的失真,并受到其他干扰分量的强烈干扰,这不可避免地增加了识别被监控设备健康状况的难度。上述结果表明,当对从在变速条件下运行的行星齿轮箱获取的编码器信号执行基于SVD的方法时,很难获得令人满意的结果。
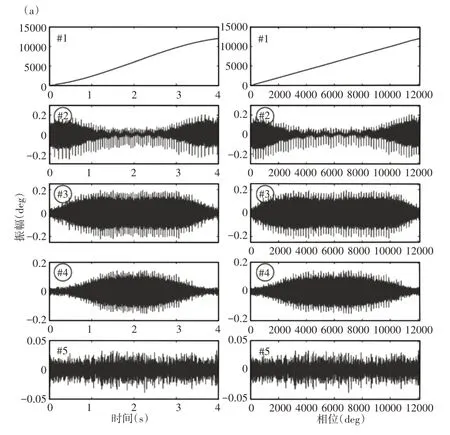
图12 通过基于SVD的方法获得的结果Fig.12 Results Obtained by SVD Based Approach
5 实验验证
在本节中,通过从以变速状态运行的行星齿轮箱获取的实际编码器信号进一步证实了LPFSA-OT的有效性。实验装置如图13(a)所示,它由驱动马达,行星齿轮箱,电磁制动器和两个旋转编码器组成。磁性断路器用于在输出轴上加载,旋转编码器用于收集编码器信号。此外,在实验过程中,手动调整了电机控制器,并且转速经历了加减速过程。图13(b)展示了行星齿轮箱的详细结构,该行星齿轮箱包含20齿的太阳轮,82齿的齿圈和31齿的三个均匀分布的行星齿轮。请注意,当太阳轮和行星架分别连接到输入轴和输出轴时,齿圈静止。根据行星齿轮箱的配置参数,计算出与输出轴有关的故障顺序,并在表1中列出,其中fs,fp,fr分别代表太阳轮,行星齿轮和齿圈的故障顺序。此外,齿轮啮合频率fm为82fo,其中fo为输出轴的旋转频率。这里分析了以5000Hz采样频率从输出编码器收集的编码器信号,以对行星齿轮箱进行状态监测。

图13 实验装置、行星齿轮箱的示意图Fig.13 Experimental Setup,Schematic Diagram of Planetary Gearbox

表1 行星齿轮箱相对于输出轴的故障顺序(Hz)Tab.1 Fault Sequence of Planetary Gearbox Relative to Output Shaft(Hz)
散齿是行星齿轮箱的常见故障类型。为了模拟该故障,将图14所示的带散齿的齿圈装配到行星齿轮箱上。在图15中显示了在变速条件下收集的原始编码器信号。但是,由于累积的角度位置分量在原始编码器信号中占主导地位,因此没有发现明显的瞬态特征。

图14 齿圈上的裂齿Fig.14 Split Teeth on Ring Gear

图15 原始编码器信号Fig.15 Original Encoder Signal
为了有效地提取瞬态特征,将所提出方法应用于原始编码器信号。瞬时转速曲线,如图16所示。从该瞬时转速曲线确定了160.4rpm的最小转速vmin。根据自适应参数选择方案,将几个参数设置为μ=1,iter=50。度量HNR和正则化参数λ之间的关系,从中可以确定对应于最大HNR的最佳参数λ=0.16,如图17所示。通过提出方法获得的结果,如图18所示。图18(a)和图18(b)显示了多项式信号p(t)和时域瞬态特征x(t),从中可以发现齿轮故障引起的角瞬变清晰可见。为了进一步识别出哪个组件有故障,将时域中的非平稳瞬态特征转换为角域中的平稳瞬态特征,如图18(c)所示。从图18(d)的局部放大细节中,可以检测到间隔为120°(即360/fr)的独特瞬态特征,这为行星齿轮存在故障提供了有力的证据。
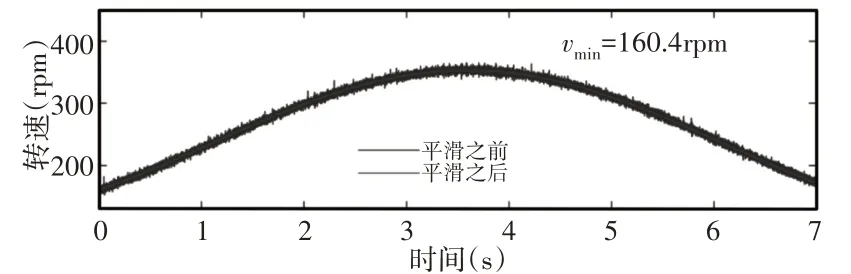
图16 瞬时转速曲线的估算Fig.16 Estimation of Instantaneous Speed Curve
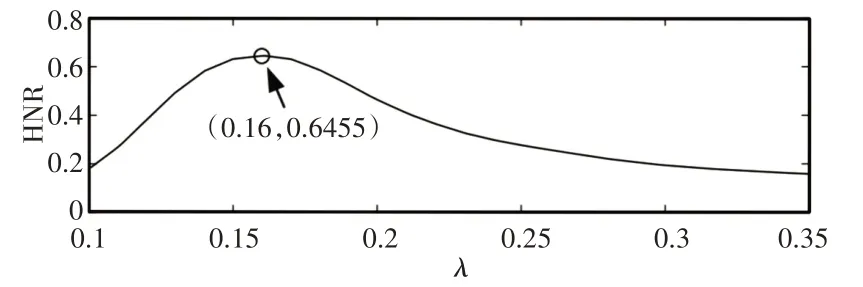
图17 度量HNR和正则化参数λ之间的关系Fig.17 Measures the Relationship Between HNR and Regularization Parameters λ
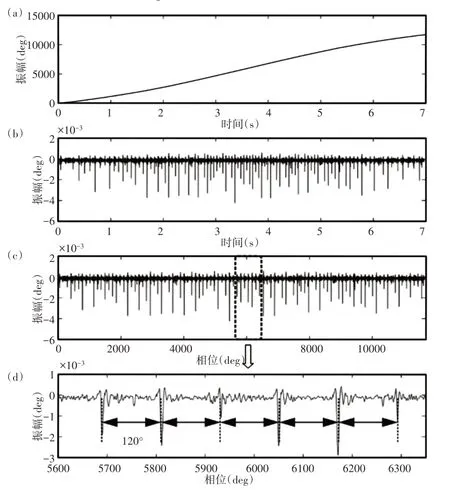
图18 提出方法获得的结果Fig.18 Results Obtained by the Proposed Method
另外,基于SVD的方法也用于相同的编码器信号,其结果如图19所示。时域中的位置成分、在角域中的位置分量,如图19(a)、图19(b)所示。通过检查分解结果,发现瞬态特征主要分解为第二和第三位置分量。为了清楚起见,第二和第三位置分量的局部放大图,如图20所示。瞬变特征被其他分量严重阻碍,这使得很难识别故障引起的角瞬变,尤其是第三和第六角瞬变。因此,与所提出的方法相比,基于SVD的方法无法有效提取瞬态特征。
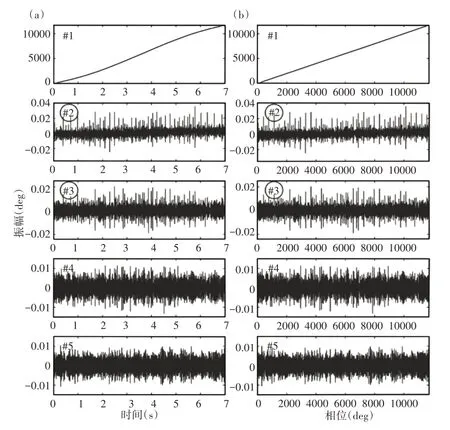
图19 通过基于SVD的方法获得的结果Fig.19 Results Obtained by SVD Based Method
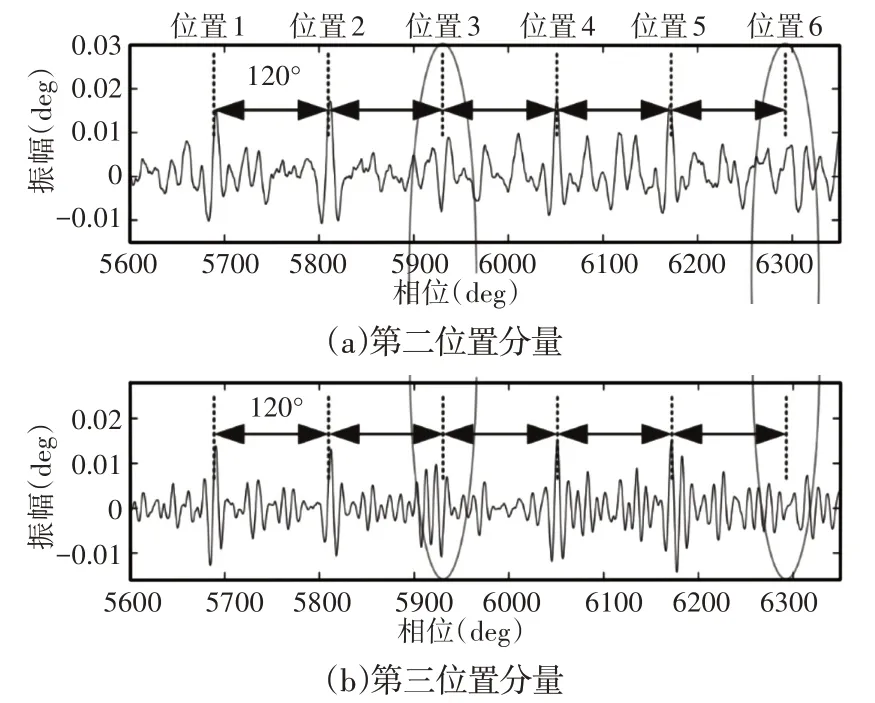
图20 范围(5600~6350)°的放大图Fig.20 Enlarged View of the Range(5600~6350)°
6 结论
针对变速齿轮箱时变故障检测问题,提出了一种基于LPFSA与阶次跟踪的变速齿轮箱编码器信号瞬态特征提取算法。通过仿真和实验结果可得出如下结论:
(1)局部多项式拟合稀疏算法能够有效的从原始编码器信号中提取与齿轮故障相关的时域瞬态特征。且提出的迭代优化算法能够迅速收敛。
(2)阶跃跟踪技术以恒定的角度增量对时域瞬态特征进行重采样,可以消除速度变化造成的影响,实现时变转速条件下的故障检测。
(3)与基于奇异值分解的方法相比,LPFSA-OT能更准确地提取暂态特征,成功实现了变速箱行星齿轮箱的故障检测,进一步证实了编码器信号在状态评估中的可行性。
