基于状态空间的轮系功率流分析方法研究
2022-11-11李胜甲姜小蛟马雅丽蒲大君李灿灿
李胜甲,姜小蛟,马雅丽,蒲大君,李灿灿
(大连理工大学机械工程学院,辽宁 大连 116024)
行星轮系因具有速比高、体积小、精度高、质量轻、效率高等优点,在自动变速器等机械传动领域得到了广泛的应用[1]。而在行星齿轮传动的方案设计中,行星轮系的功率流向直接影响着整个行星轮系传递效率的大小,因此在行星轮系的选用、设计以及分析过程中,要特别注意轮系中的功率流动问题。行星轮系的功率流根据流向的不同可分为两类——分流型和回流型,其中回流型功率流因在轮系内部存在循环流动,功率就像被封闭一样,也可称为封闭功率流。封闭功率流的存在将会造成能量浪费,降低轮系性能,因此在轮系设计中避免产生封闭功率流是设计中要重点考虑的问题之一。Chen[2]引入虚功理论对复杂轮系的功率分流进行了研究,并推导了基于虚功原理的分析方法;Cui等[3]提出了多属性拓扑图的概念,用来表征单自由度平面直齿封闭行星轮系的结构和状态特征,并在轮系的功率流分析上进行了应用,提供了一个图形视图用于显示功率流;周新涛等[4]将信号流图的理念引入到单自由度行星齿轮系统中,用以解决复杂行星齿轮传动系统中的相关特性参数,为其运动参数的分析提供了一条新的思路;徐琳等[5]针对环路式复合行星齿轮系统中存在的多种功率流类型,提出了复合式杠杆分析法,实现了功率流类型的定性判断。
国内外学者虽然提出了很多种分析方法,但是在计算简易程度以及应用范围上还存在一定的局限性,不利于用计算机编程实现通用化,因此在复杂轮系功率流的设计分析方面还有很大的研究空间。马雅丽[6]提出了一种基于特征状态空间的机械运动方案设计理论与方法,该方法实现了机械系统运动方案设计向特征状态空间的数学模型转化。本文在其基础上,以状态空间理论为引导,基于特征状态方程以及轮系基本单元的连接约束方程中非零元素及其之间的制约关系,提出了一种分析行星轮系功率流的简便方法,为利用计算机编程实现复杂结构轮系的功率流分析提供理论依据。
1 行星轮系功率流分析的理论基础
对于包括轮系在内的机械系统而言,功率的输入与输出有着以下特点:输入功率端的转矩T与角速度ω两者方向是相同的,而输出功率端两者方向则相反。故而,可以用转矩T和角速度ω乘积的正负来判断行星轮系中两相邻基本单元结合点的功率方向,以此来确定在该轮系中是否存在功率回流。这就要求在用此种方法进行功率流分析时需要将输入功率端与输出功率端的角速度与转矩计算出来。但在进行复杂轮系结构方案设计过程中,由于存在轮系结构不确定性等诸多因素,因此该方法就显得费时费力。基于此,本文提出了一种基于状态空间理论来判断轮系功率流向的新方法,该方法利用复杂轮系的可拆分性及在功率传递中运动特征与动力特征的变换规律,来完成轮系功率流向的判别,可起到在行星轮系方案设计阶段节省设计时间、加快设计进度的效果。
轮系基本单元[7]是复杂轮系的基本组成部分。任何复杂轮系在经过拆分之后,都可以看成是由两个或两个以上轮系基本单元按照一定的组合方式连接而成。轮系基本单元实现运动变换及动力变换的实质是实现运动特征和动力特征的变换。这里用向量e表示轮系中基本单元的特征矢量,e=(ωT)T,其中角速度ω=(ωx,ωy,ωz)T,描述轮系基本单元的运动特征,转矩T=(Tx,Ty,Tz)T,描述轮系基本单元的动力特征。
1.1 轮系基本单元的状态空间方程
基于轮系状态空间理论的基本单元分析方法,其重点在于研究轮系中输入端与输出端之间的特征状态变换关系,而对系统内部的状态不做分析。轮系基本单元的状态空间方程是描述复杂轮系中某一个基本单元的输入端与输出端的运动特征及动力特征的映射关系表达式。由于基本单元中输入、输出构件的运动特征及动力特征均存在一一对应的线性关系,且这一线性关系可以用一个二阶矩阵At来表示,其中t表示轮系中的第t个基本单元,∀t=1,2,…,n。因此,轮系基本单元的输入状态矢量空间ei与输出状态矢量空间eo之间的关系方程可表示为eo=At·ei,该方程称为轮系基本单元的状态空间方程[6]。
1.2 轮系基本单元的连接约束方程
轮系由基本单元连接组合而成,这一理念是轮系基本单元分析法的核心。而基本单元的组合过程则是方程中引入特征约束的过程。轮系基本单元的连接约束方程[6]是描述轮系中相邻接的两个单元之间连接关系的式子。相邻两基本单元的结合位置称为单元结合点。假设前置轮系单元j的输出与后置轮系单元(j+1)的输入相连接,约定上标i和o分别代表单元的输入和输出,则有:
(1)
式中:Cj(j+1)为单元之间的连接约束矩阵。


2)联接构件轴向位置不同。两构件轴向位置不同时,分析其动力特征,并列出动力平衡方程,可得到动力特征的约束矩阵为:
(2)
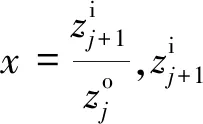
2 行星轮系的功率流分析方法
轮系的功率流向由表征能量状态特征空间的动力特征T和运动特征ω来确定,利用前述基本单元的状态模型来研究轮系的功率流向问题,是简化轮系功率流分析方法的有效途径。因此,对复杂轮系功率流问题的分析就是根据连接约束模型确定单元结合点的连接形式,并根据前置单元与后置单元的特征状态模型描述单元结合点的运动状态及动力状态,进一步分析、判断单元结合点的功率流向,进而对整个轮系进行功率流向描述。
基于轮系基本单元的状态空间理论,利用轮系基本单元中状态方程与基本单元组合的连接约束方程中的非零元素所表征的单元及单元之间运动特征和动力特征之间的关系,以及前置和后置单元中已知的运动特征与动力特征去描述轮系基本单元结合点的能量状态特征,形成特征矢量,然后根据该特征矢量空间去判断轮系中单元结合点的功率流流向,最终得到轮系的功率流流向。用数学语言对其描述如下。
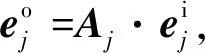
(3)
式中:ωQ和TQ分别为Q点的运动特征和动力特征。
当ωQ×TQ>0时,结合点处为输入功率,说明轮系中出现功率回流;当ωQ×TQ<0时,结合点处为输出功率,即轮系中没有出现功率回流。
3 轮系功率流分析实例
以图1所示的某风机减速器为例,用该方法对其轮系的功率流进行分析。如图所示,输入构件为齿轮1,输出构件为行星架H。
1)拆分轮系。
将图1所示的复杂轮系从电机到风叶拆分为4个轮系基本单元,如图2所示。

图1 某风机减速器

图2 拆分后的基本单元
2)建立模型。
依据轮系基本单元库[8],可写出4个单元的状态空间方程分别为:
(4)
(5)
(6)
(7)
式中:zi(i=1,2,…,7)为图1中各个齿轮的齿数。
则单元1、2,单元2、3,单元3、4之间的连接约束方程分别为:
(8)
(9)
(10)
3)结合点特征状态向量叠加。
单元1、2和单元2、3之间均是前置单元的输出直接与后置单元的输入相连接的情况,不存在功率回流,所以只需要考虑单元3、4之间的结合点。单元3、4中,结合点Q的特征状态向量表述形式分别为:
(11)
(12)
式中:ωj_i为第j单元构件i的角速度;Tj_i为第j单元构件i的转矩。
由连接约束方程可知,ω3_H=ω4_H,T3_H=-T4_H。将式(11)、式(12)叠加整合,则有:
(13)
(14)
4)结合点的功率流向分析。
若z1=24、z2=30、z3=22、z4=34、z5=20、z6=17、z7=72,设轮系输入转速ω1=15 r/min,转矩T为100 N·m。经过计算,可得到:ωQ<0,TQ<0,故有ωQ·TQ>0,据此即可分析得出该轮系在结合点Q处出现功率回流,所绘制的功率流如图3所示。
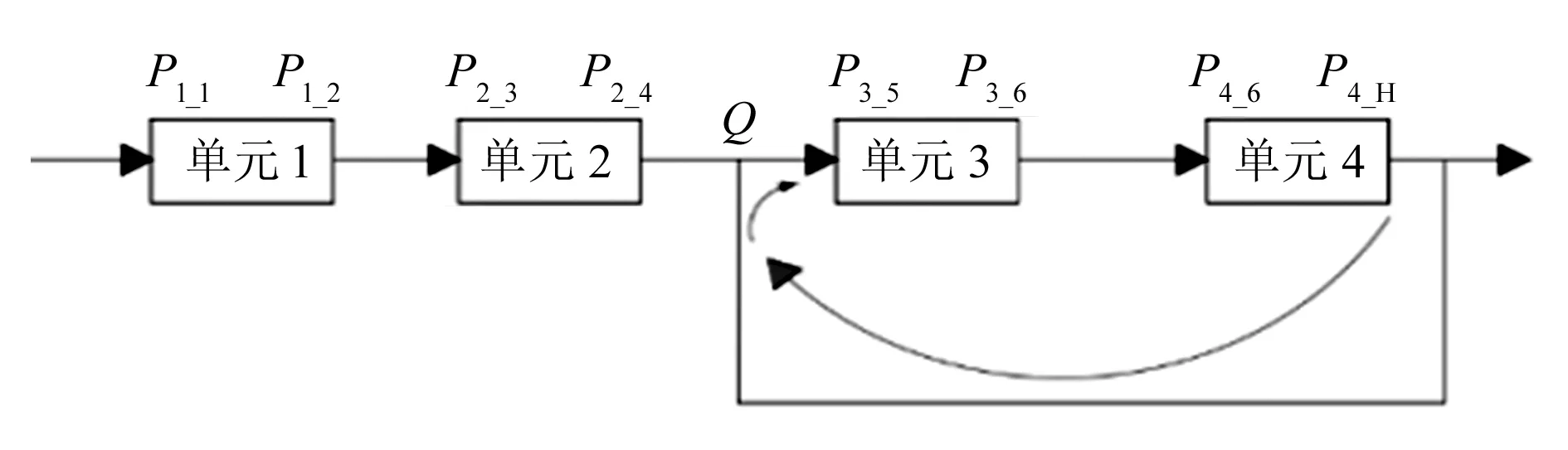
图3 轮系功率流图
4 结论
本文基于状态空间理论,建立了对复杂行星轮系功率流分析的完整流程和方法,并以某风机减速器为例,实现了轮系功率流流向的判断,结果表明:
1)将复杂轮系拆分为轮系基本单元,对轮系基本单元进行分析,从而实现对复杂轮系的分析,证明了单元分析方法是进行轮系功率流分析的有效方法;
2)建立相应轮系单元的特征状态方程与基本单元之间的连接约束方程,进行向量叠加可以获得单元结合点状态向量中各元素的理论值;
3)根据各轮系基本单元的内部功率流向和单元结合点处的功率流向,可以有效判断出复杂轮系的功率流情况。此方法可为轮系运动方案设计提供模型支撑,并为轮系的数字化分析与综合评价提供理论依据。
