不同冲击度约束下智能汽车换道轨迹优化

邓召文，乔宝山，袁显举，冯 樱

（湖北汽车工业学院汽车工程学院，湖北 十堰 442002）

1 引言

集环境感知、规划决策、自动驾驶等多种功能于一体的智能车辆可大幅提高现代交通系统的安全性和解决交通堵塞问题。车道变换和车道跟驰是车辆行驶中两种典型的运行模式，研究人员对车道跟驰模型已开展了50多年的研究，而换道模型研究起步相对较晚。这是因为跟驰模型只需考虑前后两辆汽车，而车辆换道是二维平面运动，需要考虑更多的周围车辆，所以换道模型更为复杂和具有挑战性［1］。换道轨迹的生成是实现换道安全、舒适和高效的前提条件，换道过程中运动参数变化量与换道轨迹直接相关，通常采用车辆的冲击度来衡量汽车变道过程中舒适性。所谓冲击度是指汽车做非匀速运动时加速度的导数值，其取值范围的大小一直模糊不清。

具有相对直观、精确度高、运算量小等特点的几何算法是换道轨迹规划主要采用的算法。常见的有等速偏移法、圆弧轨迹法、余弦函数法、正反梯形侧向加速度轨迹法、余弦函数、双曲正切函数加权法及上述方法的叠加［2］和多项式法等。多项式轨迹法形式简单、曲率连续，便于算法扩展，已出现有3次多项式、5次、6次或7次多项式等。文献［3］在对美国下一代交通仿真（NGSIM）车辆轨迹数据研究中指出当多项式阶次≥5，车辆变道轨迹的平均拟合优度已达0.99，阶次再提高，将导致计算量增大较快。换道轨迹规划需要考虑周围车辆、自车运动学及动力学等约束，文献［4］建立了前方有障碍物的换道模型，文献［5］提出轨迹规划要考虑加速度的限制，文献［6］引入安全控制系数，对不同安全控制系数的换道轨迹进行分析，文献［7］提出了一种自动车辆换道轨迹规划方法。但综合考虑相邻车道的交通状况，对换道轨迹的综合寻优规划研究还有待深入。

在考虑本车道前方有障碍车辆，目标车道有高速行驶车辆的工况下，以5次多项式方法对智能汽车避撞换道进行轨迹设计。兼顾碰撞安全距离、车辆运动学与动力学约束，建立满足安全、舒适和高效条件的目标函数，采用序列二次规划算法进行优化求解，探讨不同换道模式下的冲击度约束设置问题。

2 换道模型

智能驾驶车辆在行驶过程中，由车载雷达、摄像头或车联网获取外部实时信息，结合自车的车速及相对位置，根据周围驾驶环境，决定换道还是车道保持或者停车制动。

2.1 换道场景定义

换道场景设计，如图1所示。自车S在原车道低速行驶，假设前方有一静止障碍车PB；左侧为目标车道，前后两车PA和FA以较高车速等速行驶。自车S在原车道行驶时，当发现汽车PB时，自车有避障和继续行驶的驾驶需求，在保证安全、舒适的前提下，将按照规划的轨迹进行换道，并插入目标车道的运动的PA、FA两车之间。车辆PA、PB的位置用其尾部中点位置来表示，车辆FA的位置用其前部中点的位置表示，假设自车的质心位于车辆的中心，用质心位置表示S车的位置。

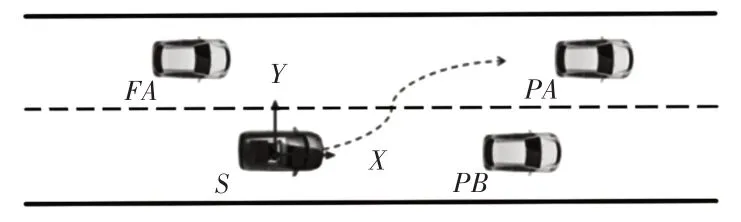
图1 换道场景Fig.1 Lane-Changing Scenario

2.2 换道轨迹函数

2.2.1 换道轨迹运动状态

假定自车S从t0开始，在时间tf内完成从原始车道到目标车道的换道，以x0、y0、xf、yf表示自车在换道起始和结束时刻位置。换道轨迹函数用基于时间的5次多项式来构造［8］，如式（1）所示：

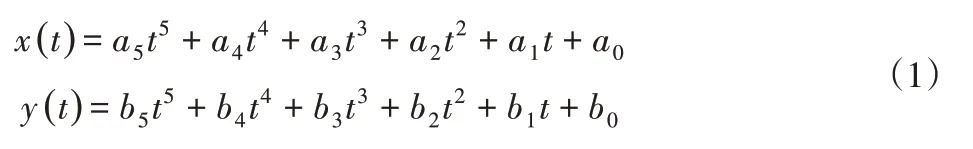
自车换道初始和终了的位移、速度及加速度可表示为：

假设初始位置、速度和加速度已知，且换道结束时刻的纵向和侧向加速度为零、侧向速度为零，纵向速度为目标车道的平均速度。对式（1）分别求一阶和二阶导数，可得到换道过程中的速度及加速度函数，将初始及终了时刻的运动参数值代入后，可得到式（2）。

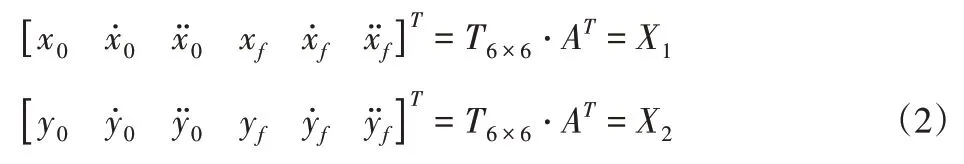
式（2）中的时间参数矩阵T6×6为：

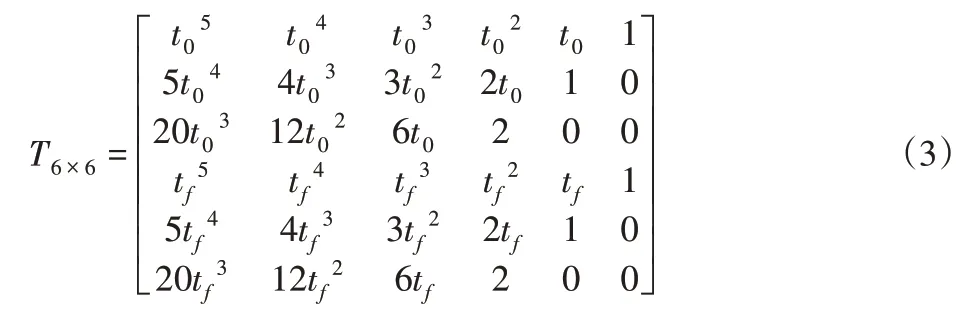
系数向量A、B分别为：

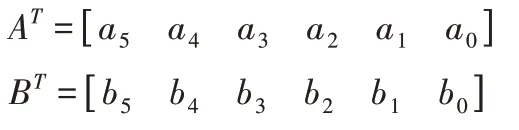
将换道初始时刻t0设为0时刻，需要确定换道结束时间tf和纵向位移xf。tf和xf求出后，系数向量A、B可用式（4）求解。

2.2.2 约束条件

（1）安全性约束

首先，从安全性考虑，换道时自车不能超越道路边界。换道过程中，自车在原始车道中心线和目标车道中心线之间运动，设W为车道宽，侧向位移要满足式（5），即：

其次，自车的纵向速度不能超过所在车道允许的最高车速vx，max，且保持正值，即不能停车也不能倒车，即：

最后，在换道过程中，要避免碰撞，自车还要与其它车辆保持足够的安全距离，即需要考虑自车与本车道前方车辆PB和目标车道前后车辆PA、FA之间的安全距离。式（7）到式（9）是保证换道过程中自车与周围车辆不发生碰撞的约束条件［9］。

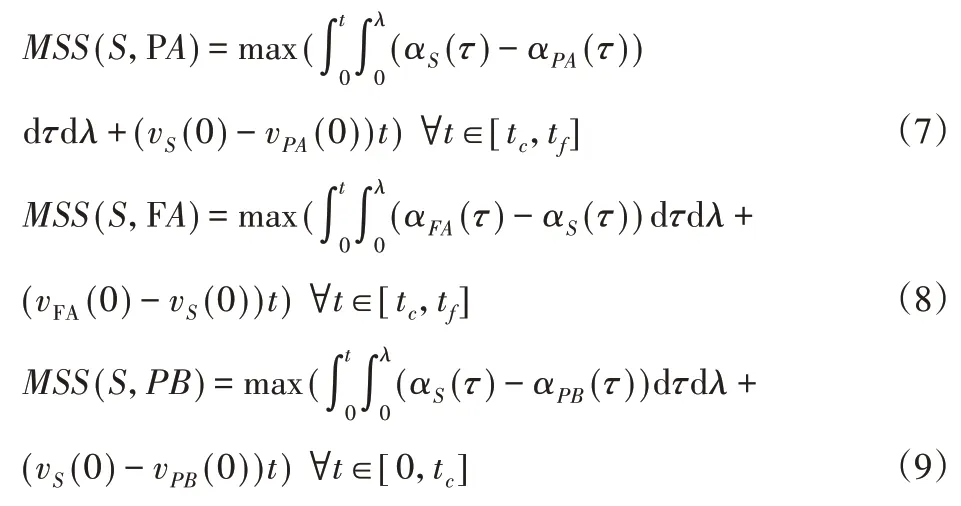
式中：αi和v i—换道场景中各车的加速度和速度值tC—自车与周围车辆发生碰撞的时刻。考虑到汽车紧急制动等因素，各车之间还应预设一个安全距离d0，则式（7）～式（9）可写成：

（2）舒适性约束

为了保证换道平顺、舒适，换道过程中自车纵向和侧向加速度和冲击度不仅要满足汽车动力学的要求，还应控制在一定范围内，即：

式中：ɑx，max=min(μg，ɑx，driver)，ɑx，driver—换道过程中驾驶员所希望达到的最大纵向加速度值ɑy，driver—驾驶员期望最大侧向加速度值；jx(t)、jy(t)—纵向和侧向冲击度。

2.2.3 优化目标函数

要实现高效、舒适的换道操作，一方面希望智能汽车纵向和侧向冲击度尽可能小，换道平顺，但会增加换道时间和距离，原始车道和目标车道的交通效率也会随之降低，综合考虑，目标函数为：

式中：w1、w2、w3—纵向、侧向冲击度和换道结束纵向位移的权重系数；k—常数；W—车道宽。

3 优化求解

3.1 SQP非线性优化方法

式（1-12）为非线性目标函数，受到多个不等式约束，为典型的非线性优化求解问题。常用求解方法有：内点罚函数法、序列二次规划法和信赖域反射法。序列二次规划法（SQP算法）具有边界搜索能力强，收敛性好、计算效率高的特点，其以Lagrange-Newton优化方法为基础，属于“不可行”算法，即该算法产生的迭代点不一定是可行点［10］。对于上述优化问题可表达为：

式中：f(x)—连续可微凸函数；D—Rn中的一个非空子集，A∈Rm×n，b∈Rm。

非线性约束最优化问题通过SQP算法可转化为较简单的二次规划（QP）问题，主要求解步骤：

（1）采用二次泰勒级数对当前点xk进行展开，得：

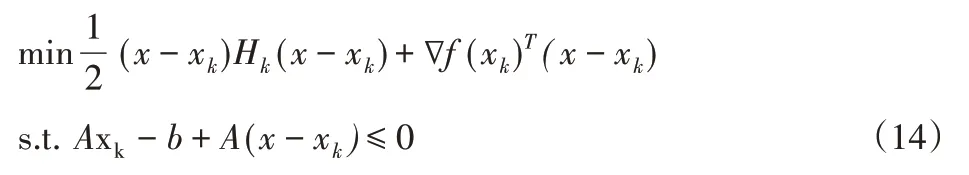
式中：∇f(xk)—f(x)在xk点处梯度；Hk—f(x)在xk点处Hessian矩阵的正定拟牛顿近似值。

（2）用二次规划算法求解上式，可得到x-xk；

（3）令dk=x-xk，进行下一步迭代，得到新优化点，xk+1=xk+αkdk。

式中：αk—步长，可通过线性搜索获得。

3.2 优化变量求解界面设计

为了便于分析驾驶环境和约束条件变化对换道时间和换道距离的影响，利用Matlab的图形用户界面模块设计换道轨迹规划界面，如图2所示。在该界面包含输入和输出两部分，输入部分的场景设置可通过键盘定义本车道和目标车道的车辆的位置、速度等参数；约束条件包括纵向和侧向的速度、加速度及冲击度范围，单位为国际制单位；界面中的权重系数w1、w2、w3如上所述。

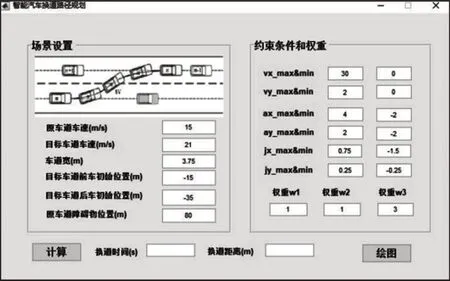
图2 换道路径规划GUI界面Fig.2 GUI Interface of Lane-Change Planning

4 设计结果与分析

4.1 场景条件设置实例

自车在原车道行驶车速为15m/s，目标车道上车辆以21m/s的速度匀速行驶；自车当前位置记为（0，0）m，前方障碍车辆的位置为（80，0）m，目标车道前车位置（-15，3.75）m，后车位置（-35，3.75）m，两车的间距为20m。自车在换道过程中纵向速度约束范围（0，30）m/s，侧向速度约束范围（0，2）m/s，纵向加速度约束范围（-2，4）m/s2，侧向加速度约束范围（-2，2）m/s2，纵向冲击度约束范围（-1.5，0.75）m/s3，侧向冲击度约束范围（-0.25，0.25）m/s3，权重系数w1、w2、w3分别为1、1、3。点击图2界面的“计算”按钮，可计算得到的换道时间和换道距离；点击“绘图”按钮可得到换挡过程中自车的换道轨迹和整个换道过程中的速度、加速度和冲击度随时间变化曲线。

4.2 换道轨迹结果与分析

不同驾驶环境下的换道轨迹参数和部分运动参数的极值，如表1所示。第1列为前方障碍车PB与自车的距离，第2、3列tf、xf为优化计算得到的换道时间及纵向位移，SPA、SFA分别为车辆PA和FA在tf时刻的纵向位置，后面各列为自车在换道过程中的速度、加速度和冲击度极值。表1中第2行是上述实例的计算结果：当前方80m处有障碍车，自车实现换道时间为9.56s，换道结束自车纵向位移为170.96m。换道过程中自车的速度、加速度以及冲击度的极值均满足约束要求。目标车道前车PA纵向位移为185.76m，后车FA纵向位移为165.76m，自车位于两车之间，且与二者保持安全距离，但相对靠近后车。有研究指出高速公路换道耗时一般在（3.5～8.5）s之间，9.5s的换道时间在汽车实际换道中耗时偏长，说明所设置的某些动力学约束条件设置相对苛刻。

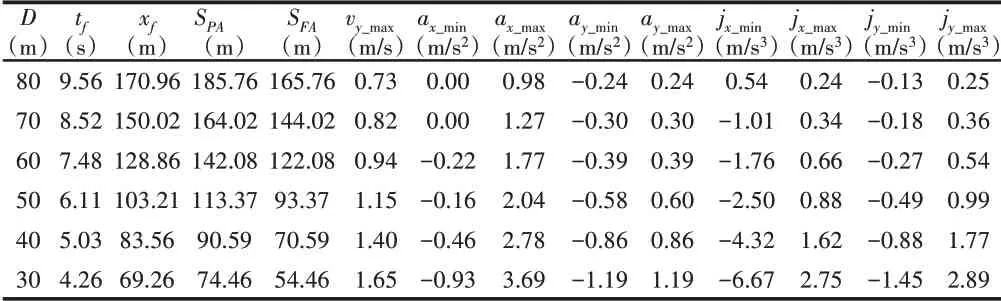
表1 前方障碍距离不同时换道轨迹参数Tab.1 Lane-Change Track Parameters in Difference Distances between Self Vehicle and PB

可以通过改变前方障碍车的位置，保持图2中其它设置不变，来研究各约束条件对换道时间或换道距离位置的影响。将自车与前方障碍距离分别设置为70m、60m、50m、40m、30m。通过优化计算，能得到相应的换道时间和换道位移，不同障碍距离的换道轨迹曲线，如图3所示。

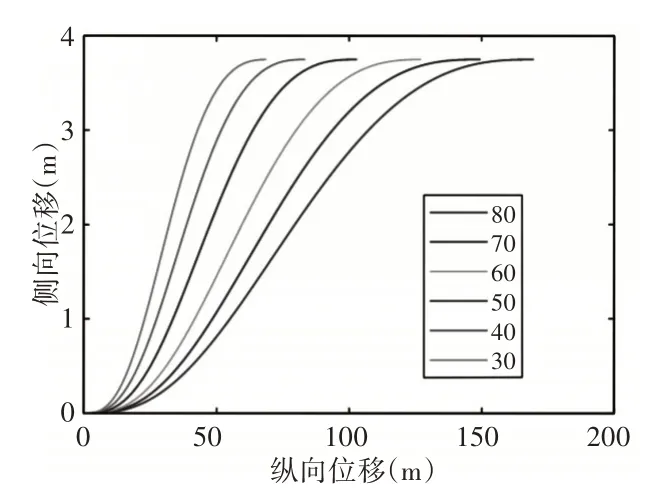
图3 不同障碍距离的换道轨迹Fig.3 Trajectories of Different Obstacle Distances

其对应的轨迹运动参数列于表1各行中，从表1可见，障碍车与自车距离越近，自车换道时间和位移以及PA和FA车位移都会随之缩短，自车在插入目标车道两车之间时，纵向方向的提速会更快，即更接近前车的尾部。不同障碍距离时自车换道过程速度、加速度和冲击度曲线，如图4所示。可见随着换道时间的缩短，相应侧向和纵向速度、加速度和冲击度变化越大。

表1数据显示当前方障碍物距离变小时，虽然轨道优化程序依然能得到计算结果，但冲击度的约束不再满足。图4显示当前方障碍为30m时，要完成换道，纵向冲击度最大值为6.67m/s3，侧向冲击度最大值为3m/s3，这说明序列二次规划方法具备约束外求极值的功能。现实中即使障碍物在远处，如果自车采用激进换道的模式，车辆也会在较短时间和距离内完成换道操作，这同自车距离障碍物较近时为避障进行换道情形是一致的，所以可采用减小障碍物与自车距离的方法，得到一定换道时间所对应冲击度的合理约束范围。取平均换道时间为6s，标准差为1.2s，将换道模式分为激进型、普通型和保守型，若换道时间在4.8s以内认为属激进型，（4.8～7.2）s之间完成换道操作属普通型，换道操作时间在7.2s以上属舒适型换道模式，根据表1计算结果，给出了不同换道模式下冲击度约束条件，如表2所示。

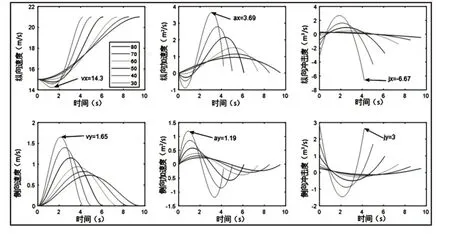
图4 不同障碍距离自车速度、加速度和冲击度曲线Fig.4 Self Vehicle’s Velocity、Acceleration and Jerking of Different Obstacle Distances

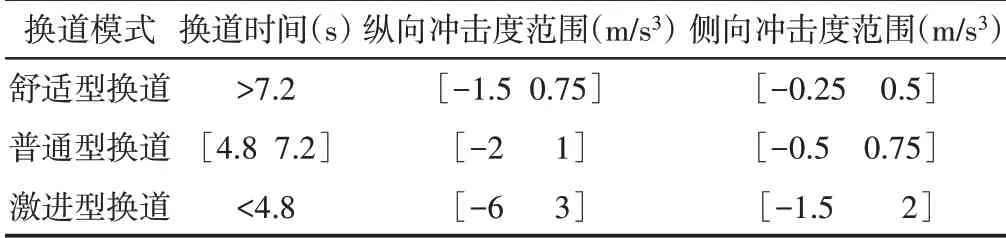
表2 不同换道模式下的冲击度Tab.2 Jerkings in Different Lane-Change Modes

在自车与前方障碍车相距80m时，选择不同换道模式，即通过改变侧向和纵向冲击度约束大小，可得到激进型、普通型和舒适型换道的换道时间分别为4.7s、6.69s和9.96s。激进型换道模式下，自车S与目标车道前车PA、后车FA的运动轨迹图，如图5所示。十字符号线为目标车道前车PA的运动轨迹，o形符号线为后车FA的运动轨迹，星号线为自车轨迹，可见采用激进模式，换道时间最短，纵向位移距离为79.02m，能快速成功完成换道。

图5 自车与目标车道车辆PA、FA运动轨迹Fig.5 Motion Trajectories of Self Vehicle、PA and FA

5 结论

设计了可避让前方障碍车且能成功插入相邻车道两车之间的动态换道优化轨迹；分析了换道时间与冲击度约束的关系，将换道分为激进型、普通型和保守型，给出了不同换道模式下汽车冲击度约束的合理范围。下一步将探索模型预测等方法，以实现更复杂场景的换道轨迹优化和轨迹跟踪。