考虑属性组合关联的机械产品属性约简方法

王立业，萨日娜，2，，张利春

（1.内蒙古工业大学机械工程学院，内蒙古 呼和浩特 010051；2.浙江大学机械工程学院，浙江 杭州 310027；3.康力电梯股份有限公司，江苏 苏州 215213）

1 引言

近年来，机械产品的属性识别工作对产品设计能够起到减少工作量加快工作效率的意义，能够从原始数据中剔除掉冗余信息，保留核心内容。在产品的属性识别方面国内外学者做了一些研究，主要分为两个方面：一方面是根据专家的经验来对产品进行归纳和分析，这种方法针对一些型号较少的特定机械产品。文献［1］提出一种集成约束模糊随机层次分析法，克服了层次分析法局限性；文献［2］研究了运用层次分析法和偏好排序组织法的决策方法进行属性识别，克服了在决策过程中需要考虑大量的标准的局限性。另一方面越来越多的学者利用数据挖掘技术从设备实例数据库中进行分析对产品属性进行约简提取核心属性。主要有文献［3］利用正域的概念提出了一种属性依赖度的计算方法，与传统方法比较精度得到了提高；文献［4］提出了以正域来表示属性重要度的约简算法，将重要度大的属性逐步加入到约简属性集中，直至满足预定义的停止条件。以上研究都是基于正域来进行属性重要度计算从而筛选出核心属性，利用正域计算时是以正区域基数与几何基数之比计算出属性重要度，有时不能很好的区分属性之间的相关性从而导致最终约简存在冗余。

因此，考虑属性组合对条件属性的关联性，利用评估实验室（Decision—Making and Trial Evaluation Laboratory，DEMATEL）方法得出条件属性权重，并结合正域依赖度计算出约简属性组合重要度；考虑到属性组合对决策属性的关联性，利用互信息计算属性组合相关度。在此基础上建立机械产品属性约简多目标0-1规划数学模型。提出改进多目标布谷鸟算法得出机械产品属性约简Pareto前沿，利用区间犹豫模糊集对属性约简集Pareto前沿优选，最终确定出机械产品属性约简最优方案。

2 考虑属性组合关联的多目标属性约简模型

机械产品属性集合为Xm=｛x1，x2，…，xm｝，式中：xi—某个属性，i=1，…，m，需要从m个属性中筛选出n个属性代表全部的m个属性，其中，n＜m，选取的n个属性在进行相关设计工作时要达到与用m个属性基本相同的效果。

首先根据粗糙集理论［5］建立产品属性的信息表达系统S=（U，A，V，f），式中：U—论域，代表各个属性属性的数值集合；A—产品的所有属性；V—各个属性的取值范围；f—信息函数。

假设属性子集P⊂A，xi，xj∈U，定义二元关系IND（P）成为等价关系：IND(P)={(xi，xj)∈U×U|∀p∈P，p(xi)=p(xj)}称xi，xj在S中关于属性集p是等价的，当且仅当p（x）i=p（x）j对所有的p∈P成立，即xi，xj不能用P中的属性加以区别。由此可以区别出属性的辨别能力大小。

在机械产品信息系统S=（U，A，V，f）中，设X⊂U是个体全域上的子集，设P⊆A是属性域的子集，则X的上近似集和下近似集分别为：

上下近似集将论域U划分为三个区域：正域POSp(X)=、边界域Bndp(X)=-和负域NEGp(X)=U-。

2.1 考虑条件属性关联的属性组合重要度

利用正域进行属性重要度计算时对原始数据的依赖性大，一旦数据出现错误直接导致计算结果产生偏差。因此首先通过基于正域的属性约简计算出各个属性的初始重要度再结合DEMATEL方法［6］计算出属性的权重，得出最终属性重要度，保证结果的可靠性。

基于正域的条件属性c对于决策属性D的重要度如下式所示：

利用DEMATEL方法计算属性权重时，首先建立属性的影响矩阵B：

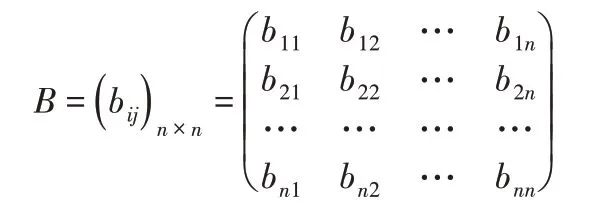
式中：bij—属性i对属性j的影响程度，影响程度取四个等级，0时没有影响；1—较小；2—有影响；3—影响较大。

将影响矩阵B归一化处理得到M=(mij)n×n=B M，其中，m=

根据M计算得出综合影响矩阵X=(xij)n×n=M(I-X)-1式中：（I-X）-1—I-X的 逆矩阵；I—单位矩阵。

根据X计算出各条件属性的中心度与原因度如下：

最终确定出权重大小如下式所示：

在基于正域的属性约简中加入DEMATEL方法确定权重最终得出机械产品条件属性子集A对于决策属性D的重要度如下式所示：

2.2 考虑决策属性关联的属性组合相关度

利用式（1）正区域基数与集合基数之比计算出的属性重要度有时不能很好的区分机械产品属性之间的相关性从而导致最终约简结果存在冗余，这种方法有着一定的局限性，因此引入互信息理论［7］来描述两个属性之间的相关性大小，通过限定条件属性之间的互信息值的大小来提高属性组合的分辨度进一步约简属性。

如机械产品信息系统表示为S=（U，Ai，V，f），则属性子集A的信息熵为：

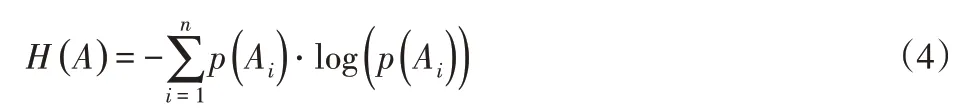
属性子集A相对于属性子集B的条件信息熵为：

属性ɑ在属性子集B的条件下与决策属性的条件熵为：

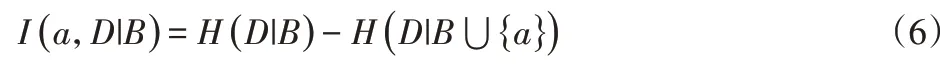
属性组合A互信息计算步骤：

（1）计算属性组合中属性子集B与决策属性之间的互信息值I（B，D），开始时B中只包含属性组合中第一个属性，i+1。

（2）计算属性组合中第i个属性在已有属性子集的条件下与决策属性之间的互信息I（Ai，D|B）。

（3）计算属性子集B与决策属性之间的互信息值I（ɑ，D|B）+I（B，D）=Inew（B，D），其中Inew（B，D）表示更新后的I（B，D）。

（4）如果B≠A，进入第一步；如果B=A，结束并输出I（A，D）。

根据这里内容多目标属性约简数学模型可以表示为：

属性约简模型总体思路，如图1所示。

图1 属性约简模型总体思路Fig.1 General Idea of Attribute Reduction Model

3 属性约简算法

3.1 改进多目标布谷鸟算法

机械产品属性约简问题可以看作是一个以不同关键属性组合方式为变量，把条件属性组合的重要度和属性组合的相关度为目标的0-1优化问题。

根据传统的布谷鸟算法建立多目标布谷鸟算法［8］，将布谷鸟的产卵行为进行三个理想状态的假设：

（1）布谷鸟一次产2个蛋，代表两个建立的目标，并随机选择鸟巢来孵化它。

（2）在随机选择的一组鸟巢中，最优的鸟巢保留给下一代。

（3）可选择的寄生巢的数量是固定的，寄生巢主人发现外来鸟蛋的概率为pɑ，其中0≤pɑ≤1。

3.1.1 鸟巢编码方式

假设有n=6个鸟巢，鸟巢位置定义为n维坐标X=｛x1，x2，…，x6｝，在鸟巢位置选取时，采0-1编码方式，0表示未选中该鸟巢，1表示选中该鸟巢。

3.1.2 鸟巢更新策略

在n维空间中，第i个鸟巢位置向量为Xi=［xi1，xi2，…，xin］。原有鸟巢初始化采用随机初始化，但是这种初始化不能在空间中得到均有的鸟巢位置，这也就导致在迭代过程中不能尽快的收敛，所以在这里采用sobol［9］序列初始化方法，能够得到更为均匀的鸟巢位置更快的搜索到Pareto解。

图2 两种初始化对比Fig.2 Two Initialization Comparisons

布谷鸟算法的位置更新机制是采用莱维飞行更新机制，依赖随机步长，这种更新机制虽然能够保证算法最终避免陷入局部最优，但是也会导致收敛速度降低。在前期搜索阶段，大步长搜索，以便找到全局最优解；在算法后期的搜索阶段，小步长在最优位置附近搜索，从而提高算法的收敛速度。如式（8）所示步长与迭代次数成反比，随迭代次数的增多步长越小，从而逐渐缩小搜索范围。

为了能够使得鸟巢位置向最优位置进行快速靠近，因此把遗传算法的交叉［10］操作引入到位置更新机制当中，将产生的新的鸟巢Xi（t+1）’与当前最优鸟巢Xit以Pc的概率进行交叉操作得到新的鸟巢位置Xit+1，如下所示。

图3 鸟巢交叉操作Fig.3 Bird’s Nest Crossover Operation

3.2 基于区间犹豫模糊集的属性约简方案优选

假设根据算法得出ɑ组Pareto解集，每组Pareto解集中属性个数为b。利用区间犹豫模糊集多属性群决策方法［11-12］来对Pareto解集中的方案进行评价选出最终方案。

评价值在此选用语言术语（不重要、比较重要、重要、很重要）进行评价，转换为区间分别为［0，1］、［1，2］、［2，3］、［3，4］。定义决策者Pk（k=1，2，…，5）对于方案ci（i=1，2，…，ɑ）的属性xj（j=1，2，…，6）通过区间犹豫模糊集表示，其中为评价值。

在此选用五位专家作为决策者及根据专家权威值人为给定权重ωk=（ω1，ω2，ω3，ω4，ω5）。

集结决策矩阵以及专家权重信息进行方案评价，第i个方案的评价值为：

最终选取评价值最高的Pareto解作为最终方案。

算法主要步骤如下：

输入.决策矩阵。

输出.Pareto解集。

（1）设置基本属性迭代次数1000、种群个数15、交叉概率0.5、淘汰概率0.1、并输入模型。

（2）产生初始种群X，并计算目标函数值F1、F2。

（3）判断是否达到最大迭代次数，如果是转到（9）。

（4）根据Pareto支配策略挑选非支配集，产生新种群X1。

（5）计算淘汰概率，如大于0.1淘汰种群并产生新种群，如小于0.1进入下一步。

（6）合并X1、X2，由Pareto支配策略产生非支配解存入外部档案。

（7）计算交叉概率，如＞0.5与父代交叉产生新种群，如＜0.5进入（9）。

（8）合并X2、X3，由Pareto支配策略产生非支配解存入外部档案.

（9）输出Pareto最优解集。

基于改进的多目标布谷鸟算法详细流程图，如图4所示。

图4 算法流程图Fig.4 Algorithm Flow Chart

4 实例分析

以住宅电梯产品属性集合X=｛x1，x2，…，x17｝为例进行分析，x1，x2，…，x17依次表示为电梯属性额定载重、可乘人数、电梯速度、轿厢宽、轿厢深、轿厢高、轿门和层门宽、轿门和层门高、轿门和层门型式、井道宽、井道深、底坑深度、顶层高度、机房面积、机房宽、机房深、机房高度共17个，其中轿门和层门型式有旁开门和中分门，在住宅电梯信息决策表中分别用0和1表示。以x1，x2，x3为决策属性，其余属性为条件属性建立电梯属性信息表达系统，将电梯的17个属性列入到属性集合X中，得到17×200的原始决策表，如表2所示。

表2 住宅电梯属性信息决策表Tab.2 Decision Table of Residential Elevator Property Information

以NSGA_II算法作为比较算法，设定NSGA_II算法种群大小为100，最大迭代次数为1000，交叉概率为0.9，变异概率为0.1。仿真环境为Intel（R）Core（TM）i7-8550U，CPU@1.80GHz，RAM 8GB，系统Windows 10，仿真平台Matlab2016a。仿真结果，如图5所示。各目标变化曲线，如图6所示。

由表3可以看出改进布谷鸟算法比NSGA_II算法平均求解时间耗时少，算法效率更高，得到的Pareto前沿解集拥挤距离更大，解集在目标空间分布更加均匀，并且得到的平均非支配解集的个数更多，可以看出改进布谷鸟算法较优。

表3 仿真结果对比Tab.3 Comparison of Simulation Results

属性组合的平均重要度和相关度的变化曲线，如图5（a）、图5（b）所示。从图6可以看出，这里改进算法在经过100次迭代后就逐渐趋于稳定；NSGA_II算法则是近300次迭代后才趋于稳定。虽然NSGA_II算法在前期迭代过程中收敛速度较快，但从整体看改进布谷鸟算法的各个目标函数变化曲线的收敛速度要快于NSGA_II算法，改进布谷鸟算法有明显优势。

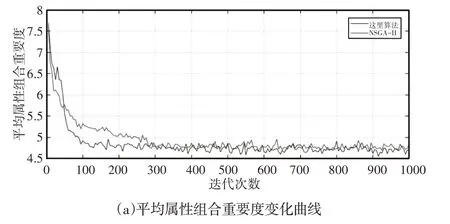
图5 迭代过程目标函数的变化趋势Fig.5 The Variation Trend of the Iterative Process Objective Function

迭代1000次时利用NSGA_II算法与改进布谷鸟算法求解的Pareto解集对比图，如图6所示。其中改进布谷鸟算法根据Pareto支配原则得出了26个Pareto前沿解集。这26个点都是支配解，都可作为最终的解。从图7中可以看出改进布谷鸟算法相比NSGA_II算法得出的Pareto前沿更优，更适合求解多目标属性约简问题。

图6 电梯属性约简Pareto前沿Fig.6 Elevator Property Reduces Pareto Cutting Edge

对于得出的26组Pareto解集，利用区间犹豫模糊集多属性群决策方法来对Pareto解集中的方案进行评价。

在此选用五位专家作为决策者及根据专家权威值人为给定权重ωk=（ω1，ω2，ω3，ω4，ω5），如表4所示。

表4 专家权重Tab.4 Expert Weight

最终得到方案集的评价值，如图7所示。选出最优方案c11，如表5所示。

图7 26组方案评价值Fig.7 26 Groups of Scheme Evaluation Value

表5 约简后属性Tab.5 Reduced Attribute

基于正域的属性约简算法得出的约简结果，约简后属性个数为8个，多于所提方法的6个，如表6所示。这里算法得出的属性也都属于基于正域得出的属性并且剔除了其中的两个属性，说明这里算法约简结果具有更少的冗余。进一步分析两种算法约简后属性，基于正域的约简算法比这里所提算法多出的两个属性为可乘人数和机房深，可乘人数与额定载重相关性较强，而机房深相对于机房面积并没有太重要。以上分析可以看出文中所提方法约简效果更优，对于属性关联性较大的机械产品的属性约简效果较好。

表6 基于正域算法约简后属性Tab6 Attribute Reduction Based on Positive Domain Algorithm

5 结束语

针对机械产品属性之间存在关联性的问题，提出了考虑属性组合关联的机械产品属性约简方法。（1）考虑约简属性组合对条件属性的关联性，利用DEMATEL方法结合正域依赖度计算方法得出约简属性组合重要度；考虑约简属性组合对决策属性的关联性，利用互信息理论计算约简属性组合的相关度。弥补了传统正域约简的局限性。（2）建立机械产品属性约简多目标（0～1）规划数学模型并提出改进多目标布谷鸟算法，与NSGA_II算法对比收敛更快，解的分布更加均匀。（3）借助区间犹豫模糊集，对属性约简集Pareto前沿优选，确定机械产品属性约简最优方案。最终以住宅电梯产品属性约简为例，验证了所提方法的有效性和可行性。