基于隐式参数化设计的车身焊点布局优化研究
2022-02-23武振江杨建森
武振江,杨建森,曹 建,吴 杨
(中汽研(天津)汽车工程研究院有限公司第三开发本部,天津 300300)
1 引言
随着汽车国六排放标准的提出,汽车轻量化技术面临着巨大挑战[1-3]。多材料、变截面等新型设计手段被大量应用,这对传统焊点工艺带来重要影响。铝合金等新型材料的引入,使得焊接时的热输入量提高二到四倍,大大增加了焊接成本。同时,焊点分布不均也会导致结构强度的不足与工艺成本的增加。因此,基于新技术车辆,在平衡制造成本与汽车性能的前提下,如何实现焊点的优化布局具有重要意义。
近几年,国内外学者针对焊点布局方面开展了大量研究。文献[4]通过对商用车驾驶室进行焊点布局优化,在焊点数量不增加的前提下,使得车身刚度得到提升。文献[5]基于均匀循环理论,对车身关键接头位置进行焊点优化布局,保证扭转刚度的前提下,使得焊点数量减少26%。文献[6]采用变密度拓扑优化的方法对焊点单元密度进行优化,优化结果不仅降低了焊点数量,同时使得一阶固有频率提升1.28Hz,有效改善共振现象。文献[7]通过建立“质量-能耗”模型,优化焊点工艺参数,降低焊接过程中的能量消耗。文献[8]通过对叠层焊点的随机振动以及可靠性分析,建立了焊点直径与疲劳寿命的关系模型。文献[9]提出一种优化决策方法实现焊点参数的改变,并通过鲁棒性分析建立焊点个数对结构性能的影响关系,兼顾工艺成本与汽车性能的前提下,降低焊点数量。文献[10]通过对焊点布局以及板件搭接长度的优化,进一步改善疲劳寿命。文献[11]通过对车门异响进行仿真分析,获取主要异响区域,并采用拓扑优化方法对车门结构的焊点布置进行优化设计,使得车门异响问题得到有效解决。文献[12]研究了两种焊点模式下的太阳能清洁车的车架结构强度,证实了焊点形式对强度的影响很大,对焊点参数优化进一步提高结构性能。文献[13]对电动汽车电池包的焊点布局进行优化研究,采用变密度法拓扑优化的方法,实现焊点数量的减少,并利用随机振动来对优化结果的合理性进行验证。
大量文献已证实了焊点布局对车身轻量化设计的重要性,然而,针对于研究方法的准确性与计算效率还有待提高,如文献5中采用降低焊点弹性模量的方法来等效迭代过程中不同焊点方案有限元模型的重建,使得效率得到很大提升,准确性会有一定程度的降低。基于此,以某款SUV车型为研究对象,采用隐式参数化设计方法,实现焊点模型自动化更新,通过对车身关键区域焊点间距的优化设计,在保证结构性能的前提下,对焊点重新布局,以实现轻量化设计与降低工艺成本的目的。
2 隐式参数化设计原理
与显示参数化设计不同,隐式参数化的几何模型中通过映射的模式将各零部件连接在一起[14]。这种映射连接的本质是建立几何之间的拓扑关系,使得在进行设计参数的修改时,不影响原有模型的连接关系,实现自适应改变,在设计流程上展示了基于SFE CONCEPT软件的隐式参数化设计方法与传统设计流程的对比,如图1所示。
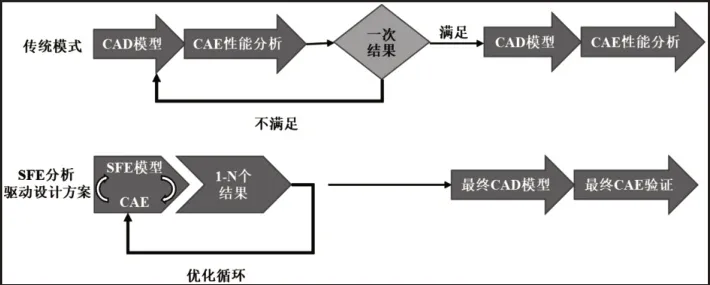
图1 基于SFE CONCEPT的设计流程与传统方式的对比Fig.1 Comparison Between the Design Process Based on SFE Concept and the Traditional
具体操作步骤如下:
(1)将有限元网格模型导入SFE CONCEPT软件中,建立各零部件的参数化模型,将材料属性与尺寸属性赋予参数化部件,并确定各零部件间的映射关系。
(2)利用map技术建立部件间的拓扑位置关系,并采用多层翻边技术建立连接部分的工艺形式,如焊接、胶粘等,并设置相应的工艺参数。
(3)利用SFE CONCEPT内置的网格自动划分功能,生成用于参数化设计的有限元模型。
隐式参数化建模的原理图,如图2所示。设计工程师只需在Isight优化平台上集成参数化模型以及相关计算模块,定义设计变量以及样本空间,然后设定优化的目标值和约束条件。完成上述步骤,SFE CONCEPT就可以实现自动化的循环优化过程,既保证了模型更新的准确性,同时大大的降低了人为的操作时间和精力。

图2 隐式参数化建模的原理图Fig.2 Schematic Diagram of Implicit Parametric Modeling
3 性能指标的确定
焊点的布置不仅与制造成本有关,而且对整个结构的刚度、强度和NVH等性能也有着重要的影响,因此以某款SUV车型为研究对象,通过对参数化设计前的白车身模型进行弯扭工况的仿真分析,获得原始模型的性能参数,从而确定约束条件,并用来验证参数化模型的准确性,相关验证结果,如图3~图6所示。其中BIW-SFE为基于隐式参数化设计的白车身模型,BIW-CAE为前期对标车型白车身有限元模型。通过仿真计算,测得原车型以及SFE CONCEPT建立的参数化模型的弯扭刚度、模态的结果以及质量与焊点个数的统计,其测量值与原始模型的对比误差,如表1所示。
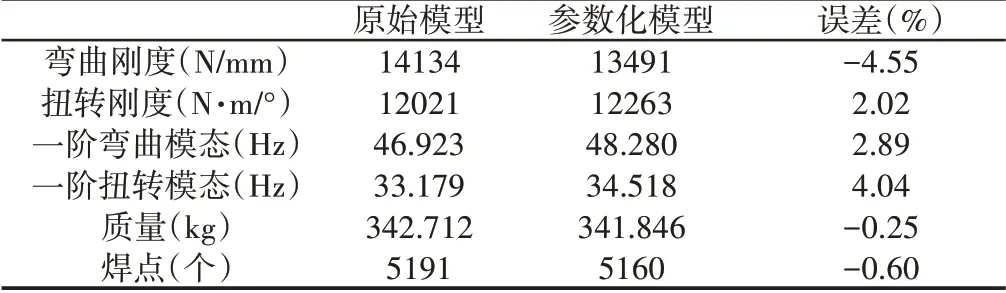
表1 基本性能对比Tab.1 Basic Performance Comparison

图3 扭转刚度结果Fig.3 Torsional Stiffness Results
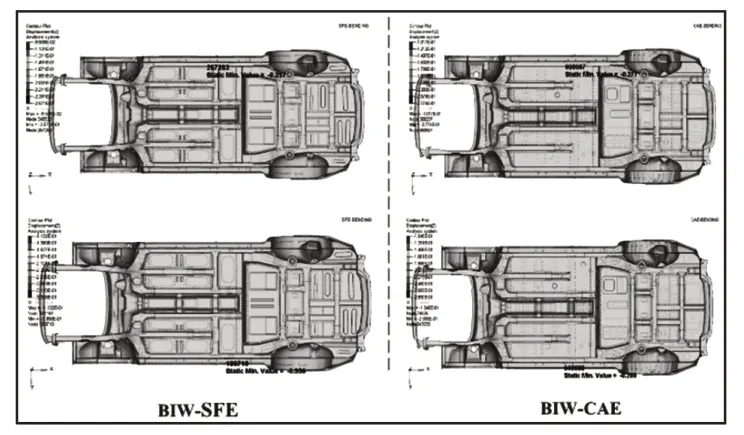
图4 弯曲刚度结果Fig.4 Bending Stiffness Results
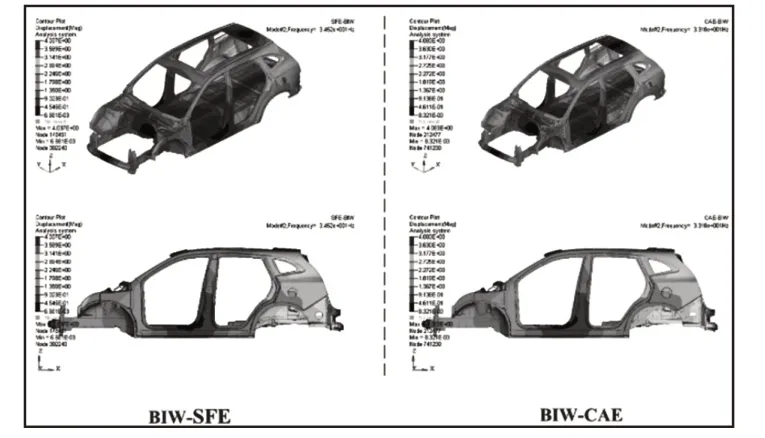
图5 一阶扭转模态结果Fig.5 First Order Torsional Modal Results
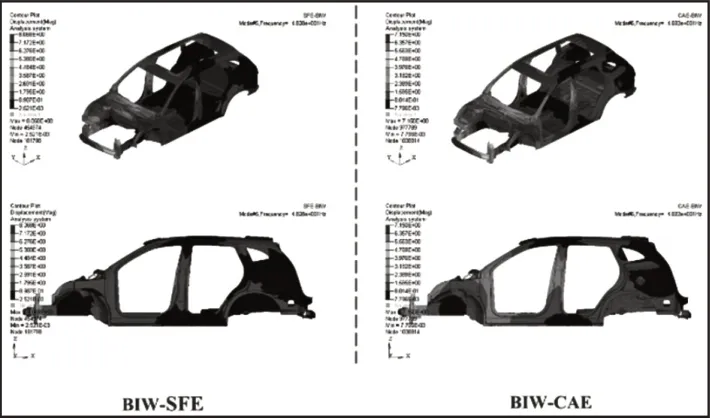
图6 一阶弯曲模态结果Fig.6 First Order Bending Modal Results
对比表1中的性能误差,均在5%以内,因此证明参数化模型的精度是可靠的。基于平台开发考虑,以下车体为研究对象,通过改变下车体地板上关键零部件连接部位的焊点间距信息,在保证扭转刚度的前提下,对焊点优化布局。建立优化设计的数学模型如下:
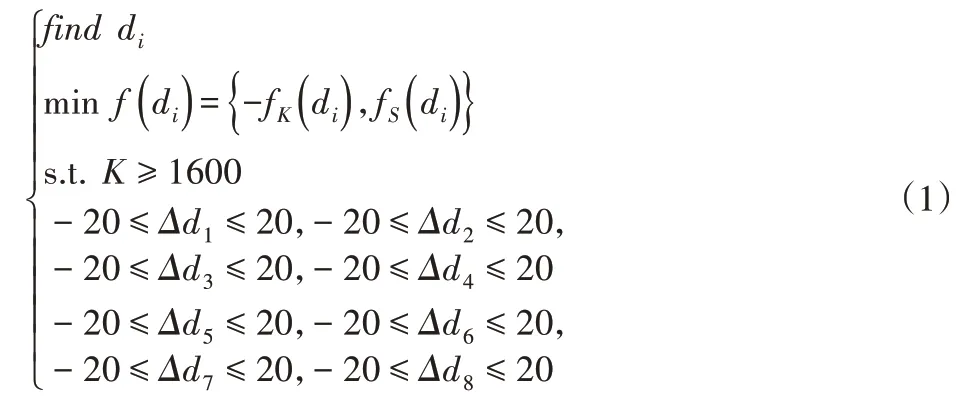
式中:Δdi—选取位置的焊点间距变化量,选取8处连接区域,因此i=1~8。扭转刚度K与焊点个数分别是关于焊点间距变化量的函数。通过仿真计算下车体平台的扭转刚度为1766N·m/°,通过对一系列对标车型的分析,将1600N·m/°定为优化过程中的性能约束。
4 试验设计
设计空间中的采样点是建立代理模型的基础。许多不同的试验设计方法可用于样本空间的确定,如最优拉丁超立方体设计、全因子设计以及中心组合设计等。由于最优拉丁超立方体设计方法具有空间均匀性与投影均匀性的优势,因此基于后期函数拟合的准确性以及计算效率的考虑,采用该方法获得80组试验样本点,表2中展示了部分样本点数据。
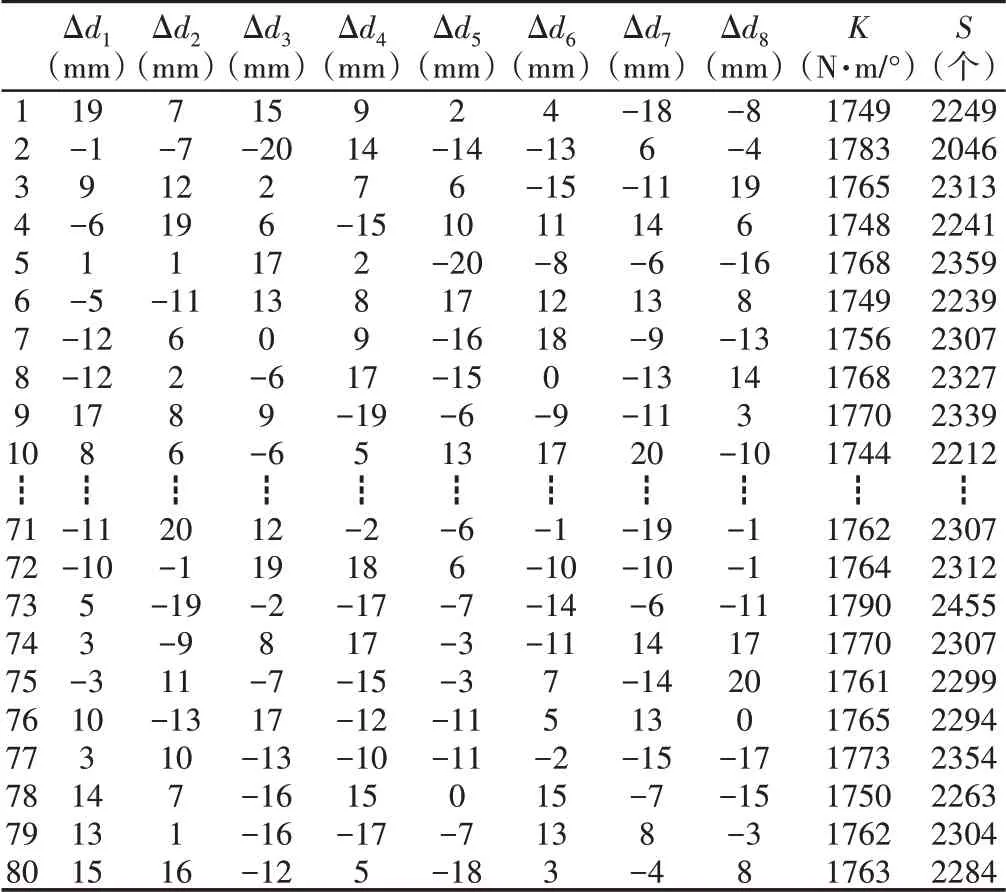
表2 试验设计与结果Tab.2 Fractional Factorial Design and Results
5 响应面模型分析
由于优化过程中迭代次数较多,采用数值分析方法求解目标函数值时,计算量太大。为了提高计算效率,通常采用近似模型来逼近目标函数,如响应面模型、径向基函数、支持向量回归模型等。本研究采用响应面法,具有效率高、准确度好的优点。
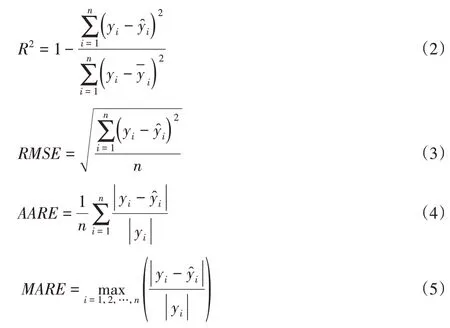
式中:R2—方差系数;RMSE—均方根误差;AARE—平均绝对相对误差;MARE—最大绝对相对误差。
通过80组样本点,分别建立了扭转刚度、焊点个数与焊点间距变化量的响应面模型如下:
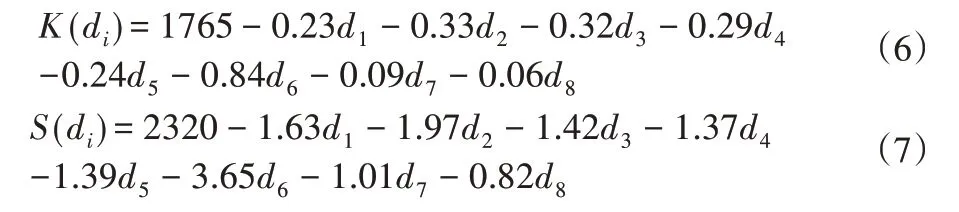
式中:K(di)—扭转刚度;S(di)—焊点个数;di—第i个焊点连接区域,i=1~8。
代理模型误差分析,如表3所示。一般来说,R2越接近于1,MARE、AARE和RMSE的值越接近于0表示拟合效果越好。由此可以看出,两组响应面模型的拟合效果较好,可以保证后续优化结果的准确性和有效性。

表3 代理模型误差分析Tab.3 Error Analysis of Agent Model
6 优化结果
经多次迭代,提取优化结果,部分优化结果,如表4所示。基于不同的实际要求,可从优化结果中进行方案选择,同时也可以结合权重系数以及决策方法进行择优选取。基于轻量化以及制造成本的考虑,选取了优化方案中焊点个数最少的方案进行对比,优化前后的结果对比,如表5所示。
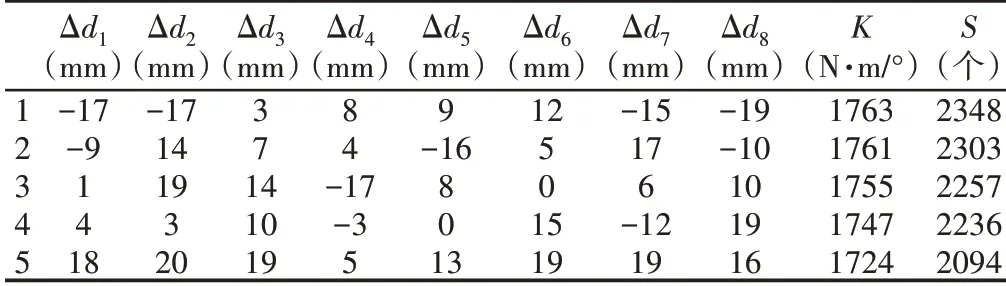
表4 部分优化结果Tab.4 Partial Optimization Results
通过表5可以观察到,扭转刚度基本没有变化,焊点个数减少179个,效果较为明显,预计在整车级别上,将会有更大的成本优势,同时也验证了该上述方法的高效性与实用性。

表5 优化前后结果对比Tab.5 Comparison of Results Before and After Optimization
7 结论
基于平台开发设计,对某基础车型的焊点进行优化布局。首先对其有限元模型进行了建立和分析,得到初始状态的性能及优化区域焊点数量;其次,基于隐式参数化设计方法建立参数化模型,在Isight优化平台集成相关计算模块进行了焊点布局优化;最后将优化前后的性能及焊点数量进行了对比分析。在扭转刚度基本不变的前提下,焊点总数量减少179个,优化效果明显。这里在对焊点布置进行优化时只关注了扭转工况下的刚度,验证隐式参数化设计结合Isight优化平台方法在汽车平台开发设计方面的高效性与实用性,存在一定的局限性,在今后的研究中会综合考虑多种性能,以便得到更加合理的焊点布置方案。
