简谐运动特征及其分类应用

罗倩敏(正高级教师) 李亮芝

（北京市第十八中学）

简谐运动是一种速度和加速度都不断变化的“双变”运动，是振动中最简单、最基本的一种运动形式.简谐运动在简谐波、重力场、电场、磁场、分子力场中多有体现，因此，研究简谐运动特征及其分类应用十分必要.

1 简谐运动的特征

1.1 回复力特征

图1所示为弹簧振子.设轻弹簧的劲度系数为k，小球质量为m，O为平衡位置，不计摩擦与空气阻力，弹簧弹力提供回复力，定义水平向右为正方向，当位移为x时，得简谐运动回复力F＝－kx.

图1

1.2 动力学特征

由牛顿第二定律F＝ma，联立回复力F＝－kx，得

1.3 振动特征

以第一次位于平衡位置时刻为计时起点，用传感器得小球的位移x(或速度v、加速度a)随时间t呈正弦(或余弦)函数变化，即振动方程x＝Asin(ωt＋φ0)，v＝ωAcos(ωt＋φ0)，a＝－ω2Asin(ωt＋φ0).

1.4 速度—位移特征

设小球在O点的速度为v0，在任意点的速度为v，两点间位移为x，由于回复力是线性变化的，所以在这段位移内的平均回复力为，由动能定理得

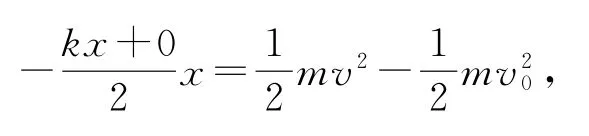
1.5 对称特征

根据简谐运动的特征，不难发现位移、速度和加速度关于平衡位置对称.

2 简谐运动分类应用

2.1 简谐波

例1一列简谐横波某时刻波形如图2所示.由该时刻开始计时，质点L的振动情况如图3所示.下列说法正确的是( ).

图2

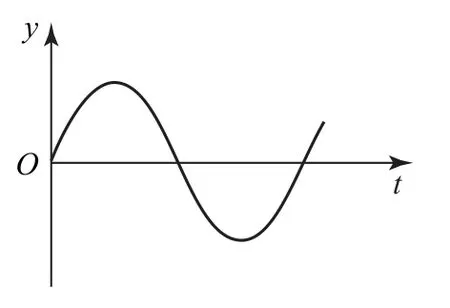
图3

A.该横波沿x轴正方向传播，且质点N在该时刻向y轴负方向运动

B.质点L经半个周期将沿x轴正方向移动到N点

C.该时刻质点K与M的速度、加速度都相同

D.设质点L的质量为m，最大速率为v，质点从该时刻起经过半个周期的奇数倍时间内其动量变化为－2mv

解析

由图3可知，质点L在该时刻向y轴正方向运动，依据“同侧”(即质点振动方向与波传播方向处在波的图像的同侧)法，由图2可知，该横波沿x轴正方向传播.同理可知，质点N在该时刻向y轴负方向运动.由于波传播的是振动形式，质点并不随波一起迁移，所以选项A正确，选项B错误.因K、M间隔半个波长，则K、M的振动步调始终相反，因此，该时刻质点K与M的速度、加速度大小相同，但加速度方向不同，选项C错误；质点L从该时刻起经过半个周期的奇数倍时间，质点的初末位置均在平衡位置，且振动方向相反，其动量变化为－2mv，故选项D正确.

点评

简谐波是简谐运动在空间传递时形成的波动，其波函数为正弦或余弦函数形式.解决这类问题要关注以下几点：1)明确各质点的振动频率、波长、波速，以及它们之间的关系.2)掌握“同侧”法判断质点的振动方向和波的传播方向的关系，知道质点不会随波迁移，理解波动图像与振动图像的区别与关联，注意位移、速度(动量)和加速度都是矢量，明白其变化的周期性和对称性.

2.2 重力场

例2如图4所示，有摆长为l的单摆，摆球质量为m，将小球拉开偏离竖直线微小角度θ(θ＜5°)由静止释放，不计空气阻力，取重力加速度为g.

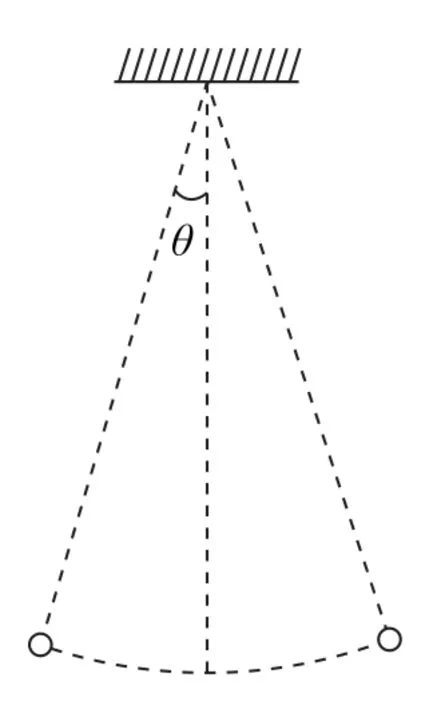
图4

(1)试证明小球做简谐运动；

解析

(1)如图5所示，设小球运动到偏离竖直线α(α＜θ)角时，对应平衡位置O的位移为x，显然重力沿运动轨迹切向的分力提供回复力，即F＝mgsinα，由于θ＜5°，由几何关系得联立解得因F指向平衡位置O，而x背向平衡位置O，即F＝故小球是做简谐运动.

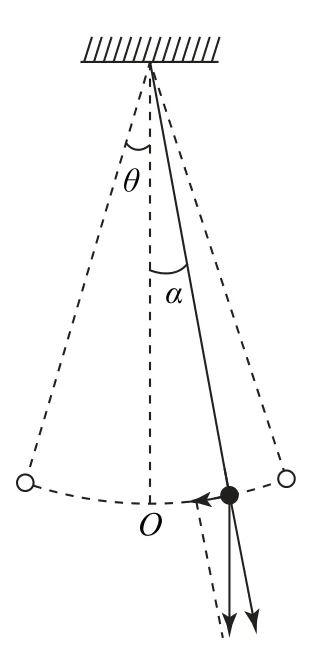
图5

点评

重力场中的简谐运动主要有单摆与弹簧振子两种模型.解决这类问题的关键，一是确定平衡位置所在点)二是找到提供回复力的力，可以是某力的分力，也可以是合力)三是明确条件(最大摆角小于5°或在弹性限度内)，从而根据简谐运动的动能定理、特征方程、几何关系等规律解决相关问题.

2.3 电场

例3如图6所示，一个半径为R、电荷量为＋Q的均匀带电圆环固定在真空中，环心为O，MN是其中轴线.现让一电荷量为－q、质量为m的带电粒子从MN上的P点由静止释放，P、O间的距离为d(d≪R)，不计粒子重力.求：

图6

(1)带电粒子运动的周期T；

(2)粒子运动到距离O点为x0时的速度大小v.

解析

(1)设带电环上微元长Δl，其带电荷量为由场强公式得如图7所示，而整理得E＝因x≪R，简化得，方向由O指向P.带电粒子所受电场力为F＝Eq，即

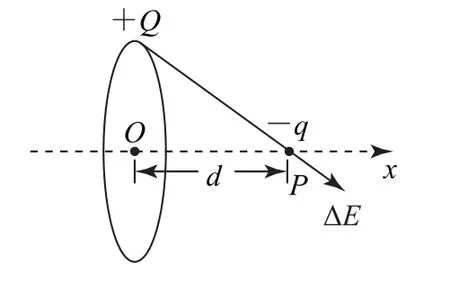
图7

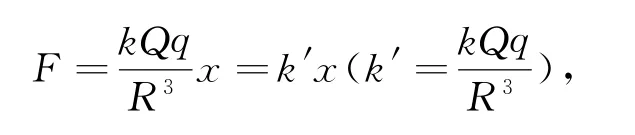
方向指向O，即带电粒子做简谐运动，由简谐运动周期公式得

(2)对－q，从P点到x0处由动能定理得解得

点评

电场中的简谐运动，因电场有匀强和非匀强之分，所以在匀强电场中有类单摆和类弹簧振子模型，在非匀强电场中有均匀带电圆环形中轴线电场和等量同种电荷的连线中垂线的电场两种模型.解决这类问题的关键，一是找到场强为零的点——平衡位置)二是由微元法、对称法、等效法等找回复力)三是明确模型条件，从而由简谐运动的特征方程、动能定理、几何关系等规律解决相关问题.

2.4 磁场

例4如图8所示，光滑的平行金属导轨水平放置，导轨间距为L，左端接一阻值为R的定值电阻；导轨处在磁感应强度为B的匀强磁场中，磁场方向与导轨平面垂直.一根与导轨垂直的铜棒在与导轨平行且共面的外力作用下，在导轨上做振幅为A的简谐运动，振动周期为T.已知铜棒电阻为r，电子电荷量为e.导轨的电阻不计，设计时起点为平衡位置且向左运动，位移向左为负，电流顺时针为正方向.

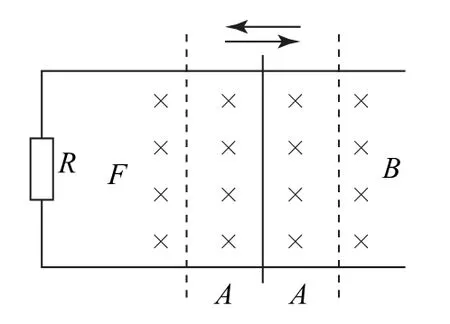
图8

(1)在图9中画出通过电阻R的电流i随时间t变化的图像；

图9

(2)求在一个周期T内，电阻R产生的焦耳热；

(3)从微观角度，求出铜棒内一个电子所受金属离子撞击的平均阻力的最大值；

(4)在同一坐标系中大致画出铜棒受回复力、安培力、外力相对平衡位置位移x的图像.

解析

(1)因铜棒做简谐运动，以平衡位置为计时起点，其感应电动势为E＝BLvmcosωt，由欧姆定律得联立得i＝其图像如图10所示.

图10

(2)一个周期T内，电阻R产生的焦耳热为Q＝

(3)任何时刻电子均认为受力平衡，即有evB－由闭合电路欧姆定律有BLv＝ir＋U，联立解得显然当电流最大时，电子所受金属离子撞击的平均阻力最大，即

(4)由于铜棒做简谐运动，则其回复力满足F外＝－kx，由初始状态得知图像是在第二、四象限的直线.由于铜棒受安培力FB＝BiL，联立由已知得铜棒的最大速度是一定的，则铜棒的速度与位移关系满足方程，即v-x成椭圆规律变化，而FB∝v，则FB∝x，即FB-x也成椭圆规律变化，由于安培力与外力是共线的，则得F外-x呈抛物线变化，故其对应图像如图11所示.

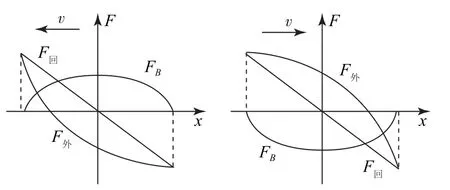
图11

点评

匀强磁场中的简谐运动，主要有类单摆和类弹簧振子两种模型.解决这类问题的关键，一是明确带电粒子做简谐运动时，洛伦兹力不提供回复力)二是知道导体棒做简谐运动时，因电流有恒定与振荡变化之分，应区别对待.若是恒定电流，则将安培力和重力、匀强电场力一样去分析，找到回复力)若是振荡变化电流，则要根据简谐运动物理量间的函数关系进行数理处理或物理矢量合成，如由回复力—位移关系(线性)、速度—位移关系(椭圆)、力的合成，推导出外力—位移关系为抛物线)三是要运用力电综合知识、宏观微观关联等解决问题.

2.5 叠加场

例5有一摆长为l的绝缘单摆，摆球质量为m、带电荷量为＋q，处在正交且匀强的电磁场中，静止时绝缘线偏离竖直方向夹角α＝37°，如图12所示.用绝缘手套将小球拉开使之偏离平衡位置微小角度θ(θ＜5°)静止释放，小球围绕平衡位置小幅振动，不计空气阻力，重力加速度为g.试求：

图12

(1)匀强电场场强E的大小及小球运动的周期T.

(2)小球的最大速度vm及绝缘线对小球的最大拉力Fm.

解析

(1)小球静止时受力平衡，有Eq＝mgtan37°，即小球振动是由电场力与重力的合力沿轨迹切向指向平衡位置的分力提供，洛伦兹力始终与速度方向垂直，即同例2方法可得

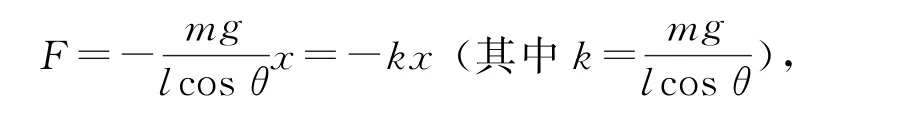
故小球做简谐运动，则其运动周期

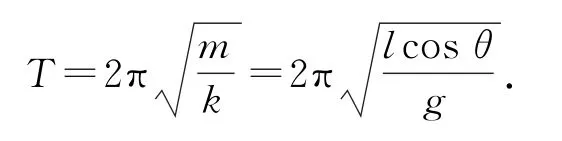
(2)对小球，显然在平衡位置速度最大，从偏离平衡位置角度θ到平衡位置过程，由动能定理可得联立解得在平衡位置处绝缘线对小球的拉力最大，由牛顿第二定律得联立解得

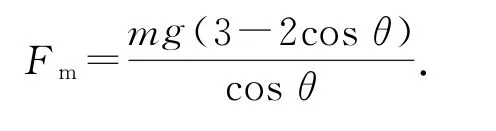
点评

叠加场中的简谐运动主要是带电物体参与的类弹簧振子与类单摆两种模型.解决这类问题的关键，一是找到合场力作用下的平衡位置)二是找到提供回复力的力(洛伦兹力不提供)；三是明确条件：类单摆最大摆角小于5°，类弹簧振子在弹性限度内，从而根据简谐运动的特征方程、动能定理、几何关系等规律解决相关问题.

2.6 分子（或原子）力场

例6在研究物理学问题时，为了更好地揭示和理解物理现象背后的规律，我们需要对研究对象进行一定的概括和抽象，抓住主要矛盾，忽略次要因素，建构物理模型.谐振子模型是物理学研究振动问题时所涉及的一个重要模型.

(1)如图13所示，在光滑水平面上两个物块A与B由弹簧连接(弹簧与A、B不分开)构成一个谐振子.初始时弹簧被压缩，同时释放A、B，此后A的v-t图像如图14所示(规定向右为正方向).已知mA＝0.1 kg，mB＝0.2kg，弹簧质量不计.在图14中画出B物块的v-t图像并求初始时弹簧的弹性势能Ep.

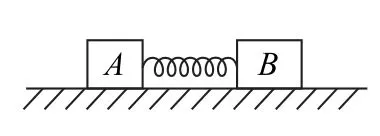
图13

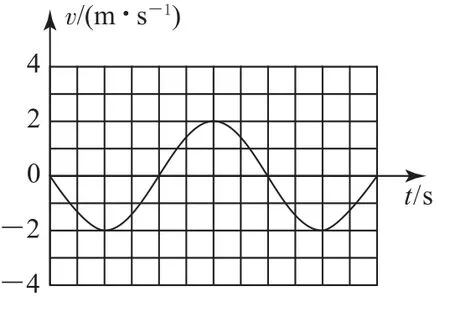
图14

(2)双原子分子中两原子在其平衡位置附近振动时，如图15所示，这一系统可近似看作谐振子，其运动规律与(1)的情境相似.已知两原子之间的势能Ep随距离r变化的规律如图16所示，在r＝r0点附近Ep随r变化的规律可近似写作r0)2，式中Ep0和k均为常量.假设原子A固定不动，原子B振动的范围为r0－a≤r≤r0＋a，其中a远小于r0，请画出原子B在上述区间振动过程中受力随距离r变化的图线，并求出振动过程中这个双原子系统的动能的最大值.

图15

图16

解析

(1)由图像14可 知，当vA＝－2 m·s－1时 弹簧恢复到原长，由动量守恒定律有0＝mAvA＋mBvB，代 入已知得vB＝1m·s－1.B物块的v-t图像如图17所示.由机械能守恒定律得

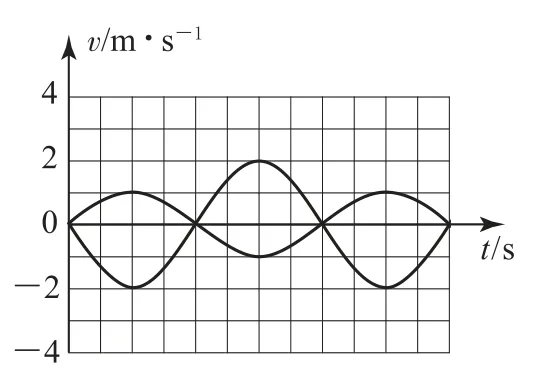
图17

(2)原子B振动过程中受力随距离变化的图像如图18所示，由题意可知，原子B处于r1＝r0处时，系统的动能最大，设为Ek1，系统的势能最小为Ep0.原子B在r2＝r0－a处时，系统的动能为0，系统的势能最大为，由能量守恒定律得Ep1＋Ek1＝Ep2＋0，联立得

图18

点评

分子(或原子)力场中的简谐运动，主要是分子(或原子)之间的作用力满足或近似满足F＝－kx时的类弹簧振子模型.解决这类问题的关键，一是找到平衡位置点(r＝r0)；二是看分子或原子间的作用力与其间距的关系是否近似线性关系)三是看分子或原子势能与其间距的关系是否近似线性关系)四是明确分子(原子)动能与势能之和是否为定值.

总之，简谐运动的应用要明确对象模型、场景模型各自特点与分类，聚焦共性：平衡位置、回复力F＝－kx、对称性、简谐运动的物理量及其特征方程，明析各种简谐运动类型的差异，综合运用波动振动关联、牛顿运动定律、动能定理、能量守恒定律、动量定理、动量守恒定律、电磁场与电路知识、宏观微观关联等规律，结合微元法、等效法、图像法、数理思维法等科学思维法解决相关问题.