一道动力学竞赛试题的多解赏析
——以第38届全国中学生物理竞赛预赛第8题为例
2022-02-22昌明彦赵相标
昌明彦 赵相标
(贵州省思南中学)
动力学类试题不仅是高考的高频考点,也是竞赛的高频考点.本文采用多种方法解析第38届物理竞赛预赛第8题,旨在激发学生参加物理竞赛的兴趣,提高学生科学思维能力.
1 原题再现
例一质量为m、半径为R的均质小球静止在水平桌面上,小球和桌面之间的动摩擦因数为μ,最大静摩擦力等于滑动摩擦力,重力加速度大小为g.用一根水平轻杆击打小球,击打位置位于球心所在的水平面上,击打方向正对球心,击打时间极短,小球获得的水平冲量为P.从击打结束开始经_________时间后小球开始纯滚动,小球开始纯滚动时的速度为_________.已知小球绕球心的转动惯量
2 试题分析
根据题意可知:轻杆水平击打小球球心所在位置瞬间,小球获得水平冲量P后向前滑动,小球质心初速度为小球与水平桌面上接触点向前滑动,水平桌面给接触点向后的滑动摩擦力,竖直方向小球受到的重力和支持力的合力为0,在滑动摩擦力的作用下质心做匀减速直线运动,同时小球绕质心做匀加速转动,可知小球为刚体模型,非质点模型.故解答此题既需要力与平动相关知识,还需力与转动相关知识.
3 知识储备
1)质点模型(高考知识点)
牛顿第二定律F=ma.匀变速直线运动中,速度v=v0+at,位移
线速度与角速度的关系为v=ωR.动能定理W外=ΔEk.动量p=mv.冲量I=Ft.动量定理F合t=mv-mv0.
2)转动模型(竞赛知识点)
匀加速转动ω=ω0+βt,转动定律M=Jβ,角动量L=mvr=Jω,角动量定理MΔt=JΔω,角动量守恒定律L=Jω=mvr=mω2r.
注:M为刚体所受各外力对转轴的力矩的代数和,J是 转 动 惯 量,β是 角 加 速 度.
4 试题解析
设小球获得的水平冲量为P,质心速度为v0=角加速度为β,初角速度为0,经过t时间后小球纯滚动,纯滚动时角速度为ω.
解法1 牛顿运动定律
对小球质心由牛顿第二定律有μmg=ma,运动学公式为v=v0-at,纯滚动条件为v=ωR,角速度公式ω=βt,刚体转动定律

联立得
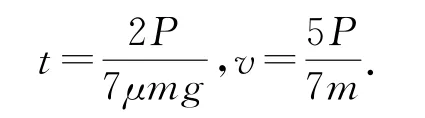
解法2质心动量定理
小球在向前运动的过程中,由质心动量定理有-μmgt=mv-P,刚体转动定律μmgR=Jβ,上式两边同时乘t得μmgRt=Jβt=Jω,纯滚动条件为v=ωR.联立得

解法3小球与水平桌面接触点合速度vt=0时,小球开始做纯滚动.
接触点随质心同速向前平动,开始时绕质心转动的线速度为0,可得接触点合初速度为v0.小球在水平桌面上运动过程中,质心做匀减速直线运动,接触点绕质心以角加速度β做匀加速转动,经过时间t,接触点合速度为vt=v0-at-βtR,质心由牛顿第二定律有μmg=ma.由小球转动定律有μmgR=Jβ.纯滚动条件vt=0,联立得

解法4角动量守恒定律
过小球与水平桌面接触点,垂直纸面向外为转轴,轻杆击打小球结束瞬间,小球获得的角动量(冲量矩)为L=PR.
重力、支持力、摩擦力过接触点的力矩都为零,得小球过接触点的角动量守恒,有PR=mvR+Jω.纯滚动条件有v=ωR.质心动量定理
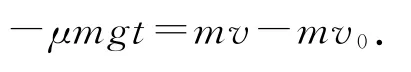
联立得

5 问题拓展
设小球恰好纯滚动时(t0=0)与桌面接触点为A,求此后t时刻小球上A点的速度和加速度大小.
分析小球达到纯滚动后,A点绕质心匀速转动,质心向前匀速平动,A点绕质心的线速度与质心平动的速度大小相等(v线=vC=v).此问属于运动学知识,A点运动轨迹为曲线.
解法1以A点为原点,水平向右为x轴,垂直水平面过A点竖直向上为y轴,建立坐标系.经过t时间后小球上A点转动的角度为如图1所示.
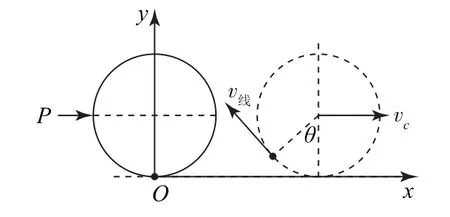
图1
由位移公式得

以上两式两边对时间求导数得A点分速度为

A点合速度为

将A点分速度对时间求导数得,A点的分加速度为点加速度大小

解法2A点的运动轨迹为曲线,由矢量三角形法则求A点速度和加速度.
小球达到纯滚动后,球上A点既随质心向前平动,又绕质心转动,A点的速度为质心的速度与绕质心转动的线速度的矢量和,三个速度组成一个矢量三角形,如图2所示.
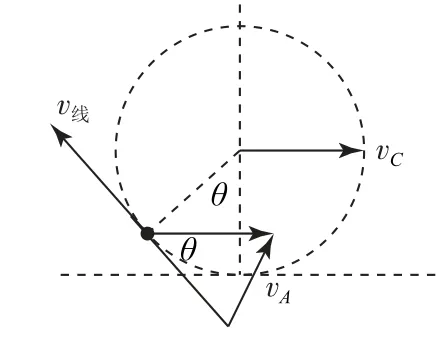
图2
由三角函数中的余弦定理得

或由等腰三角形几何知识得
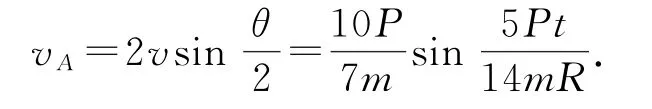
小球达到纯滚动后,质心做匀速直线运动,A点绕质心的向心加速度
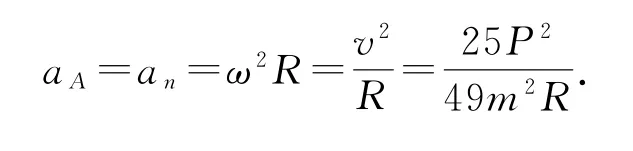
6 反思总结
原试题的第一、二两种解题方法分别应用动力学“三大观点”中的牛顿运动定律和动量定理求解,这两种方法对于高中物理尖子生来说容易上手;第三、四种解题方法将质心和接触点作为研究点,对接触点运用相对运动进行解析.问题拓展的第二种解法,运用学生非常熟悉的矢量三角形法则,已知分运动求合运动.对于高中生来说,解答此题的难点:一是小球运动属于刚体模型,不是质点模型;二是纯滚动的临界条件v=ωR或接触点相对于地面的速度为0;三是刚体模型转动过程中,刚体的转动定律、转动惯量、角动量、角加速度、角动量定理等.
