随机环境中受传染性疾病影响的分枝过程的极限性质
2022-02-21任敏
任敏
(宿州学院 数学与统计学院,安徽 宿州 234000)
0 引言
随机环境中的分枝过程(branching process,BPRE)最早由WILKINSON[1]于1967年提出,随后诸多学者对其进行了研究,并取得了丰硕成果。SMITH[2]给出了随机环境中的分枝过程几乎必然灭绝的条件,SMITH等[3-4]研究了随机环境和马氏环境中的分枝过程,李应求等[5]研究了随机环境中受控分枝过程的极限性质,任敏等[6]研究了随机环境中具有迁移的分枝过程的极限性质,谭珂等[7]、王玉萍等[8]研究了随机环境中受控分枝过程的极限性质和收敛速度等。关于随机环境中的分枝过程已有诸多研究成果,而关于随机环境中受传染性疾病影响的分枝过程研究较少,本文主要研究随机环境中受传染性疾病影响的分枝过程经适当规范化后{Wn,n∈N}和{,n∈N}几乎处处收敛和L1收敛的充分条件,{Wn,n∈N}L2收敛的充分条件,以及{Wn,n∈N}极限非退化到0的充分条件和必要条件等。
设(Ω,F,P)为一概率空间,(Θ,Σ)为可测空间,N为非负数集,N+为正整数集,ξ={ξn,n∈N}为(Ω,F,P)上 取 值 于(Θ,Σ)的 随 机 变 量 序 列。{Pi(θ);θ∈Θ,i∈N}和 {(θ)[1-αi,j(θ)]1-x;θ∈Θ,x=0或1,i,j∈N}为2个 概 率 分 布 列,记Pξ(⋅)=P(⋅|ξ),Eξ(⋅)=E(⋅|ξ)。
定义1若{Zn,n≥0}满足条件:
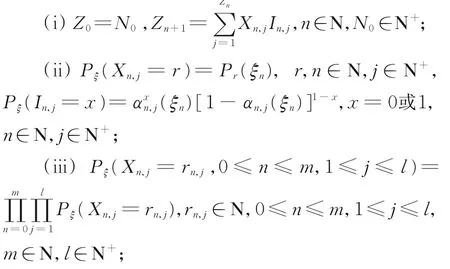
(iv)给 定ξ,{Xn,j,n∈N,j∈N+}为 独 立 同 分布随机变量序列,{In,j,n∈N,j∈N+}为独立随机变量序 列,{Xn,j,n∈N,j∈N+}和{In,j,n∈N,j∈N+}条件独立。
则称{Zn,n≥0}为独立随机环境ξ中受传染性疾病影响的分枝过程。其中,Zn表示第n代粒子总和,Xn,j表 示第n代第j个粒 子产生 的后代数;当第n代第j个粒子感染传染病毒未治愈时,In,j=0,当第n代第j个粒子未感染传染病毒或感染病毒已治愈时,In,j=1。
为方便讨论,引入记号:
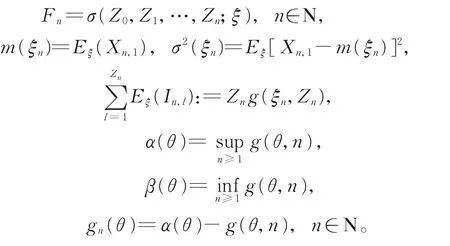
并 约 定0<P0(ξn)+P1(ξn)<1,0<αn,j(ξn)<1,i∈N,j∈N+,a.s.。
1 马氏性
引理1{Zn,n≥0}为随机环境ξ中的马氏链,其一步转移概率为
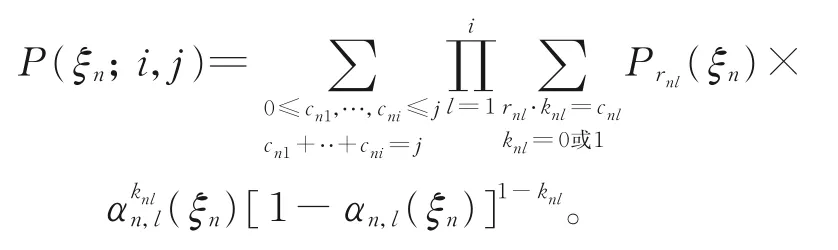
证 明由 于Z0=N0,易 知P{Z0=N0|ξ}=P{Z0=N0|ξ0}。
下证对任意的i1,i2,…,in-1,i,j∈N+,有
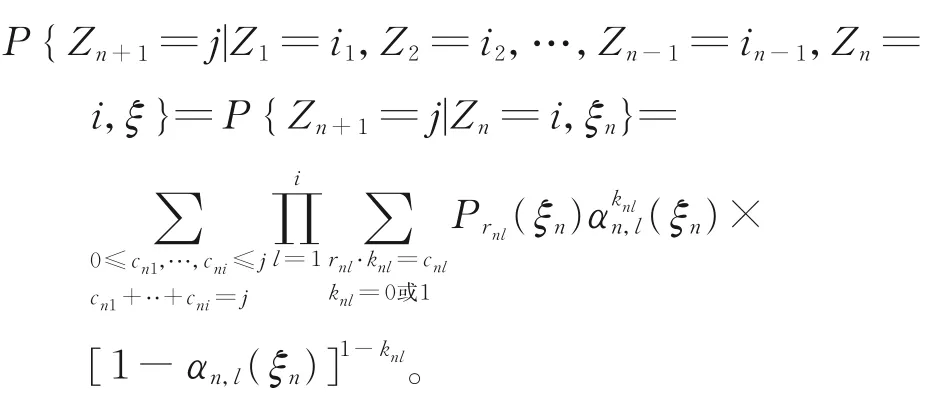
由{Zn,n≥0}的定义可得
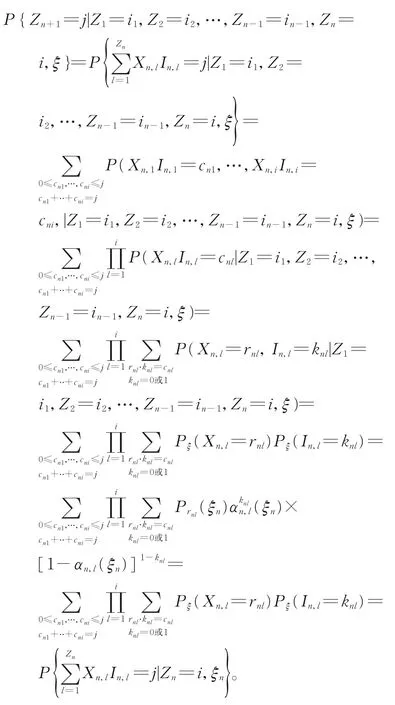
引理1得证。
引理2对任意的n∈N,存在:
(i)E(Zn+1|Fn)=Znm(ξn)g(ξn,Zn),a.s.,特别地,有
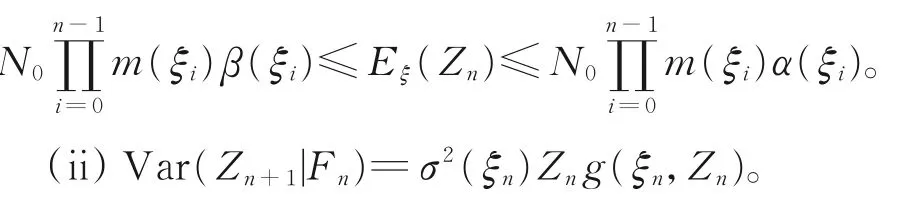
证明(i)由引理1,可得
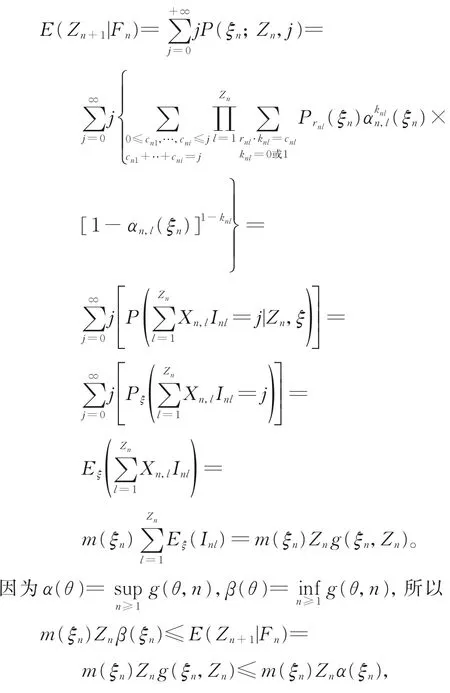
进而可得
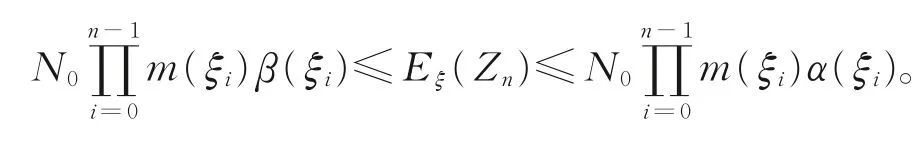
(ii)由引理1,可得
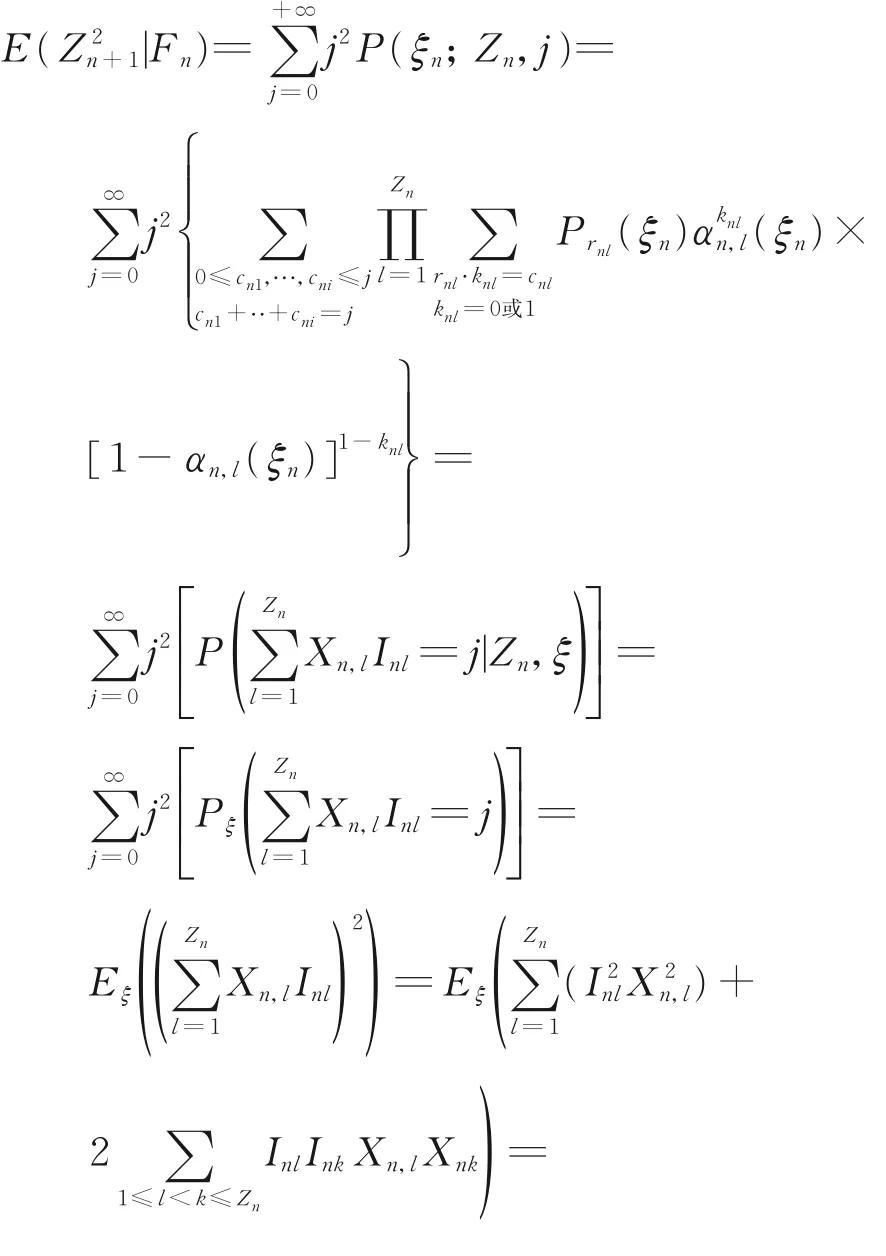
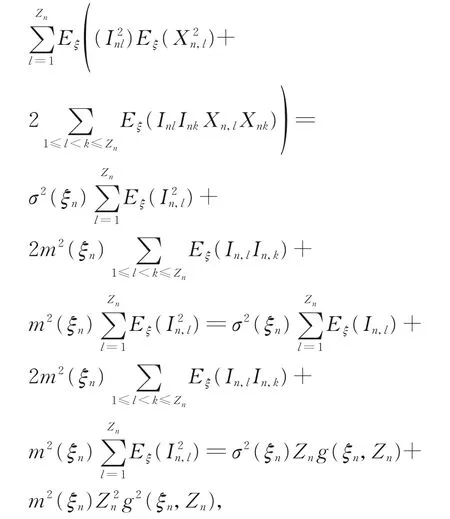
从而可得
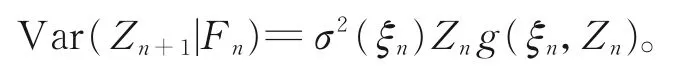
由于无法精确计算{Zn,n∈N}的条件均值,因此在取规范化因子时,考虑序列{Sn,n∈N}和{Un,n∈N},其中,
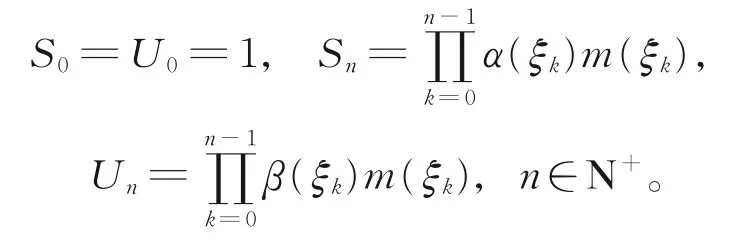
在适当条件下,利用{Sn,n∈N}和{Un,n∈N}规范化{Zn,n∈N},得 到 规 范 化 过 程{,n∈N}和{,n∈N},其中=Zn/Sn,=Zn/Un。
2 {n∈N}的极限性质
首先,给出{,n∈N}a.s.的收敛性。
定理1存在非负有限随机变量,使得
证明由引理2,可得
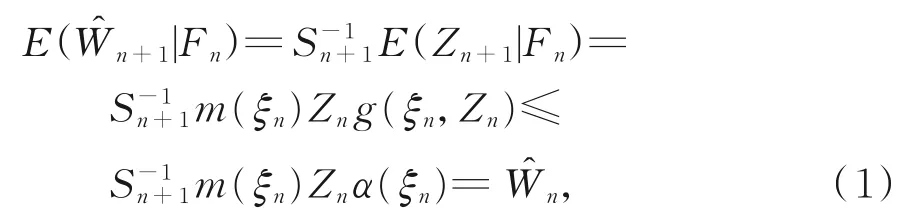
则{,Fn,n∈N}为非负上鞅。由上鞅收敛定理,可知存在非负有限随机变量,有

对式(1)两边关于Pξ(⋅)求期望,可得
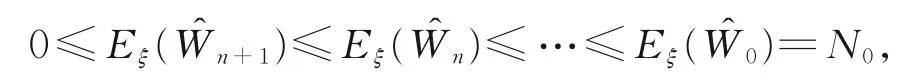
由Fatou引理可得
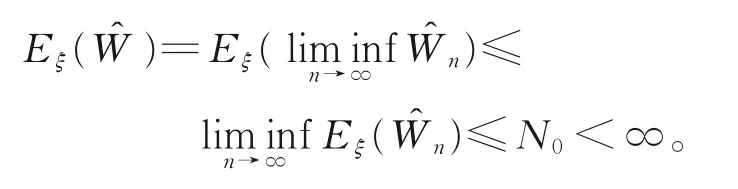
定理1得证。
其次,给出在一定条件下,{Wn,n∈N}L1收敛到几乎处处收敛的极限,即此时两种收敛是等价的,而通常两种收敛无必然关系。
定理2若则{W2n,n∈N}L2有界,且{Wn,n∈N}L1收敛于W。
证明由引理2可得
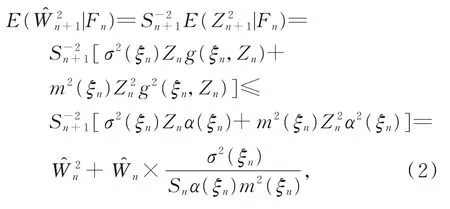
对式(2)两边关于Pξ(⋅)取期望,可得
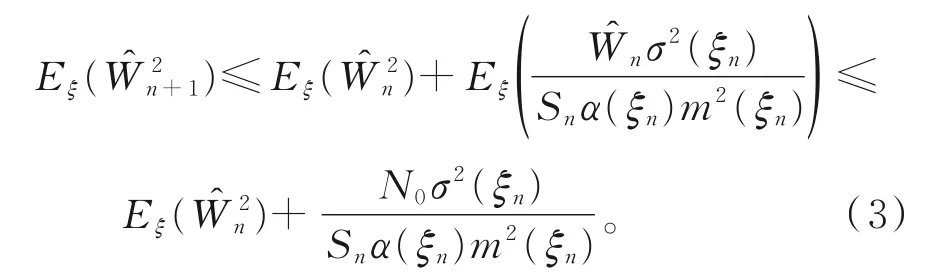
对式(3)两边取期望,可得
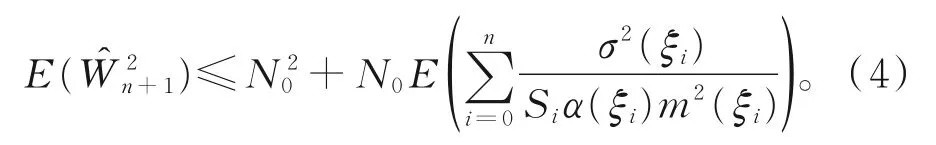
由 题 设 条 件 可 知,{W2n,n∈N}L2有 界,可 得{Wn,n∈N}一致可积。结合定理1,有Wn依概率收敛于W,从而可得{Wn,n∈N}L1收敛于W。
最后,讨论{Wn,n∈N}极限非退化的充分条件和必要条件。
引理3[10]设R+=(0,+∞),给定ξ,若对任意给定的n∈N,有
(i){λj(ξn),j≥1}是非 减序列,则在R+上存在 一 个 非 减 函 数φξn(⋅),使 得φξn(x)≥λ1(ξn),x>0;φξn(j)≤λj(ξn),j∈N+,且函数φ*ξn(x)≡xφξn(x),x>0为凸函数。
(ii){λj(ξn),j≥1}是非增序列,则在R+上存在一 个 非 增 函 数ψξn(⋅),使 得ψξn(x)≤λ1(ξn),x>0;ψξn(j)≥λj(ξn),j∈N+,且 函 数ψ*ξn(x)≡xψξn(x),x>0为 凹 函 数。
定理3若对任意的n∈N,{g(ξn,k)}k≥1为非减序列,且有
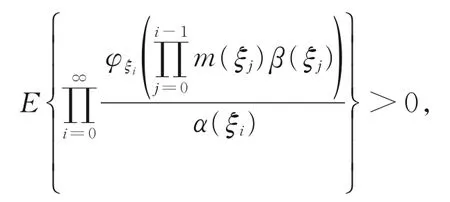
则E{W}>0,即P{W>0}>0。
证 明由 引 理2和 引 理3,结 合{g(ξn,k)}k≥1,∀n∈N的非减性,可知在R+上存在非 减 函 数φξn(⋅),n∈N和 凸 函 数(x)≡xφξn(x),x>0,n∈N,使得
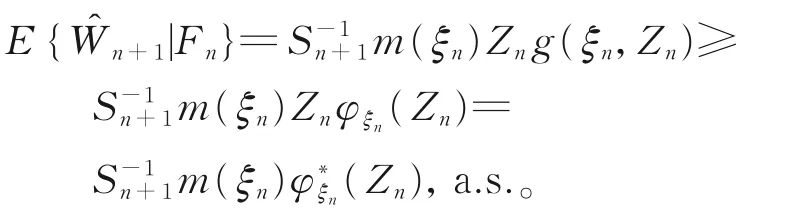
因为对任意的n∈N,φξn(⋅)为非减函数,且φ*ξn(⋅)为凸函数,所以结合Jensen不等式,可得
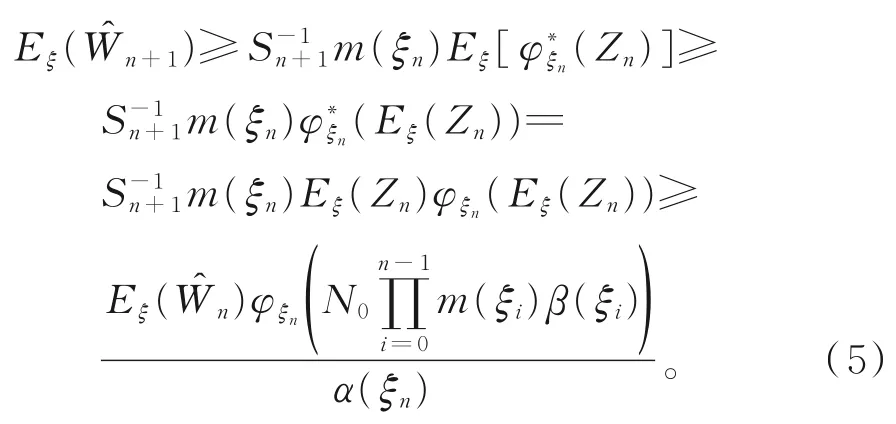
对式(5)关于n递推,可得
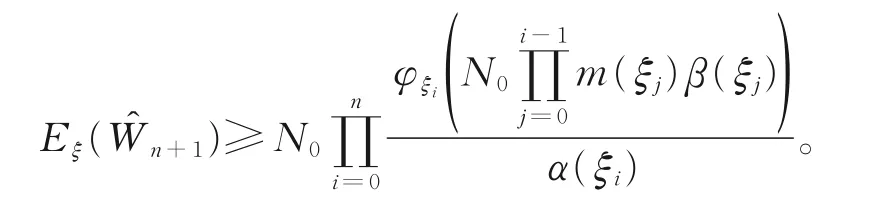
由题设条件和Fatou引理可得

于是可得P(W>0)>0。
证毕。
定理4若P{W>0}>0,则在{W>0}上,有
证明对任意的n∈N,由引理2,可得
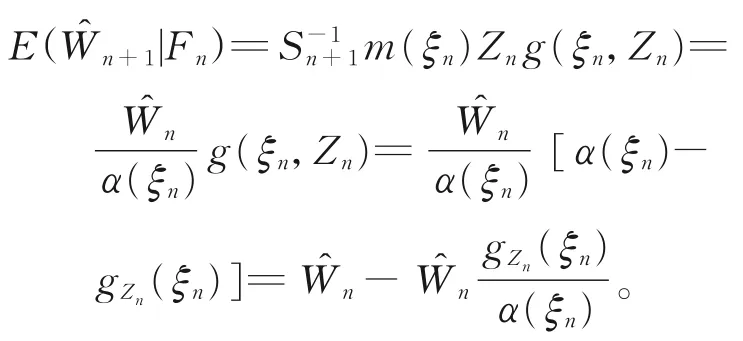
因此,有
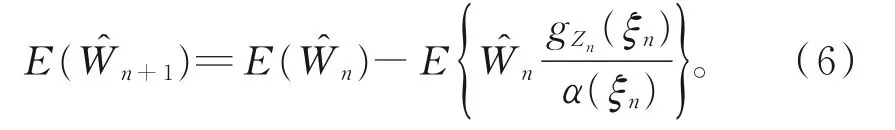
由E(W0)=N0和式(6),可得
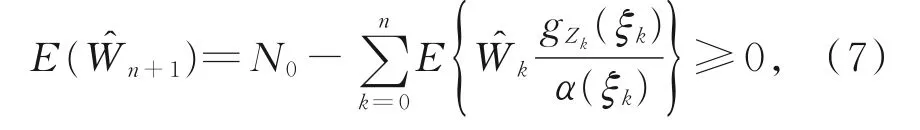
其中,令n→∞,有
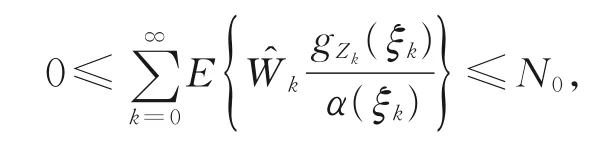
于是有
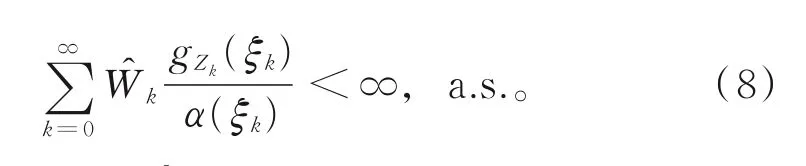
对几乎处处w∈{W>0},则有
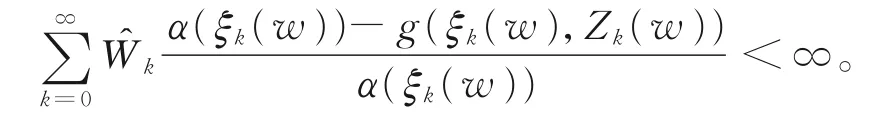
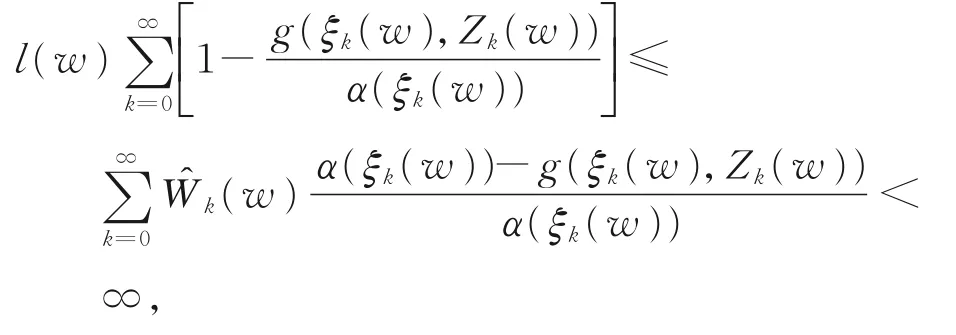
定理5若
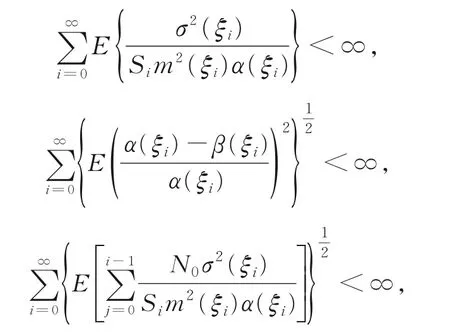
则{Wn,n∈N}L2收敛于W。
证 明因 为{Wn,Fn,n∈N}为 非 负 上 鞅,由Doob分解定理可知,对任意的n∈N,有
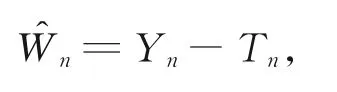
其中,{Yn,Fn,n∈N}为鞅,{Tn,n∈N}为增过程,且满足
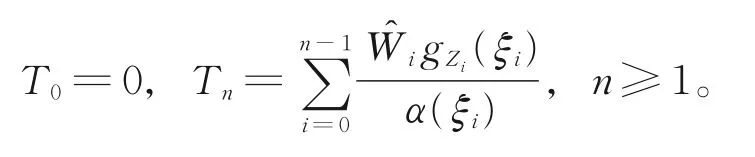
由于
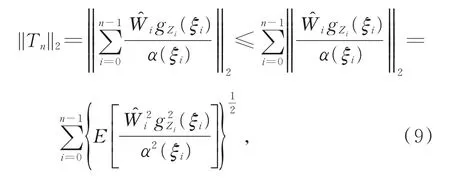
由式(3),可得
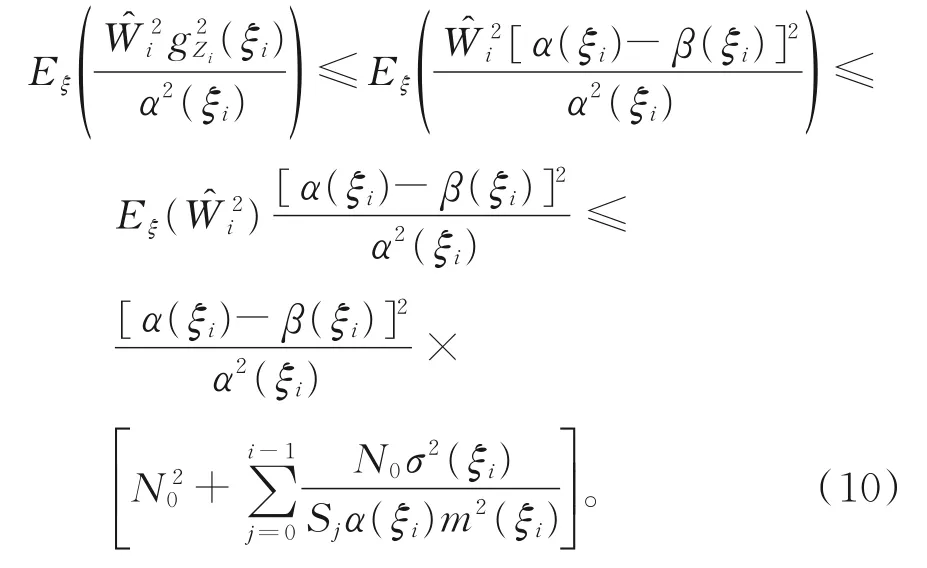
对式(10)两边取期望,可得

由式(9)和式(11),可得
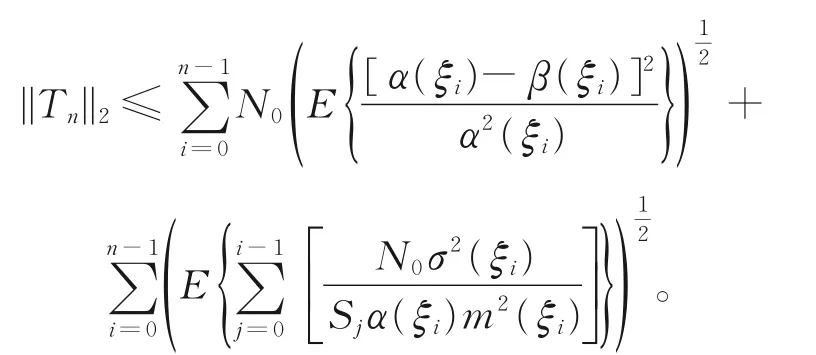
由题设条件,知{Tn,n∈N}L2有界。因为{Tn,n∈N}为非负增过程,从而可得{Tn,n∈N}L2收敛于某非负 随 机 变 量T。又 因 为{Wn,n∈N}L2有 界,故{Yn,n∈N}L2有界,且{Yn,Fn,n∈N}为鞅,则由鞅收敛定理,知{Yn,n∈N}L2收敛于某随机变量Y,从而可得{Wn,n∈N}L2收敛于随机变量W。
3 {,n∈N}的极限性质
定理6若则存在期望有限的非负随机变量,使得
证明由引理2,可知
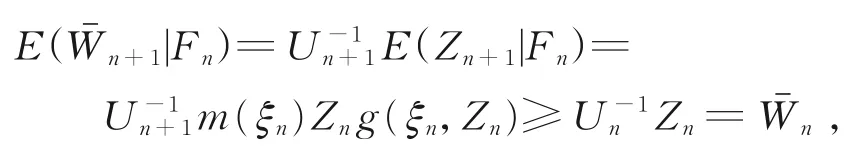
则{,Fn,n≥0}为非负下鞅。由引理2,可得
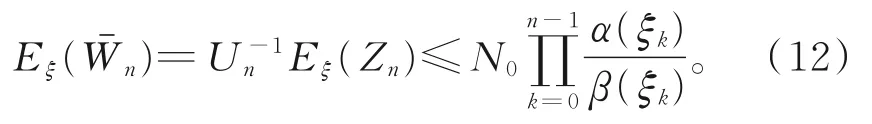
对式(12)两边取期望,得
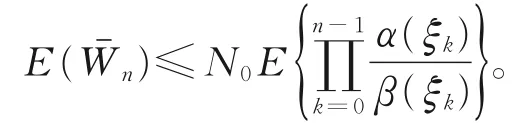
下面给出{,n∈N}L1收敛的充分条件。给定ξ,对任意的n∈N,记
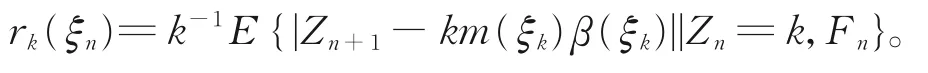
定理7若
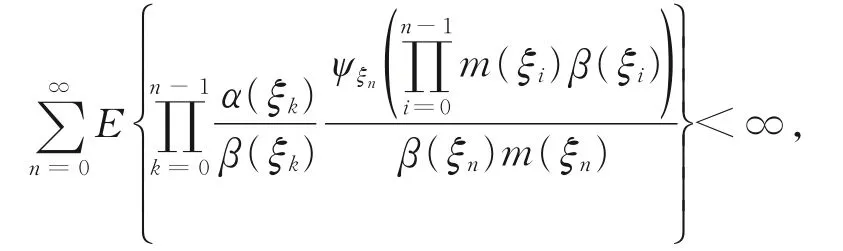
且{rk(ξn),k≥1}为非 增序列,则{,n≥0}L1收敛于某非负有限随机变量。
证明由引理3结合{rk(ξn),k≥1},对∀n∈N的非增性,知在R+上存在非增函数ψξn(⋅),n∈N和凹函数ψ*ξn(x)≡xψξn(x),x>0,n∈N,使得
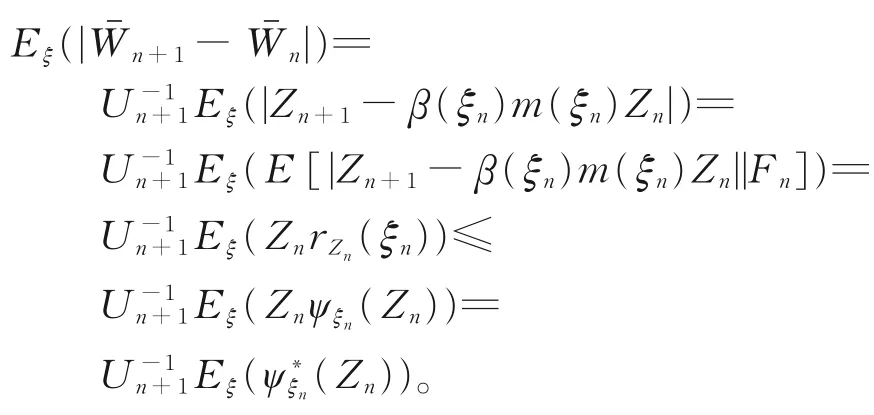
因为ψξn(⋅)为非增序列,ψ*ξn(⋅)为凹函数,由Jensen不等式,可得
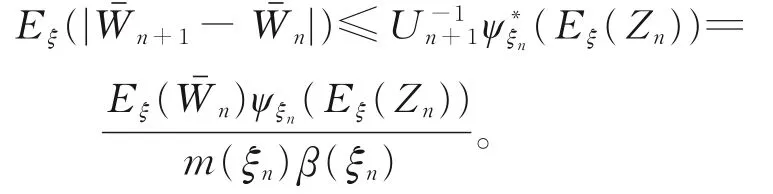
由引理2,可知
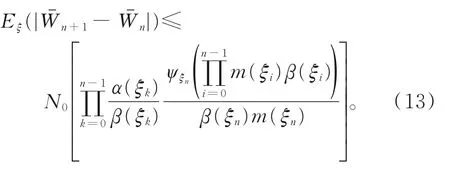
对式(13)两边取期望,可得
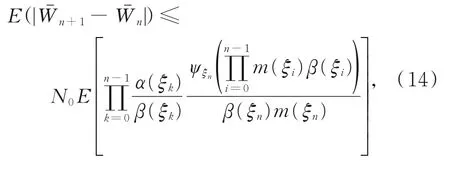
对式(14)两边求和,由题设条件,可得
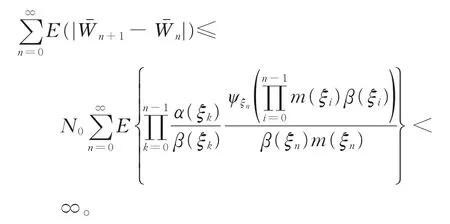
所 以{,n≥0}为L1柯西序列,从而{,n≥0}L1收敛于某非负有限随机变量。
