基于动态模态分解的长江口海表温度时空分布特征重构研究

陈嘉星，江迪，张霄宇，3，4*

（1.浙江大学地球科学学院，浙江 杭州 310027；2.浙江大学信息与电子工程学院，浙江 杭州 310027；3.浙江大学海南研究院，海南 三亚 572000；4.浙江大学海洋研究院，浙江 舟山 316000）

海洋表面温度（sea surface temperature，SST）是海洋-大气系统物质和能量交换过程的重要参数之一，是海水热量传递的直接表现形式，SST的变化可影响海洋-大气系统之间的热量交换，进而影响区域气候［1-2］。

长江口海域陆地、海洋、大气及人类活动等过程的相互作用强烈，水动力过程复杂，长江口海洋表面温度的分布特征与变化趋势影响并指示海水运动，是该海域海洋复杂内在动力机制的综合表现。此外，SST与表层叶绿素a浓度分布、海洋养殖、海洋生物的分布等密切相关［3］。研究长江口海洋表面温度的时空演变规律对于理解时空耦合系统的深层动力机制、浅海环流及物质输运等过程极为重要。

关于长江口海洋表面温度的时空分布特征，前人已有不少研究。周晓英等［4］利用功率谱分析、MK突变检验分析了水文站的月均海温数据和径流量数据，研究发现长江口海温的最高值出现在8月，最低值出现在2月，季风和长江径流对其有显著影响。孙凡等［5］基于1982—2016年的OISST数据及其他气象数据，采用回归分析和滞后相关系数法进行了研究，结果表明，长江口海域海表温度的长期升温趋势主要受该区域径向热输送及长江平流热输送增强的影响。买佳阳等［6］基于2000—2012年的中等分辨率成像光谱仪（moderate-resolution imaging spectroradiometer，MODIS-Terra）LIB数 据，通 过优化劈窗算法，建立了适合长江口水域的海表温度反演模型，并进行了海表温度反演，分析发现，长江口海表温度主要受太阳辐射影响，且口内口外的海表温度具有不同的季节性差异。何全军等［7］基于2015—2017年我国周边海域的卫星数据和现场数据，采用多元回归模型，开发了适用于FY-3C/VIRR数据的区域SST反演算法。AI等［8］利用渤海地区的晴天红外遥感数据和浮标实测数据，构建了一种适用于渤海地区的SST神经网络反演模型，并将反演结果与MODIS的SST产品进行了精度评估，结果表明，深度学习可应用于SST反演。以上研究或偏向于水文资料分析，受水文站分布限制，分析仅局限于某几个固定点位，无法扩展至整个海域；或注重海温反演模型的建立，其反演模型是基于实测站位建立的，但研究选取的实测站位是否可代表整个海域有待商榷，同时也缺乏对长江口海温时空演变模式的模态分析。

20世纪以来，遥感技术迅速发展，借助遥感手段可获得长时序、全覆盖的SST数据。但因云层、雾、霾等影响，常常出现数据缺失问题，为获得具有连续时间序列的全覆盖卫星遥感资料，国内外已有多种数据插值方法，如克里金插值法、最优插值法、期望最大化法、奇异谱方法、本征模态分解法、卡尔曼滤波法等。其中大多受限于数据的原始状况，或依赖相关的参数和先验值等信息，在适用性以及计算效率上均受限制。经验正交函数分解法（data interpolating empirical orthogonal functions，DINEOF）是目前较为有效的遥感数据重构方法，具有无需先验值、自适应、时空相关，以及适用于大面积缺测数据重构等传统重构方法不具备的优势［9-10］。

动态模态分解（dynamic mode decomposition，DMD）是Schmid于2008年提出的一种数据分析方法，其本质是将高维非线性系统矩阵转化为低维线性系统的过程，已被广泛应用于股票价格预测、图像压缩处理、物理流场分析等数据处理研究［11-13］。当数据的缺失率过高时，DINEOF具有很好的重构效果，在能够获得足够时序数据的情况下，数据驱动的算法能够更好地解决动态系统的采样问题。海洋是一个典型的高维动态系统，尤其在近岸区域，受潮汐、风浪等因素影响，数据随时间动态变化剧烈。因此，可将其视为由许多不同频率的组分组成，DMD算法求得的模态和特征值分别描述了系统的空间特性和时间特性，符合相关海洋表面温度研究的要求。DMD按照频率对系统进行排序，提取系统特征频率，观察不同频率的流场结构对流场的贡献，同时DMD模态特征值可预测流场［14］。在能够获取足够时序数据的情况下，DMD算法可以更好地解决动态系统的采样问题，从而实现对海洋表面温度的预测。

在实际应用中，由于数据维度高、样本数量大、数据本身存在噪声等问题，DMD算法需针对具体应用场景做相应改进。考虑海洋学的研究特性，为节约成本、提高效率并为实际站位布设提供参考，本文拟结合正交三角（orthogonal right triangular，QR）分解算法［15］通过典型观测站位还原SST时空分布情况，进行精度校验，并与单一DMD算法进行比较。

本文采用2003年1月至2019年12月MODIS L3级月平均SST遥感数据，主要开展两方面工作：（1）用DMD算法获得SST基本模态，并结合QR分解算法获得典型观测站位；（2）分别利用DMD算法、DMD结合QR分解算法对SST数据进行重构，并评价2种算法的重构精度，对误差原因进行初步分析。

1 研究区域概况

如图1所示，研究区域位于118°E～128°E，26°N～34°N，为长江口及其邻近海域，区域内主要入海河流为长江和钱塘江等。长江口区域位于东亚季风区，夏季盛行西南风，冬季盛行东北风。水文结构一方面受近岸的长江冲淡水和沿岸流影响：北有低温、低盐、高沙的黄海沿岸流沿苏北南下，西有低盐、中沙的长江冲淡水输入，其影响范围存在季节性差异；另一方面受外海的台湾暖流和黑潮次表层水的相互作用，两者从台湾岛附近侵入，沿约200 m等深线北上，控制陆架外缘地区，但存在明显的季节性差异［16-17］。此外，长江冲淡水与台湾暖流混合水团的盐度梯度明显，主要影响长江口外羽状锋区域［18-19］。除季风与环流相互作用外，长江口区域还受潮汐、风浪等因素影响，导致长江口区域的水动力环境较为复杂，进而影响SST的时空分布。

图1 研究区域地理位置示意［16-17］Fig.1 Geographical map of the study area［16-17］

2 数据和方法

2.1 MODIS/SST

MODIS中分辨率成像光谱仪是一种“图谱合一”的光学仪器，可获取从可见光到红外共36个波段的观测数据，其最大空间分辨率为250 m。MODIS可提供包含陆地、海洋、云、大气、温度等特征信息的数据产品，广泛用于陆地、海洋及大气环境监测等领域［20］。

考虑数据的时间连续性、适中的空间分辨率以及获取数据的便捷性，选用2003—2019年MODISAqua遥感器的L3级月平均SST产品，数据从https：//oceandata.sci.gsfc.nasa.gov/获取。空 间分辨率为4.6 km×4.6 km，每帧影像大小均为240×192，时间帧为204帧，各参数的观测像元总数均为9 400 320个，且均采用NetCDF4格式。NetCDF4是一种科学数据存储格式文件，能分层存储数据，且可用C、Fortran和MATLAB等语言进行操作。

前处理主要包括掩膜制作、数据缺失率统计及空白数据填补、去噪处理等。

首先，获取全球海岸线shp文件（网址：https：//www.ngdc.noaa.gov/mgg/shorelines/data/gshhs），导出研究区域的shp文件，并将导出的shp文件在ARCMAP中进行完善。然后，在MATLAB中将shp文件转化为矩阵格式掩膜，令陆地部分为0，海洋部分为1，为方便处理，将陆地中的湖泊和河流赋值为0。掩膜处理完成后，统计海洋数据，数据缺失率为1.57%。因数据缺失率较低，考虑程序的运行效率，用每帧的平均值填补空白数据。最后，对填补完成的数据进行去噪处理。

2.2 DMD算法原理

将海洋视为由不同频率的组分组成的高维非线性系统，由DMD算法得到的模态描述其空间特性。下面介绍DMD算法的原理。

首先，从数值仿真或实验中收集N个时刻的快照，形成数据矩阵{ψ0，ψ1，…，ψN}，第i个时刻的快照为第i列，假设上述数据矩阵在时间上是等距的，时间步长为Δt。利用快照序列构建2个时间相邻数据矩阵：

利用连续快照之间的线性关系，通过矩阵A将式（1）中的2个快照矩阵相连接。矩阵A为高维系统的系统矩阵，包含大量动态关系，反映系统的动态特征。由于矩阵A的维数高，需要对其进行降阶处理。动态模态分解提供了矩阵A的低阶表示方法：

DMD通过对上述快照矩阵进行数学变换，提取主导特征值及主要模态。本征正交分解（proper orthogonal decomposition，POD）又称主成分分析，将高维系统表示为少量POD模与其对应系数的线性组合，从而实现对高维系统降维。本文拟采用奇异值分解与POD相结合的方法，通过奇异值分解对高阶算子进行相似变换，此方法具有较好的数值稳定性。

利用X的POD模，寻找秩为r的矩阵F，近似表示高维矩阵A：

其中，U为通过对X进行奇异值分解所获得的POD模，U*为酉矩阵，有

其中，Σ为对角矩阵，对角线元素为r个奇异值，对应特征值σ1，σ1，…，σr，同时奇异值分解得到的酉矩阵U和V满 足：

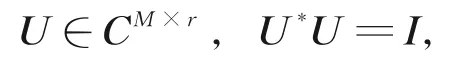
F的求解过程可看作将X和Y之间的Frobenius范数最小化，将式（3）和（4）代入，得到

求解式（6），得到

可用F近似表示A，记F的第i个特征值为μi，特征向量为ωi，则第i个DMD模态为

由以上定义可知，模态是所研究的系统中具有某种全局特征的结构，本文研究的全局特征是SST的“频率”，即SST的变化率。另外，若特征向量为实数，则对应的特征向量随特征值的正负变化分别呈指数级增长或衰退。

2.3 DMD结合QR分解算法确定典型观测站位

DMD算法仅能解决理想情况下流场基本模态的获得及预测问题。在实际应用中，由于数据维度高、样本数量大、数据本身存在噪声等，需根据具体应用场景对DMD算法做相应改进。QR分解算法用以求解矩阵特征值，可提高求解速度。用QR分解算法选择典型观测站位的思路是，对于给定的典型观测站位数k，通过寻找最佳置换矩阵最大化|detAk|（det为矩阵的行列式值，Ak为QR分解算法中的上三角矩阵），寻找稳定、准确的典型观测站位［21］。考虑海洋学的研究特性，本文拟结合QR分解算法计算最佳模态数和典型观测站位数，利用典型观测站位还原海温数据。

2.4 数据处理流程

数据处理流程如下：

（1）下载原始数据，构造矩阵。用制作好的掩膜，剔除每个时间帧原始数据中的陆地和岛屿，只保留海洋部分的数据，计算平均值，用平均值替代其中的NaN（not a number），最后展开为列向量，有效数据共n个。对数据进行去噪处理，同时以p次间隔（p=204，时间间隔设为一个月）的观测数据构建矩阵Xp×n，时间设定为起始时间t1到结束时间tq，且满足tq=tq-1+Δt。

（2）抽取前80%的连续数据作为训练数据，数据量为m（m=163，时间间隔为一个月），其余的20%作为预测数据，数据量为q（q=41，时间间隔为一个月）。

（3）由上述训练数据矩阵Xm×n构造子矩阵。令子矩阵的时间间隔为Δt，得到Xm-11，Xm2：

（4）求特征值和特征向量。经步骤（3）后得到2个子矩阵，对X1m-1进行奇异值分解，Σ、U、V*分别为奇异值、左奇异向量、右奇异向量，同时结合矩阵计算低阶矩阵F的特征值及其特征向量。

（5）将得到的特征值和对应的特征向量组成矩阵，根据QR分解算法，确定最佳模态数和最佳典型观测站位数，并将其代入FDMD中，重构历史数据。

3 结果与讨论

3.1 长江口长时序SST的DMD模态分解

利 用2003—2019年 的MODIS L3级 月 平 均SST产品，由DMD得到SST的主要时空演变模态，用这一典型非线性动力学现象说明DMD在海洋系统中的应用过程。训练数据的时间段为2003年1月至2016年7月，预测数据的时间段为2016年8月至2019年12月。

将DMD结合QR分解算法寻找典型观测站位的方法（以下简称典型观测站位还原法）应用于上述训练数据，得到的重构误差与典型观测站位数的关系如图2所示。

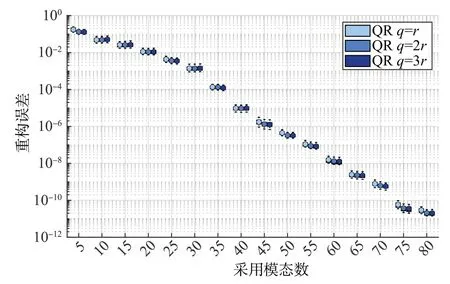
图2 典型观测站位效果对比Fig.2 Comparison of effect of typical observation stations

其中，重构误差用均方根误差（root mean square error，RMSE）表征，p表示典型观测站位数，r表示DMD模态数。由图2可知，均方根误差随DMD模态数的增加而降低，且若DMD模态数不变，通过增加典型观测站位数能有效降低重构误差。DMD算法得到的主要模态如图3所示（因篇幅所限，此处只给出前4个模态）。

图3 用DMD算法分解长江口海域SST数据得到的前4个主要模态Fig.3 The first four main modes decomposed by DMD algorithm of SST data in the Yangtze River Estuary

由图3可知，模态1在整个海域表现为负相关，从空间分布看，苏北沿岸、长江口及杭州湾和浙闽沿岸区域是SST变化率绝对值较大的区域，变小很快，且随着长江冲淡水的外推呈舌状递增状态，而SST变化率绝对值较小值出现在冲绳岛西北海域的大洋区域，变小很慢。推测出现这种分布的原因可能由近岸区域受陆地径流输入的淡水与海水混合所致，而低值区受黑潮和台湾暖流影响，海水性质比较均一。季节特征表现为由秋入冬。

模态2中SST变化率与近岸区域及南侧海域呈正相关、与中北侧海域呈负相关，表明2个区域呈现相反的变化趋势。这可能反映地形对SST的影响，苏北沿岸、长江口及杭州湾、浙闽沿岸区域水浅、比热容小，易受大陆气温和沿岸流的影响，SST变化率最大值高于0.02℃，呈现SST变大、变快的特征；南侧海域受黑潮和台湾暖流的影响，表层SST变化不大；中北侧由于远离陆地，受环流影响小，SST变化率呈负值。季节特征表现为由春入夏。

模态3中SST变化率呈正、负2种分布情况，苏北沿岸、长江口及杭州湾、浙闽沿岸区域及北侧海域为正值区域，南侧海域为负值区域。这与第1模态所反映的受冲淡水、环流的影响相同。但季节特征表现为由春入夏。

模态4则表现为近岸部分和150 m等深线以外的大洋区域为SST变化率正值区，大致为被30 m和150 m等深线所夹区域为SST变化率负值区。这与第2模态反映的地形影响一致。但季节特征表现为由秋入冬。

3.2 DMD结合QR分解算法获取典型观测站位

上述结果表明，当DMD模态为25、典型观测站位为25时，重构误差已经相当小。因此，考虑运行速度和重构精度，本文选取25个DMD模态、25个典型观测站位对长江口海域的海表温度进行稀疏还原，结果如图4所示。

图4 2016年8月长江口海域SST数据稀疏还原结果Fig.4 The results of sparse restoration of SST data in Yangtze River Estuary in August 2016

由图4可知，相比单纯采用DMD算法，DMD结合QR分解算法的还原结果能很好地代表整个海域，海温分布与真值更接近。因此，若不考虑成本和运行速度，单一追求重构精度，用DMD算法能得到更高精度的还原结果。若综合考虑成本、运行速度、重构精度，则DMD结合QR分解算法的重构表现更佳。

3.3 精度分析

选取2016年8月相同区域的原始数据与重构数据的像元值进行精度评价，评价结果如图5所示。从图5（a）和（b）的对比中可知，2种方法的原始值与重构值集中分布在直线y=x附近，精度指标均较理想。其中，DMD结合QR分解算法的RMSE为0.005 0。据统计结果，测试数据集的历史数据与DMD结合QR分解算法重构数据之间的RMSE在0.005 0～0.011 2，平均值为0.007 6。因此，虽然在精度上DMD算法的最佳还原结果比DMD结合QR分解算法的还原结果表现更佳，但考虑运行速度和成本，仍可认为DMD结合QR分解算法的结果较好。

另外，由图5可知，无论是DMD算法还是DMD结合QR分解算法重构得到的结果均具有相当高的精度。为进一步分析重构效果，随机选取2个典型观测站位，对其原始值、DMD最佳还原值、典型观测站位还原值做对比分析。

由图6可知，DMD最佳还原值和典型观测站位还原值与原始值耦合良好，说明DMD算法和DMD结合QR分解算法均较合理可靠。因此，可以认为选取的25个典型观测站位能较好地代表整个研究海域海洋表面温度的分布特征。这与图5的DMD算法和DMD结合QR分解算法的结果高度吻合。

为更好地评价2种方法的重构效果，选择预测数 据 集 中 的2017年4月、2017年7月、2017年10月及2018年1月（分别代表春、夏、秋、冬4个季节）进行重构，得到的结果如图7所示。

由图7可知，从空间分布上看，2种方法的重构结果均与原始值的趋势保持一致，误差较小，这与图5和图6得到的结论一致。

图5 2016年8月的SST重构精度Fig.5 The accuracy of SST reconstruction in August 2016

图6 某2个典型观测站位重构前后对比Fig.6 Comparison of reconstruction of two typical observation stations

图7 长江口海域典型年份四季SST数据稀疏还原结果Fig.7 Sparse restoration results of SST data in four seasons of a particular year in the Yangtze River Estuary

4 结论

基于DMD算法的基本理论，将QR分解算法应用于海洋学观测，分析了长江口海域的海温数据。结果表明，DMD结合QR分解算法对长江口海温数据进行稀疏还原，能有效去除噪声，填补缺失数据。增加DMD模态数能有效降低重构误差，当模态数一定时，可通过增加典型观测站位数降低重构误差。当采用25个模态、25个典型观测站位时，重构数据的RMSE为0.005 0。

DMD算法分解得到的前4个模态中，模态1和模态3可能反映了长江冲淡水及环流的影响，模态1的季节特征为由秋入冬，模态3则为由春入夏；模态2和模态4可能代表海底地形的影响，模态2季节特征为由春入夏，模态4则为由秋入冬。

在数据充足的情况下，DMD算法能很好地解决动态系统的采样问题，对时序数据的重构和分析具有应用价值。单纯采用DMD算法重构，精度相对较高，但采用DMD结合QR分解算法重构效率较高，并且可在稀疏站位条件下重构海洋温度场，这对海洋学调查尤为重要。