半圆形粗糙元壁面颗粒沉积数值模拟研究

2022-02-21黄秋焰罗坤樊建人

浙江大学学报（理学版） 2022年1期

黄秋焰，罗坤，樊建人

（浙江大学能源工程学院，浙江杭州 310027）

随着工业化的进步和人们生活水平的提高，粉煤燃烧发电工厂、汽车废气和建筑烟气等带来细微颗粒的排放，使大气中的尘埃颗粒急剧增加，严重恶化的城市空气质量危害人类健康。细颗粒不仅对人体呼吸系统、心血管系统及中枢神经系统造成伤害［1-3］，而且易在气力输送、热交换器、粉末涂料设备等通风管道中沉积与悬浮［4-5］，影响设备的正常工作与运转。大多数通风设备的壁面都不光滑，存在大小不一、形式不同的粗糙元壁面。对粗糙元壁面通风管道颗粒沉积的研究可以为通风管道的设计提供指导。

与光滑元壁面相比，粗糙元壁面对颗粒沉积特性有加强作用。不同粗糙元壁面和粗糙元参数对颗粒沉积也有较大影响。国内外已经有大量相关研究，LAI等［6-7］通过实验研究了方肋形粗糙元壁面的颗粒沉积特性，结果表明相比于光滑元壁面，方肋形粗糙元壁面的颗粒沉积率有较大提高。LU等［8］通过数值模拟研究了多组方肋粗糙元间距高度比与粗糙元高度管径比参数下的颗粒沉积加强特性，发现当粗糙元间距高度比为2，高度管径比为0.1时，颗粒沉积加强比可达100～1 000。HONG等［9］基于CFD-DEM方法分别对方肋形、尖角形、三角形粗糙元进行了三维数值模拟，结果发现，尖角形粗糙元的颗粒沉积率最大，而三角形颗粒沉积率最小。需要注意的是，尚未有学者对半圆形粗糙元壁面颗粒沉积进行研究。基于此，本文研究不同半圆形粗糙元壁面参数（粗糙元间距高度比p/e、高度管径比e/D）下颗粒沉积特性，并进一步与方形粗糙元壁面颗粒沉积进行了对比。

在颗粒沉积研究模型方面，众多粗糙元壁面的颗粒沉积研究［8-12］忽略了颗粒在壁面的反弹，将壁面假设为附着壁面，即当颗粒与壁面接触时认定颗粒沉积，这与实际情况不符。但也有学者在研究颗粒沉积时，考虑了颗粒的反弹、沉积、二次扬尘。如BRACH等［13］根据Johnson-Kendall-Roberts（JKR）理论，通过实验总结了将半经验反弹速度作为判断颗粒沉积的条件，较全面地考虑了颗粒反弹及沉积现象。SOLTANI等［14］采用临界动量理论判别了颗粒的二次扬尘情形，此方法被很多研究采纳［15-17］。

在颗粒沉积研究方法方面，数值模拟已经成为一种重要的研究手段。相比于雷诺时均（RANS）方法，直接数值模拟（DNS）与大涡模拟（LES）在处理工程问题时往往计算成本偏高。因此，RANS方法是工程领域中一种重要的数值计算方法。TIAN等［10］研究了不同湍流模型对颗粒沉积特性的影响，结果发现，雷诺应力模型（RSM）可以很好地预测颗粒沉积，这是由于RSM考虑了湍流的各向异性，可获得更准确的流场信息。RSM现已被广泛运用于颗粒沉积的数值模拟研究［8-9，18-19］。因此，本文采用RSM求解流场。另外，考虑颗粒浓度偏低，属于稀疏流，采用拉格朗日法对颗粒进行追踪。

1 物理模型

考虑工业设备的通风管道大多为矩形管，因此，选取二维矩形通风管道作为模拟对象，管道长400 mm，高度20 mm，如图1所示。管道下壁面分别用方形和半圆形粗糙元以不同e/D和p/e进行排列，如表1所示。管道上壁面为光滑壁面。空气从管道左侧进入，于右侧流出。

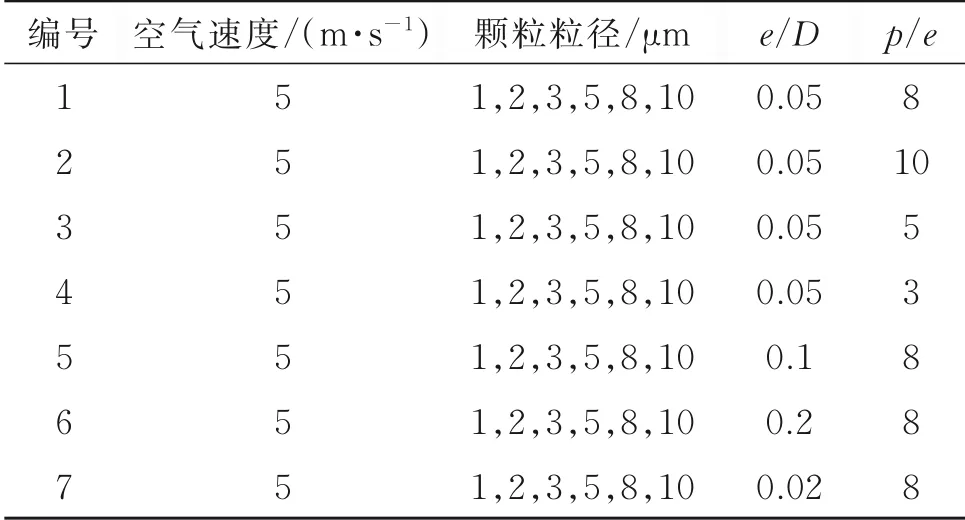
表1 计算算例Table 1 Computation case

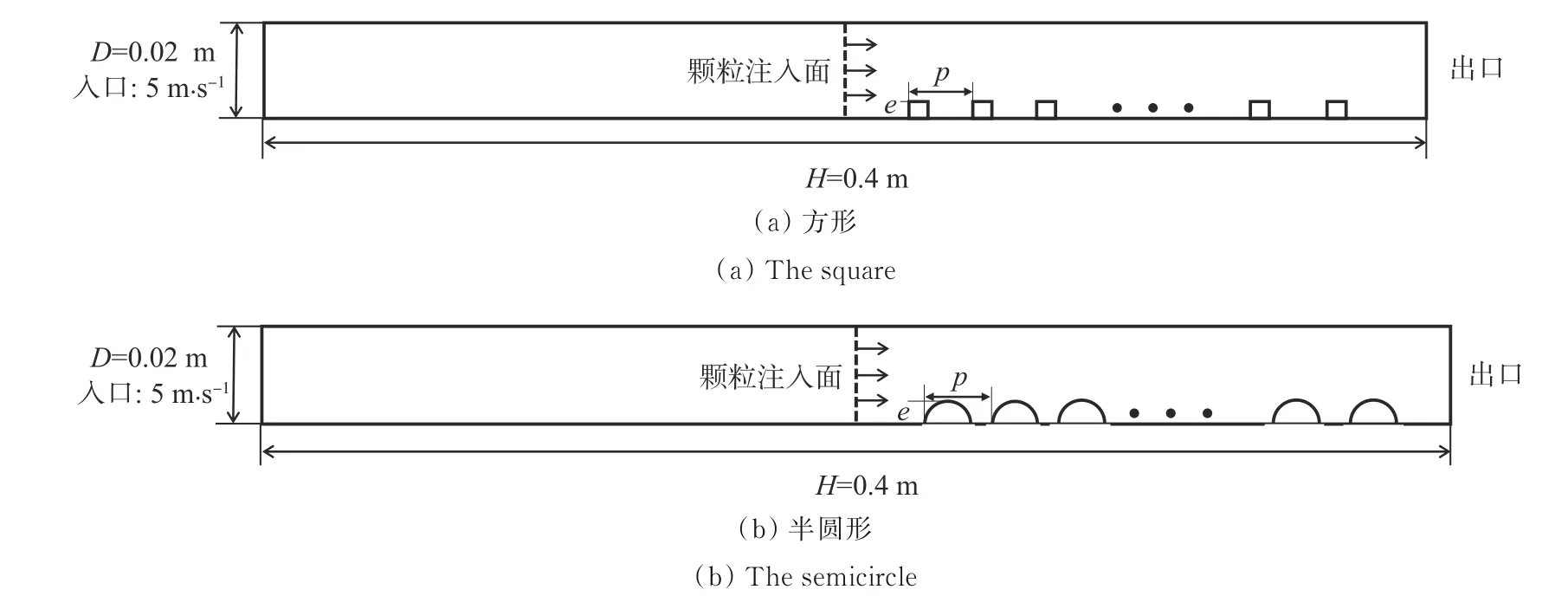
图1 粗糙元壁面计算域示意Fig.1 The schematic of ribbed ducts

2 研究模型与数值方法

2.1 控制方程

假设空气为常物性、不可压缩，RSM控制方程为

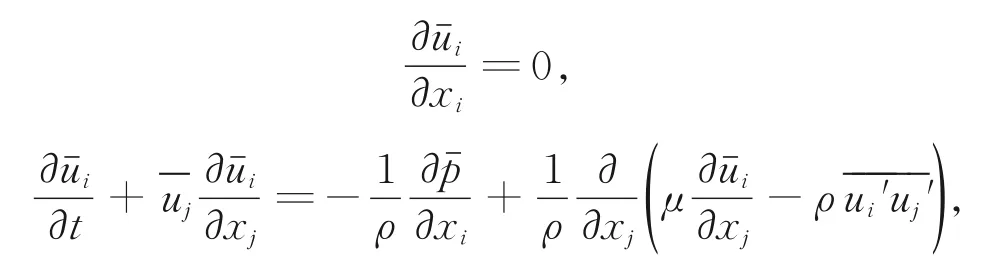
其中，和分别为空气平均速度和平均压强。雷诺应力项′可用以下方程表述：

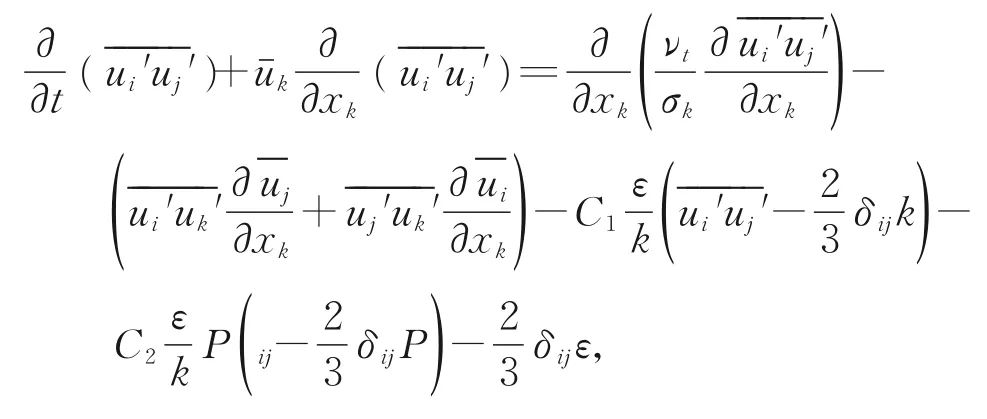
其中，νt为空气湍流黏度，σk，C1，C2为经验常数，取值分别为1.0，1.8，0.6。湍流耗散率ε的输运方程为

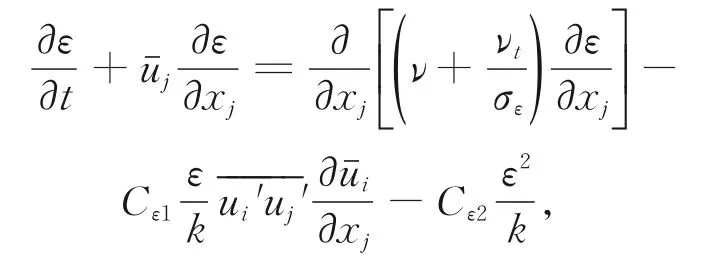
其中，σε，Cε1，Cε2为经验常数，取值分别为1.30，1.44，1.92。

由于颗粒浓度偏低，可将颗粒视为离散相，采用拉格朗日法求解离散相的运动轨迹。假设颗粒为球形颗粒，不考虑颗粒的旋转、颗粒间作用及颗粒对流场的耦合作用，仅考虑流体对颗粒的单向耦合。同时，主要考虑曳力、重力与浮力、萨夫曼升力对颗粒的影响，结合离散相模型（DPM），求解颗粒运动特性。离散相模型控制方程为

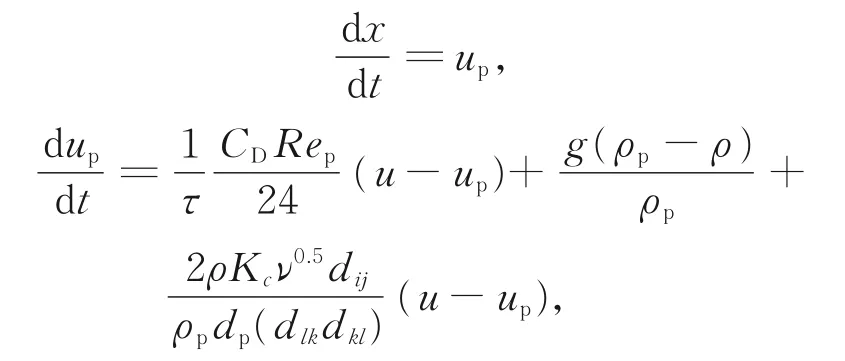
其中，Kc为系数，值为2.594，CD为曳力系数：

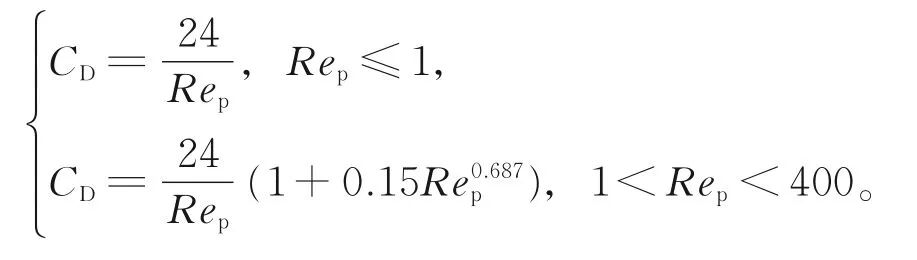
式中，Rep为颗粒雷诺数，Rep=为空气运动黏度。

2.2 颗粒沉积模型

BRACH等［13］在JKR理论的基础上，通过实验总结了半经验反弹速度，并将其称为颗粒沉积临界速度Vcr，用以判断颗粒是否沉积。当颗粒撞击壁面的法向速度Vn小于临界速度Vcr时，认为颗粒沉积；反之，认为颗粒与壁面作用后反弹，以一定速度汇入空气中继续运动。临界速度Vcr表达式为

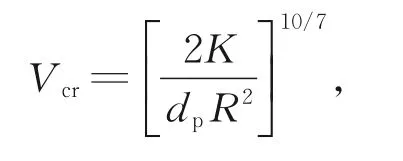
其中，有效刚度参数

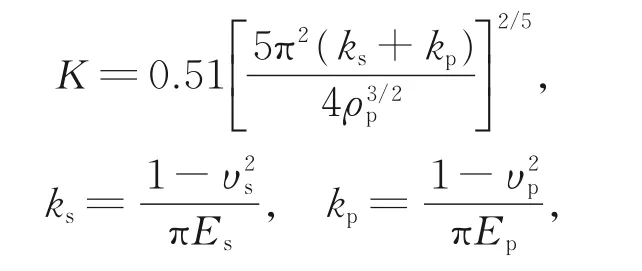
Es和Ep分别是壁面与颗粒的杨氏模量，υs和υp分别为壁面与颗粒的泊松比，dp和ρp分别为颗粒的粒径与密度，R为颗粒运动恢复系数，取R=0.9。

2.3 算例设置

以5 m·s-1的速度流入，自由流出；空气在壁面运动采用无滑移边界条件。空气运动黏度ν=1.48×10-5m2·s-1，密度ρ=1.225 kg·m-3。颗粒密度为ρp=2 450 kg·m-3，杨氏模量为192 GPa，泊松比为0.13。壁面材料用不锈钢，其杨氏模量为215 GPa，泊松比为0.28。为了消除入口效应对颗粒运动的影响，保证湍流充分发展，在H=0.2 m处释放45 000个颗粒进行追踪。通过ANSYS Fluent 18.0自定义函数（UDF）实现颗粒沉积模型。

3 结果与讨论

3.1 模型验证

为验证颗粒沉积模型在粗糙元壁面上运动的正确性，进行了流场与颗粒沉积特性两方面验证。选取X=150 mm的截面进行流场验证，流场结果与KIM等［20］的DNS流场数据及LU等［8］的RSM流场数据吻合较好（图2），获取了准确的流场信息，包括流场无量纲速度和高度：

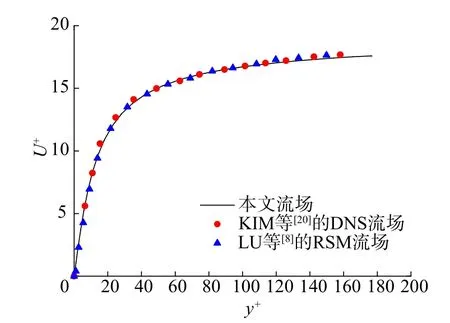
图2 X=150 mm处流场验证Fig.2 Air flow verification when X=150 mm

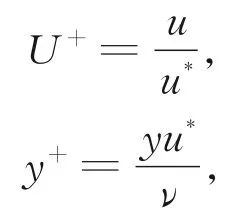
其中，U+为流场无量纲速度，y+为流场无量纲高度，u为当地流场速度，u*为摩擦速度，y为距离壁面的高度。

此外，分析了当e/D=0.1，p/e=8时，不同无量纲松弛时间τ+下的颗粒沉积速度Vd，并与LU等［8］的模拟结果进行对比，结果如图3所示。由图3可知，颗粒沉积速度整体趋势一致，但当颗粒粒径为1 μm时误差较大，这由未对近壁面处的湍流脉动进行修正造成。当颗粒粒径为2～10 μm时，本文结果与LU等［8］的结果较吻合，因此，可以用此积尘模型研究半圆形粗糙元壁面的颗粒沉积特性。τ+和Vd的表达式分别为

图3 颗粒沉积模型验证Fig.3 Particle deposition model verification

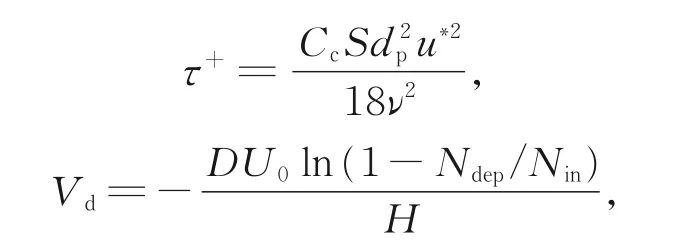
其中，Cc为科灵汉姆修正系数，S为颗粒与空气密度之比，dp为颗粒粒径，Ndep为颗粒沉积数量，Nin为进入计算域的颗粒数量。

3.2 空气流场分析

本研究中的颗粒粒径为1～10 μm，且仅考虑流场对颗粒的单向耦合作用。流场分析对于颗粒沉积研究起至关重要的作用。图4为方形和半圆形2种粗糙元在e/D=0.1，p/e=8时的流场分析结果。X和Y分别为二维计算域的横、纵坐标。由于粗糙元壁面流道变窄，空气流场加速，且空气在经过第一个粗糙元后，方形粗糙元壁面比半圆形粗糙元壁面加速明显。与光滑的上壁面相比，2种粗糙元导致边界层变厚，且下壁面的边界层呈波浪式。

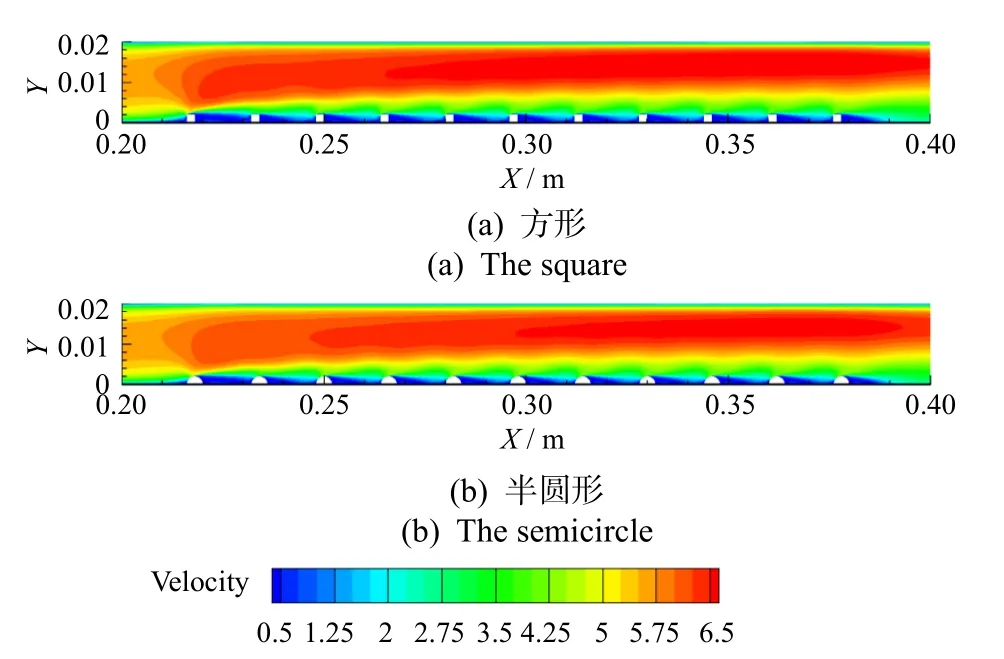
图4 2种粗糙元壁面速度分布Fig.4 Velocity distribution in two ribbed ducts

图5展示了2种粗糙元附近流场矢量图与流线图。当流体流经方形粗糙元壁面时，流场速度立刻增大，而当流体经过半圆形粗糙元壁面时，流场速度在经过半圆形粗糙元壁面顶点后才开始增大。这是由于空气在经过半圆形粗糙元壁面时紧贴半圆表面流动，且流体流经的横截面面积未发生突变。

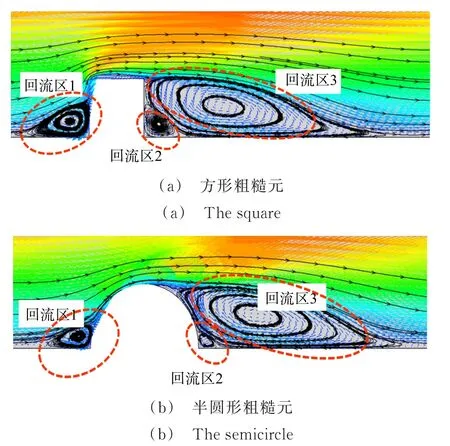
图5 2种粗糙元附近流场矢量图与流线图Fig.5 Vector and streamline diagram near two rough elements

空气在绕过粗糙元后，2种粗糙元的背风面均形成一大一小2个回流区，同时粗糙元的迎风面前端也形成一个回流区。背风面几何形状使得半圆形粗糙元回流区2的区域面积略小于方形粗糙元。同样，空气的附壁流动导致半圆形粗糙元回流区1的区域面积小于方形粗糙元。2种粗糙元回流区3的区域面积大致相同。回流区不同不仅使颗粒停留时间出现差异，也导致湍流耗散、湍动能等产生差异。

图6为7种算例下2种粗糙元壁面附近湍动能的分布。不同粗糙元参数下粗糙元壁面的湍动能差异较大。相比半圆形粗糙元壁面，方形粗糙元壁面的突变使得空气扰动增强（图5），因此同参数下的方形粗糙元附近空气的湍动能更大。不同粗糙元高度会引起不同的空气扰动，从而引起湍动能差异。在算例6中，当粗糙元的e/D=0.2时，其在所有算例中粗糙元高度最大，湍动能最大，壁面附近的最大湍动能达2.8 m2·s-2，而当e/D=0.02时，由于粗糙元高度较低，对流场扰动不明显，未产生很大湍流效应，其附近湍动能最大仅为0.9 m2·s-2。另外，湍动能对颗粒沉积特性有促进作用，因此需要探究粗糙元参数对颗粒沉积特性的影响。

图6 2种粗糙元附近湍动能分布（上方为方形粗糙元，下方为半圆形粗糙元）Fig.6 The distribution of turbulent kinetic energy near two rough elements（the upper is square，the lower is semicircle）

3.3 半圆形粗糙元与方形粗糙元颗粒沉积特性对比

图7展示的为半圆形粗糙元与方形粗糙元在不同颗粒无量纲松弛时间τ+下颗粒沉积速度的对比。可知，2种粗糙元在不同高度与间距下颗粒沉积速度呈现的规律一致，在2种粗糙元壁面上，颗粒沉积速度总体上均随颗粒无量纲松弛时间的增大而增大，而当颗粒无量纲时间大于10时，颗粒沉积速度略有下降。这是由于在颗粒无量纲松弛时间为0.1＜τ+＜10时，颗粒受湍流涡作用影响较大［21］，大量颗粒被夹带进入湍流涡，又由于颗粒的惯性很小，难以逃离湍流涡的束缚，使得颗粒与壁面的碰撞大大增加，导致颗粒沉积现象严重。当τ+＞10时，颗粒属于大粒径［22］，惯性力占主导作用，颗粒沉积速度Vd保持稳定。由于本研究中颗粒范围较小，τ+＞10的颗粒较少，此处略有下降可以认为颗粒沉积速度处于稳定状态。

在同一粗糙元参数下，半圆形粗糙元颗粒沉积速度Vd均低于方形粗糙元。由于半圆形粗糙元的回流区较小，颗粒进入回流区的概率较低。此外，半圆形粗糙元的外形结构与来流的垂直性不及方形粗糙元，迎风面不能拦截更多的颗粒，所以相比方形粗糙元壁面，半圆形粗糙元壁面没有出现很严重的颗粒沉积现象。

3.4 半圆形粗糙元间距与高度对颗粒沉积特性的影响

图7（a）展示了当p/e=8时e/D对颗粒沉积特性的影响。当e/D=0.02时，颗粒沉积速度Vd最小且变化较明显。这是因为粗糙元的高度较小，拦截颗粒运动的效率较低，迎风面与壁面上的颗粒沉积数量都较小，且小尺寸粗糙元对气流的扰动较小，其附近不会引起较大的湍动能，导致受湍流影响较大的小颗粒跟随空气流出计算域，未在粗糙元壁面沉积。而当e/D=0.05，0.10，0.20时，颗粒沉积速度为0.04～0.10 m·s-1，变化不大。

图7（b）展示了当e/D=0.05时不同p/e下颗粒沉积速度的变化。当p/e=3时，受湍流影响较大的小粒径在单板壁面沉积较少，而大颗粒受惯性力沉积机制的影响，与其他粗糙元参数的沉积量级一致，使颗粒沉积速度范围较大。在算例4中，p/e=3，与拥有3个回流区的其他算例不同的是，虽然算例4的粗糙元引起了较大的湍动能，但算例4中相邻2个粗糙元的间隙较小，仅形成了一个大的回流区，颗粒难以向壁面方向运动。另外，本文其他半圆形粗糙元参数下颗粒沉积速度变化不大，这与LU等［8］研究同粒径方形粗糙元颗粒沉积速度的沉积特性一致。

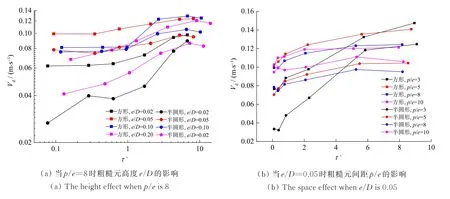
图7 2种粗糙元在不同颗粒无量纲松弛时间下的沉积速度对比Fig.7 Velocity distribution with different particle dimensionless relaxation time

3.5 半圆形粗糙元迎风面上的颗粒沉积分布特性分析

图8展示了半圆形粗糙元在5种不同粒径下的颗粒沉积分布特性，横坐标X表示计算域的位置，纵坐标表示颗粒沉积数量。由图8可知，将颗粒从X=0.20 m处释放，其在第一个粗糙元的迎风面大量沉积，出现颗粒沉积的峰值，且在下游的每个粗糙元迎风面上均出现峰值。这主要由粗糙元凸起的拦截作用造成，使大部分颗粒在粗糙元的迎风面沉积。而算例4与算例7颗粒沉积峰值不明显的主要原因是粗糙元的e/D与p/e较小。算例7中，较小的粗糙元不仅颗粒拦截效率较低，而且对流场扰动较小，粗糙元附近湍动能不大，从而导致分峰不明显。在算例4中，p/e=3，相邻2个粗糙元之间的空隙仅为e。因此，距离较近导致分峰不明显。

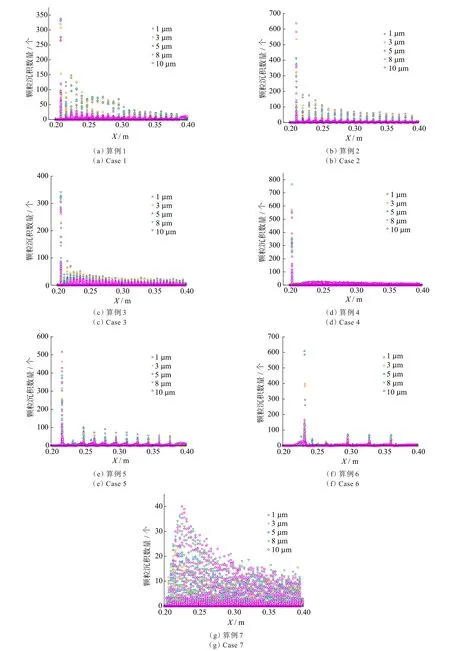
图8 在不同粗糙元参数下半圆形粗糙元壁面的颗粒沉积分布Fig.8 Distribution of particles deposition on the wall with different roughness parameters

另外，e/D很好地描述了壁面的相对粗糙度。由图7可知，粗糙元引起的流场扰动会影响湍流性质，从而对颗粒沉积产生影响。在算例7中，e/D=0.02，除了相对粗糙度较小引起颗粒的低拦截效率外，低粗糙度引起的低湍动能同样对颗粒沉积产生影响。从图6算例7的流场湍动能分布可以发现，流场湍动能的范围均较小，颗粒沉积效率较低，导致相邻2个粗糙元之间的颗粒沉积变化不大，形成的颗粒沉积峰不明显。算例4虽然有较大的粗糙元高度，粗糙元壁面附近也引起了较大的湍动能，但并没有导致较高的颗粒沉积数量。这是由于p/e较小，导致相邻2个粗糙元之间只有一个回流区，颗粒难以进入，大多数颗粒随空气流出计算域，导致粗糙元间的颗粒沉积数量不高，从而出现分峰不明显的现象。

颗粒在第1个粗糙元迎风面大量沉积后，在第2个粗糙元迎风面上的沉积却大幅下降。其原因是，一方面，第2个粗糙元附近的流场受粗糙元的影响较小（如图5所示），边界层增长尚不大；另一方面，大部分颗粒被第1个粗糙元拦截沉积，导致第2个粗糙元的拦截沉积数量不大。同时，当X=0.3 m时，流场边界层增长与湍动能开始趋于稳定，之后颗粒沉积数量也达到稳定状态，基本不变。