基于近场散射模型的超低空目标雷达回波模拟

王 童, 童创明, 王宜进, 刘 杰

(1. 空军工程大学防空反导学院, 陕西 西安 710051;2. 中国人民解放军94782部队, 浙江 杭州 310021)

0 引 言

由于来自环境杂波以及目标与环境之间多径回波的干扰,雷达很难实现对地海面背景中目标的准确探测。特别是对于弹载雷达导引头末制导阶段,由于距离目标较近,其电磁波散射与传播机理明显不同于远场条件,这就决定了其雷达回波的特殊性与复杂性。当前,单纯研究目标与环境的电磁散射特征,已无法满足对复杂场景雷达特性分析的需求。在精细电磁散射模型基础上,直接模拟复杂场景的雷达回波信号,具有清晰直观的优势,成为近些年雷达仿真研究的热点。

目前应用最广泛的近场散射问题研究思路是:当雷达辐射天线距离目标较近,但相对距离仍远大于雷达波长以及天线尺寸时,目标表面的入射电磁场仍可认为处于雷达天线的远场“辐射”区域,然而照射目标的电磁波不再视为平行,因此可以将入射波近似为球面波而非平面波。对于接收天线,目标位于近区会使得分析十分复杂,但对于目标局部的每一个小面元而言,其与接收天线又符合远场条件。在近些年近场电磁方法研究中,基于物理光学(physical optics, PO)与等效电磁流法(method of equivalent current, MEC)的改进方法得到了较大关注。该类方法简单高效,十分适用于计算量巨大的回波模拟。

电磁散射特性并不是雷达回波信号的直接反映,实际雷达接收的回波信号是目标或环境散射数据与雷达发射信号卷积后的结果。将复杂电磁模型引入雷达信号模型已得到较大关注,文献[16-18]借助电磁模型研究了海杂波特性,文献[19-25]研究了环境及其表面目标的多普勒回波特性,文献[26-29]则对环境的极化合成孔径雷达回波进行了仿真。这些研究都基于电磁计算方法完成了回波特性的仿真分析,但是发射信号过于简单,均为简单的正弦电磁波,缺乏对雷达及场景参数的考虑,同时均未考虑近场条件下的回波特性。从当前研究看,对于复杂场景的近区雷达回波仿真研究明显不足。

针对当前超低空近区目标雷达回波仿真研究的缺乏,本文在PO与等效电磁流近场电磁散射模型基础上,对目标、环境以及多径回波进行模拟仿真,对电磁模型的有效性进行了验证,分析了回波信号的特点。

1 近场电磁模型

1.1 目标近场模型

当辐射天线与目标距离较近时,入射波为球面波,远场雷达散射截面(radar cross section, RCS)的定义不再适用,这里需要重新定义近场RCS为

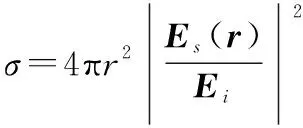
(1)

式中：不再趋于无穷。传统PO中远场计算主要是通过对格林函数的近似实现的,其中需满足

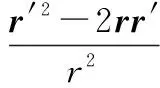
(2)

使式(2)成立存在两种情况,一种即距离→∞,另一种则为源点矢量′→。当→∞时,即所谓远场条件。所以对于采用PO计算近区散射场的情况,需寻求满足第二种条件的方法。使源点矢量′→,可以借助中间变量来实现。设目标表面某一点位置矢量为,场点与源点′距离为

=|-′|=|(-)-(′-)|=|-′|

(3)

式中：=-；′=′-。以代替式(2)中的,′代替′有：

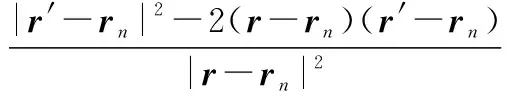
(4)

通过观察发现当′=时式(4)是成立的,即当′位于附近时,远场形式的PO是符合使用条件的,但表达式中的格林函数近似形式变为

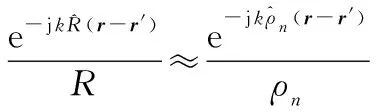
(5)

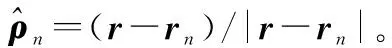
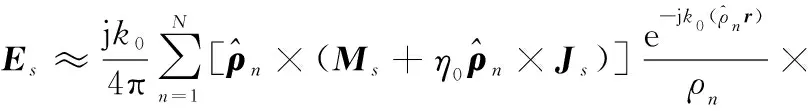
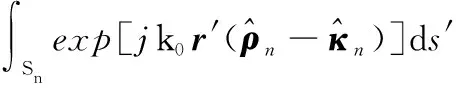
(6)

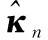
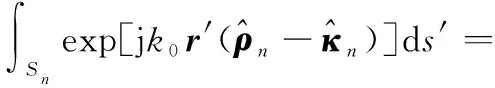
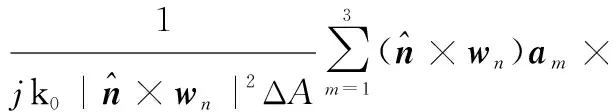
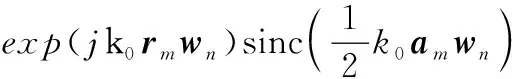
(7)

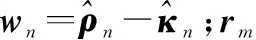
类似的近区散射场计算思想可以推广至MEC,对于边缘为C的劈边,其远区的边缘绕射场为

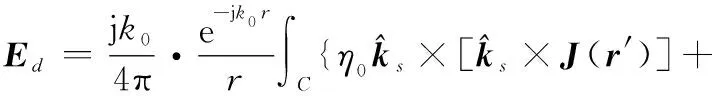
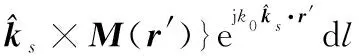
(8)

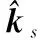
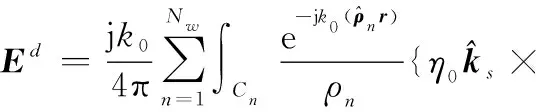
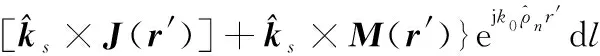
(9)

式中：为目标表面离散后的劈边个数,每一个边缘绕射源,是由棱边相邻的两个小三角面元组成。

需要特别指出的是目标近区散射场计算中,接收天线与目标上每个离散面元之间的距离是有限且不同的,这与远场认为距离是无穷远具有本质区别。

1.2 环境与多径近场模型

在计算环境的散射场时,近似认为粗糙面由一系列表面光滑的三角面元组成如图1中所示,即视粗糙面为二维扩展目标。通过蒙特卡罗法获得确定的粗糙表面后,则每一个面元的近区散射场可采用第11节计算目标的PO方法获得。在多径散射计算中,“四路径”模型因其简易高效的特点,在工程电磁仿真中得到了广泛的应用。

图1 粗糙表面面元散射示意图Fig.1 Sketch map of facet scattering for rough surface

如图2所示,第1条路径为目标的直接散射场,第2条路径为目标的散射场经环境镜面反射后的散射场,第3条路径为环境的镜面反射场照射到目标,然后经目标散射到雷达的场,第4条路径为环境镜面反射场经目标散射后再次由环境镜面反射到雷达的场。

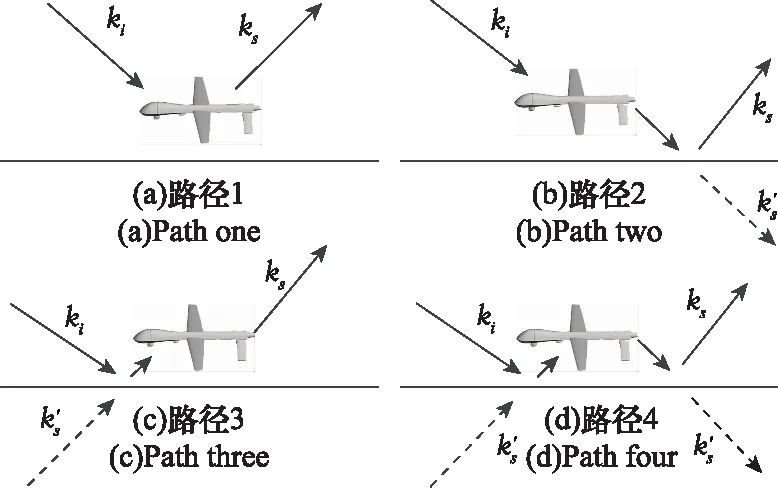
图2 “四路径”模型示意图Fig.2 Sketch map of four path model

后3条路径表示目标与环境的相互作用。按照“四路径”模型雷达接收的总场为

=++++

(10)

式中：为环境表面散射场；为目标散射场；,,分别对应路径2、3、4,也称为耦合场。在计算目标与环境的耦合场时,可以采用镜像原理,将目标与环境的二、三次散射等效为目标的双站散射,等效示意如图2所示。同时需注意,等效入射或散射方向上的场需乘以环境表面的反射系数,所以总场可以表示为

(11)

雷达距目标较远时,目标与多径散射均主要发生在天线主波内,入射波可视为平面波。在近区条件下,目标与附近环境表面的反射点很有可能不在雷达天线同一波束内,如图3所示。此时入射波不但不再是平面波,而且天线增益也不可以视为相同。

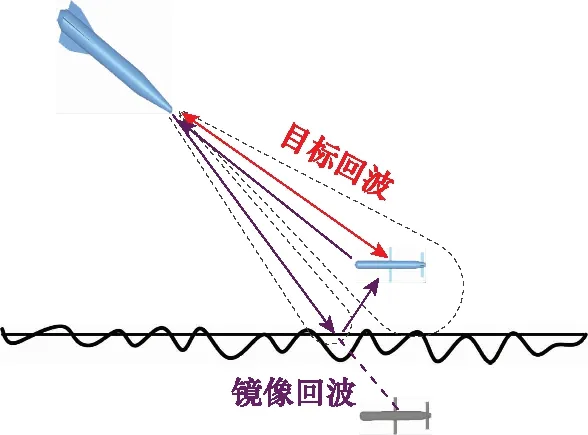
图3 近区多径回波信号示意图Fig.3 Sketch map of multipath echo signals in near zone

在近区条件下,目标近区双站散射的计算可采用上一节中的PO+MEC近场模型。但是对于反射点与目标不在同一天线波束内的情况,反射系数必须要考虑天线增益的加权,所以式(11)中的耦合场部分(路径2、3、4)改写为

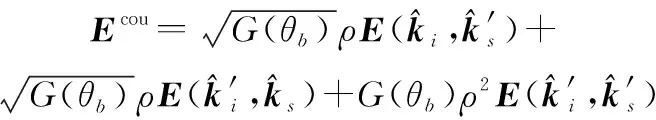
(12)

式中：为反射点-雷达连线与雷达中心波束(仿真中认为一直指向目标中心)的夹角；为天线增益。

在最初的四路径模型中,采用统菲涅尔反射系数。尽管微粗糙表面其散射能量主要集中在镜面反射方向,但仍存在较为明显的漫散射现象,通过引入了粗糙度反射因子可对传统菲涅尔反射系数,进行修正,其表达式为

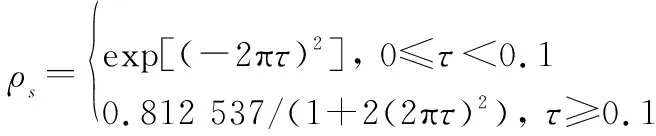
(13)

式中：=(cos),为表面高度起伏的均方根,为雷达波入射角,此时修正后的反射系数为

=,

(14)

本文采用一种基于高阶PO反射系数模型。对Stratton-Chu积分方程进行切平面近似,然后对散射场级数展开,得到反射系数为

=e-2cos(00+(02+
20-(00+ 00)cot)+…)

(15)

式中：为粗糙表面斜率的均方根；为极化方式；为反射系数的关于斜率的泰勒展开式系数。表面若为光滑,则00及00与菲涅尔反射系数相等。以垂直极化为例,式(15)中前几项的展开式系数为

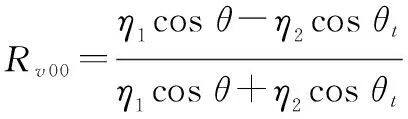
(16)

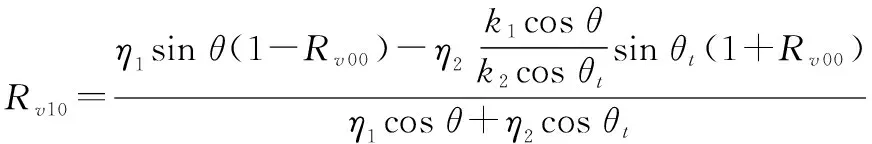
(17)

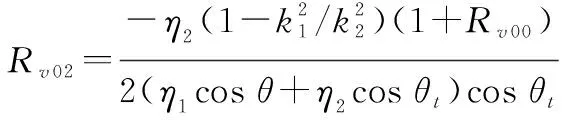
(18)

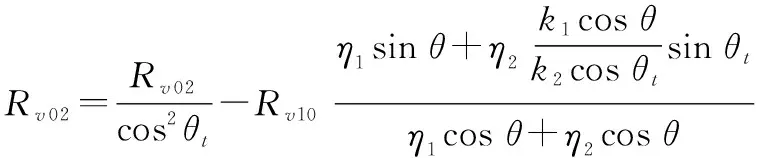
(19)

式中：与分别为粗糙面上层与下层介质的波数；与分别为入射角与投射角度且有sin=sin。将式(19)中的替换为,则相应的水平极化系数即可获得。

对于起伏并不十分剧烈的表面,式(15)中更高阶的贡献完全可以忽略,这里仅保留前两项,所以新的反射系数为

=(00+(02+20))

(20)

由式(20)可以发现,等式右边第一项为式(14)中的反射系数。

2 回波信号模型

目标与环境表面均可离散为众多小面元,每个面元的雷达回波可视为其中心点的回波,雷达接收的总回波即为所有照射区面元回波的矢量叠加。对于单站收发共用天线的雷达,时刻雷达接收单个面元的复信号为

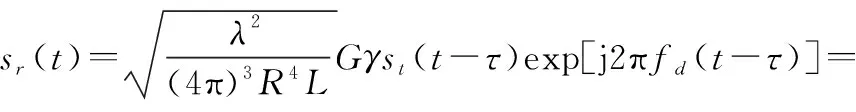
(21)

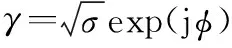
式(21)用来表示相对运动较慢目标的回波是足够的,但对于相对高速运动目标,该表达式是不够精确的。对第个脉冲回波进行零中频处理后,精确表示形式为

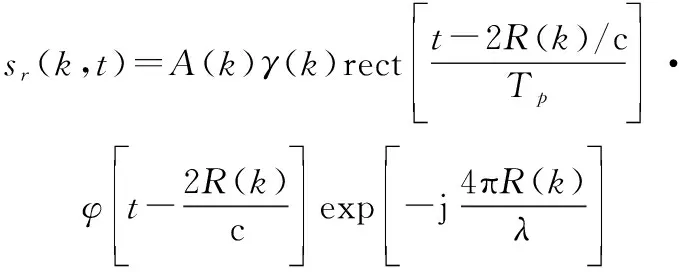
(22)

目标速度信息包含在()的变化中,对于由个面元组成的目标或环境,其总的回波表示为

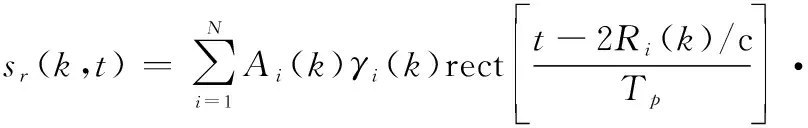
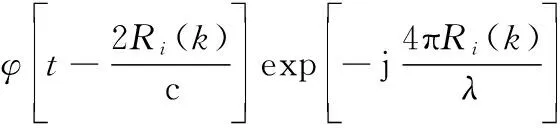
(23)

由式(23)可知,模拟雷达回波需要获知个脉冲时刻雷达照射区内所有面元的散射幅度()以及对应的相对距离()。()可由本文电磁散射模型计算获得。雷达参数以及与目标的相对运动规律确定后,()与()也都不难获得。当目标、环境以及多径回波的信号幅度与传播距离确定后,则超低空目标的雷达信号便可借助式(23)获得。

3 电磁模型的验证

目标散射计算采用的是基于PO与等效电磁流的近场电磁散射模型。同时通过面元模型与四路径模型,可分别将PO模型引入到了环境场与多径场的计算中。所以,验证目标、环境与多径散射场计算的有效性,其核心是验证PO与等效电磁流近场模型的有效性。同时根据式(12),对于多径场还需验证反射系数的有效性。

3.1 近场电磁模型有效性

首先利用文献[30]中的实测数据进行验证,目标为一圆柱,长30 cm,半径10 cm,则目标最大尺寸=36 cm。入射波频率为10 GHz,波长=3 cm。对距离目标0.3处的后向散射场进行仿真验证,结果如图4所示。

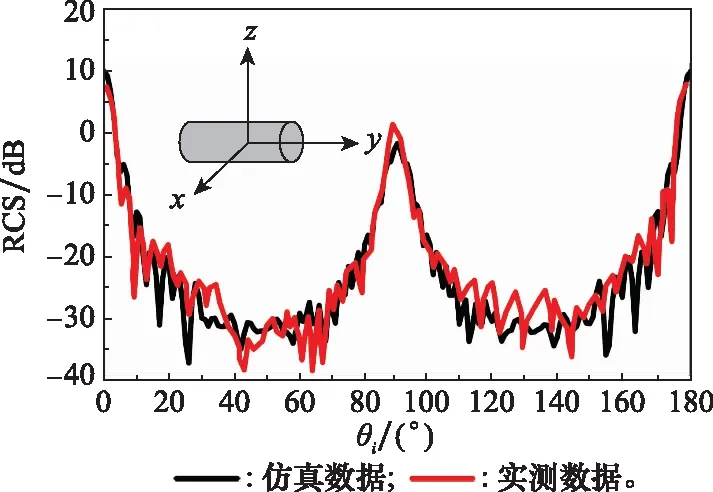
图4 目标近场电磁散射Fig.4 Near-field electromagnetic scattering of target

图4中两组数据对比显示,仿真数据与实测数据匹配较好,说明了基于改进PO+MEC计算电大尺寸目标近区散射场的有效性。再对天线与目标不同距离的近区散射场进行仿真验证,计算模型为一正方形平板,尺寸为10×10。PO在平面垂直方向的精度最高,所以计算数据为入射角为0°的后向散射场,验证数据则为采用矩量法计算获得的散射场,结果如图5所示。其中，横坐标为距离进行了归一化处理(除以1 m)并取常用对数后的结果。

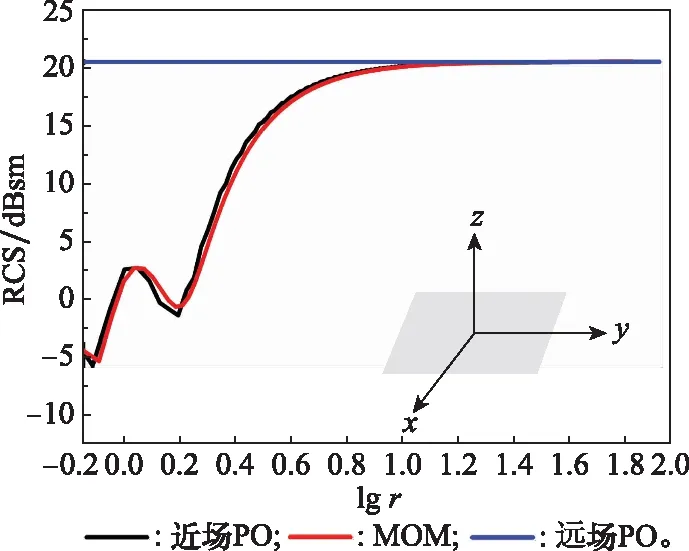
图5 散射场随距离变化规律Fig.5 Variation of scattering field with distance

图5中的结果显示,近场PO在0°入射角方向与矩量法的计算结果基本吻合,而远场PO的计算结果则与距离无关,在距离目标较近的范围内存在巨大误差。以上仿真结果表明,对于电大尺寸目标的近区散射场,改进的PO与MEC具有较好的计算精度。

3.2 反射系数有效性

反射系数的有效性主要借助文献[31]中的数据进行说明,图6为式(14)中的反射系数模型与式(20)中的反射系数模型以及干土的实测数据(来源于文献[31])的对比。其中，表面相对介电常数为=3.0-j0.0,可以发现当归一化的均方根高度=0515和表面斜率的均方根=0135时,垂直极化的布儒斯特角(散射场垂直极化极小值处)位于60°。图6(a)显示两种反射系数模型与实测数据拟合均较好。当=139,=0185时表面粗糙度显著增加,布儒斯特角位于57.5°。从图6(b)中可以发现,式(20)中的反射系数模型匹配效果更好,从而证明式(20)中的模型较传统反射系数模型更为合理有效。

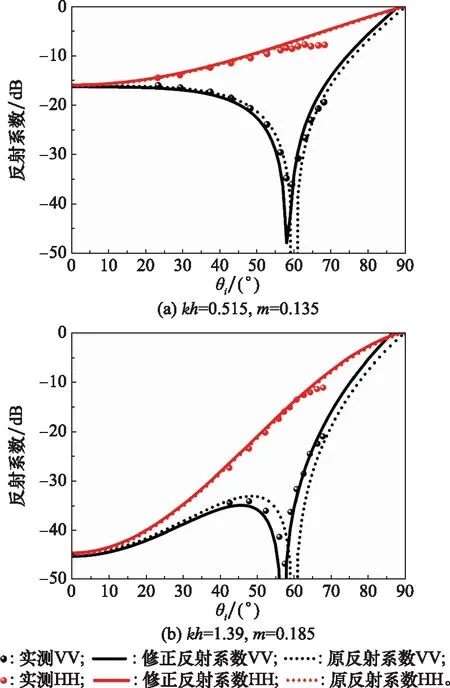
图6 反射系数与实测数据的对比Fig.6 Comparison of reflection coefficient between simulated and real data

4 雷达导引头近区回波仿真

以弹载雷达导引头对抗海面超低空目标为应用背景,对雷达回波进行仿真模拟。海面为一级海况,海面上方10 m处风速=1.2 m/s,海水相对介电常数为42.08-j39.45。导引头为脉冲多普勒体制,工作载频为16 GHz,与目标相距500 m,被拦截目标(如图3中所示)长5.56 m。导引头运动速度为730 m/s,目标飞行速度为200 m/s,距海面高20 m,仿真中简单认为雷达导引头与目标均平行于地面飞行。雷达天线主瓣半功率波束宽度为3°,第一旁瓣为-20 dB。

首先仿真分析“迎击状态”,即导引头与目标径直相向运动。照射波中心波束擦地角为15°,信号带宽为5 MHz,脉冲重复频率250 kHz,对512个脉冲的回波数据进行仿真,结果如图7所示。

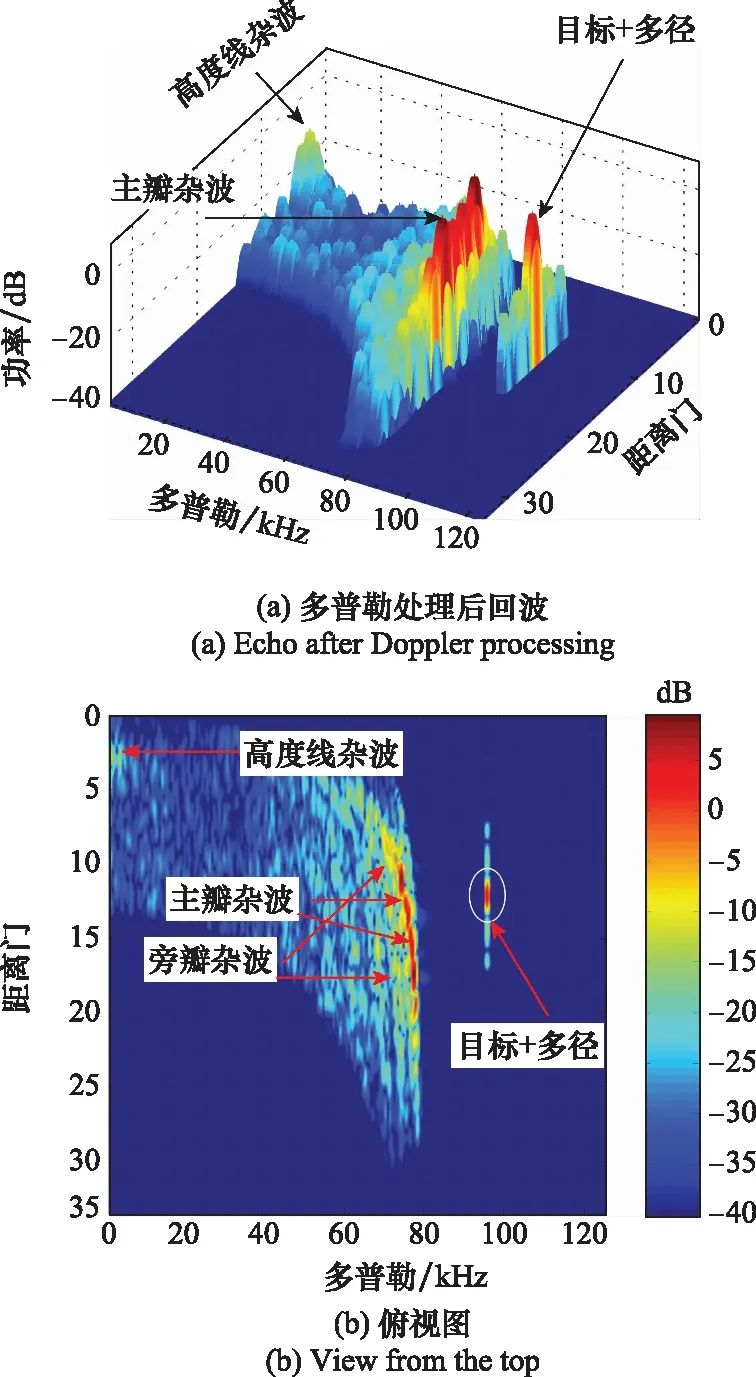
图7 近区超低空目标回波Fig.7 Echo of ultra-low altitude target in near zone

图7显示,近区情况下旁瓣杂波功率较强,尤其在距雷达较近(距离门数较小)的区域,旁瓣杂波尤为明显,在导引头正下方(距离门数最小,多普勒几乎为0)杂波最强,该处杂波即为高度线杂波。相比远区,雷达距目标较近时,旁瓣杂波效应增强了。由于处于迎击状态,导引头与目标相对多普勒较大,可与杂波在频域显著分离,但在追击状态下且目标散射截面较小同时,在多普勒维目标会落在旁瓣杂波区域,这就增加了目标信号的检测难度。图8为目标运动方向与雷达视线水平投影方向夹角=60°且背向导引头时的距离多普勒图。图8(b)结果显示,目标与多径回波处于强旁瓣杂波区域中,距离维与多普勒维均不易分离,旁瓣杂波对目标检测的影响明显增强。

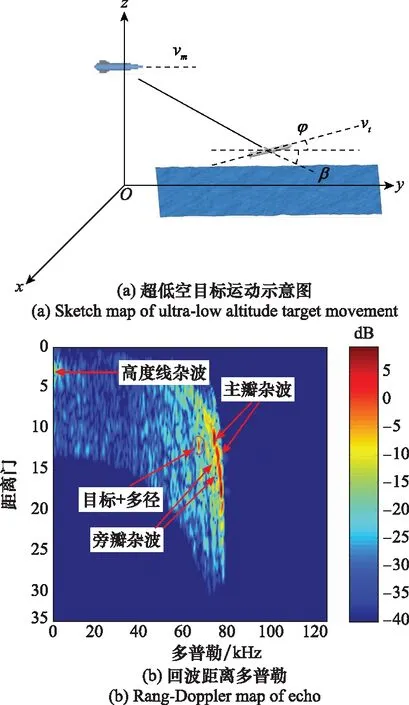
图8 近区超低空目标回波(φ=60°)Fig.8 Echo of ultra-low altitude target in near zone (φ=60°)

在雷达远区杂波的模拟中,通过提高信号带宽能够显著减小距离分辨单元内的杂波功率。在近区雷达回波仿真中,将发射信号带宽增加至50 MHz,目标运动方向与雷达视线水平投影方向夹角不变(=60°),计算得到回波信号的距离多普勒如图9所示。通过比较图8与图9的结果,可以发现目标与多径的回波功率峰值变化并不明显,但距离多普勒图显示的杂波尤其是旁瓣区域的杂波功率显著降低,目标信息相对更为突出。所以,通过增加信号带宽可以有效提高雷达导引头对近区强杂波背景中相对速度较小或者追击目标信杂比,提升目标检测性能。

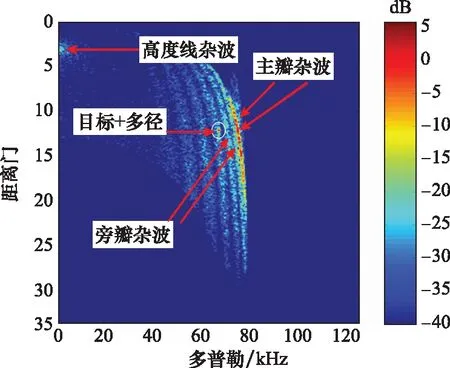
图9 发射信号带宽为50 MHz的近区超低空目标回波Fig.9 Echo of ultra-low altitude target in near zone with transmitting signal bandwidth 50 MHz

5 结 论

本文针对超低空近区目标复杂的电磁散射与传播机理,提出了一种基于近场电磁散射模型的雷达导引头回波模型。在对PO与等效电磁流法改进的基础上,完成目标近区散射场的计算。通过对粗糙面进行面元离散以及将“四路径”模型中多径散射等效为目标双站散射,从而将目标的近场散射模型引入到环境与多径散射场的计算中。在近场散射数据基础上,完成了近区超低空目标雷达回波信号建模。验证了电磁模型的有效性,模拟了海面超低空目标的雷达导引头回波。本文回波模型充分考虑了各种复杂电磁散射机理、雷达信号参数以及与目标相对运动状态的影响,将信号建模与散射计算进行了有效融合。仿真结果表现了近区超低空目标的强旁瓣杂波效应,以及信号带宽对回波结果的影响,显示了该信号模型在超低空近区目标雷达回波特性分析方面的直观、全面与可靠性。本文模型涵盖了超低空目标显著的多径回波效应,限于篇幅并未深入研究,下一步将对近区超低空目标的多径回波特性以及目标与多径回波的分离方法进行研究。