振动陀螺椭圆参数的离散滑模控制

郜中星, 彭 斌, 陈小炜, 张勇刚,*

(1. 哈尔滨工程大学物理与光电工程学院, 黑龙江 哈尔滨 150001;2. 哈尔滨工程大学智能科学与工程学院,黑龙江 哈尔滨 150001; 3. 陆军步兵学院石家庄校区军政训练系, 河北 石家庄 050083)

0 引 言

滑模变结构控制(简称为滑模控制)由苏联学者Utkin于1950年提出。作为一种非常受欢迎的非线性控制方法,滑模变结构控制在学术界得到了广泛的研究,并且由于微处理器技术的巨大进步,使得快速切换成为可能,从而使得滑模变结构控制成功地应用到了工业生产中[1]。滑模变结构控制获得巨大成功的关键还在于其自身拥有很多的优点,例如设计思路简单、速度快、鲁棒性强等[2-4]。因为越来越多的先进控制系统是由计算机控制实施的,离散滑模变结构控制逐渐成为滑模控制文献研究的热门话题[5-7]。

振动陀螺作为新一代陀螺仪,具有易于小型化、高精度、低成本、高可靠性、超高稳定性等优点[8-10],在远洋航海、深空探测、地质钻探等领域有着广阔的应用前景[11]。振动陀螺的控制策略关乎振动陀螺仪能否保持在谐振频率处以稳定的幅度振荡工作,这是振动陀螺仪正常工作的前提,其控制效果决定了陀螺仪精度的上限。

在振动陀螺的滑模控制研究方面,文献[12]讨论了将滑模控制运用于微机械(micro-electro-mechanical system, MEMS)陀螺仪过程中关于降低抖振、抑制不匹配干扰、扇区输入非线性的自适应补偿等方法,并通过仿真验证了所提策略的有效性和优越性。文献[13]将滑模控制应用在工作于力平衡模式的MEMS陀螺仪上,通过数值仿真结果验证了该控制器对于参数变动具有很好的鲁棒性,并且在阻尼和刚度不对称以及噪声存在条件下,该控制器仍能保证系统运动状态跟踪理想运动轨迹。文献[14]提出一种新型自适应分数阶滑模控制器,通过新的自适应律更新分数阶滑模控制器的增益,使得MEMS陀螺运动具有更高的追踪精度和更强的抗干扰性。文献[15]将径向基函数(radial basis function, RBF)神经网络与滑模控制结合,解决了MEMS陀螺系统不确定部分的自适应逼近,并且使用快速终端滑模控制,实现了系统状态有限时间收敛。文献[16]针对MEMS陀螺提出了一种快速自适应比例-积分(proportional-integral, PI)滑模控制策略,实现了快速稳定地跟随输入信号的目的。文献[17]提出了一种基于双环递归神经网络逼近器的MEMS陀螺分数阶非奇异终端滑模控制器,采用内循环和外循环提供反馈信号,以获得满意的逼近精度。值得注意的是,虽然目前国内外学者运用滑模控制结合自适应、分数阶微分、神经网络等方法对振动陀螺进行了研究[18],但主要集中在用连续滑模控制方法直接控制振动陀螺的运动状态,使之跟踪上一个假设的、幅值和频率恒定的理想运动轨迹,然后通过跟踪的快速性、准确性和鲁棒性等各方面指标评价滑模控制的效果[19-21],而这与实际中需要运用离散滑模控制,并且陀螺的谐振频率会受到干扰因素影响而产生变化有较大出入。

基于滑模控制现有的研究成果和存在的实际问题,本文提出从表征振动陀螺工作状态的椭圆参数出发,将离散滑模控制首次应用于振动陀螺的控制系统中,从而减小振动陀螺在全角模式下驻波进动角的漂移误差和标度因数误差。本文的结构安排如下:第1节介绍离散滑模控制的到达性条件,并选取恰当的离散滑模控制趋近律;第2节首先分析椭圆参数并选取主波振幅和正交波振幅作为控制对象,然后对控制对象进行了数学建模,最后结合趋近律和滑模面函数(切换函数)求取离散滑模控制律;第3节给出了比例-积分-微分(proportional-integral-derivative, PID)控制和离散滑模控制的仿真对比,仿真结果验证了离散滑模控制的优良特性。

1 离散滑模控制原理

1.1 离散滑模基本概念

当离散滑模控制施加于系统时,系统状态响应一般包括3种模态:趋近模态(reaching mode, RM)、滑动模态(sliding mode, SM)和稳定模态(steady-state mode, SS),如图1所示。

图1中有两种类型的离散系统状态运动轨迹,分别记为I和II。I型轨迹代表理想状态轨迹,II型轨迹代表了实际滑模控制系统的状态轨迹[22]。

需要注意地是,II型轨迹下系统状态为准滑动模态运动,在切换平面附近形成锯齿型的轨迹。通过观察该轨迹可知实际情况下的离散滑模控制系统状态轨迹应该有以下特点:

(1) 从任意的初始状态出发,状态轨迹单调地趋向切换平面并在有限时间内穿越;

(2) 一旦状态轨迹穿越了切换平面,之后的每一步都要穿越切换平面,围绕切换平面形成锯齿形轨迹:

(3) 每一步锯齿形状态轨迹的大小是非增的,并且保持在一个特定的准滑动模态带内。

如果离散滑模控制同时满足以上3个条件,就称之为满足了到达性条件[23]。

1.2 趋近律选取

在离散滑模控制系统的设计中,高为炳院士提出的趋近律设计方法是一种简单有效的方法[22, 24],其主要思想是先构造满足离散滑模到达性条件的趋近律,然后利用趋近律和所设计的切换函数求取离散滑模控制律。高为炳院士提出的离散指数趋近律如下所示:

s(k+1)-s(k)=-gTs(k)-εTsgn(s(k))

(1)

式中:g>0,ε>0,1-gT>0；T为采样周期；sgn(·)为符号函数。

基于式(1)设计的离散滑模控制系统具有误差快速收敛、系统抖振较小等优点,但由于等速趋近项-εTsgn(s(k))的增益为常数,使得系统状态最终不能趋于平衡点,而是围绕切换面s=0振荡。

为了有效地消除稳态时振荡,并且使系统状态兼具“向切换面渐近趋近”和“穿越切换面”两种特性,文献[6]提出一种改进的离散趋近律:

s(k+1)-s(k)=-gTs(k)-F|s(k)|Tsgn(s(k))

(2)

式中:g>0,1-gT>0；T为采样周期；

其中,Δ为切换带{x∈Rn||s(x)|<Δ}宽度；λ1和λ2满足如下条件:

(3)

利用式(2)所示的趋近律设计离散滑模控制器,不仅可以使得系统状态在有限时间内到达切换带内,而且系统状态进入切换带后将步步穿越切换面,并且抖振逐渐衰减至零。因此,本文选取式(2)作为离散滑模控制的趋近律。

文献[6]对趋近律(2)的到达性条件证明、趋近运动和滑模运动过程分析进行了充分的阐述,故这里不再重复说明。

值得注意的是,由式(2)可得

s(k+1)=(1-gT-FT)s(k)

(4)

调整λ1和λ2的取值大小可以改变切换函数s(k)变化的速度。其规律和影响效果如下:

(1)λ1越大,1-gT-λ1T越小,切换函数s(k)衰减地越快,系统状态进入切换带Δ越快,但会使得系统状态到达切换面时抖振越大;

(2)λ2越小,|1-gT-λ2T|越小,切换函数s(k)衰减地越快,系统状态趋近切换面越快(s(k)=0),但离散滑模控制律的抗干扰能力也越弱。

基于这些变化规律,可以为离散滑模控制的仿真调试提供指导。

2 模型建立与控制律求取

2.1 离散滑模控制参数分析

由文献[25]可知,振动陀螺运动模型可等价为一个质点在二维平面上的椭圆进动模型。将相隔45°的检测电极上的振动信号分别输入示波器的X、Y通道,可以观察到典型的李沙育图形,如图2所示。图2中X轴为0°检测电极轴方向,Y轴为45°检测电极轴方向,nθ为主波波腹轴与X轴的夹角,a为主波振幅,q为正交波振幅,φ0为质点运动的初始相位,ω为谐振子振动的角频率。参照文献[26]的方法,可以得到各椭圆参数的表达式如下。

(1) 主波振幅a:

(5)

主波振幅代表振动陀螺振动的幅度,陀螺正常工作时要求其保持为恒定值。

(2) 正交波振幅q:

(6)

正交波振幅反应了振动陀螺偏离理想工作状态的程度,理想情况下应将其抑制到0。

(3) 相位差δ:

(7)

相位差指的是参考信号发生器产生的参考信号与陀螺检测电极产生的电压信号之间的相位差,将其锁定到0°即完成了对振动陀螺的锁频和锁相工作,即振动陀螺保持在其谐振频率处振动。其中,E、Q、L由振动陀螺检测信号和参考信号经调制解调组合得到,其含义与文献[26]中一致,故不再赘述。

由以上分析可知,控制振动陀螺工作的椭圆参数有3个:主波振幅a、正交波振幅q和相位差δ。由于锁定相位差δ涉及因素较多、难度较大,并且在现行PID控制下也已经有了较高控制精度,恰恰主波振幅a和正交波振幅q仍有较大提升空间。进一步分析,借助文献[25]中的积分平均法,将振动陀螺非理想运动方程转化为椭圆参数方程[27],可得到关于驻波进动角θ的表达式:

(8)

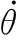
综上所述,在本文的离散滑模控制研究中,主波振幅和正交波振幅用离散滑模控制,相位差仍用之前相同参数的、经典的PID控制。

2.2 控制对象数学模型的建立

针对所控制的对象a和q建立数学模型,并写成状态方程的形式:

(9)

式中:Esmc和Qsmc分别代表幅值控制信号和正交控制信号。

为方便叙述,将式(9)记作:

(10)

由于rank([BABA2BA3B])=4,说明式(10)所描述的系统状态是完全可控的,即说明控制输入Esmc和Qsmc有能力将a和q控制到设定值[28]。

将式(10)用离散化公式进行离散化[29],得到如下形式的离散系统:

X(k+1)=ΦX(k)+ΓU(k)

(11)

式中:

2.3 离散滑模控制律求取

对跟踪问题,设计切换函数(滑模函数)为

S(k)=[sa(k);sq(k)]=CE(k)=C[Xd(k)-X(k)]

(12)

在本文设计的离散滑模控制中,a和q的切换函数分别为

(13)

(14)

为了保证对应的多项式p+c1和p+c2满足Hurwitz稳定,需要多项式p+c1=0和p+c2=0的特征值实数部分为负数,即要求

(15)

由式(12)和式(13)可得

S(k+1)=C[Xd(k+1)-X(k+1)]=
C[Xd(k+1)-ΦX(k)-ΓU(k)]

(16)

式中:Xd(k+1)为下一时刻的目标值。

在多输入问题下,式(2)所示的趋近律改写为

S(k+1)=(I-gT)S(k)-TFdiag(|S(k)|)sgn(S(k))

(17)

式中:diag(|S(k)|)表示以向量|S(k)|中的元素构造对角矩阵。

联立式(16)和式(17)可得离散滑模控制律:

U(k)=(CΓ)-1[CXd(k+1)-CΦX(k)-
(I-gT)S(k)+TFdiag(|S(k)|)sgn(S(k))]

(18)

3 模型搭建和仿真对比

3.1 仿真模型搭建

根据振动陀螺的非理想运动方程、位移至电压转换的检测原理、检测信号与参考信号的解调原理、椭圆参数的解算方法、控制输出的调制原理以及静电力的驱动原理[30-32],分别搭建相应的Simulink模块,互联之后组成振动陀螺的仿真平台如图3所示,图中以顺序序号1～6依次标出所搭建的模块。仿真模型中的振动陀螺工作在全角(速率积分)模式下,即驻波进动角可以直接表征外界的转动角度。

离散滑模控制或PID控制方法可在图3中编号5所示的控制输出调制模块内搭建实现。为了后续能更方便地将仿真中离散滑模控制律移植到实际工程中应用,离散滑模控制使用自定义的通用函数模块且以编程的方式实现。考虑实际情况中驱动信号比检测信号的幅值通常大2个数量级以上,因此驱动信号与检测信号在实际的电路中会存在串扰问题。当扰动较大时,甚至会导致振动陀螺起振时的锁频失败。为了使仿真更接近实际情况,在图3中编号为2的检测模块和编号为6的驱动模块内加入了信号串扰的模型。

为了验证离散滑模控制的有效性,分别选取静止0°/s和100°/s旋转输入2种情况进行仿真对比实验。

3.2 静止条件下仿真

设置外界输入转速为0°/s,目标值矩阵Xd=[40 000;0;0;0]。

使用PID控制时,PID的参数选取如下:

Pa=30
Ia=1
Pq=1 000
Iq=1
Pf=3 000
If=1 000

需要说明的是,选取上述PID参数的依据是仿真程序在调试过程中抗串扰效果最好。而离散滑模控制可以通过控制量的切换使系统状态在受到干扰时具有强鲁棒性,因此能更好地降低串扰带来的影响。

当对主波振幅a和正交波振幅q使用离散滑模控制时,控制律式(18)中各参数的取值如下:

c1=c2=30

Δ=0.5

其中:

其余参数与PID控制仿真情况下设置一致。将这2种控制方法得到的仿真结果放置在同一张图中对比,如图4和图5所示,图中蓝色实线表示PID控制的结果,红色实线表示离散滑模控制的结果,黑色实线表示理论的驻波进动角度。

从图4可得到:

(1) PID控制作用下,主波振幅a在0.4 s后进入振荡阶段,振荡范围为40 023～40 024 LSB,10 s后振荡范围变为40 017～40 018 LSB,并有逐渐减少的趋势;正交波振幅q在0.1 s后进入固定幅值范围振荡,振荡范围为0.9～1.1,取整后结果为1 LSB;相位差δ在5 s后进入固定幅值范围振荡,振荡范围为0.011 1°～0.011 3°。

(2) 离散滑模控制作用下,主波振幅a以更快的速度跟踪上目标值,a可在0.1 s后进入固定幅值范围振荡,振荡范围为39 999～40 000 LSB;正交波振幅q跟踪速度下降,在0.4 s后进入固定幅值范围振荡,振荡范围为0.1～0.4,取整后为0 LSB;相位差δ在5 s后进入固定幅值范围振荡,振荡范围同样为0.011 1°～0.011 3°。

3.3 旋转条件下仿真

设定外界输入转速为100°/s,振动陀螺进动因子γ为0.27。用第3.2节同样的PID参数、离散滑模控制参数和目标值矩阵,得到仿真结果如图6和图7所示。

从图6中可得到:

(1) PID控制下,主波振幅a可在0.4 s后进入固定幅值范围振荡,振荡范围为40 023～40 024 LSB,10 s后振荡范围变为40 017～40 018 LSB,并有逐渐减少的趋势;正交波振幅q在0.1 s后进入固定幅值范围振荡,振荡范围为-2～2 LSB;相位差δ在4 s后进入固定幅值范围振荡,振荡范围为0.008°～0.014°。

(2) 离散滑模控制下,同样实现了主波振幅a更快速度地跟踪目标值,a可在0.1 s后进入固定幅值范围振荡,振荡范围为39 999～40 000 LSB;正交波振幅q跟踪速度仍然是逊色于PID控制,在0.2 s后进入固定幅值范围振荡,但跟踪精度有所提升,振荡范围为-1～1 LSB;相位差δ在4 s后进入固定幅值范围振荡,振荡范围同样为0.008°～0.014°。

4 结 论

本文提出了将离散滑模控制引入到振动陀螺椭圆参数的控制系统中,用来控制主波振幅和正交波振幅,提高了主波振幅和正交波振幅的跟踪精度,进而减小了振动陀螺在全角模式下驻波进动角的漂移误差和标度因数误差。从10 s内的PID控制与离散滑模控制的仿真结果对比可知:① 0°/s静止条件下,主波振幅a误差减小了16 LSB;正交波振幅q误差减小了1 LSB;振动陀螺的角度漂移速率减小了0.36°/h。② 100°/s旋转输入条件下,主波振幅a误差减小了16 LSB;正交波振幅q误差减小了1 LSB;标度因数误差减小了5 ppm。仿真结果体现了离散滑模控制的鲁棒性和快速收敛性。

本文基于振动陀螺得到的研究成果可广泛应用到半球谐振陀螺和MEMS陀螺等惯性传感器的研发与设计中,从而有效提升陀螺传感器的性能水平。