基于卡尔曼滤波器的半捷联导引头控制系统设计

韩宇萌,贾晓洪

(中国空空导弹研究院， 河南 洛阳 471009)

在现代战争中，精确制导武器已成为最主要和最有效的攻防手段，红外制导空空导弹由于具有制导精度高、目标识别能力强、隐蔽性好等优点，成为空战近距格斗不可或缺的精确制导武器[1]。近距格斗中红外导引头的主要作用是对目标进行自主搜索、自动识别、快速捕获和精确跟踪。目前红外型空空导弹已经发展到第四代，以滚仰式两轴框架结构和红外成像制导技术为标志，具有较强的目标识别能力和较高的制导精度。滚仰式两轴框架结构减小了导引头的体积，增大了导引头的跟踪场和随动范围。其小型化对改进导弹气动性能、提高射程具有重要的现实意义，大跟踪场和随动范围对扩大发射区实现越肩跟踪、降低载机机动占位等方面具有重要的现实意义[2-3]。滚仰式两轴半捷联导引头是第四代红外空空导弹的理想选择，美国研制的AIM-9X是其中的典型代表。

1 导引头控制现状分析

随着光电对抗技术的不断发展，在现代战争中，没有人工干扰的净空作战条件已经不复存在。红外空空导弹在锁定并攻击目标的过程中，各种红外有源干扰和目标逃逸相互交织，对红外导引头目标识别和稳定跟踪造成严重影响[1,4]。同时，近距格斗中导弹高速飞行时的大过载、高机动使得弹体姿态处在复杂变化中，再加上导弹外部气流的扰动，对导引头的目标跟踪和稳定控制造成严重影响。为了提高导引头控制系统的动态响应性能和跟踪精度，国内外学者进行了大量的研究。目前，导引头控制器设计大部分应用的是传统的PID控制算法[5]。PID控制器结构简单，对信号具有较好的控制作用，能使系统快速收敛到平稳状态，应用广泛。但PID控制效果依赖于模型，对控制扰动和噪声的处理能力不足，其控制器参数的选择对控制效果影响较大。为了提高导引头稳定平台的抗扰动能力和跟踪精度，诸多控制算法被应用于导引头控制系统中。如滑模控制方法被应用到导引头控制器设计中，它能够有效隔离弹体扰动，提高导引头的跟踪精度和控制鲁棒性[6-8]。采用神经网络的导引头控制策略，一般是通过对控制系统性能的自适应学习，实现PID控制器参数的最佳组合从而得到理想的控制效果，但这种神经网络自适应学习控制策略，其参数整定过程繁琐、算法复杂，实际应用中计算的实时性难以满足要求[9]。

卡尔曼滤波对控制干扰和测量噪声具有良好的滤波作用[10]，本文针对滚仰式半捷联导引头提出了一种基于目标状态估计的卡尔曼滤波方法应用于导引头控制，该方法结合了卡尔曼滤波器在滤除干扰噪声方面的良好性能，能够使滚仰式半捷联导引头在外部扰动和系统噪声的作用下保持对运动目标的精确跟踪。

2 导引头控制原理

滚仰式半捷联导引头具有滚转和俯仰两个自由度，其光学系统安装在稳定平台框架上，稳定平台内外框架在各框架力矩电机驱动下可绕相应框架轴转动[11]。导引头控制系统在设计时，首先根据稳定平台的外形尺寸和性能要求，制定系统的基本控制方案，然后选择系统主要元器件，最后建立数学模型分析系统动态响应，并根据期望的性能指标设计调节器。稳定平台由台体、传动机构、力矩电机、驱动功放、校正网络、角度传感器、角速度传感器等构成[12-13]。其控制回路多采用位置-速度双回路控制系统，其中位置回路主要用来提高控制系统的精度，速度回路主要用来减小控制系统的超调量，改善回路的动态性能，以满足系统的稳态和动态要求。滚仰式半捷联导引头控制原理框图如图1。

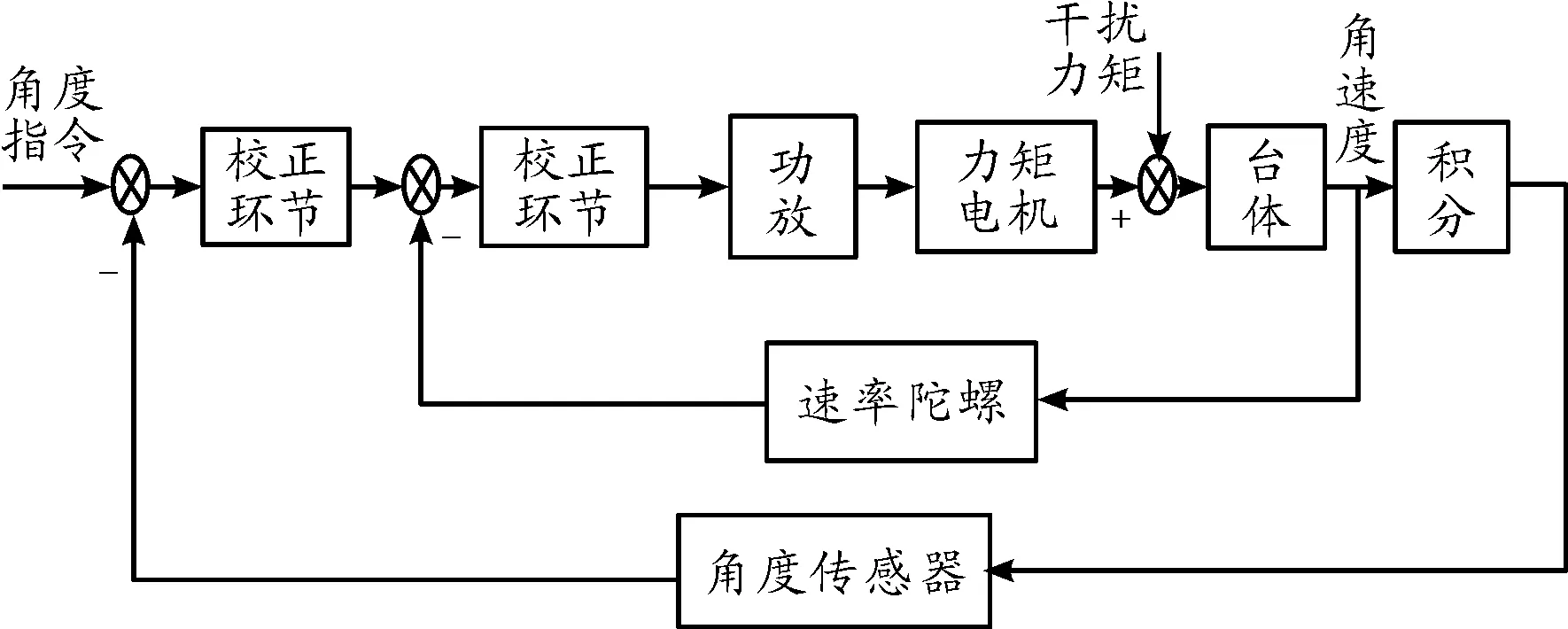
图1 导引头控制系统原理框图

滚仰式半捷联导引头稳定平台的主要功能是保持导引头光轴稳定，隔离弹体扰动，对目标实现精确跟踪。当弹体姿态剧烈变化或导引头受到外界扰动时，图像系统输出的失调角有可能会出现跳动现象，进而影响导引头跟踪的稳定性。为避免这种影响，导引头控制系统应该具有较高的跟踪精度和稳定精度、具有对目标的快速跟踪能力，其控制器的设计和控制策略的选择是实现导引头功能的关键所在。同时为实现对目标的精确制导，要求导引头必须具备良好的控制性能以确保交会过程中对目标快速稳定跟踪。

3 基于卡尔曼滤波的导引头控制

3.1 卡尔曼滤波原理

卡尔曼滤波算法中利用到了系统状态方程、量测方程、测量误差的统计特性和白噪声激励的统计特性等，卡尔曼滤波本质是递推无偏线性最小方差估计，估计结果在线性估计中精度最佳[10]，下面简单介绍下卡尔曼滤波原理。

设系统的状态方程为

Xk=Φk,k-1Xk-1+Γk,k-1Wk-1

(1)

设系统的量测方程为

Zk=HkXk+Vk

(2)

其中:Xk为状态向量，Xk-1为上一时刻的状态向量，Φk,k-1为状态转移矩阵，Γk,k-1为过程噪声输入矩阵，Wk-1为过程噪声序列，Zk为量测值，Hk为量测矩阵，Vk为测量噪声序列。

若满足式(1)和式(2)的线性随机系统的过程噪声和量测噪声为高斯白噪声且它们不相关，则可得到下述卡尔曼滤波方程。

比较两组的手术时间、术中出血量和手术费用。采用日本骨科协会评分（JOA评分）评估患者神经功能，改善率计算方式如下：神经功能改善率=（治疗后JOA评分-治疗前JOA评分）/（17-治疗前评分）×100%。

1) 状态一步预测方程：

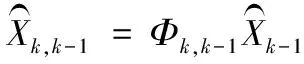
(3)

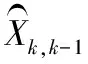
2) 一步预测均方误差：

(4)

其中:Pk,k-1为状态预测的均方误差矩阵，Qk-1为过程噪声方差。

3) 滤波增益：

(5)

其中Rk为量测噪声方差阵。

4) 状态估计方程:

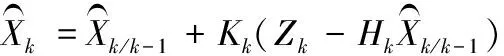
(6)

Pk=(I-KkHk)Pk/k-1

(7)

式(3)～式(7)即为离散形式的卡尔曼滤波基本方程，该滤波方法能够在线性高斯模型条件下，对目标状态做出最优估计[10]。

3.2 导引头状态方程与量测模型

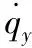
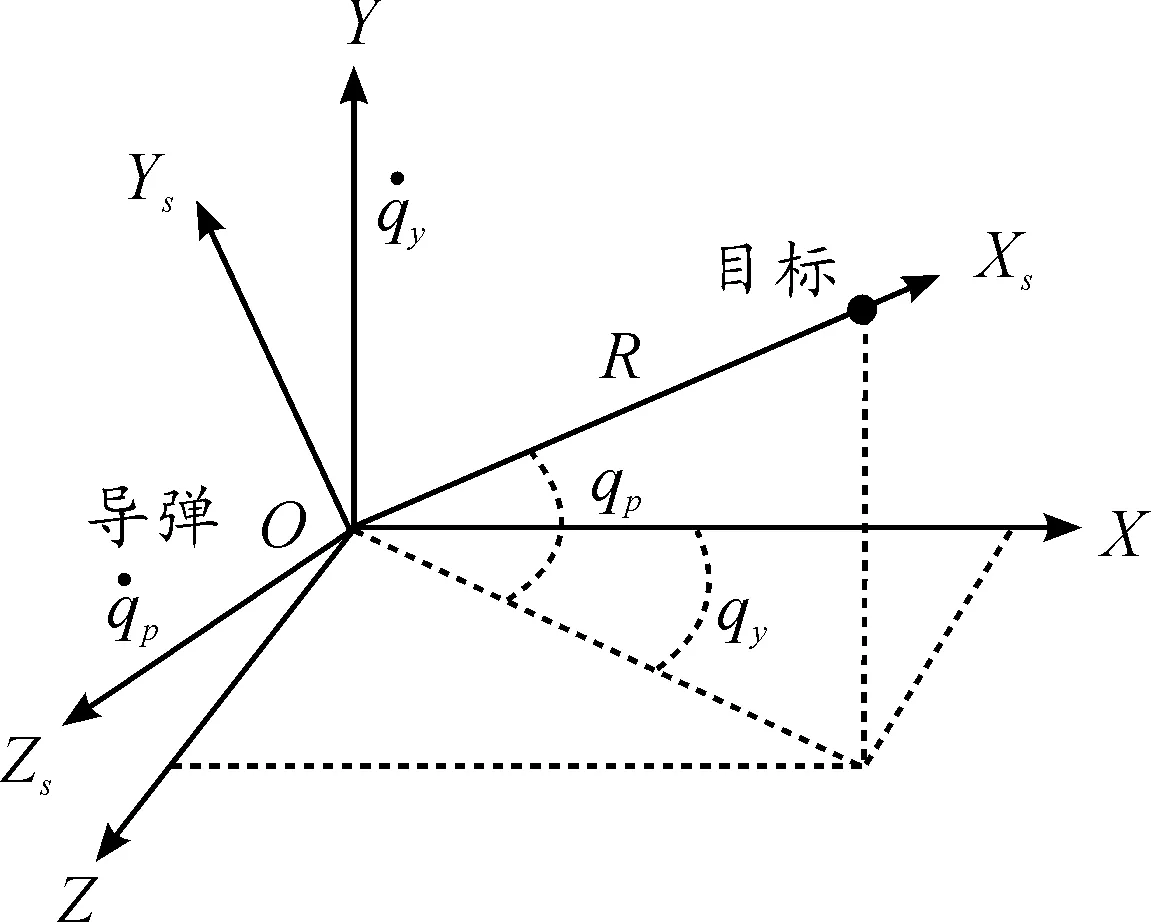
图2 惯性坐标系和视线坐标系的关系

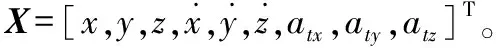
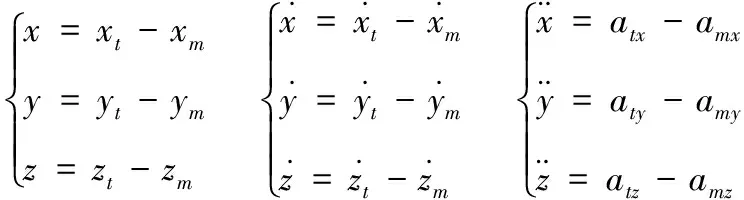
(8)

假设目标为常加速度运动模型，把目标的加加速度作为随机白噪声处理，可得：

(9)

wx、wy、wz为高斯白噪声，则导引头的状态方程可表示为

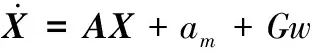
(10)

由于导弹自身加速度可量测，式(10)中导弹加速度am为已知输入量。因此在惯性坐标系下导引头的状态方程是线性的，其中：

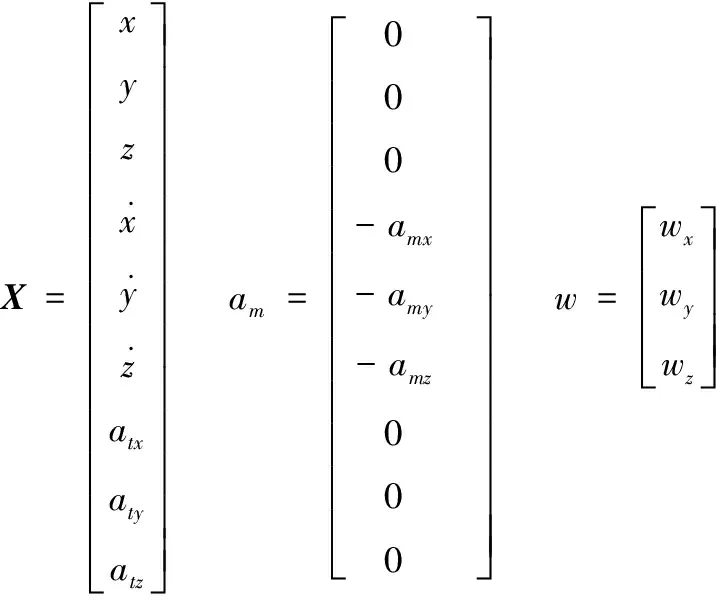
由图2惯性坐标系与视线坐标系的位置关系可得：

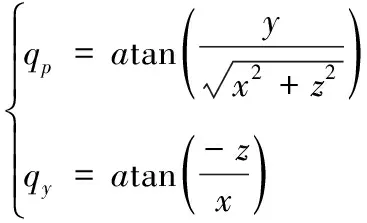
(11)

根据导引头框架角、图像失调角等可以得到弹目视线角，因此导引头量测方程为

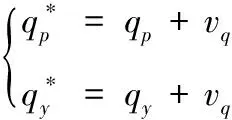
(12)

根据导引头状态方程和量测方程，可采用卡尔曼滤波器进行目标运动状态估计，实现对半捷联导引头的稳定控制与快速跟踪。

4 仿真分析

根据滚仰式半捷联导引头稳定与跟踪原理，采用基于目标运动状态估计的卡尔曼滤波方法对导引头进行控制，导引头控制仿真模型如图3所示。其中PID控制器的参数设置为kp=10、ki=1、kd=1，取采样时间为1 ms。设导引头控制干扰信号其均值为0度，方差为0.02。设导引头探测器测量值的偏差其均值为0度，方差为0.02。

为了评估半捷联导引头采用卡尔曼滤波方法对运动目标的跟踪效果，给系统输入正弦激励信号u=sin(2πt)。理想信号及带有噪声的信号如图4所示、理想信号及滤波后的信号如图5所示。从图5中可以看到，卡尔曼滤波方法对控制干扰和测量噪声具有良好的滤波作用，导引头控制系统的响应结果很好的复现了期望的轨迹，控制误差接近于0。

图3 滚仰式半捷联导引头控制仿真模型示意图

图4 理想信号及带有噪声的信号

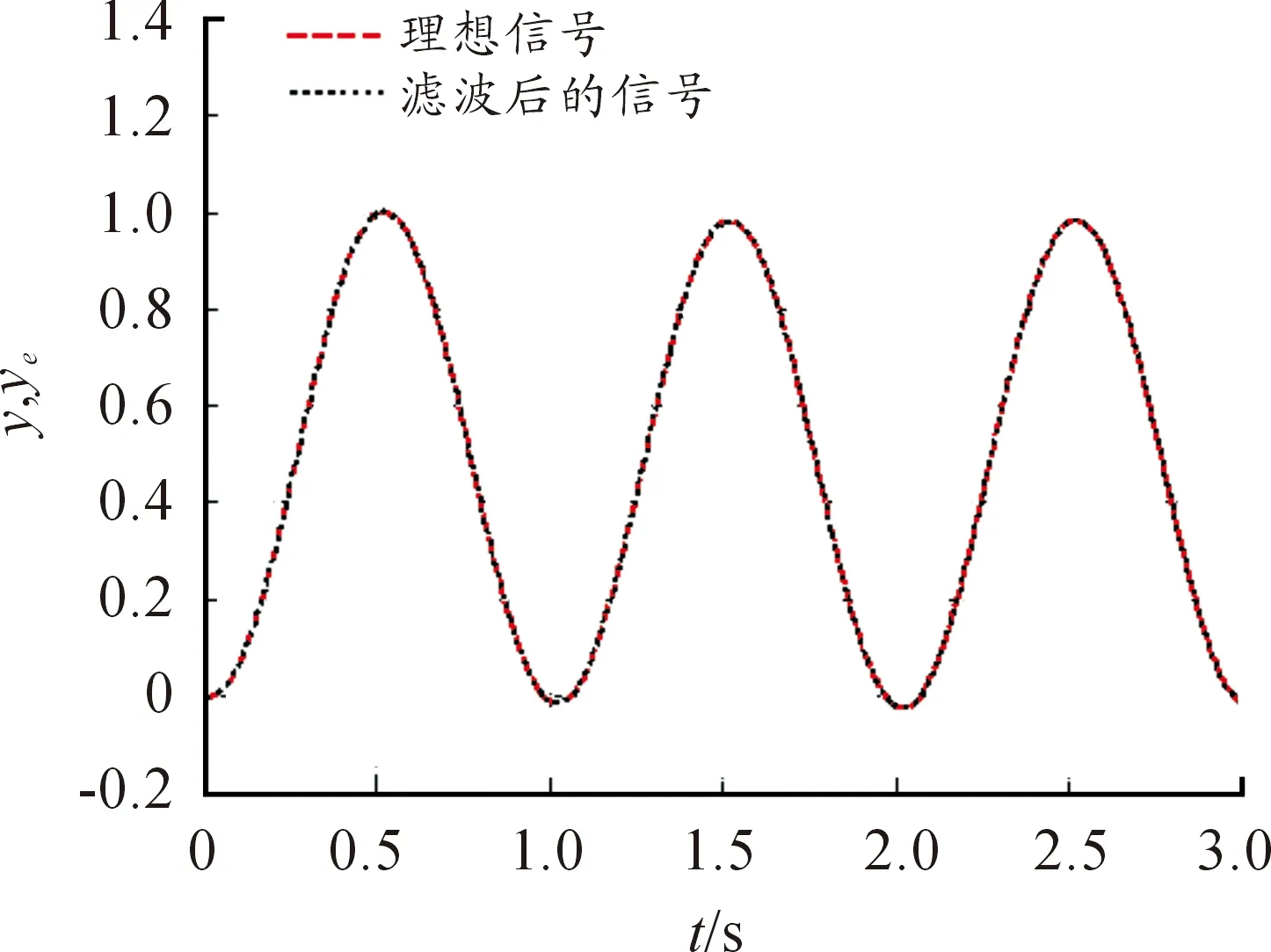
图5 理想信号及滤波后的信号

从以上仿真结果可以看出：基于目标运动状态估计的卡尔曼滤波方法应用于半捷联导引头控制系统，对控制干扰和测量噪声具有良好的滤波作用，能够有效提高导引头控制系统的鲁棒性。

为了进一步验证该控制算法的性能，在半捷联导引头稳定与跟踪一体化仿真模型中，假设目标的运动方程为x(t)=8 000，y(t)=2 000+300*sin(0.5t)，z(t)=2 000+300*cos(0.5t)。设导引头控制干扰信号其均值为0度，方差为0.02。设导引头探测器测量值的偏差其均值为0度，方差为0.02的白噪声。考察在噪声作用下滚仰式半捷联导引头对运动目标的跟踪性能。由图6、图7可知：在干扰信号和测量噪声作用下滚仰式半捷联导引头可始终保持对目标的稳定跟踪，跟踪误差可控制在2个像素以内。运动目标在滚仰式半捷联导引头瞬时视场内的轨迹如图8所示，可以看出目标始终在导引头瞬时视场内。基于目标运动状态估计的卡尔曼滤波方法能够使滚仰式半捷联导引头在扰动和噪声作用下保持对运动目标持续稳定的跟踪。

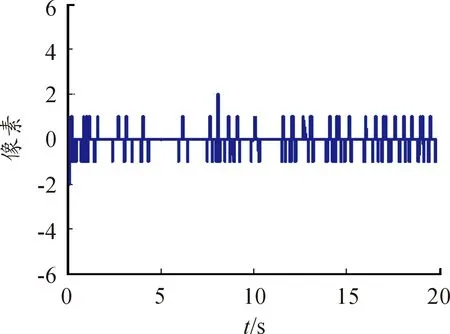
图6 X向导引头跟踪误差

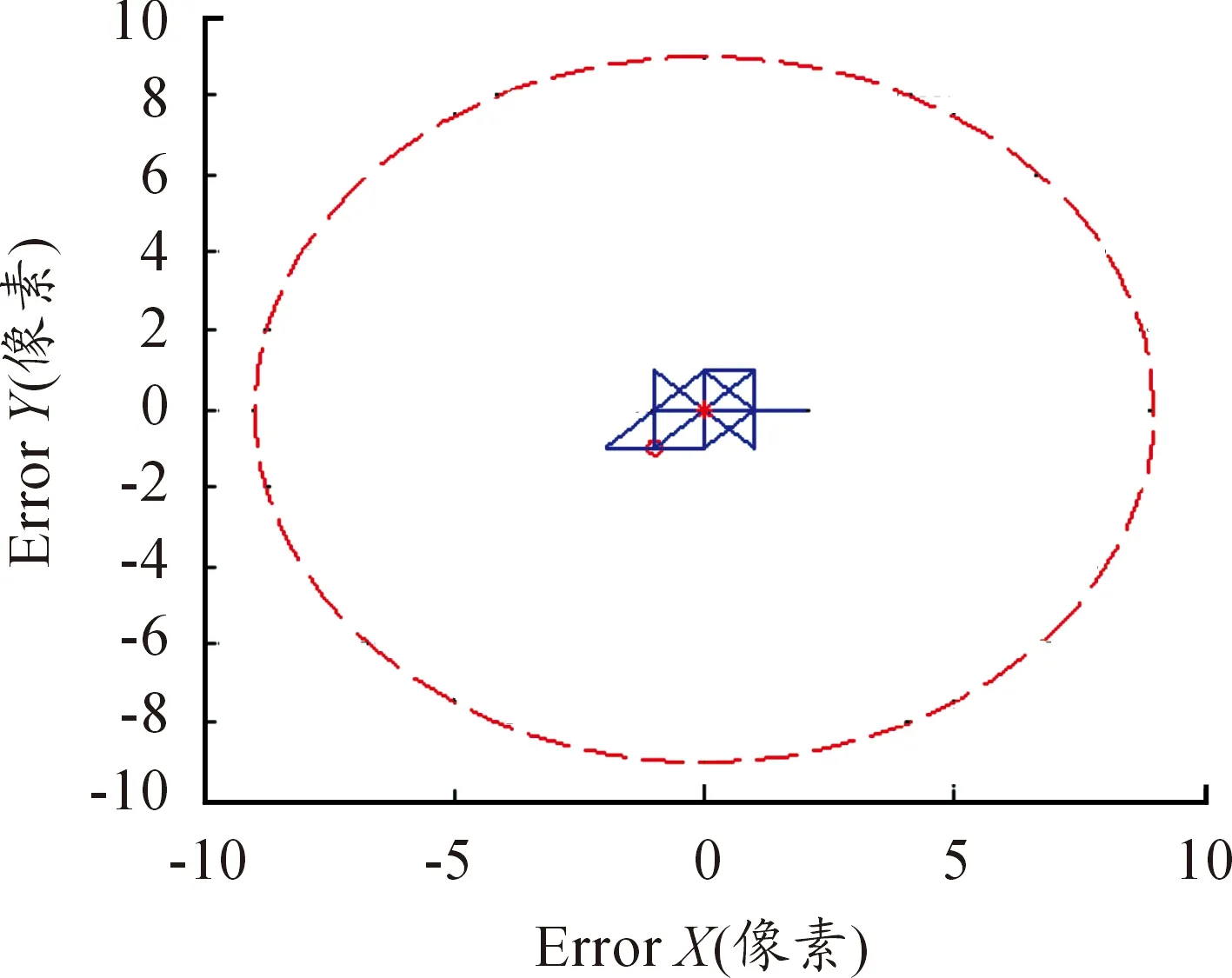
图8 导引头瞬时视场中目标运动轨迹

5 结论

本文提出的基于目标运动状态估计的卡尔曼滤波方法应用于半捷联导引头控制，使导引头对控制干扰和测量噪声具有良好的滤波作用，能够有效提高导引头控制系统的鲁棒性。仿真结果表明，采用基于目标运动状态估计的卡尔曼滤波方法应用于导引头控制，能够使导引头控制回路的自适应能力得到提高，能够使导引头在干扰和噪声作用下实现对运动目标的稳定跟踪，为滚仰式半捷联导引头的控制系统设计提供参考。