基于概率累积的非通视无源定位方法

王 伟, 王钦钊, 沈 岚, 王 波,*, 丁 怀

(1. 中国人民解放军陆军装甲兵学院兵器与控制系, 北京 100072;2. 北京特种车辆研究所, 北京 100072; 3. 电子信息控制重点实验室, 四川 成都 610036)

0 引 言

在复杂城市环境下,目标辐射源与接收机之间存在大量建筑物等客体对象,辐射信号经过多次反射、散射被定位系统接收,非通视(not line of sight, NLOS)传输引起的辐射源无源定位偏差问题一直以来都受到研究者的广泛关注。NLOS误差是指在接收机与辐射源之间的直线传播路线中由于存在建筑物、高墙等障碍物的影响导致的电磁传播路径改变而引起的与直线传播路线之间的测量误差。分布式无源定位技术采用分散配置的多个传感器接收目标信号[1],但由于NLOS误差在复杂城市环境中普遍存在,辐射源位置估计精度仍具有很大的进步空间。找到一种可以控制误差并提升定位精度的合适方法,对提高无源定位技术在城市环境中应用的有效性和可靠性具有重要意义。

目前国内外学者的大量研究将主要关注点放在了如何消除基于到达时差(time difference of arrival, TDOA)的定位中的NLOS误差上,通过在NLOS与通视(line of sight, LOS)测量路径上布置大量接收机作为测量点,基于NLOS误差模型,尝试通过某些已知信息,对测量结果进行数学上合理的近似处理[2-10],以减小或直接忽略NLOS测量对结果的影响。例如,通过计算一系列距离测量值的标准差,并与某一门限值作对比,识别出其中的NLOS距离测量值,随后使用带有额外未知常数的卡尔曼滤波器去重构NLOS距离偏差估计位置参数[11-18];在文献[19]中,作者首先评估了哪些接收机到辐射源之间的传播是NLOS路径,随后直接将这些NLOS路径剔除,随后再将剩余的接收机采集值进行三角测量法定位;Wylie[20]等人通过观察发现,NLOS测量的距离方差要远远大于LOS测量的距离方差,他提出一种假设性测试,基于距离测量的连续排列以识别NLOS测量,如果知道距离测量的误差模型,则可以生成更有效的NLOS测量识别假设性测试;将NLOS和LOS测量作为高斯随机变量,Borras等人[21]分别推导出了参数化和非参数化的假设测试的理论框架,但是关于NLOS偏差的随机分布类型的假设有很多,如高斯分布[22]、均一分布、指数分布[5,19,22-23]、瑞利分布、莱斯分布、卡方分布[24]等;Kobayashi假定在目标位置NLOS误差满足类似于上述提到过的某些概率分布类型,推导出指定概率统计模型时的测量下界问题。此外,文献[25-29]的研究人员关注了如何在移动条件下对辐射源进行定位。Boccadoro等人[25]提出关联概率分布与粒子滤波结合的算法,通过概率分布最大化寻找辐射源可能的位置,然后利用粒子滤波将不可能的估计位置点除去,形成辐射源的运动轨迹;Jeong等人[26]同样采用了粒子滤波法处理运动目标的定位问题;Dogancay[27]提出一种具有高效计算能力的递归最小二乘算法,它能对连续变化的静态位置进行评估以获得最大似然估计值;文献[28-29]中,研究人员使用互作用的多重卡尔曼滤波模型(interacting multiple models Kalman filters, IMMKFs)去跟踪基于TDOA测量的辐射源目标。

从上述的介绍可以看出,关于NLOS条件下的无源定位有大量的修正方法,基于TDOA的修正方法大多是利用NLOS误差的特征在辐射源的位置评估时进行误差消除。但是在不同城市环境下,这种NLOS误差特征各不相同,因此适用性也不理想。

在本文中,提出了一种基于概率累积的辐射源定位方法。通过随机分布多个接收机,任意组合成多个不同的三点测量系统,将每个三点测量系统测出的辐射源位置的分布概率进行分布累加,累积概率的极大值处即对应辐射源位置。针对一种较为特殊的场景,使用该方法对不同位置处的辐射源进行了仿真验证,在接收机定位误差分别为3 m和15 m时得到的辐射源位置偏差相差不大,在接收机定位误差为15 m条件下大多数辐射源定位误差均小于30 m,平均测量偏差为19.4 m。进一步地,在结论中分析了该方法后续有待优化解决的问题。

1 无源定位模型

1.1 无误差模型

根据3个接收机的位置与测量时间差,可列出方程为

(1)

整理可得:

(2)

因此,辐射源的位置为

(3)

式中:M-1是M的逆矩阵。对于任何无测量误差的系统,可以通过式(3)计算出辐射源的位置。

1.2 NLOS无源定位模型

对于NLOS环境下的无源定位,由于存在测量误差,则式(1)可写成:

(4)

(5)

式中：σx与σy为x和y方向上的测量标准差;ρ为两个方向的相关系数。对于一次测量,计算出的分布大概率是偏离真实位置的。多个不同的系统测量出的分布累加为

(6)

因为每个三点测量系统测出的位置都是在真实位置附近分布的,因此多个测量的分布累加的累积概率分布应在辐射源真实位置处存在最高值,如图2所示。

对于式(5),关键在于求出σx、σy和ρ。这3个参数是与测量误差以及辐射源的位置有关的物理量。对于式(4),可以对时差测量值进行分析,假设时差测量存在变化,则

(7)

由此可得x和y的偏差为

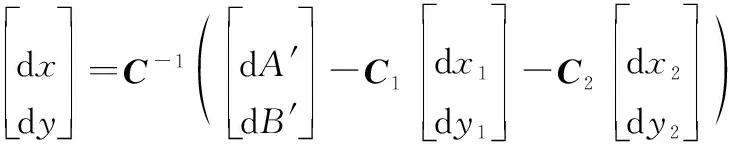
(8)

由于不同变量之间是无关的,因此交叉项均为0,则dr的协方差矩阵为

(9)

上述协方差矩阵的形式为

(10)

对于式(9)中右边的几个协方差矩阵,接收机位置误差的协方差为

(11)

式中：σi是第i个接收机位置的标准差,当使用GPS定位时,定位误差σi=3～15 m。测量误差的协方差为

(12)

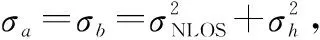
2 模型仿真

针对一种较为特殊的场景,利用计算机仿真验证上述方法的有效性以及不同参数对定位结果的影响。

场景1首先在1 km×1 km的区域内产生数个尺寸随机的正方形二维建筑,并随机设置辐射源及接收机的位置。为了验证对NLOS问题的解决能力,我们设置的所有接收机与辐射源之间均为NLOS条件,如图3所示。图中的线段表示电磁波由辐射源到接收机的最短传播路径,其中一共随机布设20个接收机,辐射源位置为r0(500,530),接收机的定位误差分别设置为σgps=3 m和σgps=15 m。从图中可以看出,NLOS引起的路径偏差非常显著。

对于场景1中的建筑分布,其NLOS偏差δ与Δ分别如图4所示,标准差σ=145.89 m。

利用模型提出的算法,计算出σgps=3 m和σgps=15 m两种定位误差下的位置测量结果的累积概率分布如图5和图6所示,在计算累积分布时,将空间划分为500×500的网格,每个网格的尺寸为2 m×2 m,因此位置分辨率为1 m。由图中看出两种定位误差下,分别在位置r′(491,543)处和r′(511,539)处存在极大值,按照上述方法,该处存在辐射源的概率最大,因此辐射源的评估位置为r′,与真实辐射源的位置偏差分别为ΔL=15.81 m和ΔL=14.21 m。从计算结果可以看出,由于NLOS的误差σ=145.89 m相较于定位误差大很多,因此定位误差的结果对最终结果的影响较小。在本文中的计算均以定位误差σgps=15 m进行计算。

为了考察该方法下采样点数量对结果的影响,分别研究了不同采样点数时的位置测量相对于真实位置的偏差,如图7所示。在图7中,辐射源仍放置于r0(500,530)位置处。不同的曲线代表的是在固定辐射源位置的前提下的不同接收机的位置分布形式。从图中可以看出,当接收机数量N=5时,位置测量误差与分布形式有显著的关系。有些情况下误差较小,另一些情况时计算结果明显发散,这说明5个接收机的数量不满足定位需求。随着接收机数量的增加,位置测量误差迅速减小,在某些分布形式中甚至达到了几米的误差精度,这可能是由于在该种分布形式下,辐射源到接收机的路程偏差较小或互相之间刚好形成了抵消,使得定位结果很精确。然而这种情况在实际测量中并无法知道是何种分布,因此不具有普遍适用性。继续增加接收机的数量,各种不同的位置分布的接收机最终形成的测量误差收敛于一个稳定值,这个接收机数量的临界值在该系统中约为20。

为了验证方法在不同位置上均具有可行性,我们在图3场景中半径为450 m的圆域内随机抽取500个位置点,使用20个接收机进行定位,其辐射源定位结果相对于真实辐射源位置的偏差如图8所示。图8(a)为抽取其中部分位置处的定位偏差图。蓝色正方形区域对应图3中的建筑物位置,红色细圆柱体的位置表示辐射源位置,高度表示辐射源在该处时定位值相对于真实值的偏差,柱体越高代表偏差越大。透明墨绿色大柱体的半径代表圆域的大小,而高度对应着红色柱体偏差为30 m的位置,可以看出偏差的整体大小。图8(b)为利用每个采样点位置处的值利用双线性插值得到的平面上所有位置处的偏差分布。可以看出几乎所有位置处的辐射源定位误差均小于30 m,而有些位置处的偏差只有几米。对这一区域内位置偏差进行统计,最终的平均测量偏差ΔL为19.4 m,这一误差精度可满足城市中辐射源定位的精度要求。

3 结 论

在本文中,针对存在大量建筑遮挡的NLOS环境,提出了一种基于测量误差累积概率分布的辐射源定位方法。将该方法应用于具体的应用场景中,当不存在通视测量且非通视测量偏差极大的情况下,该方法在场景的大多数位置处均有较好的定位结果,与接收机本身的定位误差无显著相关性,且定位误差结果随分布式传感器数量的增加呈迅速收敛状态。结果表明上述定位方法在拥挤或复杂环境下具有一定的可行性,且误差满足指定大小区域时的一般误差要求。然而,本文的方法还存在一些有待解决的问题。首先,用于定位的接收机数量较多,且当环境的随机性变得更大时,需要更多的接收机才能达到所需的收敛效果;其次,该方法在不同位置处的测量误差的变化区间较大,这与所处位置附近处的建筑分布情况有一定的关系;最后,接收机的不同布局也会导致测量误差的不同,在接收机数量较少时这种现象更为显著。从上述3个问题可以看出,本文提出的方法虽然避免了具体城市环境非通视测量误差分布对计算模型及结果的影响,但在辐射源位置估计精度满足要求的情况下,方法的定位收敛速度与环境具体布局有关,在后续的研究中,需要针对接收机的布局位置策略等进行优化,以提升方法在NLOS环境下的定位能力。