基于改进型离散滑模观测器的表贴式永磁同步电机无位置传感器控制

佟诚德，葛 晨，郭家旭，郎杰文，王明峤，郑 萍

（哈尔滨工业大学电气工程及自动化学院，哈尔滨 150080）

0 引言

永磁同步电机的无位置传感器技术按照工况与原理大致可以分为两类：基于电机基频模型检测位置与基于转子凸极性检测位置[1-3]。基于电机基频模型检测位置的方法适用于中高速情况，一般为电机额定转速10%以上[4]。电机在运行过程中，三相绕组会产生相位相差120°的反电势，根据电机模型，通过判断反电势的相位，即可确定转子位置。通常，基于模型法观测转子位置／速度可以分成三部分：反电势／磁链观测器、位置估计误差解调以及位置／转速跟踪器[5]。其中，观测反电势或磁链通常采用的方法有：磁链估计法[6-7]、模型参考自适应法[8-9]、扩展Kalman滤波器法[10]以及滑模观测器法[11-12]等。位置误差解调可以通过估算反电势或者磁链进行简单的算术运得到，转子位置／转速跟踪可以通过使用锁相环或Luenberger观测器实现。

滑模观测器由于其结构简单、设计方便、具有较强的鲁棒性，国内外学者对其进行了大量研究。通常情况下，滑模观测器是在连续域进行设计，再将其离散化，应用到实际的电机控制系统当中。通过该方法得到的离散滑模观测器的稳定性与直接采用离散滑模控制理论得到的稳定性会有所差异，最终会影响到观测器的性能。同时，传统的滑模观测器通常采用低通滤波器来获得反电势的估计值，为了解决低通滤波器带来的相移，需要对最终结果进行补偿。为了解决以上问题，本文在离散滑模控制理论的基础上，提出了一种基于自适应反电势滤波器的改进型离散滑模观测器。该观测器由三部分结构组成：基于趋近律设计的离散滑模观测器、离散自适应反电势滤波器以及带稳态误差补偿的归一化锁相环。将基于趋近律设计的滑模观测器输出通过自适应反电势滤波器滤波，得到反电势的估计值，再将其输入到归一化锁相环，并对电机加减速过程中的稳态误差进行补偿，即可得到最终的位置信息，从而完成无位置传感器控制。通过仿真，对所提出的改进型离散滑模观测器进行了验证。

1 传统滑模观测器抖振分析

1.1 电机模型

对于表贴式永磁同步电机，其α-β轴系下的数学模型为

式（1）中，vα、 vβ为定子相电压 α 轴、 β轴对应分量，iα、iβ为定子电流α轴、β轴对应分量，Rs为定子电阻，Ls为定子电感，ψf为永磁磁链，ωe为电机的电角速度，θe为d轴与定子A相轴线的夹角。

采用零阶保持器得到电机在α-β轴系下的离散化模型

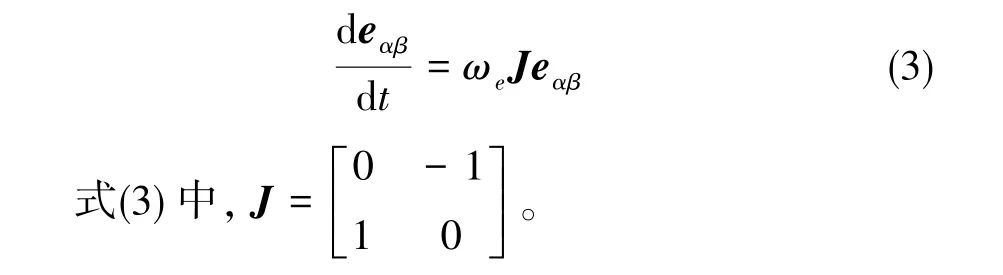
采用后向Euler法将式（3）进行离散化，根据假设可以得到 ωe（k+1）≈ ωe（k）， 结果如下

1.2 传统滑模观测器抖振分析

选择定子电流误差为滑模面，有

传统离散滑模观测器的结果为

根据电流误差方程，通过稳定性分析可以得到滑模增益的取值范围，滑模增益应始终大于当前转速下电机的反电势

为减小抖振，采用与转速相关的自适应滑模增益

由于 A 的值接近于 1， 因此（A-1）s（k）项相对于反电势项 eαβ（k）可以忽略不计。 因此， 当 s（k）＞0 时， 相邻两次跟踪误差差值 Δs（k）≈ eαβ（k）-k1a。当 s（k）＜0时， 相邻两次跟踪误差差值Δs（k）≈eαβ（k）+k1a。 在对观测器进行设计时， 为了减小抖振，通常使滑模增益k1a略大于反电势的最大值。由式（9）可知，当跟踪误差位于滑模面两侧时， Δs（k）不同。 当反电势 eαβ（k）接近于 0 时，。 此时，在相邻的控制周期中，跟踪误差可以反复穿越滑模面。当eαβ（k）接近峰值时，Δs（k）最大可以接近反电势幅值的两倍，最小则接近于0，此时往往需要数个控制周期，跟踪误差才可以穿越滑模面，这使得抖振现象更加严重，其现象示意图如图1所示。

图1 跟踪误差位于滑模面两侧时的示意图Fig.1 Schematic diagram of tracking errors on both sides of the sliding mode surface

2 改进型离散滑模观测器设计

2.1 基于趋近律设计的离散滑模观测器

为了减小传统离散滑模观测器的抖振，采用基于趋近律设计的离散滑模观测器。该观测器不仅可以很好地改善趋近运动的动态品质，同时由于引入了反电势项，从根本上解决了传统离散化观测器由于在滑模面两侧趋近速度不同所带来的抖振，从而使系统抖振大大减小。

采用后向Euler法将由指数趋近律与等速趋近律组成的组合趋近律进行离散化，其形式为

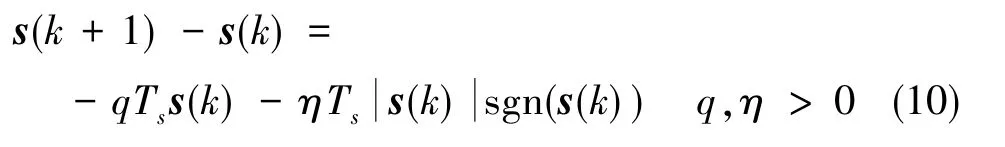
设计的离散滑模观测器满足

由式（11）可以得到电流误差方程

定义滑模面

由式（10）、 式（12）与式（13）可得

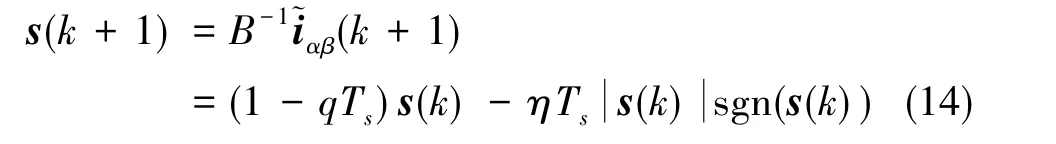
由式（14）可以得到反电势的等效控制项

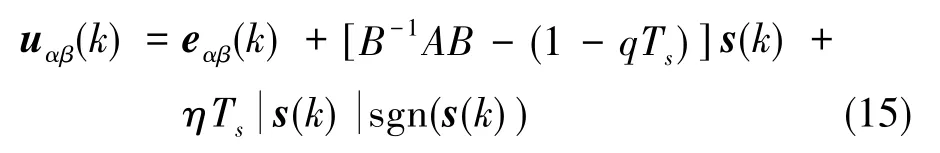
采用离散滑模观测器时，在相邻两次控制中跟踪误差差值Δs（k）的表达式如式（10）所示。 基于趋近律设计的滑模观测器规定了系统运动点趋近于滑模面的运动规律，因此不会出现趋近速度不同的问题。将其与传统离散滑模观测器进行对比，虽然传统滑模观测器选择符号函数作为切换函数，但是真正作用到系统上的实际控制项如式（9）所示，从而使观测结果产生严重的抖振。而基于趋近律设计的滑模观测器虽然等效控制项较为复杂，如式（15）所示，但是其实际控制项为式（10），由于不存在 eαβ（k）项，因此不会出现趋近速度不同的情况。

根据离散滑模的可达性条件，可以得到基于趋近律设计的滑模观测器参数取值范围

2.2 离散自适应反电势滤波器

通常情况下，将由滑模观测器得到的等效控制项eαβ（k）通过一阶低通滤波器，滤除信号中的高频分量，即可得到反电势的估计值，进而得到位置信息的估计值。但是，低通滤波器存在相位延迟与幅值衰减，为了对得到的位置信息进行补偿，补偿值通常由估计的位置信息进行计算，由于估计的位置信息存在误差，将会导致补偿值计算不准确，从而使最终结果产生一定误差。为了避免低通滤波器所带来的相位延迟与幅值衰减，提出一种离散自适应反电势滤波器来代替低通滤波器，由反电势滤波器的结果得到位置信息的估计值。

将由自适应反电势滤波器得到的反电势估计值反馈回前述设计的滑模观测器中，即可得到完整的基于趋近律设计的离散滑模观测器，其结构如图2所示。可以看出，自适应反电势滤波器代替了传统滑模观测器中低通滤波器的位置。

图2 基于趋近律设计的离散滑模观测器结构图Fig.2 Block diagram of discrete sliding mode observer based on approach law

2.3 归一化锁相环及其稳态误差补偿

采用锁相环来对位置信息进行解算，由于传统锁相环的频响特性会随着输入反电势幅值变化而改变，对于固定的锁相环参数，其带宽是一个变化的范围，不利于锁相环的参数设计。因此对锁相环输入进行标幺化处理，得到归一化的正交锁相环，其结构框图如图3所示。

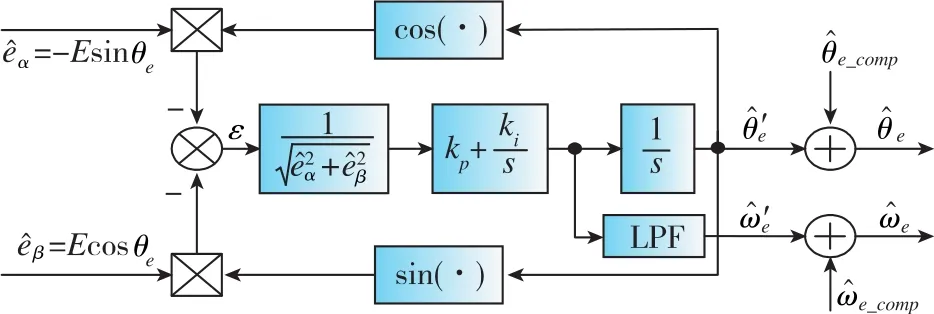
图3 归一化锁相环结构示意图Fig.3 Schematic diagram of normalized phase-locked loop

锁相环直接输出的位置信息在电机加减速过程中存在稳态误差，假设电机的电角速度与电角加速度满足

式（24）中，a为电机的电角加速度，单位为rad ／s2。

可以看出，当电机处于加减速过程中时，由于a≠0，θe相当于单位加速度输入，因此锁相环对于角度估计值输出存在稳态误差，根据终值定理可得此时的稳态误差

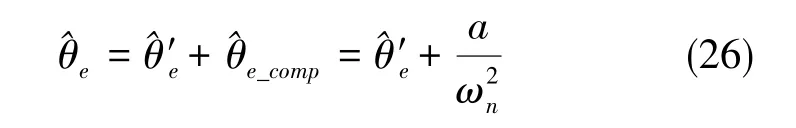
由于锁相环直接输出的转速估计值通常含有较大的抖振，因此一般将其通过低通滤波器，可得到较为平稳的结果。低通滤波器对单位斜坡输入存在稳态误差，对于转速估计值，其稳态误差值为

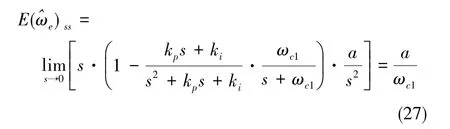
将式（27）作为转速补偿值，即可以得到转速估计值的最终结果

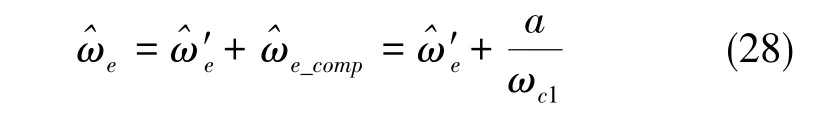
角度补偿值与转速补偿值均需要电机的角加速度来进行计算，在无位置传感器控制系统中，可以采用观测器得到的估计转速通过数学运算来计算加速度，该方式会不可避免地影响电机稳态时位置信息的估计精度。

将锁相环进行离散化，可以得到离散锁相环。如图4所示，将前述基于趋近律设计的离散滑模观测器、反电势滤波器与锁相环依次连接，即可得到改进型的离散滑模观测器。

图4 改进型滑模观测器结构图Fig.4 Block diagram of improved sliding mode observer

3 仿真验证

在Matlab／Simulink中搭建相应的仿真模型进行仿真，电机参数如表1所示。首先对比分析采用补偿策略与未采用补偿策略时归一化锁相环的性能。电机先加速后减速，电机加减速过程中估算转速与实际转速的对比结果如图5所示。可以看出，估算转速可以较好地跟踪实际转速。

表1 电机参数Table 1 Parameters of motor

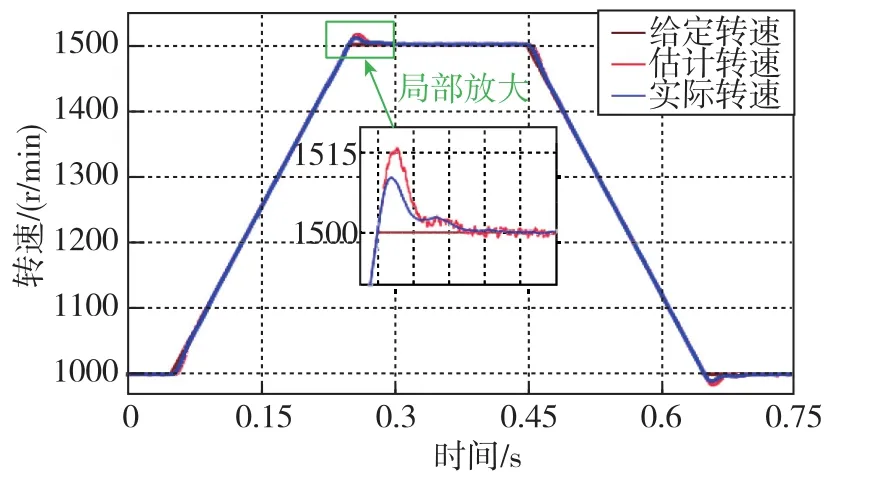
图5 电机加减速过程中估计转速与实际转速对比结果Fig.5 Comparison between estimated speed and actual speed during motor acceleration and deceleration

采用与未采用补偿时的锁相环输出对比结果如图6所示。对锁相环输出进行补偿之后，除了在电机加减速瞬间角度与速度估计误差有一个小的跳变，在其余加减速过程中的估计误差与稳态时差别不大，角度估计误差为±0.4°，转速估计误差为±1.5r／min。对于未进行补偿的情况，在稳态时，角度估计误差为±0.2°，转速估计误差为±0.5r／min。当电机加速时，角度估计误差扩大至约3.6°，转速估计误差扩大至约16r／min。由结果可以看出，由于补偿值需要对估计转速进行微分得到，因此补偿过后稳态时的角度与速度估计误差相对于未补偿时具有更大的波动，不过不会出现过大的估计误差。

图6 电机加减速过程中角度与转速估计误差对比Fig.6 Comparison of angle and speed estimation errors during motor acceleration and deceleration

对自适应反电势滤波器进行仿真分析。电机参考给定在0.3s时进行加速，在0.75s时加速至额定转速3200r／min，之后保持额定转速至1.0s。仿真时，位置解算模块采用带补偿的锁相环。分别采用自适应反电势滤波器与低通滤波器，得到的α轴反电势观测结果如图7所示。可以看出，采用低通滤波器时，估计反电势在相位上滞后于实际反电势；采用反电势观测器时，其估计反电势于实际反电势十分接近，反电势误差在±2V之内。分别采用自适应反电势滤波器与低通滤波器，得到的反电势估计值进行位置解算后的位置估计误差对比结果如图8所示。对于采用低通滤波器的方式，电机转速为1000r／min时，角度估算误差约为3°。随着电机转速增加，反电势频率也在增加，导致相位延迟逐渐严重，角度估算误差也随之增加，在3200r／min时约为9.5°。对于采用自适应反电势滤波器的方式，在整个过程中，角度估算误差都在1°以内。虽然采用低通滤波器时角度估计值存在相位延迟，但是由于两种策略得到的反电势频率均与实际反电势相同，因此两种策略得到的转速估算误差均在0附近波动。

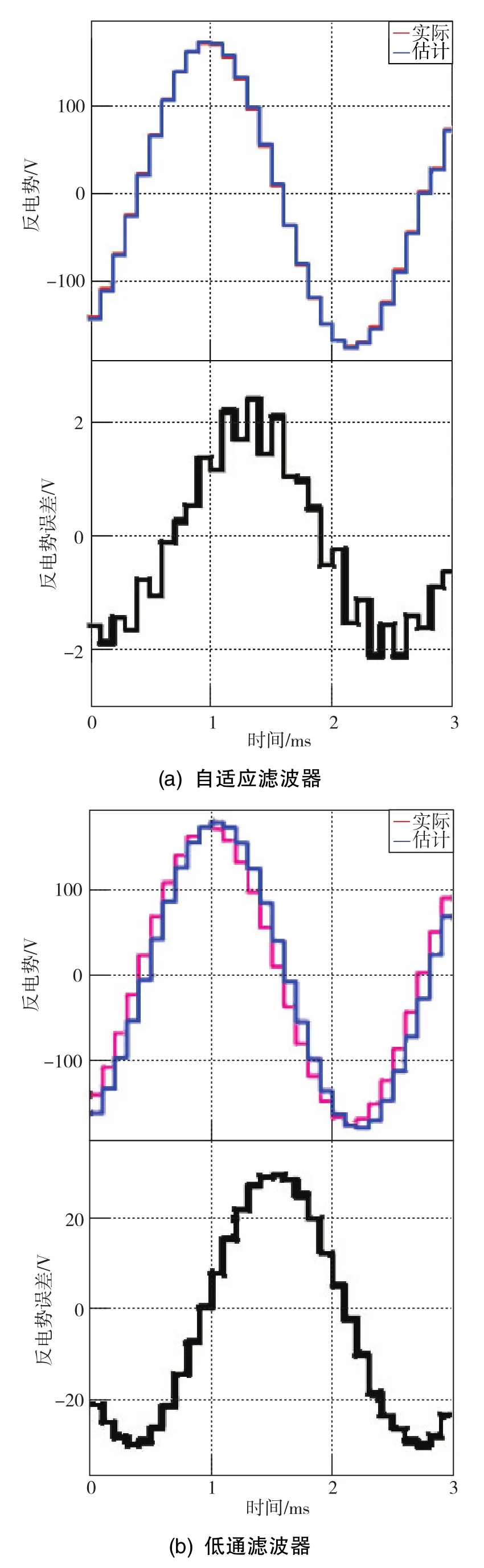
图7 α轴估算反电势对比Fig.7 Comparison ofα-axis estimated back-EMF

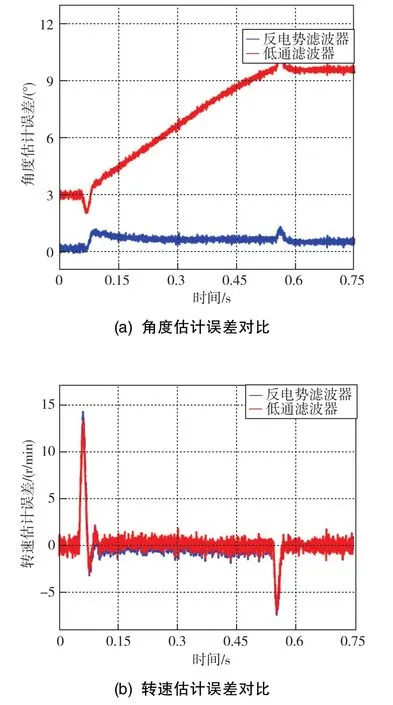
图8 两种滤波器的估计误差对比Fig.8 Comparison of estimation errors between two kinds of filters

最后，针对传统滑模观测器与基于趋近律设计的改进型滑模观测器进行仿真对比分析，电机转速从0r／min逐渐加速至额定转速3200r／min，然后保持该转速运行。分别采用基于趋近律设计的滑模观测器与传统滑模观测器，得到的定子电流α轴分量如图9所示。

由图9（b）可知，采用传统滑模观测器时，在滑模面两侧趋近速度不同，当定子电流误差位于图中A点处时，相邻两次观测误差 Δs（k）接近于0，导致需要数个控制周期才可以使定子电流误差穿越滑模面；而在图中B点处，相邻两次观测误差 Δs（k）接近于两倍的 eαβ（k）， 因此只需要一个控制周期就可以使定子电流误差穿越滑模面。由于在滑模面两侧趋近速度不同，导致观测电流与实际电流误差较大，从而产生严重的抖振现象。而采用基于趋近律设计的滑模观测器时，不存在在滑模面两侧趋近速度不同的现象，观测电流与实际电流误差在±5V之内，远远小于传统滑模观测器的观测误差。但是由于离散滑模不能产生理想的滑动模态，只能产生准滑动模态，因此电流跟踪误差无法减小到零。

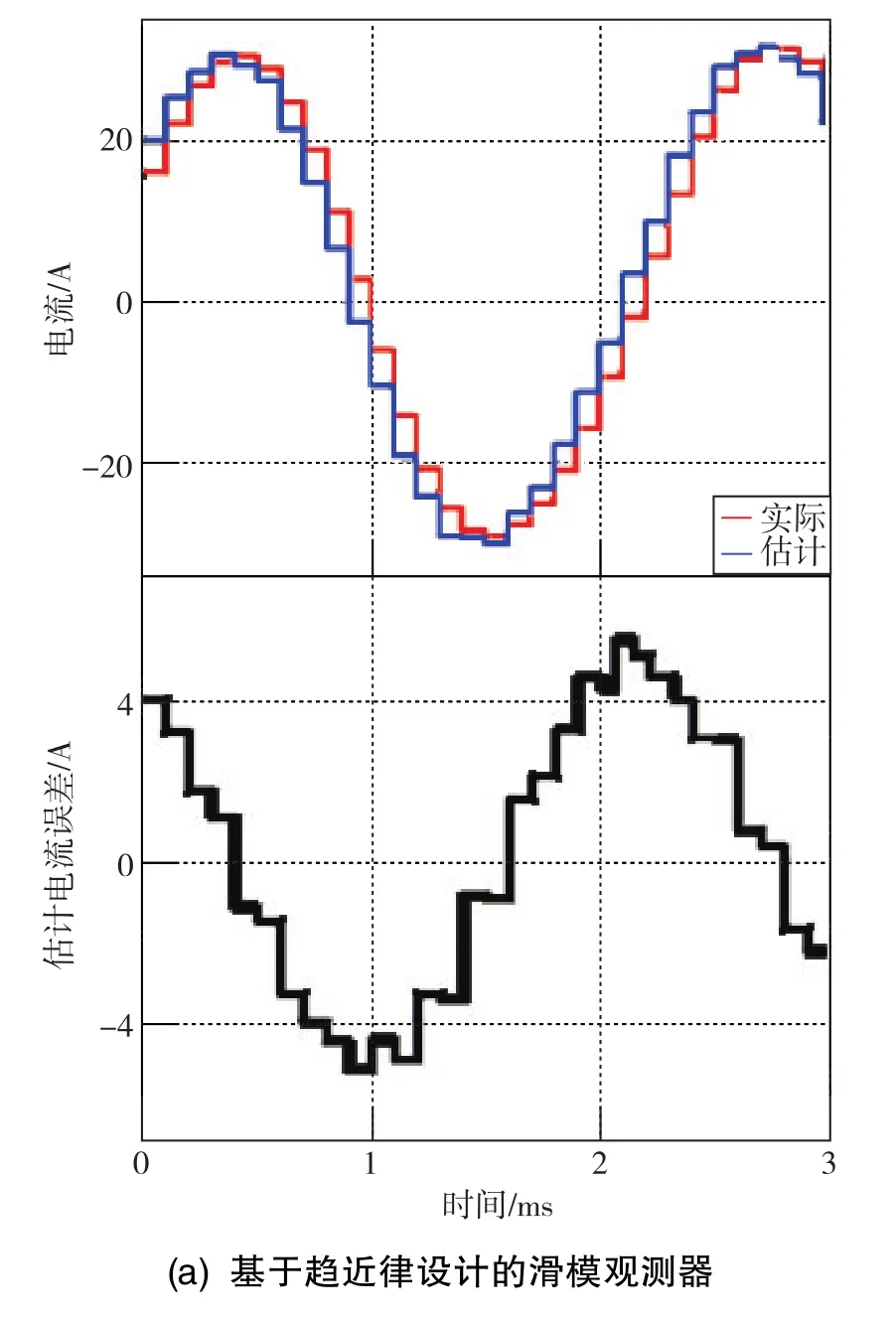
图9 定子电流α轴分量观测结果Fig.9 Observation results of stator current α-axis component

采用两种策略得到的位置信息对比如图10所示。两种策略均存在两处误差较大的位置，分别对应加速度变化的两个时刻，即开始加速和结束加速时。采用传统滑模观测器得到的位置信息，无论是速度估计误差还是角度估计误差，均存在较大抖振。在额定转速3200r／min时，角度估计误差不仅有15°的滞后，其波动的峰峰值接近了20°，其转速估计误差波动的峰峰值接近了25r／min；而基于趋近律设计的滑模观测器观测误差均在0附近，且其抖振远远小于传统滑模观测器的。

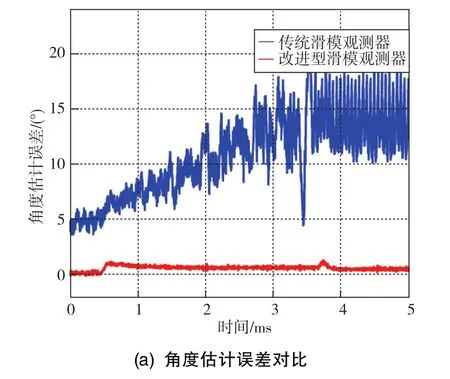
图10 两种滑模观测器的估计误差对比Fig.10 Comparison of estimation errors between two sliding mode observers

4 结论

本文提出了一种改进型离散滑模观测器来获取永磁同步电机的位置信息，采用基于趋近律设计的滑模观测器解决了传统滑模观测器的抖振问题，采用自适应反电势滤波器避免了低通滤波器所带来的相位延迟，对归一化锁相环在电机加减速过程中的稳态误差进行了分析并对其进行补偿。仿真结果表明，基于趋近律设计的滑模观测器抖振远远小于传统滑模观测器，自适应反电势滤波器输出的估计反电势与实际反电势误差在±2V以内，且不存在相位延迟。在电机加减速运行的整个过程中，观测器输出的角度估计误差在±0.4°以内，转速估计误差在±1.5r／min以内。