基于观测器的非脆弱控制研究及其在混沌系统中的应用*

张学胜 吉明明 章 伟

（上海工程技术大学 上海 201620）

1 引言

状态观测器又被称为“软传感器”，随着观测器理论的发展，基于观测器的控制近年来成为了控制领域的研究热点之一。在传统的状态反馈控制中，在传统的状态反馈控制中，通常需要假设系统的全部状态都是可获得的。然而，受制于经济与物理上的限制，在实际系统中常常无法量测到全部的系统状态。为了解决这一问题，观测器常被用来估计系统的状态值［1～6］。近年来，基于观测器的控制在许多领域都得到了应用。例如，在文献［7］中观测器被用在了柔性机械臂中，在文献［8］中观测器被用在了故障诊断中，在文献［9］中观测器被用在了输出反馈控制中，在文献［10～11］中基于观测器的控制被用在了机器人的反馈控制中，在文献［12～13］中基于观测器的控制被用在了无人机的飞行姿态控制中。

在实际控制中，许多物理系统本质上都是非线性的［14～16］。近年来，非线性系统观测器设计问题受到了广泛关注。例如，在文献［17～18］中，研究了Lipschitz非线性系统的观测器设计问题，作为Lipschitz观测器的推广，文献［19］研究了单边Lipschitz非线性系统的观测器。近年来，递增二次限制条件被引入到系统的状态估计研究之中，该条件包含经典的Lipschitz条件，扇形条件，单边Lipschitz条件等作为特例。文献［20～21］中研究了一类满足递增二次限制条件的非线性系统中的观测器设计问题。

另一方面，实际的系统控制中常常面临着各种不确定因素的干扰，这些干扰会导致系统原本设计好的控制律出现脆弱性［25］。为了解决这一问题，通常会在基于观测器的控制器的设计过程中引入非脆弱控制［22～24］。在文献［25］中，Keel等论述了非脆弱控制的必要性，他们举例说明了当干扰导致控制率律出现微小波动时，控制结果可能会出现很大的偏差，甚至导致系统的不稳定。在此基础上，Gao等在文献［26］中研究了不确定系统中的基于观测器的非脆弱控制问题。需要指出的是，针对递增二次限制非线性系统中的基于观测器的非脆弱控制的研究仍尚未有很好的研究结果。

本文考虑了递增二次限制非线性系统中基于观测器的非脆弱控制问题。首先，结合递增二次限制条件，设计了一类基于观测器的非脆弱控制器。然后，建立了确保闭环系统渐近稳定的一类线性矩阵不等式型的充分条件。最后，通过一类Lorenz型混沌系统仿真验证了本文结论的有效性。

2 系统描述及观测器设计

考虑一类不确定非线性系统：

其中x(t)∈ℝn为系统状态，q=Hx(t)，u(t)∈ℝm为控制输入，y(t)∈ℝp为可测输出，A∈Rn×n，B∈ℝn×m，C∈ℝq×n，D∈ℝq×m，G∈ℝn×l，H∈ℝl×n为已知矩阵，f(q)为满足递增二次限制条件的非线性向量值函数，如定义1所示。

定义1（递增二次限制条件［20］）针对非线性向量值函数f(q)，若存在某个已知的适当维数的对称矩阵Mδ，使得对任意的q1，q2，下面的不等式

成立，则称f(q)满足递增二次限制条件，其中对称矩阵Mδ被称为递增乘数矩阵。

针对非线性系统（1），可设计如下形式的基于观测器的非脆弱控制器：

其中∈ℝn为系统状态的估计，∈ℝp为系统输出的估计，K∈ℝm×n为控制器增益，L∈ℝn×p为观测器增益，ΔK∈ℝm×n和ΔL∈ℝn×p为扰动矩阵。

假设扰动矩阵ΔK(t)和ΔL(t)满足：

由式（1）～（3）可得，系统状态方程和误差表达式为

接下来，需要讨论闭环系统（4）的稳定性问题。为此，类似于文献［37］中的定理1，本文给出了使系统（1）趋于渐近稳定的充分条件和求解控制器增益和观测器增益的方法，如定理1所示。

那么系统（1）在基于观测器的非脆弱控制器（2）的控制下是渐近稳定的。通过求解不等式（5）可得到控制器增益观测器增益

3 在混沌系统中的仿真

混沌系统是一种典型的非线性系统，近年来在混沌保密通信领域有着许多的应用。本节中将使用文献［21］中的Lorenz型混沌系统进行仿真，该混沌系统的参数如下：

其中a(t)=cos(3t)，b(t)=1-0.3 sin(2t)，且满足a(t)≤am，b(t)≤bm。

将上述数据代入不等式（5）中，通过Matlab解线性矩阵不等式（6）可得，系统的控制器增益和观测器增益为

将数据代入系统（1）和基于观测器的控制器（2）中，通过Matlab数值软件进行仿真，可得到如图1～图4的系统状态估计与误差的仿真结果。

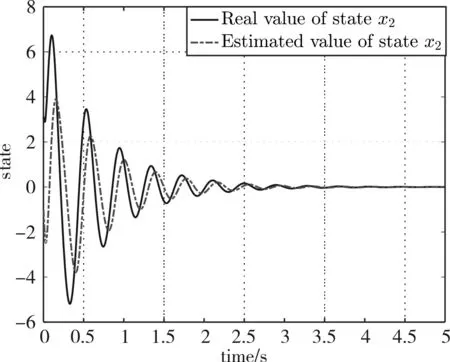
图1 系统状态x1的真实值与估计值

图2 系统状态x2的真实值与估计值

图3 系统状态x3的真实值与估计值

图4 系统状态的估计误差

由图1-图4可看出，随着时间的推移，系统的估计值逐渐趋近于真实值，系统状态的估计误差逐渐趋于零。仿真结果说明了系统（1）在基于观测器的非脆弱控制器（2）的控制下能逐渐趋于稳定。

4 结语

本文研究了一类递增二次限制类非线性系统基于观测器的非脆弱控制器的设计方法，并建立了在该控制器下闭环系统趋于渐近稳定的充分条件。最后，通过Matlab仿真将基于观测器的非脆弱控制器用在了Lorenz型混沌系统中，验证了本文提出的基于观测器的非脆弱控制器设计的有效性。