弱电网不对称故障下基于正负序解耦的锁相环设计与研究
2022-03-02马天诚黄云辉王凌云朱国荣
马天诚,黄云辉,王 栋,王凌云,朱国荣
(武汉理工大学自动化学院,湖北武汉 430070)
0 引言
风电与光伏的迅速发展促进了我国能源结构改革与电力系统的节能减排,高比例可再生能源并网将是我国电力系统发展的必然趋势[1]。为了保障新能源发电系统经逆变器和电网的稳定、高质量的能量传输,保障电力系统的稳定运行,通常使用锁相环对电网基波的频率(50 Hz)和相位进行锁定,从而实现逆变器与电网的同步运行[2-6]。
由于可再生能源的分布区域往往在距离用电中心较远的偏远地区,长距离的输电线路带来较大的阻抗并且新能源发电的渗透率不断提高,电网表现为弱电网特性[7]。通过短路比(Short Circuit Ratio,SCR)对电网强度进行定义。通常认为SCR 小于3为弱电网,小于2 为极弱电网[8-9]。在弱电网下,锁相环主导风机并网系统的程度上升,对系统稳定性影响更大[10-11]。因此有必要对弱电网下的新能源并网系统对锁相环的参数设计和性能需求进行研究。无论是对称故障还是不对称故障,都会带来电网三相电压幅值的跌落,在不对称的情况下还会有相位的突然改变。在二者改变瞬间,电网中产生的直流和谐波分量势必会对锁相环的动态产生影响,从而在对称故障下也会出现负序分量导致风机负序电流控制动作。由于不对称故障同时具有电网电压幅值和相位的突然改变,因此不对称故障下的风机控制需要对弱电网不对称故障下的锁相环进行改进和研究。
中外学者已经对锁相环进行了大量的研究。文献[12-15]提出的同步参考系锁相环(Synchronous Reference System Phase-locked Loop,SRF-PLL)结构简单,能够通过将三相电网电压转换到同步旋转坐标系下,再将q轴电压控制为0 来实现对电网电压相位的锁定。但其在电网电压不对称时会产生锁相偏差。文献[16-18]基于二阶广义积分器(Second Order Generalized Integrator,SOGI)提出的锁相环结构,比SRF-PLL 具备更好的滤波性能,能够在电压不对称时消除不对称时的谐波带来的影响,是目前应用较多的锁相环结构,但不能消除直流分量的影响问题。文献[19-21]提出一种在二阶广义积分器的基础上加入滤波环节,能够减小直流分量的影响,但是效果不理想。文献[22]提出滤波加多级并联的结构,滤波性能有所提升,但是结构比较复杂,参数设定比较困难。
为了提高在直流和谐波分量同时存在的情况下锁相环的动态性能,本文研究了一种基于四阶广义积分器(Fourth Order Generalized Integrator,FOGI)的锁相环滤波结构,能够实现对直流和谐波分量的滤除作用,从而增强锁相环的正负序解耦能力。且结构和设计参数的难度相对其他改进方法更加简单。对所研究的四阶广义积分器结构和频率特性进行分析,说明其能够具备更好的滤波性能的原因。最后通过使用Matlab 仿真软件,比较了所提出的FOGI 结构和其他解耦结构的锁相效果,在双馈风机模型中使用基于FOGI 的锁相环在不同短路比下进行了仿真研究,得到了基于FOGI 的锁相环的改进效果和适用情境。
1 传统PLL导致的问题
由于故障时电压跌落产生直流和谐波分量,而传统的锁相环解耦结构不能对直流和谐波分量进行有效地抑制,使直流分量和谐波分量对锁相结果造成影响。
1.1 电网不对称故障产生直流和谐波分量机理分析
在三相对称运行情况下,三相电网电压为式(1),三相电压经过Clark 变换到αβ坐标系为式(2),在电网发生不对称故障时,电网电压幅值U+和相位θ0发生突变时,根据傅里叶分析的原理,跌落时间电网中势必存在衰减的直流分量和谐波分量。由于三相电压的变化在不对称故障下是不对称的,因此三相电压波形跌落时所含谐波成分(Δa,Δb,Δc)是不相等的(如图1 所示),此时ΔUα,ΔUβ为谐波分量,转换到二相坐标系下,二者均不为零。
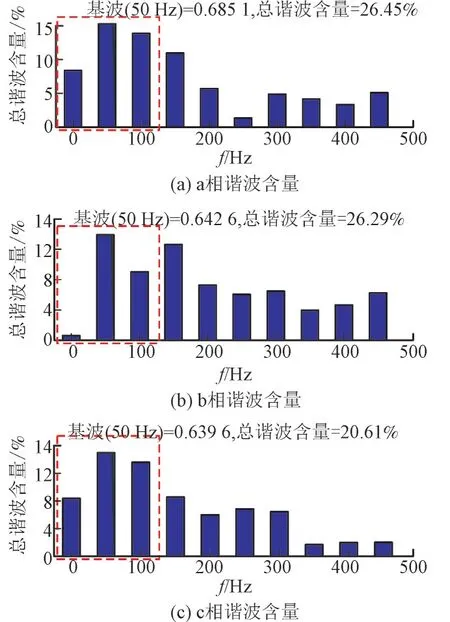
图1 故障三相电压谐波分析Fig.1 Harmonic analysis of three-phase voltage in asymmetric fault condition

式中:U+,Ua,Ub,Uc分别为电网正序电压幅值和三相电压;Uα,Uβ为两相坐标系下的电压。
在三相电压发生对称跌落时,由于三相电压互相有相位差,其电压跌落幅度不一致,导致产生的直流和谐波分量的大小也不一致。在此期间不仅正序锁相环输出的结果会产生波动,负序锁相环在对称跌落的瞬间产生一个错误动态的过程。这是在对称故障下的控制不希望发生的。
无论是对称故障还是不对称的故障,突变产生的谐波和直流分量,如果不能被解耦环节有效抑制,就会影响锁相环的锁相结果。这要求在正负序解耦环节具备将直流分量和谐波分量滤除的能力,才能使正负序分量尽可能完全解耦,保证不对称故障时双馈风机正负序控制的稳定性。
1.2 不对称故障下SOGI-PLL 导致的正负序不完全解耦问题
锁相环的解耦锁相结构有结构简单的SRFPLL、基于二阶广义积分器的SOGI-PLL、基于二阶广义微分器的SODI-PLL 以及一些改进的结构,如加入直流抑制环路来单独针对直流分量,加入串联低通滤波器等。目前应用最广泛的是基于二阶广义积分器的SOGI-PLL。
二阶广义积分器是正交信号发生器,其作用是对转换到二相静止坐标系的基波分量幅值不变并产生90°的相移,从而实现正负序的解耦分离。其结构如图2 所示,图2 所示的结构中2 个输出比输入的传递函数D(s)和Q(s)如式(4)—式(5)所示。其中,k为比例环节比例系数;ω′为谐振频率;q表示偏转90°;v和v′分别为输入和输出。
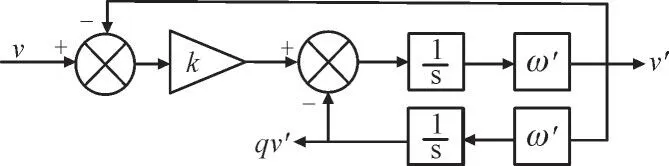
图2 SOGI结构Fig.2 Structure of SOGI
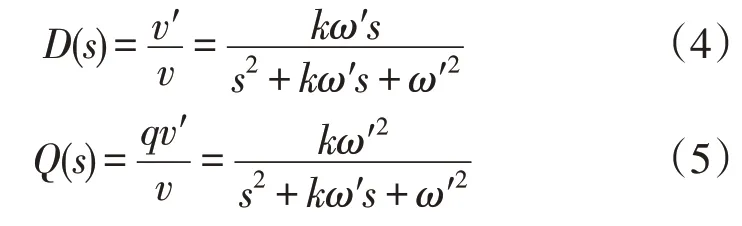
在本文中由于基波频率为50 Hz,所以对应的谐振频率应为100 π。SOGI 的BODE 图如图3 所示。

图3 SOGI的BODE图Fig.3 Bode diagram of SOGI
从图3 可知,二阶广义积分器能够对除了基波之外的谐波分量有滤除作用。但是其产生90°相移的部分不具备对直流分量的滤除作用。其他类型的锁相环结构,同样是通过其本身的滤波特性对基波保留,对谐波滤除来完成对电网电压的正负序解耦。
因此在不对称故障时,同时产生正负序的电压的波动产生的直流分量会相互影响正负序锁相环的锁相结果,未能实现正负序完全解耦。
1.3 弱电网下传统PLL引起的系统稳定性问题
锁相环检测并网点电压,来获取电网电压的频率和相位来同步电网频率,为变换器控制系统提供同步基准。因此锁相环的动态性能会影响并网逆变器的能量传输的控制,进而影响并网点电压。在电网强度较弱的情况下,锁相环带宽对并网系统的稳定性的影响将更加明显[23-24]。
依据文献[25]提出的双馈风力发电机数学模型及其建立的弱电网下双馈风力发电系统的小信号模型,本文采用特征值分析法对连接弱电网的双馈风机动态稳定性展开分析。改变锁相环的带宽,从6—24 Hz 研究锁相环在弱电网下对双馈风机并网系统的稳定性影响。得到双馈风机并网系统的特征根分析图,如图4 所示,其中,*×均为系统的特征根,沿着箭头方向系统锁相环带宽从6—24 Hz 变化。
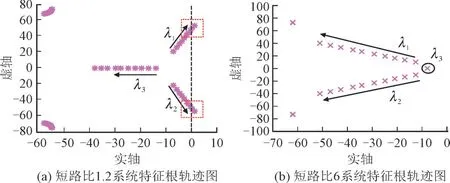
图4 锁相环带宽变化特征根分析Fig.4 Characteristic root analysis of phase-locked loop bandwidth variation
图4(a)中λ1,λ2为主导特征根,对应风机锁相环模态。随着锁相环的带宽从6 Hz 到24 Hz 变化,特征根λ1到λ2向右移动,在锁相环带宽达到20 Hz之后λ1到λ2越过零轴,系统开始不稳定。可见在弱电网下随着锁相环带宽的增加,双馈风机并网系统的稳定性逐渐降低,甚至导致系统不稳定。在图4(b)中,在强电网下,随着锁相环带宽的改变,锁相环模态对应的特征根λ1到λ2逐渐左移,λ3对应的端电压环在此时主导双馈风机并网系统的稳定性,且锁相环的带宽改变几乎不对其产生影响,整个所有极点均处于零轴左侧。此时锁相环带宽的改变对系统稳定性几乎没有任何影响。说明锁相环在弱电网下主导双馈风机并网系统的稳定性。
根据图4(a),随着带宽变大,锁相环响应速度变快,系统稳定性变差,在弱电网下的双馈风机并网系统对锁相环的要求是较小的锁相环带宽、较慢的响应速度。根据图4(b),在强电网下的锁相环,在带宽较大、锁相环响应速度较快时系统整体特征根向左移动,稳定性变好,在强电网下的双馈风机并网系统对锁相环的要求是较大的锁相环带宽、较快的响应速度。
2 FOGI-PLL的分析和参数设计
2.1 弱电网不对称故障下FOGI-PLL的特性分析
为了改善二阶广义积分器的滤波性能,能够对电网在发生不对称故障时对直流分量有更好的滤除作用,获得更好的正负序解耦能力,对SOGI 滤波结构进行改善。图5 为在SOGI 的基础上进行改进的FOGI 结构。其中,K1,K2为比例系数;ω′为谐振频率;v和v′分别为输入和输出;q表示偏转90°。
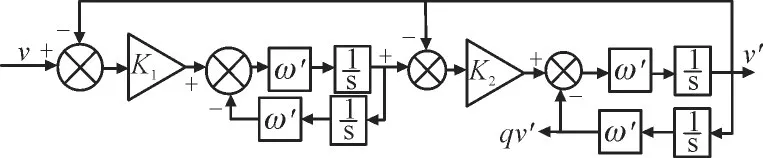
图5 FOGI结构Fig.5 Structure of FOGI
对比二阶广义积分器,FOGI 采用2 个二阶广义积分器的串联结构,具备更好的滤波效果。式(6)和式(7)分别为图5 中2 个输出比输入的传递函数。

设置ω′为100 π,得到FOGI 的特性曲线,如图6 红色线所示。从图6(a)可知,对谐振频率的50 Hz基波分量的相移90°是适用且能够实现对电网电压的正负序分离。对于谐波分量的滤除作用更好。在零频处的增益大大降低了,FOGI 能够对直流分量有滤波作用。

图6 FOGI&SOGI对比Fig.6 Comparison of FOGI and SOGI
在不对称故障时,正负序不完全解耦问题导致的电网电压正负序之间波动产生的直流和谐波分量能够被更有效地抑制。在不对称故障下,对电网电压正负序解耦和锁相更加精确,有利于不对称故障下的双馈风机的控制。
图7 为不同滤波解耦结构在不同锁相环带宽下的特征根对比图,其中,沿着箭头方向系统锁相环带宽度从6—24 Hz 变化。
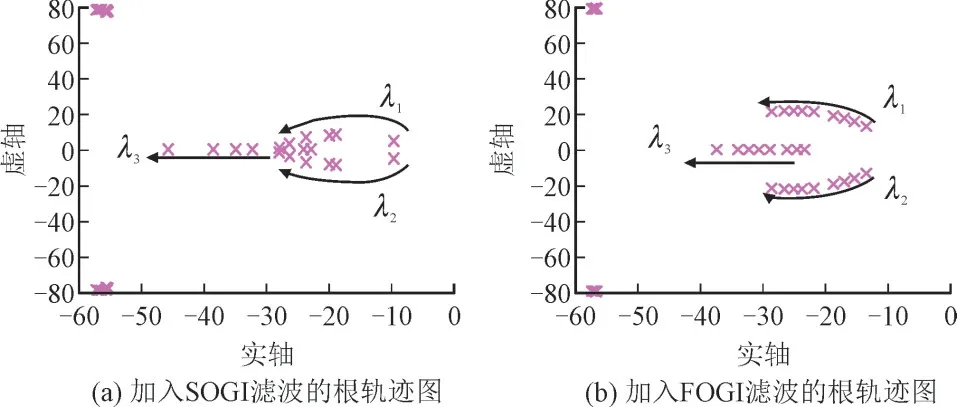
图7 加入FOGI&SOGI滤波解耦对比(SCR=1.2)Fig.7 Comparison of Characteristic root between FOGI and SOGI filtering decoupling structure(SRC=1.2)
根据1.3 节的弱电网下双馈风机并网系统对锁相环的性能需求分析,FOGI 较慢的响应速度有利于整个系统的稳定性。在未加入SOGI 解耦滤波环节之前,在锁相环带宽逐渐变大时,特征根出现越过零轴,系统存在由稳定到不稳定的变化趋势。在图7(a)中整个过程中系统所有特征根不存在越过零轴的现象,系统始终是稳定的,可见系统稳定性变好。而加入FOGI 解耦滤波环节之后,由图7(a)和图7(b)的对比可知,锁相环模态对应的特征根λ1,λ2进一步向左移动,系统稳定性变好。
使用FOGI 滤波解耦环节比传统的使用SOGI滤波解耦环节的锁相环更适用于弱电网下的情况,能够使双馈风机并网系统在弱电网情况下获得更好的稳定性。
2.2 FOGI-PLL的参数选择
FOGI-PLL 结构中的比例系数会直接影响其滤波性能,本节通过分析其滤波特性,来选择合适的参数获得较好的滤波性能。图8 为不同参数FOGI的滤波特性图。
从图8(a)和图(b)可知,随着K1的增大逐渐出现2 个谐振尖峰,在K1较小的时候也有1 个谐振峰的出现。谐振会造成系统震荡甚至是不稳定。从图8(c)和图(d)可知,在K2较小时滤波性能不如K2较大时,但是随着滤波性能提升,在基频50 Hz 处出现2 个峰,会对系统稳定性产生影响。综合考虑滤波性能和系统稳定性,选择根K1=。
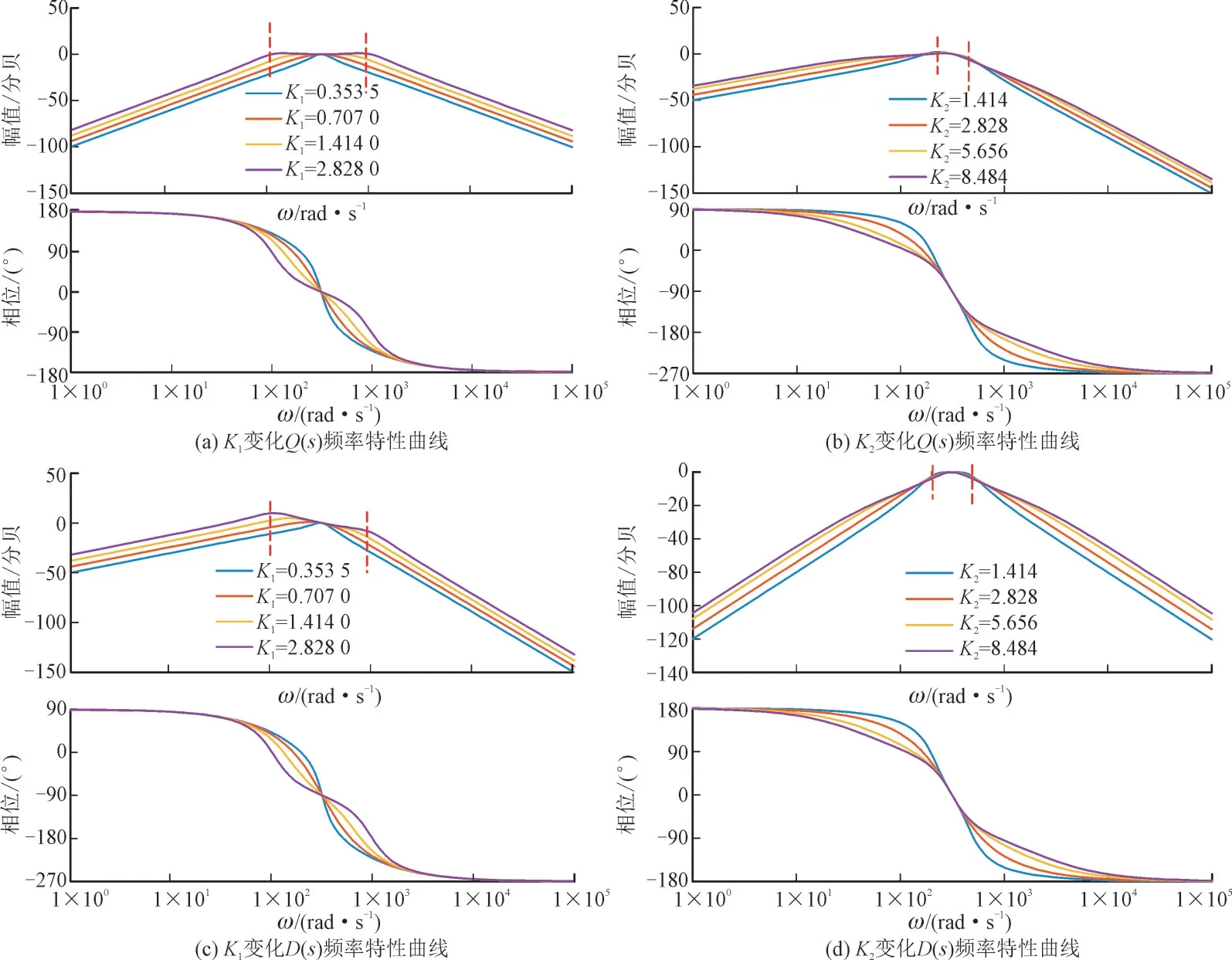
图8 K1、K2参数选择Fig.8 Diagram showing selection of K1 and K2
3 传统SOGI-PLL和FOGI-PLL的对比
为验证本文所提分析结果,利用Matlab 仿真软件进行仿真实验。仿真内容分为3 部分:(1)Matlab中三相电压源模拟电网发生对称故障时的锁相环动态;(2)Simulink 中时域双馈风机并网模型在同一弱电网下单相对地短路时比较SOGI 和FOGI 的锁相环动态;(3)使用FOGI 滤波解耦环节的锁相环在强弱电网下的锁相环动态比较。
图9 为在理想电压源发生对称故障时,分别使用SOGI 和FOGI 锁相环的动态表现。

图9 电压对称跌落锁相环动态Fig.9 PLL dynamics during voltage symmetrical drop
从图9 可知,锁相环的动态单纯由电压幅值跌落而产生的直流分量和谐波分量影响,没有相位突变的影响。使用FOGI 滤波解耦环节的锁相环的正负序输出频率的波动更小,但是响应速度较慢。
图10 为双馈风机连接短路比为2.16 的弱电网的正负序锁相环动态。
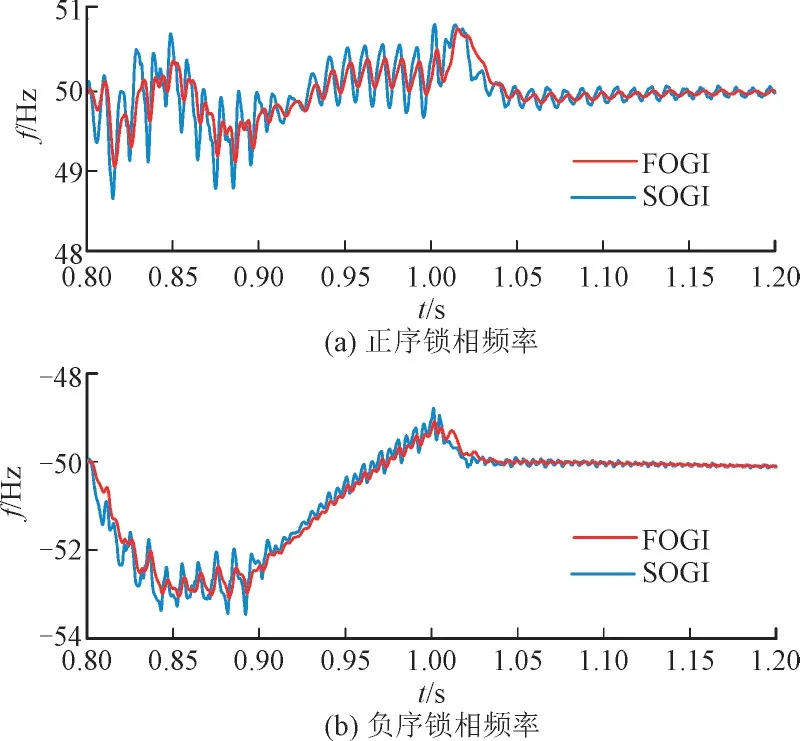
图10 不对称故障DFIG锁相环动态Fig.10 PLL dynamics of DFIG during asymmetric faults
不对称故障状态时电网电压的幅值和相位都发生了突变。从图10 可知使用FOGI 的频率波动的峰值更小但是在故障恢复的过程中锁相速度较慢,较慢于SOGI 稳定。
图11(a)和图11(b)分别为使用FOGI 滤波解耦环节和使用SOGI 滤波解耦环节的锁相环在不同短路比下的锁相环动态。

图11 不同短路比下锁相环动态Fig.11 PLL dynamics with different short circuit ratio
从图11 可知,在各个短路比下FOGI 的锁相环输出的频率波动都小于SOGI 的锁相环;图11(a)中随着电网强度变弱,振荡的峰值变大,但是在电网强度最弱的绿色线从第2 个峰开始,波动明显最小,到最后最先稳定。说明FOGI 滤波解耦结构更适用于弱电网的情况。从图11(b)可知SOGI 滤波解耦结构在较强的电网强度情况下更适用。
4 结论
本文分析了弱电网下锁相环对双馈风机并网系统的稳定性的影响、传统锁相环不完全解耦问题的产生机理和传统锁相环不适用于弱电网不对称故障的原因,研究了一种基于四阶广义积分器(FOGI)滤波解耦的锁相环结构。通过数学分析和仿真验证得到如下结论:
1)弱电网不对称故障时新能源发电系统端电压相位和幅值突变产生直流和谐波分量,并导致传统锁相环正负序解耦不完全,甚至会引起不稳定的问题。
2)基于四阶广义积分器的锁相环比传统锁相环对直流分量和谐波分量具备更好的滤波性能,并且比传统锁相环更有利于于弱电网的稳定。
3)基于四阶广义积分器的锁相环的比传统锁相环有更优越的正负序解耦能力,从而能够更好应用于弱电网下发生不对称故障时的控制。
