外转子交替极伺服永磁电机低转矩脉动设计与综合优化

梁泳涛，贾少锋，梁得亮

（西安交通大学电力设备电气绝缘国家重点实验室，西安 710049）

0 引言

伺服系统用于精确、连续地控制被控对象的转角或位移，在机械制造、军事应用等领域有着广泛的应用。永磁电机由于其结构简单、转矩脉动小等优势，已经成为伺服驱动的主要发展方向[1]。同时，由于稀土永磁材料性能优异，采用钕铁硼等稀土永磁的永磁电机具有高效率、高功率密度的优点，在伺服系统等领域得到了广泛应用[2]。但是，由于近年来稀土开采相关保护政策的实施，导致稀土价格上涨。因此，许多学者开展了关于 “少稀土电机” 的研究[3-4]。交替极永磁（Consequent-pole Permanent Magnet， CPPM）电机相较于常规永磁电机仅有一半的永磁体数量，其能够大幅提高永磁体的利用率，减少永磁体用量。因此，交替极结构在横向磁通永磁电机[5]、磁通反向永磁电机[6]、表贴永磁电机[7-8]、永磁游标电机[9]等电机中得到了广泛应用。

在伺服驱动系统中，电机的转矩脉动会对电机的伺服控制性能和控制精度产生很大的影响，是其最关注的性能指标之一。从电机本体考虑，目前针对永磁电机的转矩脉动可以采用斜槽、开辅助槽、磁极形状优化、极弧系数组合等方式进行优化[10]。交替极电机由于存在不对称气隙磁场[11]，将对交替极电机的齿槽转矩[12]、反电势波形和电磁转矩脉动[13]造成影响，使得交替极电机的转矩脉动相较常规永磁电机更显著。文献[14]对不同槽极配合下交替极电机的齿槽转矩和转矩脉动进行了研究。文献[15]和文献[16]提出了N-S-铁-S-N-铁和Spoke-面贴式混合极新型转子结构，以消除气隙磁密偶次谐波导致的电磁转矩脉动。总的来说，目前国内外学者针对CPPM电机的转矩脉动抑制研究仍然有限[17]。因此，对CPPM电机进行转矩脉动综合优化具有重要意义。

本文首先对CPPM电机转矩脉动的产生原因与优化机理进行分析，通过槽极数配合、优化极弧系数、永磁体不等极弧系数与定子齿偏心等方法对外转子交替极伺服电机转矩脉动进行综合优化设计，随后运用有限元软件对电机进行仿真分析，仿真结果验证了优化方法的有效性，最后制作了样机。

1 CPPM电机转矩脉动的产生机理

对于永磁同步电机来说，转矩脉动主要由齿槽转矩和纹波转矩两部分组成。其中，齿槽转矩由齿槽效应引起，永磁体产生的磁场与电枢铁芯的齿槽相互作用，使得电机转子和定子有沿某一方向对齐的趋势；而纹波转矩主要由电机电流的时间谐波和气隙磁密的空间谐波造成，电机绕组分布的不正弦、电机电枢反应的影响、逆变器元件性能等因素都会使电机电流和反电势波形畸变，导致电机的转矩脉动[18]。

CPPM电机通过将传统永磁电机中所有N极（或S极）用铁芯代替，构成铁芯凸极与永磁体交替出现的结构，其铁芯凸极受到永磁体磁化呈现出与永磁体相反的极性。CPPM电机转矩产生的机理与传统永磁电机相同，因此转矩脉动产生的原因也与传统永磁电机类似。但是对于CPPM电机而言，由于其结构的特殊性，电机的齿槽转矩相比相同槽极配合的传统永磁电机更加明显。除此之外，一些分数槽电机会因CPPM电机转子结构导致气隙磁密不平衡，使得反电势存在偶次谐波，增加了电机的转矩脉动[10]。

2 CPPM电机转矩脉动的优化机理

2.1 永磁体不等极弧系数优化机理

在不考虑磁路饱和、电机铁芯的磁导率为无穷大、永磁体与空气的磁导率相同、永磁体中的磁场能量保持不变等理想条件下，通过能量法可以计算出CPPM电机的齿槽转矩表达式

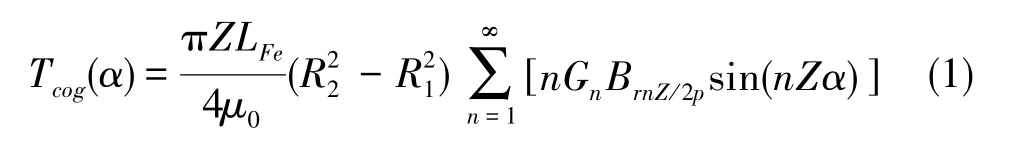
式（1）中，LFe为电机轴向长度， R1和R2分别为转子内径和定子外径，n为使得nZ／2p为整数的最小整数[10]。

由式（1）可知， BrnZ／2p和 Gn为影响齿槽转矩的主要因素。齿槽转矩的削弱可以从减小气隙磁导、永磁体剩磁磁密的谐波次数和幅值的角度入手。

采用永磁体不等极弧系数设计的CPPM电机转子结构如图1所示，永磁体不等极弧CPPM电机样机部件如图2所示。由图1可知，电机转子中不同宽度的永磁体交替分布，PM1和PM3的极弧系数为αpm1，PM2和PM4的极弧系数为αpm2，铁芯凸极的极弧系数为αi。

图1 非对称磁极交替极外转子拓扑结构Fig.1 Topology of the CPPM motor outer rotor with asymmetrical PM poles

图2 采用永磁体不等极弧设计的CPPM电机样机部件Fig.2 Prototyping components of CPPM motor with asymmetrical PM poles

永磁体不等极弧CPPM电机的气隙磁密如图3所示，Brm为永磁体所对应的气隙磁密幅值，Bri为铁芯对应的气隙磁密幅值。

图3 非对称磁极CPPM电机的气隙磁密分布Fig.3 Air-gap flux density of CPPM motor with asymmetrical PM poles

为了计算永磁体不等极弧CPPM电机的齿槽转矩，对CPPM电机气隙磁密的平方进行Fourier展开，并求取Fourier系数Brh[17]

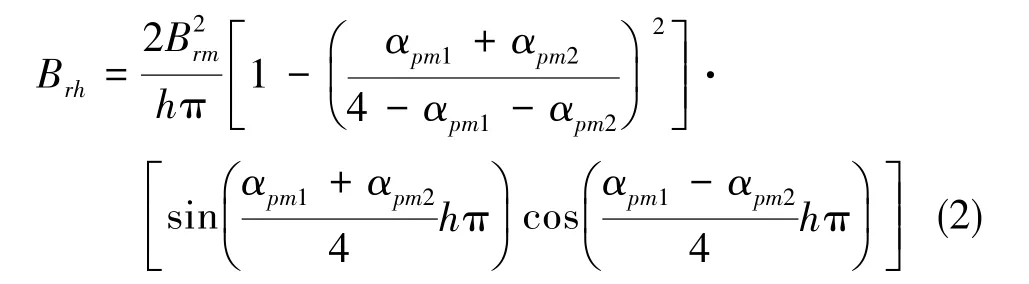
对比式（1）， 只有 h=nZ／2p（n=1， 2， 3， …）次Fourier分解系数才对齿槽转矩起作用。因此，合理选择CPPM电机不等极弧系数设计中的参数αpm1、 αpm2与αpi， 可减小气隙磁密中的nZ／2p次谐波，从而减小电机齿槽转矩，实现CPPM电机转矩脉动的优化。

2.2 定子齿偏心结构优化机理

图4为定子齿偏心结构的示意图，h为定子齿偏心距，当采用偏心结构后，定子齿顶圆弧所对应的圆心由原先的O点向上移动h距离到了O′点处。定子齿偏心结构通过优化定子铁芯外表面极弧形状从而达到减小气隙磁密谐波含量、抑制电机转矩波动的目的，图5为采用定子齿偏心结构的CPPM样机定子示意图。

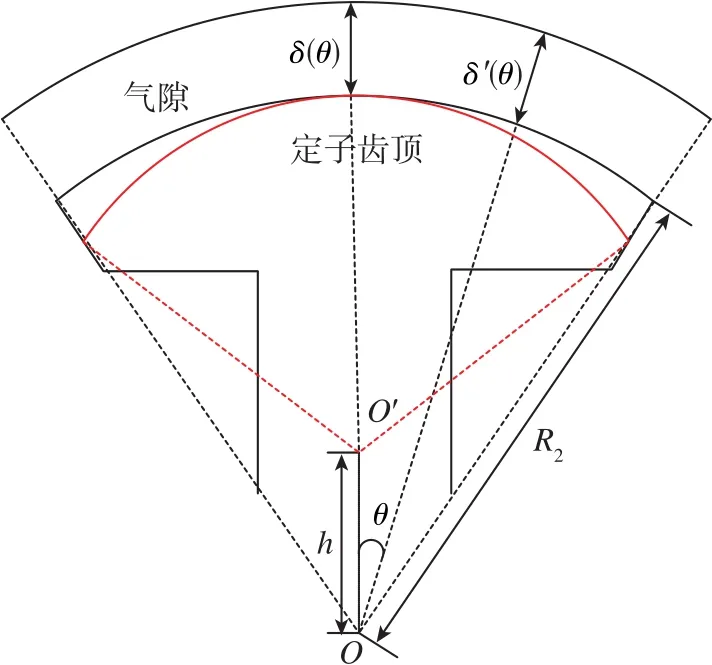
图4 定子齿偏心结构示意图Fig.4 Schematic diagram of stator tooth eccentric structure

图5 定子齿偏心结构的CPPM样机定子Fig.5 Schematic diagram of CPPM motor stator with stator tooth eccentric structure

传统电机的气隙磁密分布表达式为

式（3）中， hm为永磁体充磁方向长度， Br（θ)、δ（θ，α)分别为永磁体剩磁、有效气隙长度沿圆周方向的分布。

定子齿偏心结构电机的气隙磁密分布表达式为

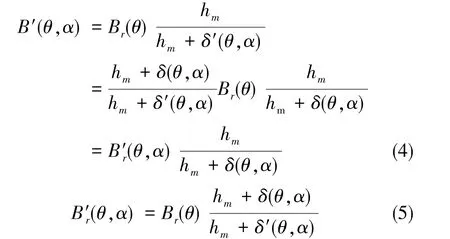
通过数学变换， 只需将 B′r（θ， α）的平方进行Fourier展开，求出相应的Fourier系数，就可以代入齿槽转矩的计算公式中进行计算。

通过图4可求出定子齿顶对应的气隙长度，其表达式为

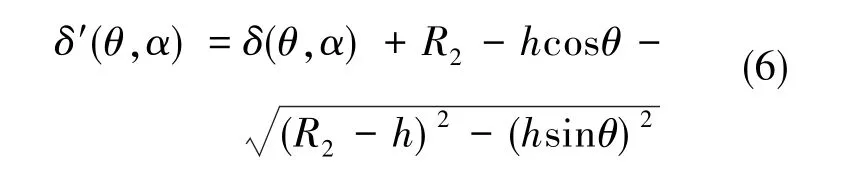
将式（6）代入式（5）中，可以得到永磁体剩磁磁密平方的表达式[19]

式（7）中，t（θ，α）=[hm+δ（θ，α）]／R2，b=h／R2。

3 仿真模型的建立

实际情况下，CPPM电机的气隙结构较为复杂，且上述优化方法的理论分析是在一定的理想条件下进行的，因此需要运用有限元方法对电机性能做进一步的分析。

本文中的交替极永磁电机的设计要求为300r／min、63W，考虑到电机槽极配合对转矩脉动的影响，电机的槽数与极数的公倍数越大，电机的齿槽转矩就越小。本文电机的槽极数选用18槽20极，绕组采用双层分布式集中绕组。为了研究优化极弧系数、永磁体不等极弧、定子齿不等宽等方法对CPPM电机转矩脉动优化的效果，使用有限元软件建立了4种电机模型，如图6所示。图6（a）为18槽20极传统表贴式永磁（SPM）电机，图6（b）为18槽20极的CPPM电机，图6（c）中的CPPM-1电机采用了永磁体不等极弧的设计，图6（d）中的CPPM-2电机同时采用了永磁体不等极弧以及定子齿偏心的设计。4种不同电机的定转子内外径、气隙长度、叠片长度等参数相同，电机定转子均采用牌号为DW310-35的硅钢片，磁钢材料牌号为N35的永磁体，电机的主要参数如表1所示。

图6 18槽20极永磁电机不同结构的截面图Fig.6 Cross section of 18-slot／20-pole machines with different structures

表1 18槽20极电机主要设计参数Table 1 Main design parameters of 18-slot／20-pole machines

4 电机转矩脉动的优化

本文使用Ansys Maxwell软件进行有限元分析，电机采用id=0的控制策略，不同的电机模型均通入相同的电流。

4.1 永磁体极弧系数的优化

极弧系数是影响永磁电机齿槽转矩的重要因素之一，合理地选择电机永磁体极弧系数能够降低电机的齿槽转矩和转矩脉动。在电机其他参数不变的情况下，SPM电机与CPPM电机的平均转矩和转矩脉动随着永磁体极弧系数的变化关系如图7所示。在计算SPM电机极弧系数αspm与CPPM电机极弧系数αcppm的过程中，二者对应的极距所跨弧度均为π／10。由图7可知，αspm在0.80～0.99变化时，SPM电机的平均转矩随着αspm的增加而增加，αspm=0.93时， 电机转矩脉动最小， 为2.17%；αcppm在1.00～1.20变化时，CPPM电机的平均转矩同样随着αcppm的增加而增加，当αcppm=1.09时，电机转矩脉动最小，为6.29%。

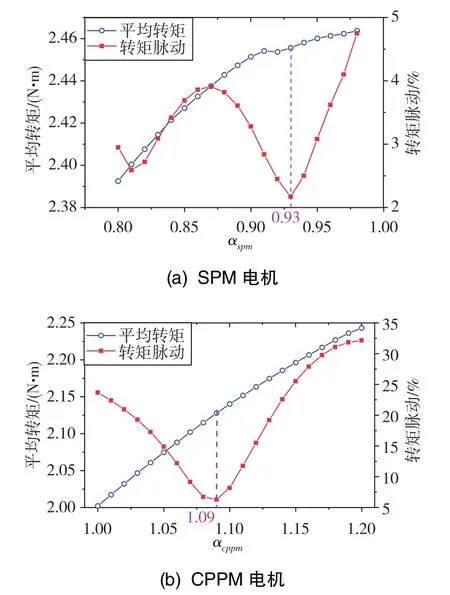
图7 SPM电机与CPPM电机平均转矩和转矩脉动随永磁体极弧系数的变化关系Fig.7 Variations of average torque and torque ripple withαspmandαcppmfor SPM motor and CPPM motor

选取αspm=0.93与αcppm=1.09， 对SPM电机与CPPM电机的性能作进一步分析。

SPM电机与CPPM电机的负载磁密分布如图8所示。由图8可知，CPPM电机永磁体与硅钢片相互接触的部分漏磁较为明显。同时，在选取αspm=0.93与αcppm=1.09的情况下，CPPM电机的永磁体用量仅为SPM电机的59.6%，CPPM定子齿部的磁密比SPM电机低。图9展示了SPM电机与CPPM电机空载气隙磁密的波形与FFT结果，二者空载气隙磁密所含主要谐波均为奇次谐波，SPM电机空载气隙磁密基波幅值要大于CPPM电机，且空载气隙磁密的畸变更小。电机空载反电势波形和FFT对比如图10所示。由图10可知，SPM电机的空载相反电势基波幅值大于CPPM电机，分别为22.9V与20.0V。同时，SPM电机的相反电势的畸变更小。从以上仿真结果可以推测，相较于SPM电机，CPPM电机气隙磁密和反电势波形的畸变更大，会导致其出现较大的转矩脉动。

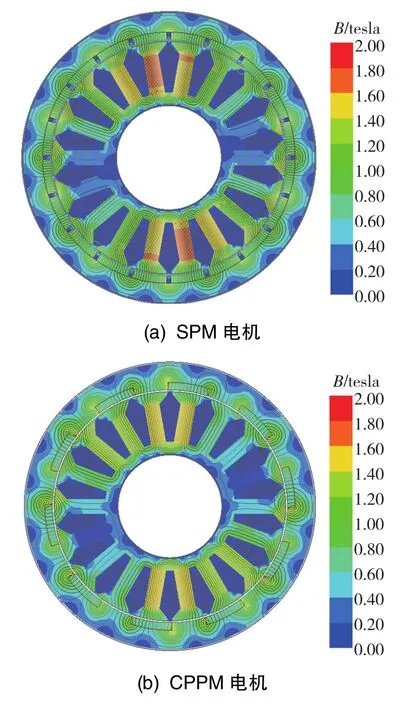
图8 SPM电机与CPPM电机的负载磁密分布Fig.8 Load flux distribution of SPM motor and CPPM motor

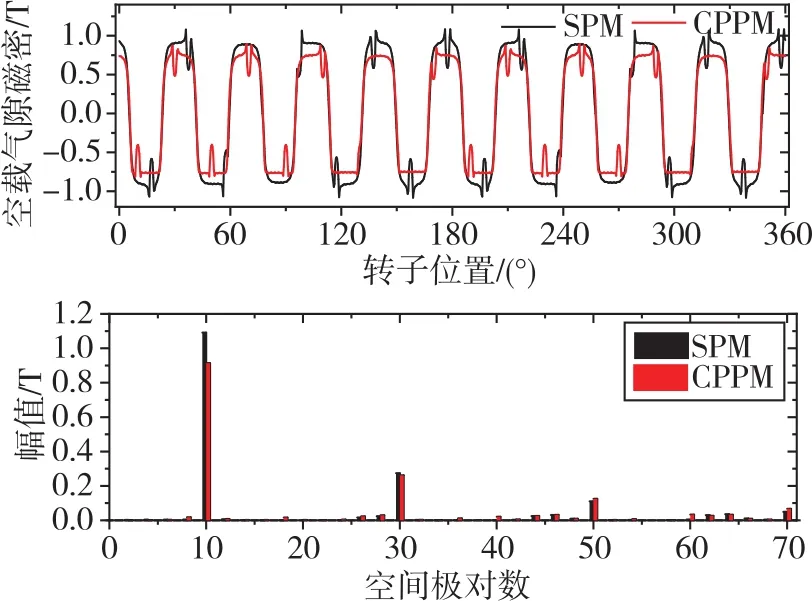
图9 SPM电机与CPPM电机空载气隙磁密波形及FFT分析对比Fig.9 Analysis and comparison of the open circuit air-gap flux density waveform and FFT between SPM motor and CPPM motor

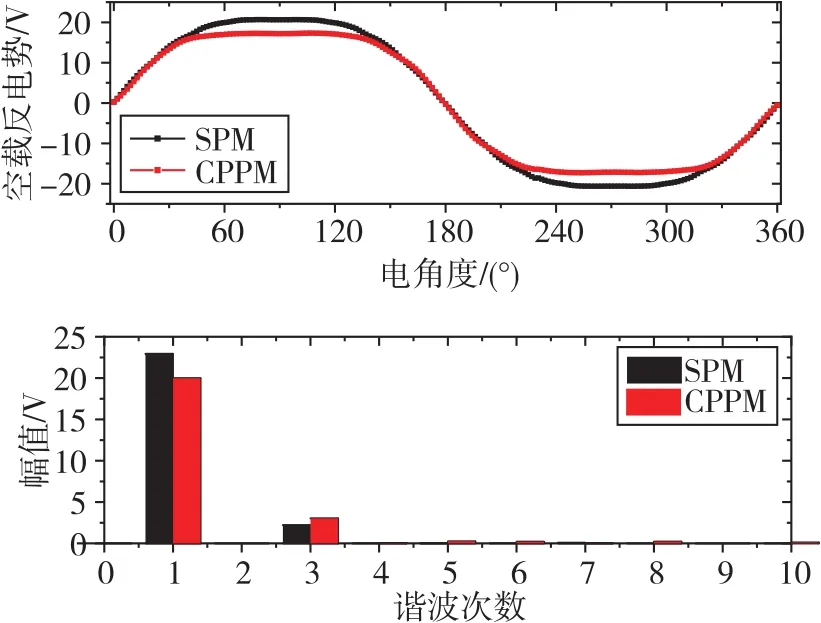
图10 SPM电机与CPPM电机空载反电势波形及FFT分析对比Fig.10 Analysis and comparison of the back-EMF waveform and FFT between SPM motor and CPPM motor at open circuit condition

图11和图12分别为SPM电机与CPPM电机的齿槽转矩和转矩的波形对比。可以看到，SPM电机与CPPM电机的齿槽转矩峰峰值分别为17.0mN·m、98.6mN·m。经计算，两个电机的平均转矩和转矩脉动分别为2.46N·m、2.13N·m和2.17%、6.29%。相较于SPM电机，CPPM电机的齿槽转矩谐波次数更小，齿槽转矩更明显，转矩脉动也更严重。

图11 SPM电机与CPPM电机的齿槽转矩波形对比Fig.11 Comparison of cogging torque waveform between SPM motor and CPPM motor

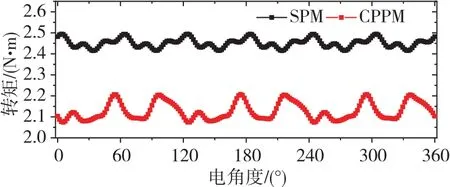
图12 SPM电机与CPPM电机的转矩波形对比Fig.12 Comparison of torque waveform between SPM motor and CPPM motor

通过以上对比可以得出，相较于SPM电机，CPPM电机仅使用了59.6%的永磁体，却产生了86.6%的转矩，证明了CPPM电机能够节约永磁体用量。但是另一方面，CPPM电机转矩脉动相较SPM电机明显增大。通过永磁体极弧系数优化的方法，使得CPPM电机的转矩脉动有所改善，但仍需进一步优化。

4.2 永磁体不等极弧系数

通过第2章中的推导可知，采用永磁体不等极弧的方式可以进一步优化CPPM电机的转矩脉动，建立的有限元模型如图6（c）所示。CPPM-1电机中磁钢极弧系数分别为αpm1、αpm2， 相邻大小不等的磁钢交替排列。在电机其他参数不变的情况下，图13给出了αpm1与αpm2不同取值时CPPM-1电机平均转矩和转矩脉动的变化情况。由图13（a）可知，从左下角到右上角，CPPM-1电机的平均转矩随着永磁体极弧系数的上升而增加。图13（b）反映了存在多个不同的不等极弧系数组合可以使得CPPM-1电机转矩脉动较低。综合考虑电机永磁体用量、平均转矩和转矩脉动情况，使电机在较少永磁体用量的情况下输出较高的转矩，且转矩脉动较低，最终选取CPPM-1电机的永磁体极弧系数为 αpm1=1.02与 αpm2=1.20。

图13 αpm1与αpm2变化对CPPM-1平均转矩和转矩脉动的影响Fig.13 Variations of average torque and torque ripple withαpm1andαpm2for CPPM-1

对αpm1=1.02与αpm2=1.20配合下CPPM-1电机的性能做进一步分析，并将其与CPPM电机性能对比。CPPM电机与CPPM-1电机空载气隙磁密波形和FFT对比如图14所示，电机空载反电势波形和FFT对比如图15所示。

图14 CPPM电机与CPPM-1电机空载气隙磁密波形及FFT分析对比Fig.14 Analysis and comparison of the open circuit air-gap flux density waveform and FFT between CPPM motor and CPPM-1 motor

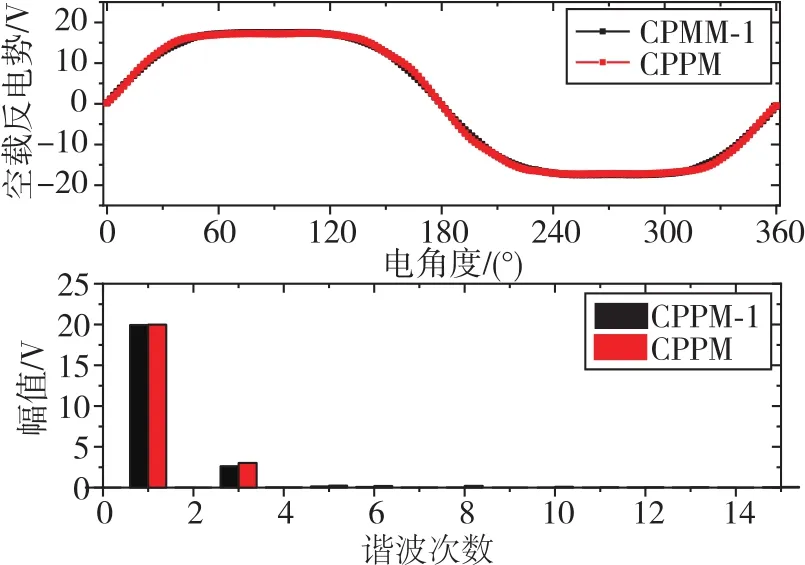
图15 CPPM电机与CPPM-1电机空载反电势波形及FFT分析对比Fig.15 Analysis and comparison of the back-EMF waveform and FFT between CPPM motor and CPPM-1 motor at open circuit condition

如图14所示，相较于CPPM电机，CPPM-1电机气隙磁密的基波幅值基本不变，3次谐波含量略有降低。此外，由于CPPM-1电机采用了大小各5块磁钢交替分布的转子结构，其气隙磁密会在空间中分解出5对极及5对极倍数的磁密，但是并不会在绕组中感应出相应次数的反电势。图15为两电机的反电势对比，可以看出，二者的反电势基波幅值基本相同，相较于CPPM电机，CPPM-1电机反电势的3、6、8次谐波含量减少。

为了验证永磁体不等极弧方法的优化效果，图16和图17分别给出了CPPM-1电机的齿槽转矩和转矩波形（蓝色曲线）。可以看出，CPPM-1电机的齿槽转矩峰峰值为24.1mN·m。经计算，CPPM-1电机的平均转矩和转矩脉动为2.12N·m、3.97%。相较于CPPM电机，在平均转矩变化不大的基础上，CPPM-1电机的齿槽转矩和转矩脉动均得到了明显的改善。

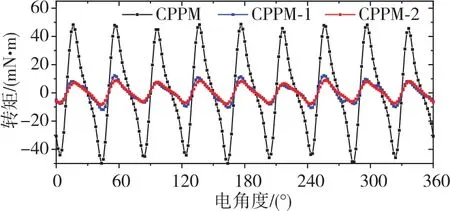
图16 CPPM电机、CPPM-1电机和CPPM-2电机的齿槽转矩波形对比Fig.16 Comparison of cogging torque waveform among CPPM motor，CPPM-1 motor and CPPM-2 motor

图17 CPPM电机、CPPM-1电机和CPPM-2电机的转矩波形对比Fig.17 Comparison of torque waveform among CPPM motor，CPPM-1 motor and CPPM-2 motor

4.3 定制齿偏心

为进一步降低电机的转矩脉动，CPPM-2电机采用了定子齿偏心结构，电机的截面图如图6（d）所示。在电机其他参数不变的情况下，图18给出了CPPM-2电机平均转矩和转矩脉动随着定子齿偏心距h的变化关系。可以看出，随着h在1mm～23mm内增加，CPPM-2电机的平均转矩逐渐减小，转矩脉动先增大后减小。当h=16mm时，转矩脉动达到最小值，此时的平均转矩和转矩脉动为2.01N·m、 2.76%。

图18 CPPM-2电机的平均转矩和转矩脉动随定子齿偏心距的变化Fig.18 Variations of average torque and torque ripple with h for CPPM-2

当偏心距h=16mm时，对CPPM-2电机的其他电磁性能进行进一步仿真。CPPM-1电机与CPPM-2电机的负载磁密分布如图19所示。可以看到，定子齿偏心结构会对电机磁力线的分布造成一定的影响。由于偏心结构导致定子齿边缘附近的磁阻增大，少量磁力线会经过气隙穿过相邻定子齿。同时，定子齿边缘气隙增大也会使得磁力线流经路径变长，气隙处的磁压降增加，影响齿部磁通量，所以CPPM-2电机齿身部的磁密要小于CPPM-1电机。在图20所示的CPPM-1电机与CPPM-2电机空载气隙磁密波形及FFT分析对比图中可以进一步验证偏心结构对电机的影响。CPPM-2电机与CPPM-1电机的气隙磁密谐波次数基本一致，但是CPPM-2电机的气隙磁密基波以及3、5、7次谐波幅值要明显低于CPPM-1电机。可以推测CPPM-2电机的平均转矩要低于CPPM-1电机，但由于气隙磁密谐波含量的减少，其转矩脉动也会有所降低。图21为CPPM-1电机与CPPM-2电机空载反电势波形和FFT对比图。由于电机空载反电势是相应次数的气隙磁密在绕组中感应得到，因此图21的规律与图20基本一致。对比CPPM-1电机，CPPM-2电机反电势基波与3、5次谐波均有所减少。

图19 CPPM-1电机与CPPM-2电机的负载磁密分布Fig.19 Load flux distribution of CPPM-1 motor and CPPM-2 motor

图20 CPPM-1电机与CPPM-2电机空载气隙磁密波形及FFT分析对比Fig.20 Analysis and comparison of the open circuit air-gap flux density waveform and FFT between CPPM-1 motor and CPPM-2 motor

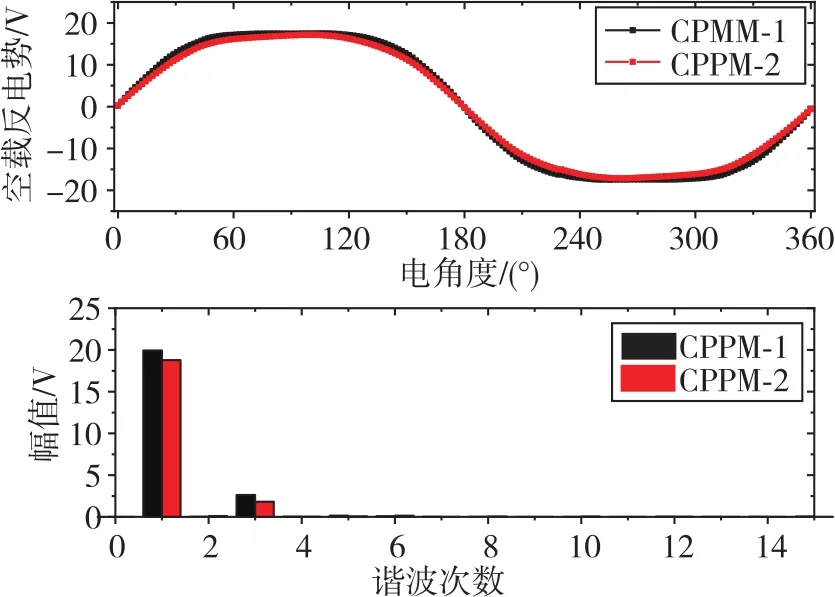
图21 CPPM-1电机与CPPM-2电机空载反电势波形及FFT分析对比Fig.21 Analysis and comparison of the back-EMF waveform and FFT between CPPM-1 motor and CPPM-2 motor at open circuit condition

为了验证定子齿不等宽对电机转矩脉动的优化效果，图16和图17分别给出了CPPM-2电机的齿槽转矩和转矩波形（红色曲线）。可以看出，CPPM-2电机的齿槽转矩峰峰值为17.4m·Nm。经计算，CPPM-2电机的平均转矩和转矩脉动为2.01N·m、2.76%。相较于CPPM-1电机，CPPM-2电机在平均转矩仅下降5.2%的情况下，转矩脉动减少了30.5%，优化效果较为明显。

5 结论

本文首先对CPPM电机转矩脉动的产生机理进行分析，总结出能有效削弱转矩脉动的方法，并利用有限元仿真软件对采用不同优化方法的CPPM电机进行仿真分析。仿真结果表明，通过采用优化永磁体极弧系数、永磁体不等极弧配合与定子齿偏心结构的方法，能够有效削弱CPPM电机的转矩脉动。本文为CPPM电机的转矩脉动抑制提供了一定的理论基础和技术借鉴，为CPPM电机在伺服系统中的推广应用提供了一定的参考。