现代电机优化方法综述

2022-01-19顾佳磊

导航与控制 2021年5期

花为，顾佳磊

（东南大学电气工程学院，南京 210096）

0 引言

电机优化设计在近年来得到了越来越多的关注。传统的电机优化主要通过参数扫描的方法进行，即对有限数量的优化变量通过离散步长进行网格分析，人为挑选出最为合适的候选设计。但是该方法效率低下，同时也难以获得全局最优解。对于多目标电机优化设计来说，传统的参数扫描方法可行性被进一步降低。

随着优化算法和建模技术的发展，电机优化设计得以与智能算法结合，出现了如遗传算法（Genetic Algorithm，GA）等智能算法指导下的电机优化思路。对于单一设计目标，电机设计已经能够实现其全局最优性能。而电机设计者追求的多个优化目标，如降低成本、减少损耗、提高效率等也通过智能算法的多目标版本得以实现。

智能算法指导下的大规模电机优化的主要缺陷在于大量的有限元分析（Finite Element Analysis，FEA）带来的庞大计算负担。一方面，可以通过减少使用甚至不使用FEA获取电机电磁性能，由此出现了代理模型法（Surrogate Models）、高效计算有限元法（Computationally-efficient FEA， CE-FEA）、磁网络法（Reluctance Networks Method， RNM）等方法。另一方面，从整体优化思路本身出发，尽可能提高优化过程的效率，由此产生了并行处理策略、子空间法以及基于敏感性分析的序列优化法等优化策略。

转速和功率密度的提升提高了电机的性能指标，实现了更高的效率和功率以及更低的成本和损耗，同时也使得电机处于设计极限处，此时必需考虑运行的最高温度、运动部件的受力情况、转子的临界转速等多物理场特性。再者，这些特性还会对电机电磁性能产生影响，电机设计者需要考虑到多场之间的相互耦合作用，电机设计已经从基本的电磁设计扩展到热、应力、结构、振动等多物理场综合分析。

电机应用场合日益丰富，牵引机等无固定工作点的电机已经不能通过只优化额定点来得到最优的电机设计。这类优化问题需要结合驾驶周期，选择工作周期内具有代表性的工作点，以期望提升整个驾驶周期内的电机效率。

确定性设计（Deterministic Approach， DA）无法考虑电机制造运行中不可避免的不确定性因素，电机鲁棒性优化方法（Robust Approach，RA）深入研究了不确定因素对批量产品性能的影响，相关研究主要围绕着电机鲁棒性分析和降低鲁棒优化计算资源两方面展开。

本文旨在呈现全面的电机优化设计综述：第一部分介绍了常用的多目标电机优化模型和智能优化算法；第二部分总结了减少优化时长的方法策略；第三部分归纳了当前电机优化的研究重点，包括驾驶周期优化、多物理场优化和鲁棒性优化；第四部分讨论了目前电机优化尚未解决的关键问题和未来的发展方向；最后进行了全文总结。

1 优化模型与优化算法

电机优化的主要目的在于确定与材料、拓扑和结构参数相关的一组优化变量，以满足如输出功率、效率、体积和成本等特定的设计指标和约束条件[1]。电机优化主要包括两个方面：确定优化模型和选择合适的优化算法。电机优化通常是多约束条件下的多目标优化问题，其一般表达形式为

式（1）中，p、m和D分别为优化目标f、约束条件g和优化变量x的数目，xu和xl分别为决策向量的上下取值边界。

权重组合法和帕累托最优解集法（Pareto Set）是处理多目标优化问题的两种常用方法。权重组合法通过赋予每个优化目标相应的权重，从而将多目标优化问题转化成单目标优化问题

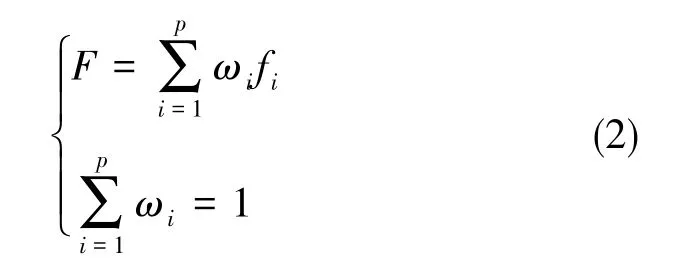
式（2）中，fi和ωi分别为第i个优化目标及其对应的权重。

权重组合法原理简单并且方便实施，但是权重的分配完全依赖于电机设计者对于不同优化目标重要性的经验判断，不同的权重分配情况将带来不同的最优结果。因此，如何科学地选择合适的权重系数是该方法难以解决的问题。

与常规单目标优化的显著区别是，多目标优化中每个优化目标之间存在着相互制约的矛盾关系，难以同时取得最优设计，也即某一个优化目标的改善将导致其他优化目标的恶化，从而使得最优结果不再是某个特定设计，而是存在多个全局最优解，它们共同构成了Pareto Set，这种方法被称为最优解集法，是拓宽折衷设计的最优选择[2]。如图1所示，红色圆点表示的最优解集是由一条曲线或者一个曲面构成的[1]。可以看出，不存在单个设计使得f1和f2同时取得最小值。 Pareto Set法的优点在于：获得最优解集之后，电机优化人员进而可以根据设计要求选择最为合适的设计结果。

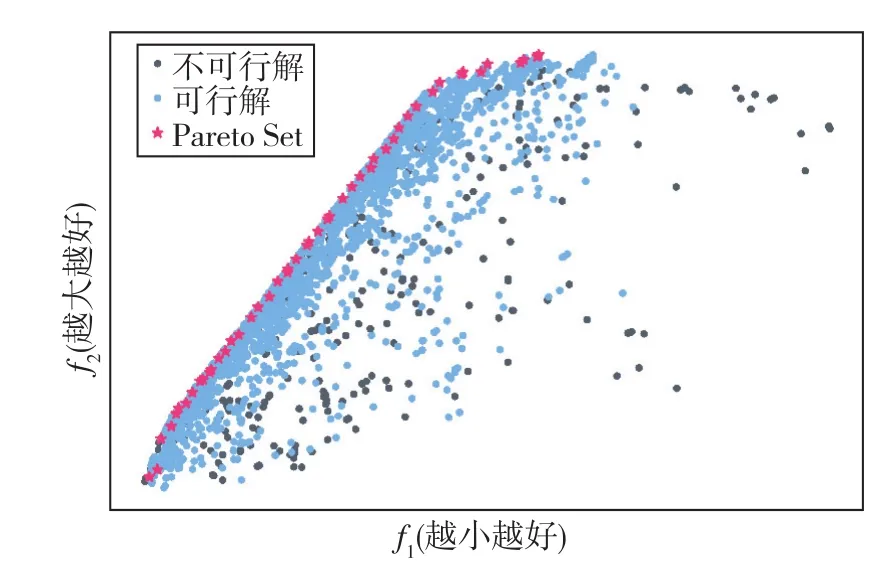
图1 以帕累托最优解集表示的优化结果Fig.1 Optimization results expressed in Pareto Sets

随着计算机软硬件技术的发展，人工智能（Artificial Intelligence，AI）技术在电机优化设计过程中得以应用，遗传算法、差分进化（Differential Evolution，DE）算法、粒子群优化（Particle Swarm Optimization，PSO）算法、蚁群优化（Ant Colony Optimization，ACO）算法以及其他智能算法促进了电机优化技术的快速发展。

文献[3]为了最大化平均转矩和最小化转矩波动，应用了改进PSO法对一台120W无刷直流电机（Brushless DC motor， BLDC）的永磁体长度、气隙长度和定子槽口宽度进行优化，并且将最优结果和GA的优化结果进行比较，证明了改进PSO法的结果质量、准确性、约束条件的处理能力以及计算效率都要优于GA。但是，PSO法存在着局部搜索能力差的缺陷，容易陷入局部最优。文献[4]指出DE的缺陷在于它需要额外的机制来处理带约束条件的优化问题，进而应用提出的结合差分进化的多目标优化算法（Combined Multiobjective Optimization with Differential Evolution，CMOD）对三台内置V型永磁同步电机（Permanent Magnet Synchronous Motor，PMSM）的成本和损耗进行优化设计，与DE优化结果的比较证明了CMOD的收敛速度、结果多样性、约束处理能力以及Pareto Set质量更为优越。文献[5]综述了PMSM驱动中最先进的控制和优化方法，总结了AI技术在电机控制中的研究进展，归纳的AI技术特征对电机本体设计具有很大的借鉴意义。

将各种改进的多目标算法版本计算在内，可以应用在电机优化中的算法种类庞大，这些算法各有优劣。在众多优化算法中，非支配排序遗传算法Ⅱ[6]（Non-dominated Sorting GAⅡ，NSGAⅡ）和Pareto强度进化算法Ⅱ[7]（Strength Pareto Evolutionary AlgorithmⅡ，SPEAⅡ）是应用最为广泛的优化算法，是处理多目标电机优化问题较为稳妥的选择。对于电机设计者而言，只需要选择合适且有效的优化算法，而无需追求所谓的最优算法。电机优化设计的难点和关键之处是如何将优化算法与电机优化过程有效结合，即采取何种优化策略以大大提高优化效率。

2 优化策略

在基于AI的大规模电机优化中，FEA法用来为每个候选设计计算适应度函数。FEA法可以获得高精度的电机性能，但是耗时严重，而智能优化算法通常需要评估成千上万的候选设计。以一个5维优化问题为例，则至少需要对5000（10×5×100）个候选设计计算性能指标，这对于大多数设计者来说是庞大的计算负担，学者们对此开展了相关研究并且提出了一些有效减小计算负担的优化策略。

2.1 代理模型

代理模型是一种代替大部分FEA的间接优化方法，和全FEA优化相比，代理模型可以显著减少计算耗时。值得注意的是，足够的预测精度是代理模型得以实施的前提，否则将导致不可靠的结果，这将毫无意义。换言之，代理模型的关键在于建立精度高而耗时少的方案，响应面法（Response Surface Method，RSM）、径向基函数法（Radial Basis Functions Model， RBF）、克里金模型（Kriging Model）和人工神经网络（Artificial Neural Network，ANN）模型是四种常用的电机优化代理模型。

除了在评估性能指标时可以借助于代理模型，在通过敏感性分析选择优化变量时也可以以采样获得的数据建立代理模型，在代理模型的基础上进行敏感性分析，从而提高计算效率。

RSM法利用光滑曲面拟合多维空间函数，可以使用自变量的线性项、二次项或交叉项作为基底，生成回归函数以逼近实际值。文献[8]对一台Halbach永磁电机的永磁体参数、定子参数、气隙长度等八个预选变量进行了敏感性分析，结果如图2、图3所示。

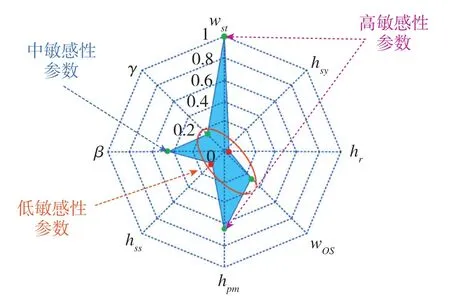
图2 气隙磁密THD敏感性分析结果Fig.2 Analysis results of air gap magnetic density THD sensitivity

图3 输出转矩敏感性分析结果Fig.3 Analysis results of output torque sensitivity

接着选择最小化气隙磁密谐波含量和最大化输出转矩作为优化目标，以对优化目标贡献最大的定子齿宽wst和永磁体宽度hpm建立RSM模型

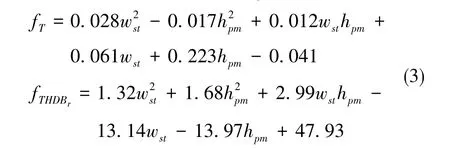
随后，采用杜鹃搜索算法获取Pareto前沿并且选择了近似的最优结果。这种在敏感性分析和性能函数计算阶段借助于RSM法的电机优化思路将复杂的电机问题转化成二阶数学方程寻优问题，简化了计算。但是只选择了两个变量构建RSM模型，也存在着预测精度较低的缺陷。

Kriging模型响应的计算公式为

式（4）中，X 为输入向量， f（X）为近似模型， β为待计算的参数向量，z（X）为随机误差。

预测结果包括确定项 fT（X）β和随机误差项z（X）两部分，样本之间的协方差为

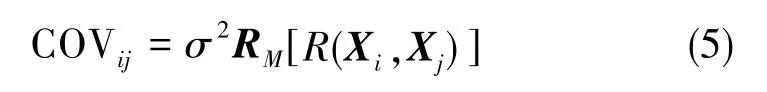
式（5）中，R为空间相关函数，由于Gauss模型能够提供一个相对平滑且可微分的表面，因而被广泛用作空间相关函数；RM为相关系数矩阵，由空间相关函数R构成

根据最佳线性无偏估计理论，预测结果和参数计算方法为[9]

式（7）、式（8）中， F、 r（X）和 Y 分别定义为

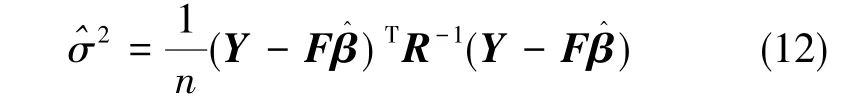
文献[10]应用Kriging模型对一台表贴式PMSM的转矩波动和损耗进行了优化，采取了权重组合法同时优化转矩波动和损耗两项电机性能。由于权重的选择依赖于设计者的经验，尽管提高了电机性能，但未能获得全局最优设计。

ANN模型模仿动物神经网络行为特征，根据相应的学习算法，能够对任意的非线性问题进行模拟。如图4所示，ANN模型主要由输入层、隐藏层和输出层三部分构成。输入层接收数据集信息并且传递给相邻的隐藏层，隐藏层通过转移函数处理数据，并将结果传递给下一隐藏层，直至输出层。在对电机性能做回归预测时，输出层将对传入的数据直接求和。

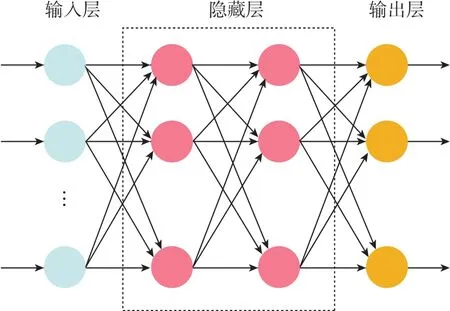
图4 人工神经网络模型基本结构Fig.4 Basic structure of ANN

文献[11]采用的单隐层BP神经网络对直线管状电机推力和推力波动进行建模学习，并且在验证集上分别取得了0.4%和1%平均预测误差的良好效果，随后该代理模型被用作电机温升情况研究。可见，合适的ANN模型经过训练能够高精度预测电机的性能，从而代替大量的FEA计算，减轻了电机优化计算负担。

RBF模型的基本思想是：组合多个径向基函数逼近某一给定函数。文献[12]对同步磁阻电机和内置永磁电机（Interior Permanent Magnet Machine，IPM）建立了RBF代理模型，得到了电流和磁链之间的关系，并且该代理模型包含了电机非线性特征和交叉耦合效应，从而获得了平滑且准确的d-q磁链波形，为涉及到磁链微分／积分计算的控制算法提供了极大便利。

2.2 CE-FEA

文献[13]～文献[15]介绍了高效计算有限元法CE-FEA，该方法充分探索了电路和磁路的对称性，减少了计算所需的静磁有限元数目。CE-FEA能够用最少的静磁解得出反电势、平均转矩、齿槽转矩、转矩波动以及铁心损耗等电机性能参数，相比时步有限元法，保留了有限元法的高精度和能够考虑饱和的优点，同时大大减少了计算时间。

文献[15]详细介绍了CE-FEA在PMSM建模和参数设计中的作用，给出了主要电磁性能的计算方法：对于三相PMSM来说，一个完整电周期的磁链可以由1／6电周期内的三相磁链拼接而成；接着对拼接后的磁链进行快速Fourier分解，可以得到磁链的Fourier级数形式

式（13）中，λa为A相磁链的瞬时值， λv和ϕv分别为磁链的v次谐波幅值和对应的相位，θ为电角度位置，vM为截断的最高次级数次数。

将磁链关于时间进行微分，可以得到反电势的表达式为

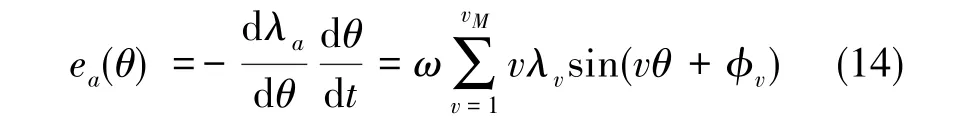
式（14）中，ω 为同步频率，单位为 rad／s。

电磁转矩根据虚功法进行计算

式（15）中，P为极数，Wstore为磁路中储存的能量，θm为机械角度位置，ia、ib和ic分别为A、B、C三相电流的瞬时值。

文献[14]指出，在CE-FEA计算电磁转矩时，为了计及12次转矩谐波，需要至少5个静磁有限元结果，该方法非常适合应用到大规模电机设计优化的研究之中。

径向和切向磁密的表达式如下

式（16）中， Br，t为定子铁心内径向或切向磁密，k为正整数，θs为电角度表示的槽距，r为电机径向位置，t为铁心磁密瞬时值对应的时刻。

磁密的Fourier级数形式为

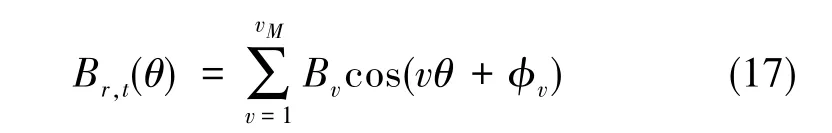
式（17）中，Bv为v次磁密幅值。

CE-FEA法计算定子铁损时，只计算磁滞损耗和涡流损耗。根据损耗模型，单位质量下的损耗表达式为

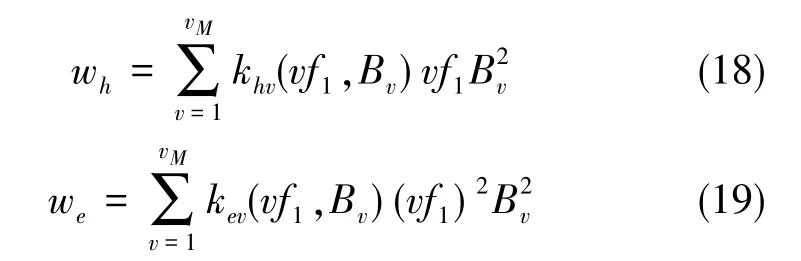
式（18）、式（19）中， wh和 we分别为单位质量的磁滞损耗分量和涡流损耗分量，khv和kev分别为对应的损耗系数，vf1为谐波频率。khv和kev都是频率和磁密幅值的函数，可以用磁密幅值的三次多项式表示[16]。

文献[17]结合CE-FEA法和解析法对永磁体涡流损耗进行了研究，其基本思想为：把永磁体进行分层分段，假定每个单元内的磁密一致，通过磁密计算反电势，结合等效电阻进行积分求取永磁体涡流损耗，并和2D、3D有限元结果进行了比较，验证了方法的正确性。其中，磁密波形经由转子侧的时空转化法[13]进行重组，即由最小周期单元内不同位置的磁密拼接而成。

2.3 磁网络模型

磁网络法通过把电机磁路与电路类比，以平衡计算时间和计算精度。文献[18]按照不同转子位置下的气隙磁路对磁通切换电机进行磁路划分，建立等效磁网络模型，通过迭代求解，计算了电机的静态特性，但是这一方法依赖于具体的电机结构，通用性不足。当电机结构发生较大变化时，需要对磁网络模型进行修改，而且气隙磁路与位置有关，需要多个磁网络模型。针对该方法的缺陷，文献[19]、文献[20]提出了基于网格划分的磁网络法（Mesh-based Generated Reluctance Networks Modelling，MBGRN）。文献[21]给出了负载下MBGRN的建模方法，并且考虑了磁路饱和，给出了磁链、反电势、推力、铁心损耗的计算方法，通过与有限元结果的比较验证了MBGRN法的有效性。

然而，这种划分方式在气隙部分产生了大量的磁阻单元，增加了计算负担，削弱了磁网络法计算成本低于有限元法的优势。

MBGRN法在处理气隙时存在的上述问题催生了一种将网格划分与解析法相结合的建模方法：混合解析模型（Hybrid Analytical Modeling， HAM）。以表贴式PMSM为例，该方法的基本思想为：将定子通过MBGRN建模，其他部分（气隙和转子）建立解析模型，通过使交界面的标量磁势相等并计算分界面节点处从气隙侧传入的磁通完成模型之间的耦合，如图5[22]和图6[19]所示。

图5 混合解析模型法示意图Fig.5 Schematic diagram of HAM

图6 HAM耦合示意图Fig.6 Schematic diagram of direct coupling of HAM

文献[22]～文献[25]依据HAM法对电机进行建模分析。文献[22]对一台混合励磁同步电机的原始结构和忽略转子槽之后的结构分别建立了解析模型，并与定子磁网络模型耦合，比较了两种模型下的电磁性能，发现尽管第二种模型忽略了转子槽结构，其结果仍然保持了相对好的准确性。文献[23]开展了永磁直线电机的相关研究，验证了HAM模型相比有限元法良好的准确性，并且极大地减少了计算时间。文献[24]、文献[25]分别基于HAM模型研究了直线管状磁通切换电机和直线永磁电机的齿槽力，取得了很好的效果。

文献[26]将MBGRN和HAM两种磁网络建模方法进行了比较分析，得出了两种方法都能准确计算电磁性能并且相比之下HAM法更为优越的结论。由此可见，结合磁网络模型和解析计算的HAM法，既保持了MBGRN磁网络拓扑通用性强的优点，又有效降低了计算负担，有助于提升电机优化效率。

2.4 其他方法

文献[27]从侧重于计算时间的角度对电机优化方法进行了总体介绍，并且比较总结了不同方法之间的差别，如表1所示。

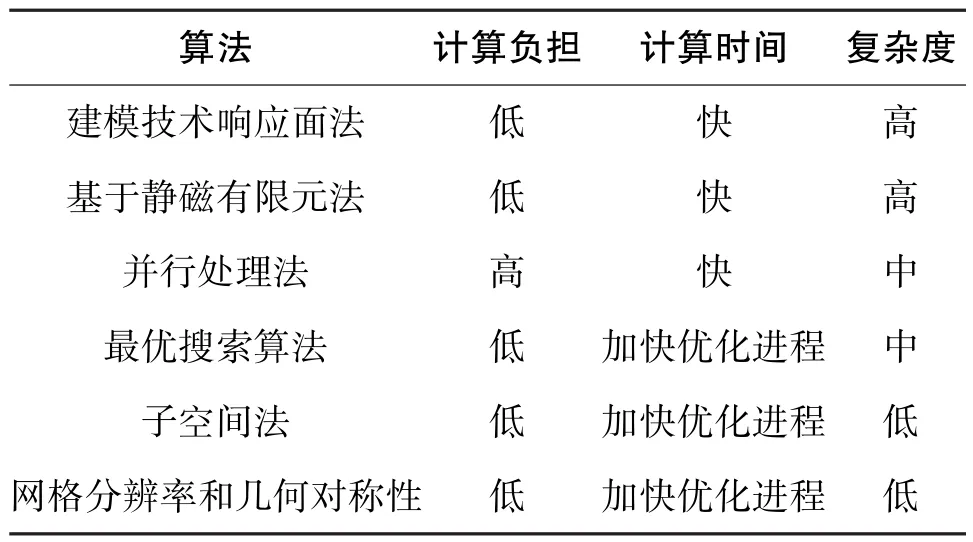
表1 优化方法比较Table 1 Comparison of optimization methods

除了代理模型、CE-FEA、磁网络法外，还有并行处理法[28-29]、子空间法[30-31]等其他降低计算时间的方法。并行处理仍然基于有限元仿真，依靠计算机群同时计算以加快优化进程。子空间法考虑到多个目标函数可以对应不同分布、不同数目的采样点，通过在不同子区域选取数目不同的采样点以有效减少计算时间。合理地运用或者组合这些方法，都能够显著降低电机优化的整体耗时。

3 研究重点

3.1 驾驶周期优化

常规电机优化设计局限在额定工作点处，如今已有学者结合实际应用，将电机优化拓展到多工作点上。文献[32]以一台具有较宽恒功率区间的IPM为研究对象，对额定工作点和最大转速工作点进行了优化，以提高这两个工作点的输出转矩，降低电机质量，同时提高最大转速。如式（20）所示，以惩罚函数的形式在目标函数中引入了约束条件的影响。

式（20）中，gm为第m个约束条件，ε为惩罚参数。

如电动汽车牵引用等没有明确工作点的电机，其工作区域非常广泛，对这类电机的优化研究需要依据驾驶周期进行，公路燃油经济性测试驾驶时间表（Highway Fuel Economy Test Driving Schedule， HWFET）、城市驾驶时间表（Urban Dynamometer Driving Schedule，UDDS）和新欧洲驾驶曲线（New European Drive Cycle， NEDC）是相关研究中比较常见的驾驶周期。

结合美国驾驶时间表，文献[33]优化了二代Prius IPM的材料成本和功率损耗，给出了基于驾驶周期的电机优化基本流程。依据能量分布，采用k-均值聚类法选择代表工作点，每一个代表点附近的工作点数则反映了该代表点对应的权重。

也有文献从能量的角度选择代表工作点。文献[2]结合NEDC采取不同于聚类的策略选择代表点，将能量最高的6个工作点予以保留，随后把转矩转速平面人为分成6个子区域，每个子区域根据其中工作点的能量和转速计算出代表点，由此而新产生的6个代表点不一定是电机工作中的实际运行点。文献[34]把NEDC按照时间分区，将每个区域内功率看作是时间的常量或者线性函数，通过式（21）以功率对时间的积分给出了单位时间步长内能量的计算方法，而后结合差分进化算法对内置式和表面式永磁电机进行了优化。

式（21）中，ai为第i个时间区间内线性功率方程的斜率，E0为初始能量。

文献[35]采用一种基于自适应网络的模糊推理系统（Adaptive Network-based Fuzzy Inference System，ANFIS）训练了计算效率云图的代理模型，实现了整个驾驶周期内能量的计算，并且通过计算Euclidean距离结合进化算法，找到了电机工作的标称点，从而舍弃了工作点能量计算和聚类的工作。这种代理模型能够快速计算出能量，但是在每一代种群里，都需要对网络重新训练，这就加大了时间负担。还有的相关研究拓宽了所研究的电机类型和应用场合，文献[36]的研究对象是电动方程式赛车用轮辐式永磁电机；而文献[37]研究的则是五相磁通切换永磁电机，在驾驶周期优化的目标下，采用CE-FEA获取电磁性能，同时通过MATLAB完成与ANSYS／Maxwell的数据交换和数据处理，给出了自动化优化实现的方法。这种如图7所示的自动化优化方法已经能够将智能算法和优化策略应用到电机优化之中，为今后更为复杂、功能更为全面的电机优化平台提供了实现思路。

图7 MATLAB与ANSYS／Maxwell仿真之间的数据交换Fig.7 Data exchange between MATLAB and ANSYS／Maxwell simulation

3.2 多物理场优化

传统的电机设计偏重于对电机电磁部分进行研究，但是电磁性能会受到电机结构、温度的影响，单纯进行电磁优化难以满足设计要求。基于多物理场的电机优化研究关键在于解决两点问题：

1）如何考虑多场之间的关系；

2）采取何种多场计算方法。

对于第一点，首先考虑电磁场和温度场之间的关系。一方面，电机温度分布会影响材料属性，进而影响电磁性能；另一方面，电磁性能变化导致损耗改变，进而又会影响电机温升。文献[38]、文献[39]对磁热双向耦合计算开展了研究，结合有限元电磁计算与热网络温升计算实现双向耦合，提高了计算精度。其次，考虑了温度与应力之间的关系，温度会影响护套与转子部件之间的接触情况。文献[40]推导了表面式PMSM在不同材料护套下永磁体转子强度的解析解，研究了转速和温度等因素对转子强度的影响。

对于第二点，一方面，由于多物理场分析的复杂性，相关研究多着重于多场特性的分析和验证。多场设计流程由若干步骤顺序进行，任何一步结果不满足要求都会返回上级而产生新的迭代循环[41]。另一方面，为了保证精确的计算结果，多物理场特性依赖于有限元或者流体计算[42]，耗时严重，限制了多物理场优化在电机优化中的发展。

针对上述多物理场优化中存在的问题，文献[43]、文献[44]借助于 ANSYS／Workbench搭建了优化平台，电磁计算采用有限元法，温度计算采用热网络模型，应力采用解析法以缩短优化时间。文献[45]基于有限元样本数据建立了磁链模型、铁损模型和永磁体损耗模型用于计算电磁性能，基于转子结构建立解析转子机械应力模型用于计算给定位置的最大应力，建立集中参数热网络用于预测电机温升。该方法能有效减少计算时间，并且能对多个工作点进行分析。文献[46]更进一步，建立了电机性能的Kriging代理模型，结合遗传算法完成了对高速电机转子部分的优化设计。

值得注意的是，当面临复杂的设计要求时（比如多物理场设计），如图7所示的简单自动化电磁优化框架已经不能满足设计需要。如果借助于ANSYS／Workbench，又无法将先进的优化策略应用其中。总之，目前尚未有成熟且功能强大的电机自动化优化平台，这是未来电机优化发展有待解决的问题。

3.3 鲁棒性优化

为了充分利用材料，获取最佳电机性能，优化设计的最优结果通常将电机设计在约束极限附近。这种确定性设计方法没有考虑到如材料分散性、加工公差等不可避免的不确定性对批量产品性能的影响[47-48]，从而无法保证大批量产品保持可靠的高性能。从图8可以看出，确定性最优设计对不确定性参数非常敏感，容易超出可行域造成产品失效，由此催生的电机鲁棒性最优设计能够在不确定性参数影响下将电机性能保持在约束范围之内[48]。

图8 确定性设计和鲁棒性设计的示意与比较Fig.8 Illustration and comparison of deterministic and robust designs

从质量管理技术中产生的六西格玛设计方法（Design for Six-sigma，DFSS）作为一种鲁棒设计方法，被采用解决上述DA方法的缺陷。文献[48]、文献[49]分别将DFSS应用到单目标和多目标电机优化中，针对鲁棒设计庞大计算成本的特点，提出了一些降低计算负担的策略。

DA优化模型（式（1））通过DFSS方法处理得到的鲁棒优化模型为

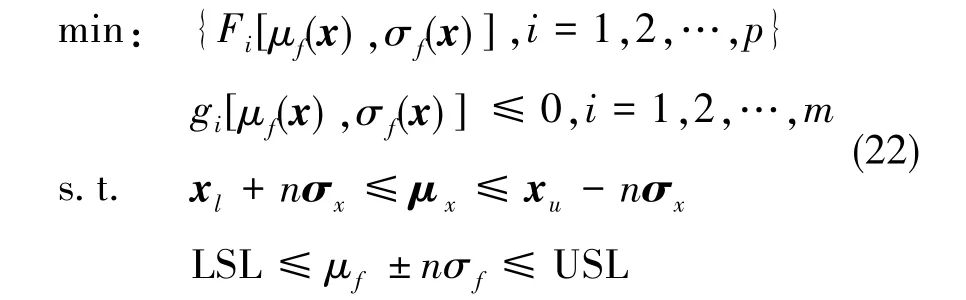
式（22）中，μ和σ分别为均值和标准差，并且通常由蒙特卡洛分析法（Monte Carlo Analysis，MCA）计算；LSL和USL分别为下边界和上边界，n为西格玛水准，在DFSS设计中通常取为6。

DFSS设计通过求解性能函数的均值和方差实现了电机鲁棒优化设计，但是采用MCA法计算均值和方差又显著增加了计算负担。文献[50]分析了随机不确定性变量和区间不确定性变量对鲁棒设计的影响，提出了多项式潮流切比雪夫区间法（Polynomial Chaos Chebyshev Interval， PCCI）展开不确定性区间内的电机性能函数，并且通过区间算数估计均值和方差的边界，有效减少了鲁棒优化的计算负担。当电机设计者希望保持大批量产品性能可靠性时，鲁棒性优化是减少次品率的有效手段，也是今后电机优化发展的重点之一。

4 展望

各种优化策略和研究重点都是辅助电机设计者优化电机的有效工具，对于电机设计者来说，合理的电机优化步骤应如图9所示。首先应该将电机工况、物理场特性、产品数量、优化层级与电机应用场景和设计要求进行比对，从而选择相应的优化方法，并在此基础上得到满足要求的初始设计，进而根据电机类型和电机拓扑建立优化模型，选择合适的智能算法和优化策略，完成最优设计。

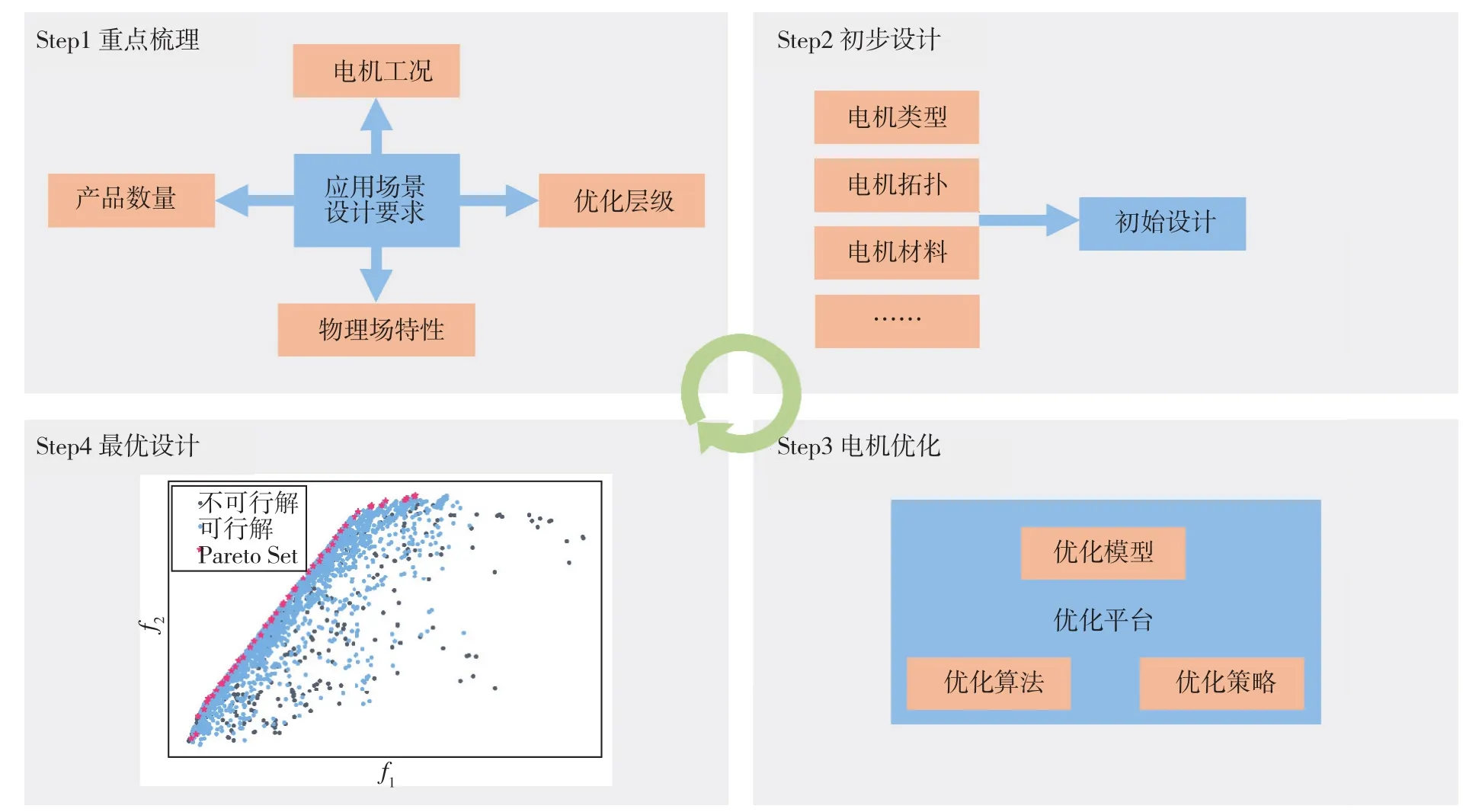
图9 电机优化流程Fig.9 Diagram of electrical machine optimization process

尽管目前的优化技术已经显著提高了电机优化效率，但是仍然存在着一些问题尚未完全解决。首先是对电机设计中不确定性的研究还不够充分，采用式（22）进行鲁棒性优化，特别是面对不确定种类多样的情况下，通过目标函数和约束条件的均值和方差上界表征不确定性对性能函数的影响，存在着区间缩放导致的先天性误差，如何获取确切的参数取值目前尚未有相关研究。同时，电机性能无可避免涉及到FEA计算，而鲁棒性优化对每个候选设计都需要额外的计算量以评估其鲁棒性，这极大地加剧了优化的时间成本。尽管此时可以借助于代理模型降低计算负担，但是在候选设计附近小区间内的性能预测给代理模型的精度带来了巨大考验，权衡好鲁棒性和电机性能之间的相对关系也是电机鲁棒优化值得研究的地方。

其次，系统级的电机优化（System-level）也是未来的研究重点。目前，电机优化大多聚焦于电机本体设计，鲜有将电机本体和控制系统结合、统一优化的方案。为了得到驱动系统的最优动态特性，系统级优化不仅优化电机的拓扑结构，还对PI参数等控制部分的变量进行优化。此时，优化变量维度的增加导致电机优化问题变得更为复杂，有学者将分层优化策略应用到系统级优化中，缓解了这一问题，将变量根据敏感性分成若干层次，按照从高到低的顺序依次优化[9，51]，也有学者将系统级优化应用到基于驾驶周期的电机优化中[52]。可见，系统级优化和其他研究重点的结合也是之后电机优化的研究关键之处，有助于从整体上获取最优电机设计。但是，与之而来的是更为复杂、更为难以处理的优化问题，设计者应该结合优化策略研究出相应的有效方法。

最后，一个无法避免的问题在于电机优化的计算负担。智能算法需要评估成千上万的候选设计，而电机性能主要通过FEA计算得到，如此多次的有限元调用对于绝大多数设计者来说都是难以完成的。因此，在优化模型中采用高效的优化策略是必不可少的。但是，脱离了FEA，计算精度必然会下降。同时，预测精度再高的代理模型也无可避免会出现极个别预测偏差过大的情况。如何正确权衡计算时间和计算精度之间的关系，改进现有的或者提出新的优化策略，是电机优化方法发展的关键方向。