非对称转子永磁辅助式同步磁阻电机优化设计

李 敏，赵文良，杨智铄，刘 炎

（1.山东大学电气工程学院，济南 250061；2.中国航发控制系统研究所，无锡 214063）

0 引言

永磁电机被广泛应用于工业、交通运输以及航天航空等领域，然而随着近年来稀土材料价格的上涨和材料供应的紧张，这些领域面临严峻的挑战[1-3]。因此，研究使用少量或者无稀土材料的高性能电机成为现阶段研究的热点。在电机研究及发展过程中，凸极同步电机双反应理论的提出使得具有凸极效应电机中的磁阻转矩得到了更好的分析与应用，推动了凸极电机的发展和研究。同步磁阻电机依靠磁阻最小原理获得磁拉力，不需要稀土永磁材料，仅通过d轴、q轴磁阻差值来获得转矩，从而降低了电机对稀土材料的依赖。但同步磁阻电机相较于稀土永磁电机，普遍存在效率及功率因数较低的问题，当需要获得足够大的输出转矩时，电机通常体积较大且定子侧需要提供较大的电流。

为提升同步磁阻电机的电磁性能，在其转子磁障中添加适量永磁体从而增加d轴方向磁通，即提出永磁辅助式同步磁阻电机（PMA-SynRM）[4]，该种电机相较于同步磁阻电机，转矩密度和功率因数均显著提升。PMA-SynRM对永磁体性能要求不高，电机制造成本较低，与永磁电机相比具有更宽的调速范围，其设计及应用成为了当今研究的热门课题。传统PMA-SynRM具有永磁转矩和磁阻转矩两种转矩成分，但各转矩成分不能充分利用。基于此，文献[5]提出了一种非对称转子结构的电机模型来改变永磁转矩和磁阻转矩的叠加耦合关系，从而提高PMA-SynRM各转矩成分的利用率，实现输出电磁转矩的提高。文献[6]研究了一种轴向组合转子的电机拓扑结构，通过改变磁阻转子和表贴式转子的安装角度从而实现永磁转矩最大值和磁阻转矩最大值在相同电流相位角处叠加，提高两种转矩成分的利用率以提升转矩。文献[7]设计了一种双转子结构的电机，同样通过改变内外转子的安装角度来提高电机对永磁转矩和磁阻转矩的利用率。上述研究所提出的电机模型虽然可显著提升电磁转矩，但同时带来高转矩脉动的问题。

PMA-SynRM的高转矩脉动严重影响到电机转矩输出的质量[8]。文献[9]对比总结了不同功率下同步磁阻电机、内置式永磁电机和PMA-SynRM的转矩脉动情况，表明了降低PMA-SynRM的转矩脉动在电机设计优化过程中是一个不可忽视的问题。抑制转矩脉动常见的方法一般分为两大类，一类是通过优化驱动控制算法从而实现抑制转矩脉动的目的[10]；另一类是在电机本体上进行拓扑结构设计实现抑制转矩脉动的目标，主要方法有：极槽配合与绕组分布法[11]、极宽调制法[12]、斜极法[13]、优化极弧系数[14]、不等槽口宽配合[15]、正弦波磁极[16]和开辅助槽[17]。对于特殊转子结构的PMA-SynRM，通过在转子侧设计抑制转矩脉动的方法可能会影响电机本身的电磁性能，甚至会破坏其输出转矩特性，所以齿槽转矩和转矩脉动优化可选择在定子侧或驱动方法上进行研究。

本文在前期工作[5]提出的非对称转子结构PMA-SynRM的基础上，以削弱齿槽转矩和转矩脉动为目标，同时保证其聚磁效果和转矩叠加效果的稳定性，分别采用定子侧开辅助槽和改变极槽配合两种方法进行优化分析，并对不同定子槽数和绕组分布形式的定子磁动势进行分析比较，最后通过有限元方法对优化前后的电机模型电磁性能进行对比分析，验证优化设计方法的有效性。

1 电机基础拓扑结构

选取文献[5]提出的具有非对称转子结构的4极6槽PMA-SynRM作为基础电机模型，其定转子剖面示意图分别如图1（a）和图1（b）所示， 该非对称转子结构的特殊性体现在一个磁极内永磁体和磁障配置左右分布是不对称的。基础电机模型的定子绕组形式为集中绕组，转子中永磁体充磁方向如图1（b）中的虚线箭头所示，磁障中可选用塑料或树脂等非导磁材料填充以增加转子的结构强度。

图1 基础电机模型剖面图Fig.1 Topology of the basic motor model

传统PMA-SynRM中永磁转矩和磁阻转矩叠加关系如下

式（1）中，Tem为电机输出的电磁转矩，p为极对数，ψpm为永磁体在定子绕组中产生的基波磁链幅值，Ia为定子相电流幅值，β为定子相电流与q轴的夹角，Ld为d轴电感，Lq为q轴电感，Tpm为永磁转矩，Tre为磁阻转矩。

由式（1）可知，电机输出转矩由两部分组成，第一部分是与永磁体磁链有关的永磁转矩，第二部分是与电机的d轴、q轴电感有关的磁阻转矩。可以看出，永磁转矩周期是磁阻转矩周期的2倍，永磁转矩和磁阻转矩分别在不同的电流相位处取得最大值，所以传统PMA-SynRM不能充分利用其永磁转矩成分和磁阻转矩成分。由式（1）可得出永磁转矩、磁阻转矩和两者叠加而成的电磁转矩三者之间的关系，如图2所示，永磁转矩曲线和磁阻转矩曲线在不同电流相位角处达到最大值，二者相差45°（电角度）。本文研究的PMA-SynRM通过非对称转子设计改变磁路结构，将磁阻转矩最大值所对应的电流相位角进行偏移，使其与永磁转矩最大值所对应的电流相位角相同或者相近，转矩特性如图3所示。非对称转子PMA-SynRM作为研究的基础电机模型，其主要规格参数如表1所示。

图2 传统PMA-SynRM转矩特性图Fig.2 Torque characteristics of conventional PMA-SynRM

图3 基础电机模型转矩特性图Fig.3 Torque characteristics of basic motor model

表1 基础电机模型参数Table 1 Specifications of basic motor model

2 电机改进拓扑结构

分别采用定子侧开辅助槽和改变极槽配合的方法对基础电机模型进行优化设计以实现抑制齿槽转矩和转矩脉动的目标，在对电机基础模型进行优化的过程中，保持转子各参数以及定子内外径为定值。

开辅助槽是通过降低齿槽转矩来实现对电机转矩脉动的抑制。通过合理的辅助槽数目、宽度以及深度等参数的设置，能够显著抑制齿槽转矩，且开辅助槽前后空载反电动势变化较小，同时降低了气隙磁密波形畸变率，使齿槽转矩降低的同时改善了气隙磁密的波形。齿槽转矩定义为电机不通电时的磁场能量W对定转子相对位置角α的负倒数[18]，其表达式为

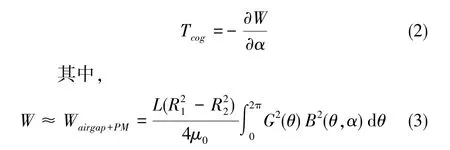
式（3）中，L为电机定子铁芯的轴向长度，R1为电机定子的外径，R2为电机定子的内径，μ0为空气磁导率， G（θ）为气隙的磁导函数， B（θ， α）为等效无槽电机气隙中的磁密分布函数。

在定子齿开辅助槽相当于增加定子槽数，即改变极槽配合数，常用于电机定子槽数和转子极数不能改变的情况下。因为电机转子非对称、结构复杂，对其进行解析计算过于复杂，所以辅助槽尺寸可根据经验通过试错法进行选取。定子齿开辅助槽的经验一般为：辅助槽要均匀分布于定子齿上，辅助槽位置应当关于两个定子槽中线对称。单一定子齿开辅助槽数k的选取应满足：当Np≠1时，k+1≠mNp。其中，m为任意自然数，Np为周期数，Np满足[18]

式（4）中，z为定子槽数，GCD为取最大公约数运算符。于是，单一定子齿上辅助槽数k=2。

辅助槽选择矩形槽，辅助槽的宽度W和深度d与槽口的宽度W0和深度d0一般满足式（5）时，能取得对齿槽转矩较好的削弱效果[19]。

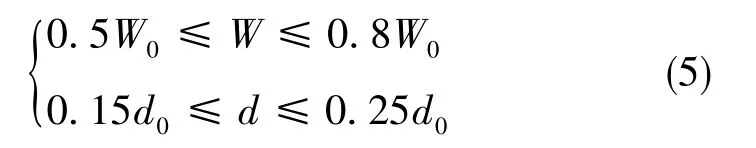
根据基础电机模型定子槽口的参数，定子侧辅助槽的宽度 W=1.5mm，辅助槽的深度 d=0.4mm，最终通过开辅助槽改进得到模型Ⅰ的定子，如图4所示。

通过改变极槽配合及绕组分布对转矩脉动进行抑制时，尽可能使周期数Np变大，齿槽转矩随着周期数的增大而减小。通过改变定子槽数，使式（4）中分母部分的值减小，能够有效增大周期数Np，从而降低齿槽转矩幅值，有利于转矩脉动的抑制，是降低齿槽转矩时最常采用的方法。采取分布式绕组来降低定子磁动势中谐波对转矩脉动的影响，结合电机制造中定子齿和定子轭的相关要求，改进的模型Ⅱ选取27槽平行齿定子，定子模型及绕组布线如图5所示。

图5 模型Ⅱ定子结构及绕组分布图Fig.5 Stator and winding distribution of modelⅡ

3 定子磁动势分析

转矩脉动主要是定子电流谐波磁动势与转子磁动势相互作用产生的谐波转矩，所以定子磁动势是影响转矩脉动的关键因素之一。对不同定子结构和不同绕线方式下的电机定子做磁动势分析有利于明确其对转矩脉动的影响。

基础模型和模型Ⅰ都采用的是6槽集中绕组，其磁动势波形如图6（a）所示；模型Ⅱ采用的是27槽分布式绕组，其磁动势波形如图6（b）所示。

图6 定子磁动势波形Fig.6 Diagram of stator magnetomotive force waveform

对6槽集中绕组的磁动势波形和27槽分布式绕组的磁动势波形分别作快速Fourier分析，得到的Fourier级数表达式分别为

式（6）、 式（7）中，N 为每相绕组匝数， i为每相电流的有效值。

因电机极对数为2，所以n=1时为次谐波磁动势，n=2时为基波磁动势，n为大于1的奇数时为分数次谐波磁动势[20]。由式（6）、式（7）得到的6槽集中绕组和27槽分布式绕组基波磁动势的幅值分别为0.827Ni和4.043Ni。以各自基波磁动势幅值为基值，对所有谐波的幅值进行标幺化，得到不同定子磁动势的谐波频谱图，如图7所示。由图7可知，27槽分布式绕组相对于6槽集中绕组而言，虽然产生了次谐波磁动势和分数次谐波磁动势，但是其各次谐波磁动势的相对幅值之和都明显小于6槽集中绕组产生的各谐波磁动势的相对幅值之和。

4 电机性能对比分析

采用有限元方法对电机模型进行建模与分析，仿真条件如下：1）所有电机模型定子的内外径保持不变，转子各结构参数保持不变，且使用相同的永磁材料和用量；2）电机输入恒定，其每相绕组匝数、额定电流相同。首先对三个电机模型的空载特性进行分析比较，图8为空载气隙径向磁通密度波形。可以看出，模型Ⅰ的气隙径向磁密波形与基础模型的气隙径向磁密波形相似，不同点在于因在定子槽口附近开了辅助槽，导致在定子槽口附近的径向磁密波形出现了凹陷。模型Ⅱ因改变了定子齿的形状以及定子槽的数量，气隙径向磁密的波形较基础模型有很大改变，幅值比基础模型增大了80%，该27槽定子结构更能凸显非对称转子结构的聚磁特点。图9（a）为三个电机模型的反电动势及其基波反电动势波形，基础模型、模型Ⅰ和模型Ⅱ的基波幅值分别为20.09V、19.81V和21.29V。对其反电动势进行快速Fourier变换分析，其结果如图9（b）所示，三个模型的总谐波畸变率分别为40.1%、37.8%和32.4%。模型Ⅱ与基础模型相比，基波反电动势增加了6%，总谐波畸变率降低了19.2%。空载情况下，模型Ⅱ在气隙径向磁通密度、反电动势和总谐波畸变率上都优于基础模型。图10为三个电机模型的齿槽转矩波形对比图，可以看出，模型I和模型II的齿槽转矩相对于基础模型的齿槽转矩分别降低了30%和94.5%。

图8 气隙径向磁密分布图Fig.8 Radial magnet density distribution of air gap

图9 反电动势及其Fourier分析Fig.9 Diagram of back electromotive force and its Fourier analysis

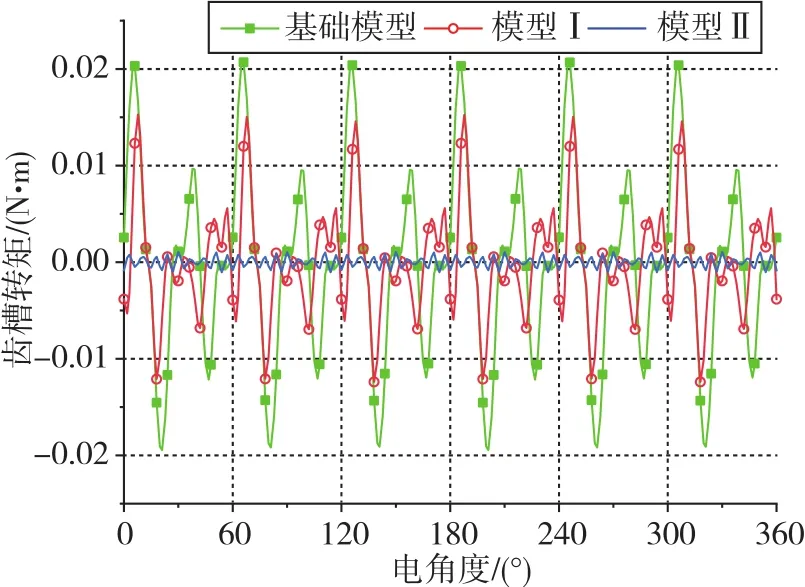
图10 齿槽转矩波形Fig.10 Diagram of cogging torque waveform

然后对两个改进后的电机模型在额定负载情况下的转矩特性进行分析，对两个改进的电机模型分别采用冻结磁导率法分析其转矩特性，研究不同电流相位角下永磁转矩和磁阻转矩的叠加耦合关系。冻结磁导率法分离转矩流程如图11所示，得到改进后电机模型的转矩特性曲线如图12所示。模型Ⅰ的永磁转矩、磁阻转矩和总电磁转矩的最大值分别在电流相位角为-5°、10°和5°处取得，模型Ⅱ的永磁转矩、磁阻转矩和总电磁转矩的最大值分别在电流相位角为-5°、5°和0°处取得。由此可见，改进后的模型I和模型II都没有改变该电机对转矩成分进行特殊耦合叠加的特点，依然保证了磁阻转矩和永磁转矩在相近的电流相位角处进行叠加，而且模型II的定子结构对于该非对称转子有更好的聚磁效果，更利于提升电机的电磁转矩。

图11 冻结磁导率法分离转矩流程图Fig.11 Flowchart of frozen permeability method for torque separation

图13为额定负载下三个电机模型的磁通密度云图。可以看出，模型Ⅰ与基础模型的磁通密度分布接近，而模型Ⅱ的定子轭磁通密度明显低于基础模型。这表明三个模型中定子轭在具有相同磁密饱和值的情况下，模型Ⅱ的绕组可以流过更大的电流且定子轭不容易发生饱和。

图13 磁通密度分布图Fig.13 Diagram of magnetic flux density distribution

图14为额定负载下电机电磁转矩输出最大时三个电机模型的电磁转矩波形。可以看出，基础模型、模型Ⅰ和模型Ⅱ的平均电磁转矩分别为0.284N·m、0.277N·m和0.291N·m。相对于基础模型，模型Ⅰ的转矩脉动没有变化，而模型Ⅱ的转矩脉动降低了87.83%。改进前后的电机性能分析结果如表2所示。

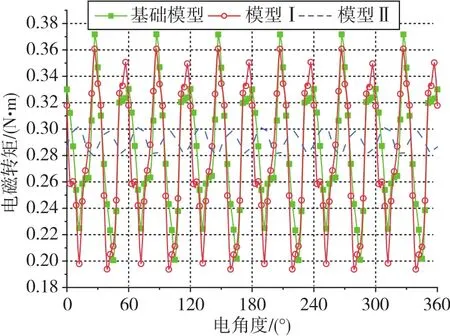
图14 电磁转矩对比Fig.14 Comparison of electromagnetic torques

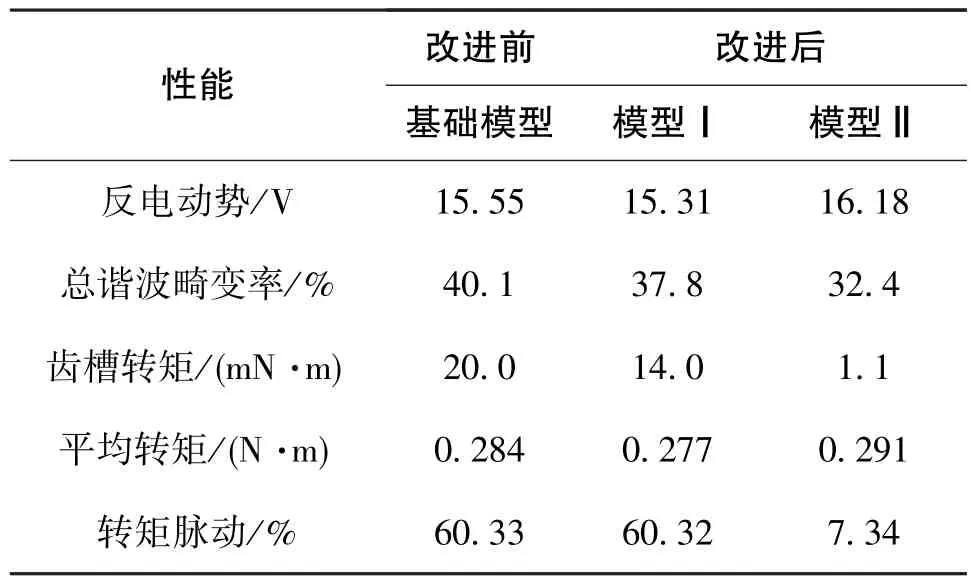
表2 电机性能分析结果Table 2 Analysis results of motor performance

5 结论

本文针对新型非对称转子PMA-SynRM齿槽转矩和转矩脉动过大的问题进行了优化设计研究，在保证该电机转矩特性不发生改变的情况下，分别通过定子开辅助槽和改变极槽配合及绕组分布形式两种方法对齿槽转矩和转矩脉动进行抑制。首先对不同极槽配合下的定子磁动势谐波进行了对比分析，然后通过有限元方法分析比较了改进后电机模型的电磁性能。结果表明，采用27槽分布式绕组定子结构对该非对称转子PMA-SynRM的齿槽转矩和转矩脉动有更好的抑制作用，并且可以提高反电动势的正弦性、降低总谐波畸变率和增强其非对称转子的聚磁特性，显著提升了电磁性能。本文为非对称转子PMA-SynRM的转矩脉动抑制提供了理论和技术参考，促进了该种电机的推广应用。