基于无差拍电流预测控制的六相PMSM容错控制

徐 磊，许 强

（华中科技大学，武汉 430074）

0 引言

近年来，大功率化和高可靠性化成为交流电机变频传动系统的主要发展方向之一，而其中较为热门的提高交流变频调速功率和可靠性的方案就是采用多相电机。与三相电机相比，多相电机具有如下优势[1-3]：1）转矩脉动幅值与电机相数成反比，电机振动和噪声减小；2）每相输出功率低，降低了对开关器件的要求，可以实现低压大功率；3）电机冗余性强，可以实现容错运行，适合在要求高可靠性的场合下应用；4）具有多个控制自由度，可以施加更多的高性能控制策略。基于多相电机具有以上优点，对多相电机的高性能控制策略进行研究具有很大的工程意义和价值。

多相电机的控制主要分为正常运行下的控制和发生断相故障情况下的控制。其中，在正常运行下的控制策略方面，国内外学者已经取得了很多的研究成果。文献[1]提出多相坐标变换矩阵的方法，实现了六相逆变器供电的感应电机解耦控制。文献[2]利用多相坐标变换理论，首次将磁场定向矢量控制策略引入到多相电机驱动系统。而对多相电机缺相故障情况下的容错控制同样是近年来较为热门的研究方向，目前比较常用的容错控制方式大致分为两种：一种是基于电流滞环的控制策略，基于故障前后定子磁动势不变的原则，以不同的优化目标为约束条件求解出缺相后剩余相电流的参考值，然后利用滞环比较的方式进行控制。这种控制方式会带来滞环控制的固有缺点：开关频率不固定以及电流和转矩的脉动较大。另一种是在求解出剩余相绕组电流参考值的基础上，建立缺相后五相电机的数学模型，通过构造新的旋转坐标系实现电机缺相后的矢量解耦控制。这种控制方法的电流内环大多采用的还是PI控制器，但是传统的PI控制器在阶跃响应过程中会有超调，并且在对给定电流的跟随能力和动态响应上性能不高，在高功率、低电压、大电流的应用场合，PI控制器无法兼顾系统的快速响应性和稳态误差小的要求。

因此，针对六相永磁同步电机（Permanent Magnet Synchronous Motor，PMSM）一相断路容错控制中传统PI控制器的缺陷，本文将无差拍电流预测控制引入了六相永磁同步电机容错控制，提升了系统的电流环响应带宽，改善了电流的超调和快速响应性能，并通过仿真验证了方法的可行性。

1 剩余相参考电流求解

本文所述的六相PMSM拓扑结构如图1所示，两套定子绕组ABC和UVW之间电角度相移30°并以W相开路为例，缺相故障时两套绕组中性点连接且不连至逆变器端。

同时为了简化分析，对六相PMSM做出如下假设：

1）磁路线性，忽略磁滞和涡流损耗；

2）不计定子表面齿槽的影响，转子上无阻尼绕组；

3）绕组正弦分布；

4）忽略电机漏感。

本文采用基于缺相前后定子总磁势不变原则，双三相PMSM缺相前定子总磁势为[4-5]

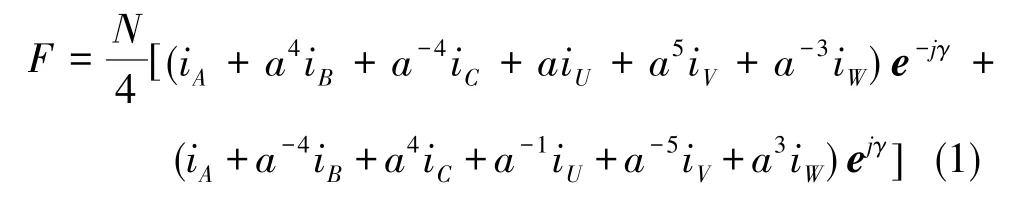
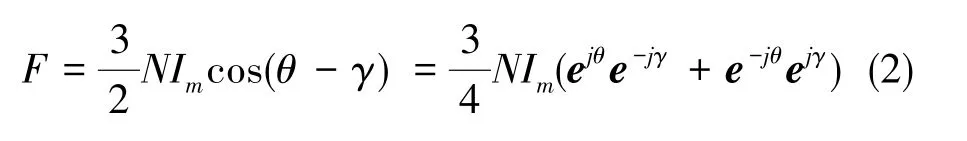
式（2）中，Im为电流的幅值，θ为A相电流相角。当W相开路时对比式（1）和式（2），为了保持定子总磁势不变，剩余五相电流必须满足

显然，对于式（5）和式（6）组成的方程组，其解并不唯一，这时一般采用最优化方法进行求解，通常使用的优化目标有两个，一是定子铜损最小，二是定子电流幅值最小。本文以定子电流幅值最小为目标，构造出如下的目标函数

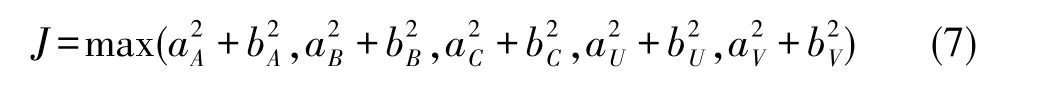
利用Matlab的最优化工具箱来求解出满足上述方程组并使得目标函数J达到最小的解，可以得到基于磁动势不变原则下以定子电流幅值最小为优化目标的六相PMSM缺相后剩余五相绕组参考电流值

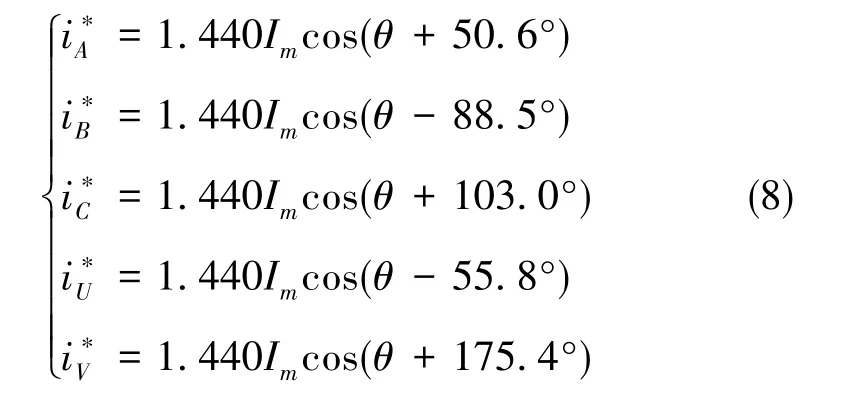
2 矢量解耦控制

2.1 变换矩阵的确定

根据矢量空间解耦的建模理论[3]，缺相后六相电机的电压、电流、磁链矢量可以通过式（9）所示的静止变换矩阵变换到一个参与机电能量转换的α-β子平面和一个只产生铜损的z1-z2-z3谐波子平面。

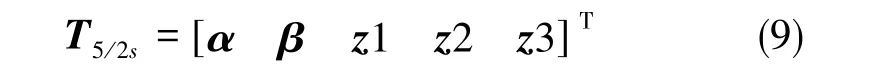
根据坐标变换的磁动势不变和功率不变原则，α、β绕组总磁势和剩余五相绕组总磁势应该相等，如式（10）所示。根据定子绕组之间的位置关系，向量α、β可以很容易确定下来。

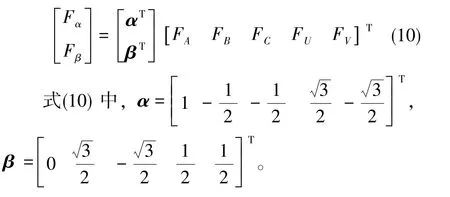
再由向量z1、z2、z3和向量α、β之间的正交关系以及电流约束条件，可以求解出式（11）所示的静止变换矩阵[6-7]

得到静止变换矩阵后，由于只有α-β子空间参与机电能量转换，因此只需对α-β子空间的变量进行Park变换。所以，从五相自然坐标系变换到两相旋转坐标系的总变换矩阵T5／2r为

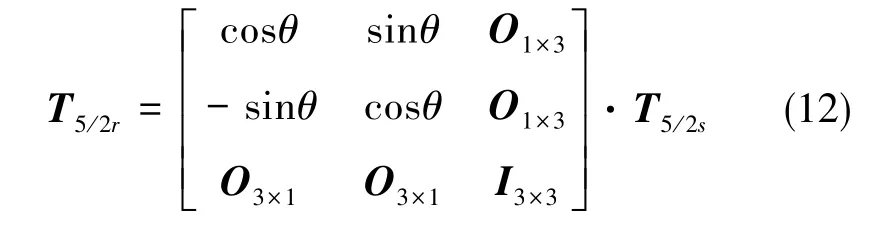
2.2 缺相六相PMSM的数学模型

电机W相开路时，剩余五相在自然坐标系下的电压和磁链方程可以写为

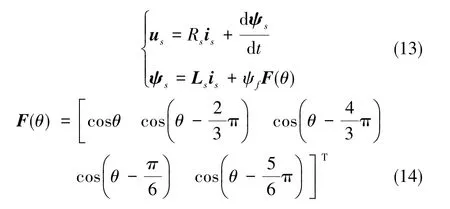
式（13）中，Rs为电机电阻，Ls为剩余五相的电感，ψf为转子磁链。对式（13）的电压和磁链方程两边同时乘以旋转变换矩阵T5／2r，得到d-q坐标系和z1-z2-z3平面下的电压和磁链方程，如式（15）和式（16）所示[8]。

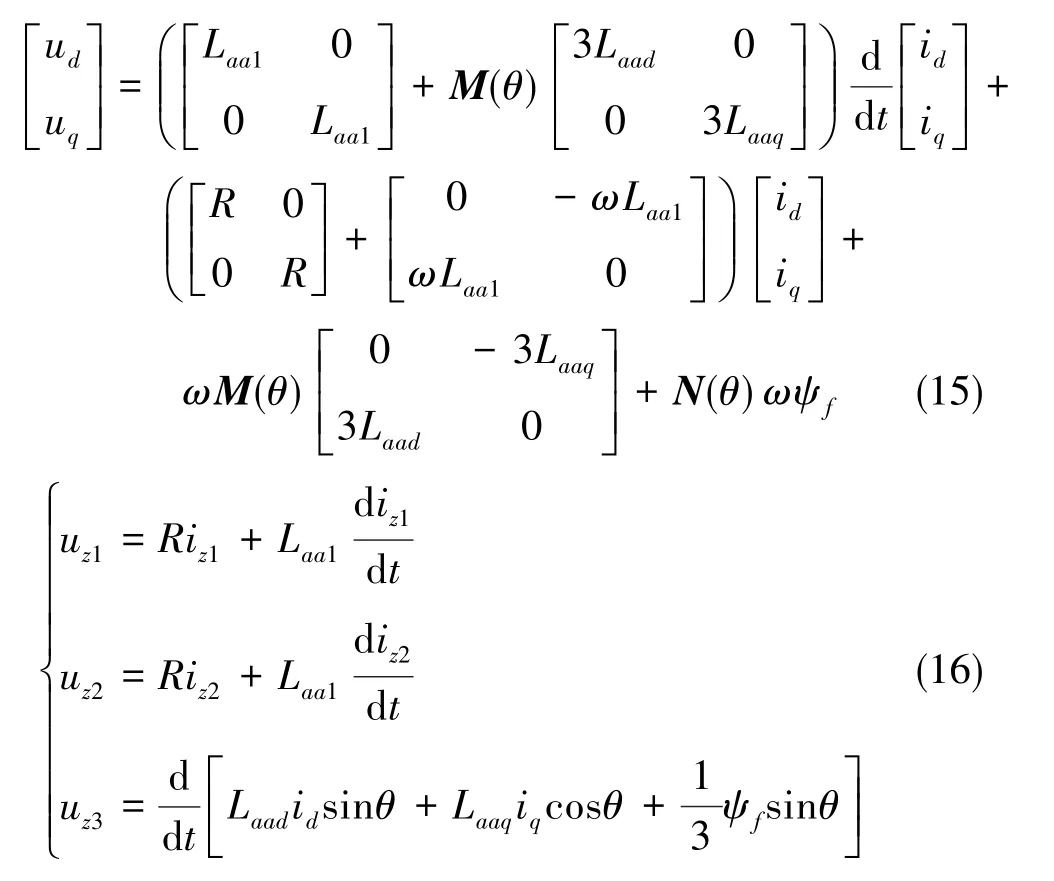
式（15）、 式（16）中， Laa1为定子绕组的漏自感，Laad和Laaq分别为d轴、q轴主自感，ω为电机转速， M（θ）和 N（θ）满足

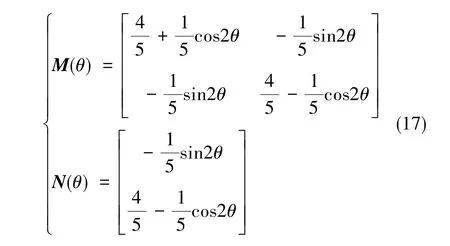
2.3 缺相后的解耦容错控制

由式（15）可知，由于电感系数矩阵和永磁体磁链投影矩阵的不对称性，导致d轴、q轴之间仍然含有较多交叉耦合项，无法直接进行矢量控制，因此需要引入新的旋转坐标系来实现解耦控制，对式（15）两边同乘 M-1（θ）， 可得

观察式（20）， 如果 Q（θ）=0， 则 m 轴、 n轴之间实现完全解耦。所以为了消除Q（θ）的影响，可以将Q（θ）视作扰动项，通过提高电流环带宽的方法来克服扰动的影响，从而实现W相开路故障下六相PMSM的矢量控制，控制系统框如图2所示。

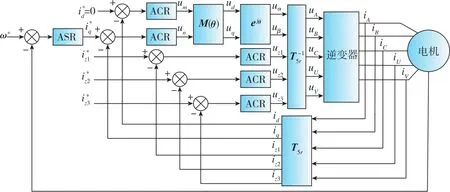
图2 缺相故障下六相PMSM矢量控制系统Fig.2 Six-phase PMSM vector control system in the case of the single-phase open circuit fault

3 无差拍电流预测控制

为了提高电流内环的跟随性能，针对传统PI控制器会产生电流超调且动态响应性能较差的缺点，对电流环采用电流预测控制，设计无差拍电流预测控制器代替PI控制器，对式（20）采用一阶Euler公式进行离散化处理并化简，可得

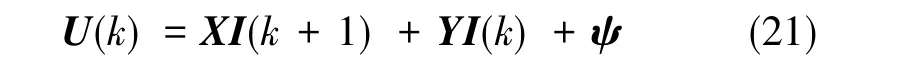
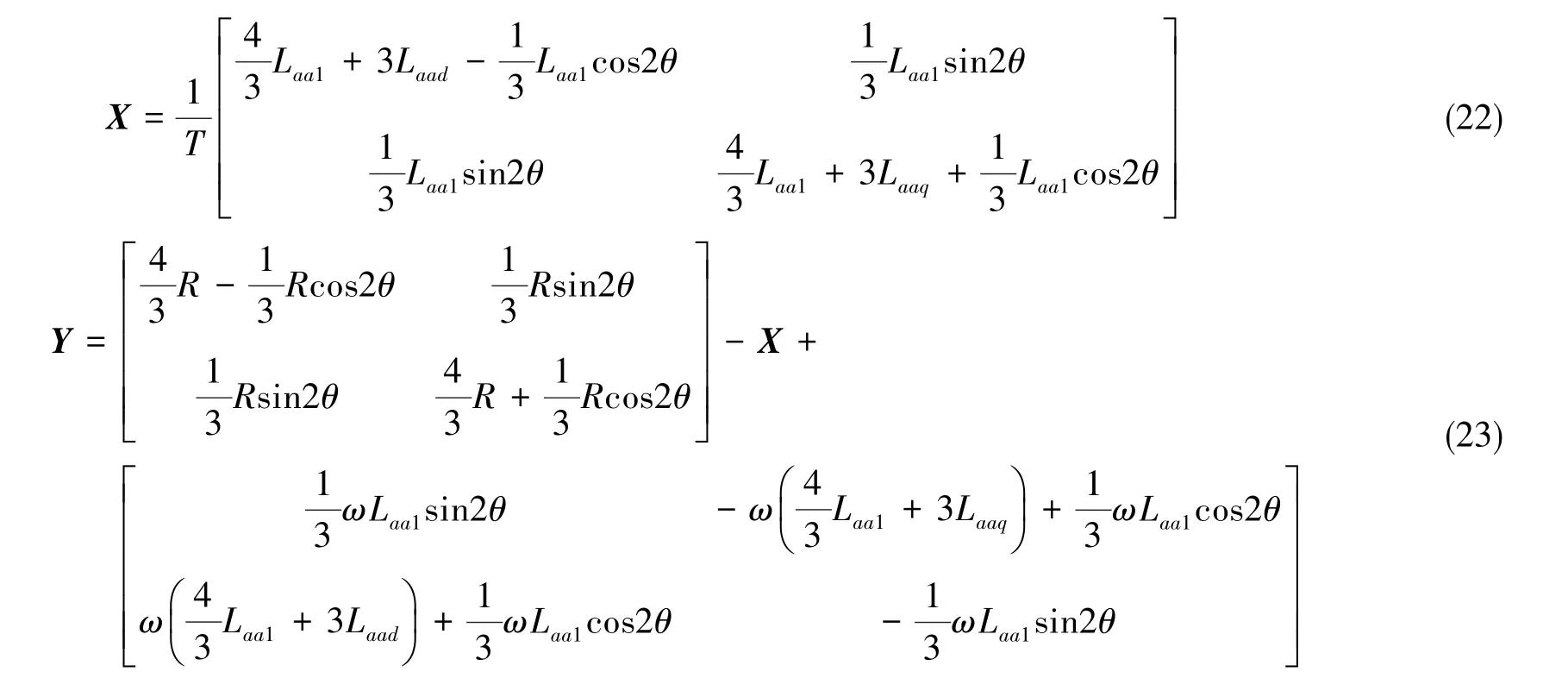
式（22）中， T采样时间。 令id（k+1）=、 iq（k+1）=， 再采样kT时刻的电流值id（k）和iq（k）， 代入式（21）中，即可计算出当前时刻应当施加的电压参考值。利用SVPWM或SPWM调制方法合成出电压参考值，在理想情况下kT～（k+1）T时刻施加在电机上的电压就是应该施加的电压参考值，从而使得（k+1）T时刻的电流值跟踪上参考电流。无差拍电流预测控制框图如图3所示。

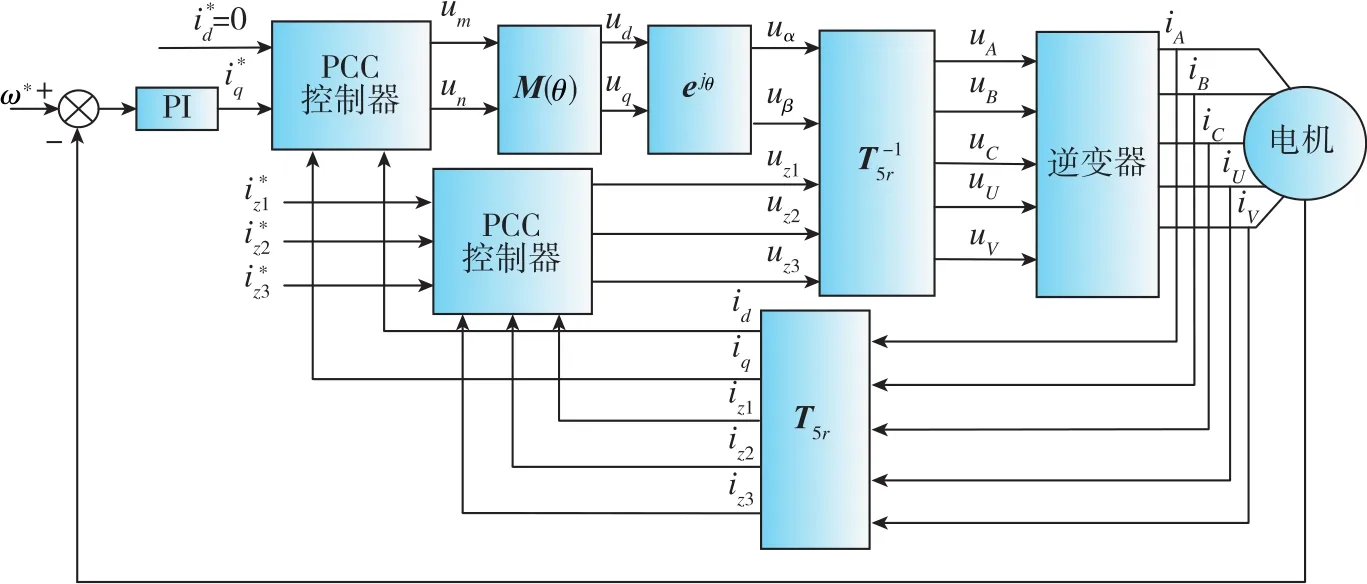
图3 一相开路六相PMSM无差拍电流预测控制系统Fig.3 Six-phase PMSM deadbeat predictive current control system in the case of the single-phase open circuit fault

在实际控制系统中，由于电流采样时刻和PWM占空比实际更新时刻存在固有的一拍延时，因此理想的无差拍控制算法应用在实际系统中需要考虑当前周期施加的电压对电流造成的影响，所以需要对固有一拍延时进行延时补偿。首先，根据当前周期施加的电压值和kT时刻的电流采样值，代入电压方程得到（k+1）T时刻的电流预测值，再利用预测的电流值来进行无差拍控制，将（k+2）T时刻希望达到的电流值用当前周期的id和iq参考值来代替，从而可以得到（k+1）T时刻应该施加的电压值。这样改进之后，理想情况下，电流在滞后两个周期后跟踪上指令值，而两拍跟踪也是目前电机实际控制系统中所能达到的最优效果。但同时这种算法对电机参数十分敏感，控制的鲁棒性较差。在实际控制系统中，需要结合在线参数辨识和自抗扰控制技术来增强算法的鲁棒性。

4 仿真结果分析

为了验证本文提出的解耦矢量容错控制方式和无差拍电流预测控制的有效性，在Matlab／Simulink中搭建系统仿真模型。电机参数如表1所示。

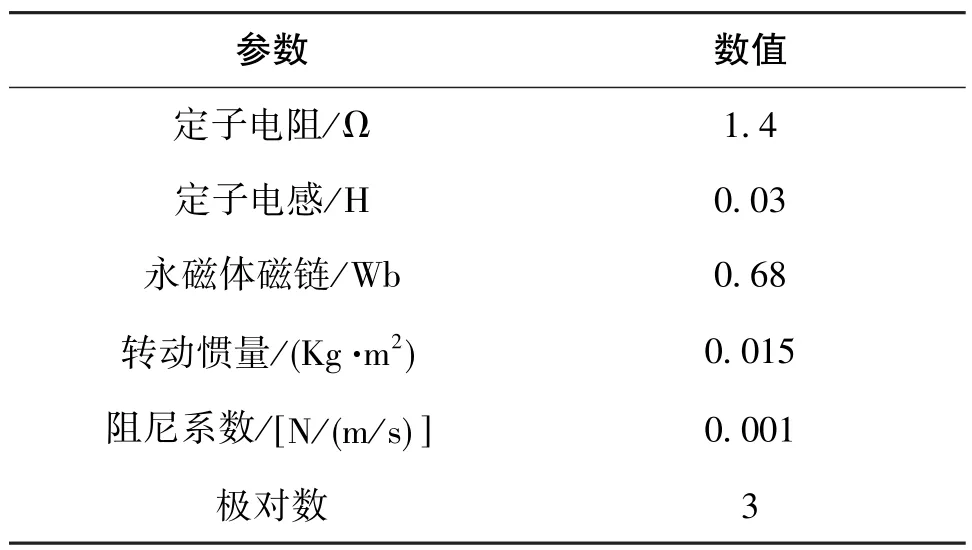
表1 电机参数Table 1 Parameters of PMSM

首先，为了验证本文提出的容错控制方式的有效性，六相PMSM正常空载起动，电机给定机械角速度设为50rad／s，0.2s时突加50N·m恒定负载，并在发生缺相故障之前采用基于双d-q坐标系下的矢量控制正常运行，在0.4s时系统发生W相断相故障，系统没有施加任何优化的容错控制方法，在0.8s时直接切换为施加本文提出的容错控制策略，采用传统PI控制器，仿真结果如图4～图6所示。

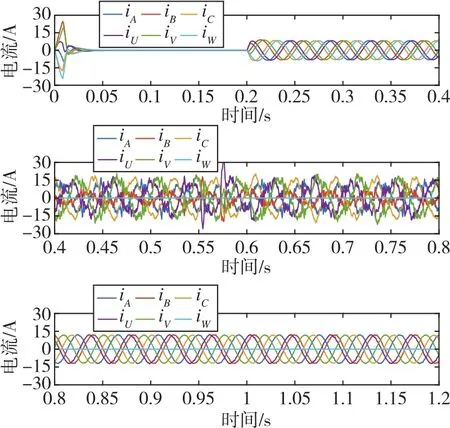
图4 定子端的六相电流曲线Fig.4 Six-phase current curves at stator end

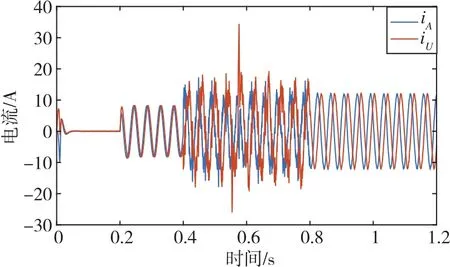
图5 定子端的A相和U相电流波形Fig.5 Current waveforms of phase A and phase U at stator end

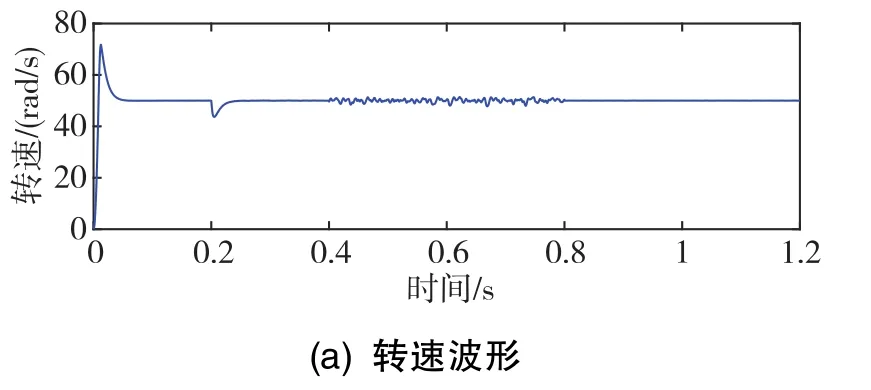
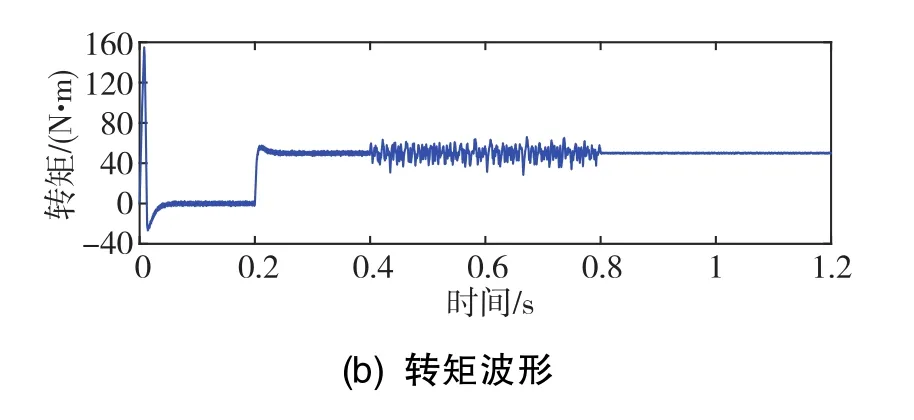
图6 转速和转矩的波形图Fig.6 Diagram of speed waveform and torque waveform

从仿真结果可以看出，在0.4s发生W相开路故障并未施加容错控制策略时，剩余五相电流均产生了不同程度的畸变和增大，并且电机转速和电磁转矩均出现波动，特别是转矩会出现明显的两次谐波分量，转矩脉动很大，这是由于缺相后导致磁场不再对称，仍然采用正常工况的控制方法无法再实现解耦的d轴、q轴电流控制，因此会有很大的谐波电流产生。而在0.8s施加了容错控制策略后，定子剩余相电流幅值近似相等，近似为正常运行时电流幅值的1.44倍，与本文采用定子幅值最小的优化目标理论分析结果相一致，并且电流谐波分量也被控制的相对较少。同时，转速和电磁转矩在施加容错控制之后得到明显改善，也进一步验证了控制策略的有效性。

接着，为了验证本文提出的无差拍电流预测控制的有效性，在电机参数和速度环参数均相同的前提下均采用id=0控制策略，使用电流预测控制器代替PI控制器，六相逆变器采用SPWM调制方式，两种控制策略的结果对比如图7～图9所示。

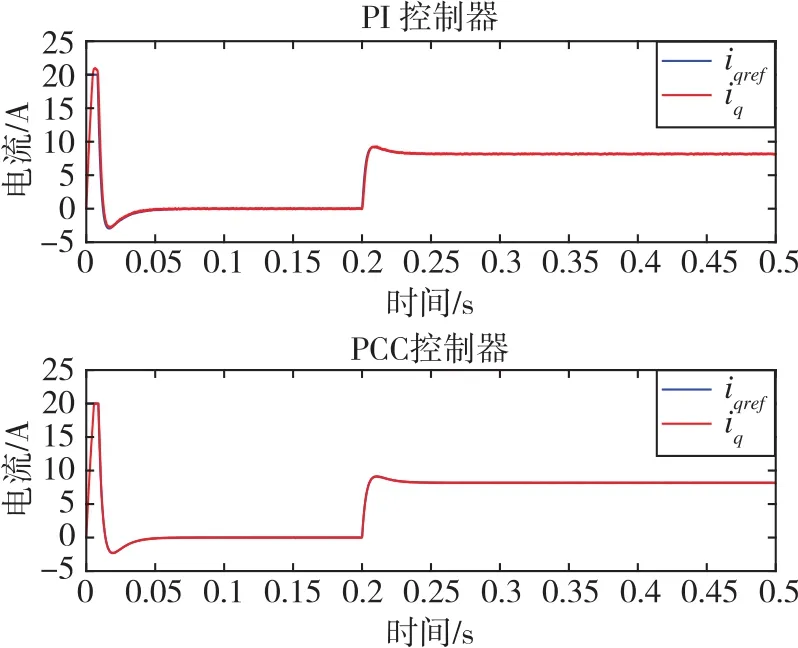
图7 PI控制下的iq跟随给定波形图Fig.7 Waveform of iqfollowing the given value under PI control

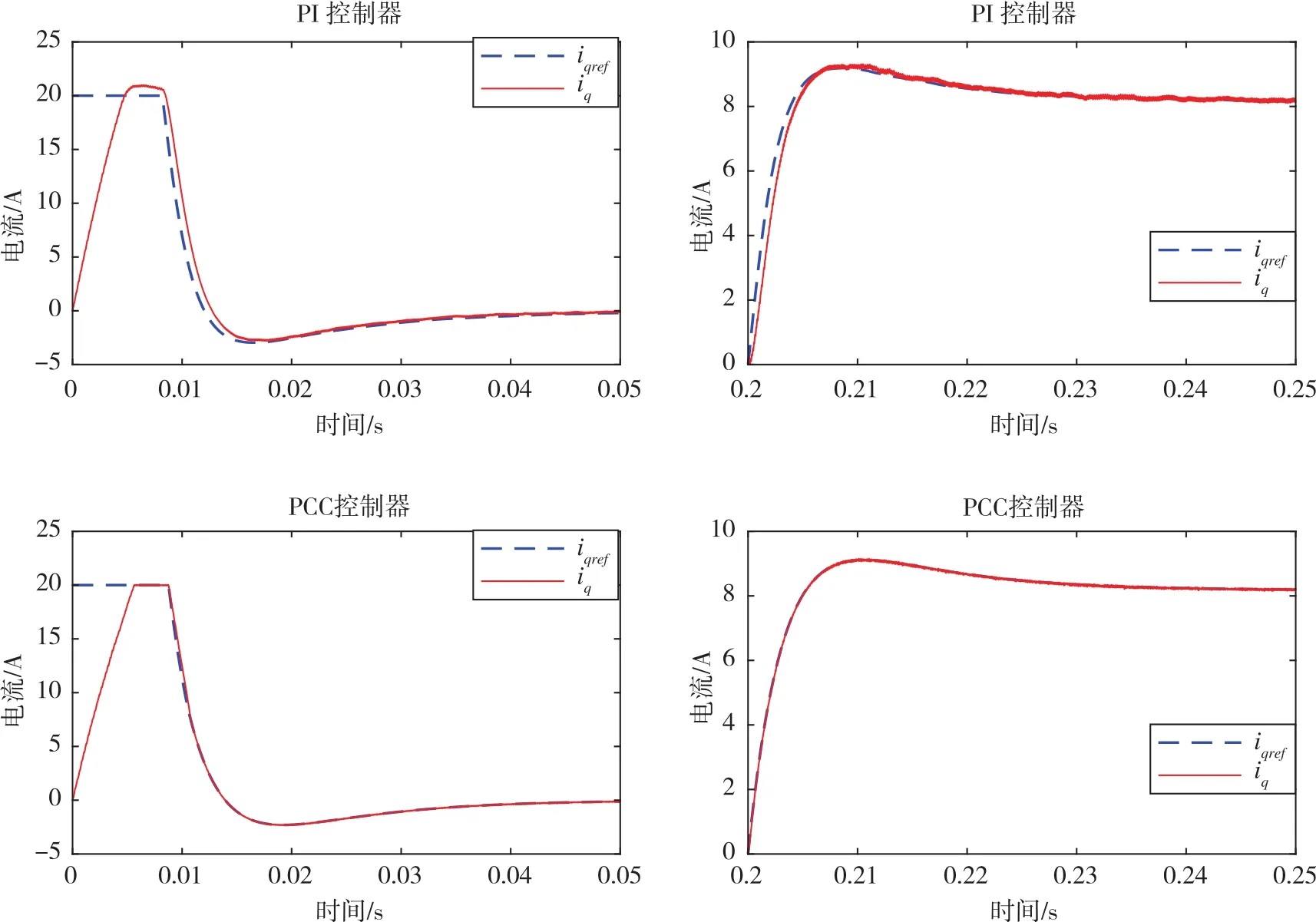
图8 PI控制下iq的局部放大图Fig.8 Partial enlarge diagram of iqunder PI control

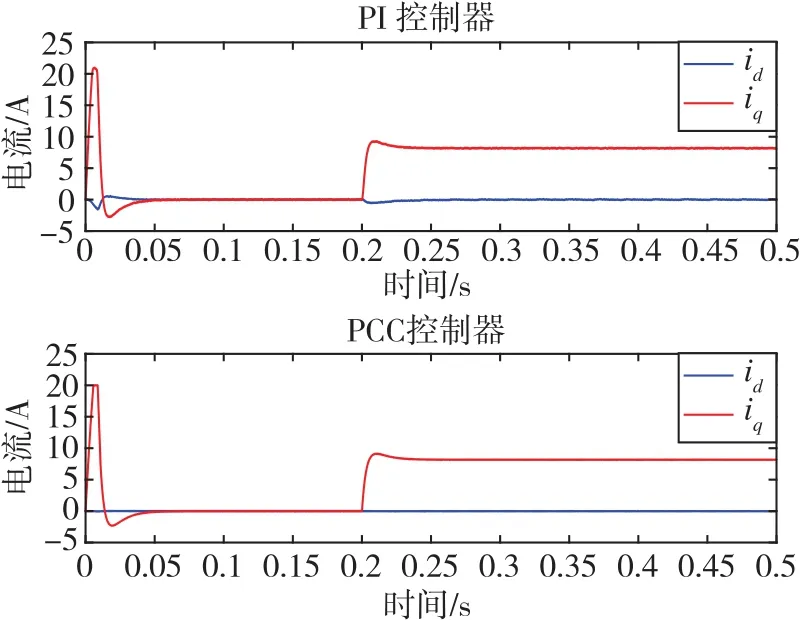
图9 id、iq波形图对比Fig.9 Comparison between idwaveform and iqwaveform

由图7、图8可知，采用PI控制器时iq总体上来说可以较好地跟随给定值，但在电机启动和突加负载转矩时会出现超调以及动态响应性能较差的问题。从图8的局部放大图对比来看，上面两张是传统PI控制的iq波形图，下面两张是采用电流预测控制器的iq波形图，可以看到无论是动态过程还是稳定后，iq都可以始终相对更好地跟随给定值，并且无超调产生。因此，采用电流预测控制器后，电流环的性能得到了改善，验证了无差拍电流预测控制算法的可行性。

5 结论

本文以中心点相连且不与逆变器端相接、两套绕组相移30°的六相PMSM为研究对象，当电机发生一相开路故障时，采用了一种基于矢量解耦的容错控制策略，为了提高电流环性能，提出了使用无差拍电流预测控制器来代替传统PI控制器，并通过仿真对比分析得到如下结论：

1）通过建立缺相后六相PMSM的数学模型并引入新的旋转坐标系来实现矢量解耦的容错控制策略，可以明显改善缺相后电机的电流畸变和转矩波动，保证电机断相之后的正常运行。

2）将无差拍电流预测控制算法引入容错控制之后，相较于传统PI控制，该算法提升了电流环跟随性能和动态响应性能，克服了传统PI控制无法兼顾快速响应和稳态性能的缺点，在电机参数准确的前提下可以达到理论上的最优控制效果。