动压气浮轴承锁紧螺母装配应力分析与改进

张翰明，郝永勤，谭映戈，朱志刚，孙亚朋

（北京航天控制仪器研究所，北京 100039）

0 引言

动压气浮轴承的常见支撑结构包括柱型、半球型、锥型和球型四种[1]，其结构示意图如图1所示。电机高速旋转时，气体由转子体和支撑轴之间的间隙泵入，形成具有一定支撑刚度的气膜，由于气膜厚度仅微米级，因此存在加工精度高、装配难度大、可靠性差等问题[2]。本文研究的目的是通过应力分析改进轴承结构，从而提高工作可靠性。

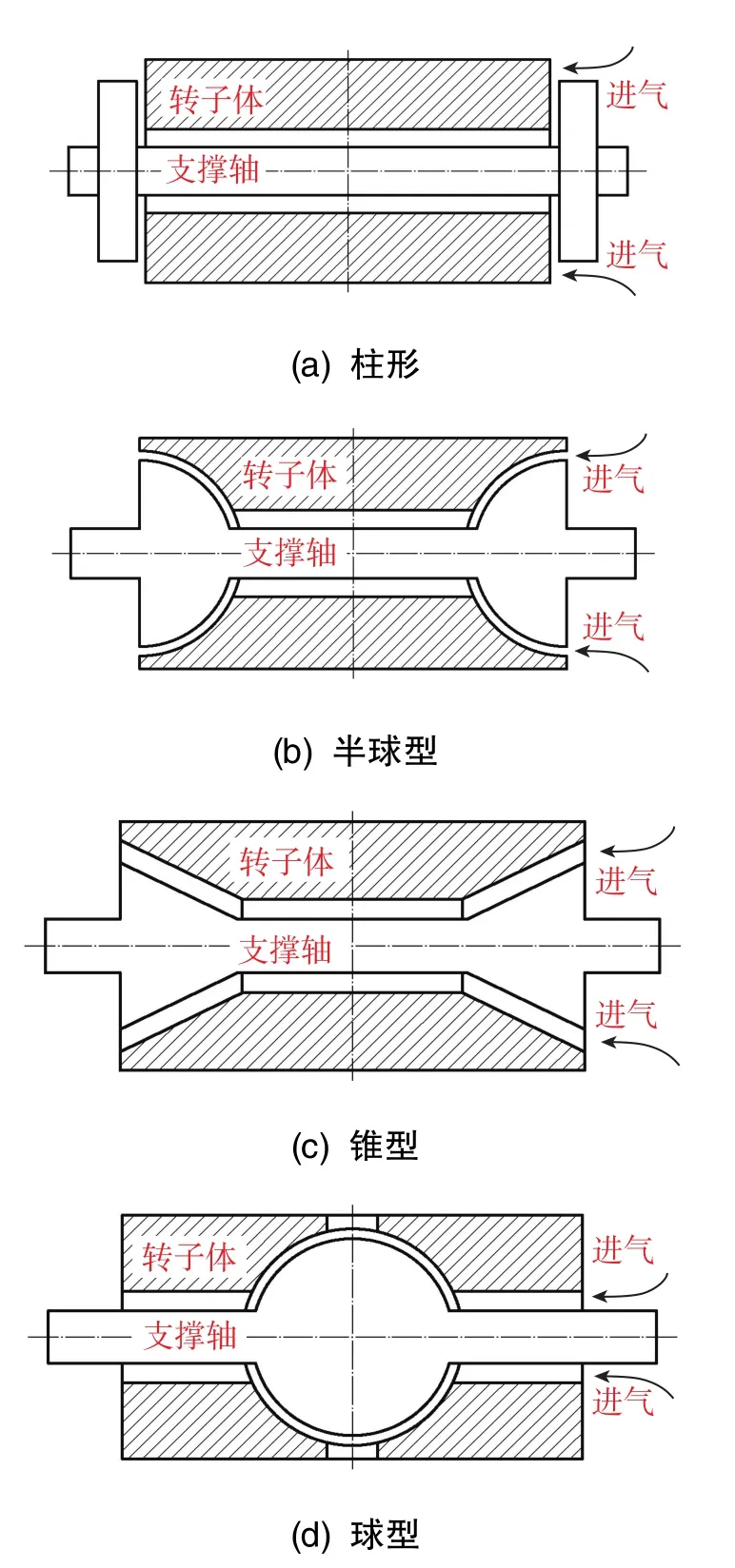
图1 动压气浮轴承常见类型Fig.1 Common types of gas-dynamic bearing

提高动压气浮轴承工作可靠性的重点在于对镀膜、刻槽、研磨、测试等关键工艺的突破。陈白帆等[3]分析了零件表面微观工艺特征对轴承工作可靠性的影响，并提出了改善制造工艺设计的思路。王晓瑜等[4]分析了研具对零件成型精度的影响，提出了研具设计准则，并通过试验验证了设计方法的正确性。王京锋等[5]提出了以反力矩测试曲线作为可靠性筛选的手段，并分析了反力矩测试曲线的原理和方法。任同群等[6]研制了轴承间隙自动测量设备，详细介绍了设计方案和工作原理，实验证明了综合测量精度优于0.3μm。刘晶石[7]研究了几种常见装配误差与干扰力矩的关系，提出了减小装配误差的合理化参数。

目前，在关键工艺研究中对装配应力的研究还比较少。生产中发现，若轴承锁紧螺母的预紧力不足，在振动、冲击等过载测试中螺母容易出现松动，使轴承间隙发生变化、转子震荡增加，严重情况下可能导致电机失步；若螺母预紧力过大，则会导致球面变形，轴承间隙同样会发生变化[8]。因此，要综合考虑螺母预紧力对轴承性能的影响，既要控制半球变形，又要保证过载条件下不松动[9]。针对半球型气浮轴承装配应力导致球面变形的问题，本文首先通过建立螺纹连接简化模型分析预紧力传递关系，然后利用有限元仿真软件得到半球零件圆度变化，并通过实验验证仿真结果，最后提出有利于提高工作可靠性的结构改进方案。

1 螺纹连接的预紧力分析

如图2所示，半球通过轴端螺母固定，将螺纹简化为围绕圆柱的斜面，将螺纹连接面展开为由斜面和滑块组成的简化模型[10]，分析螺纹连接的三个过程。

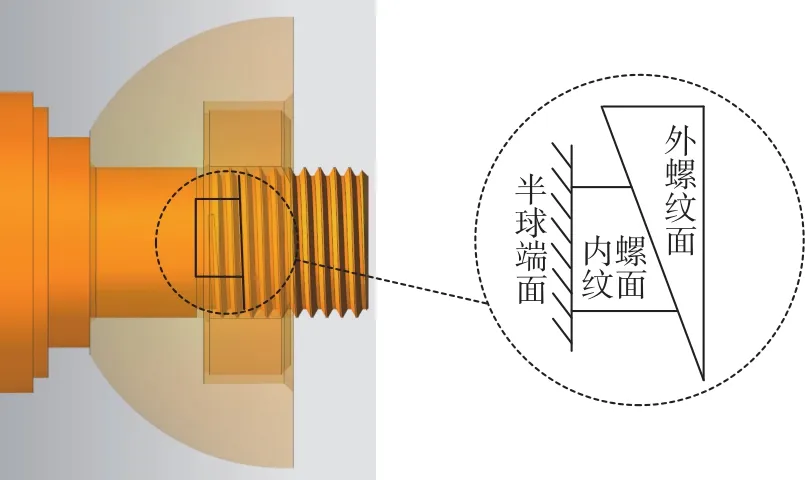
图2 螺纹连接简化模型Fig.2 Simplified model of threaded connection

（1）紧螺母过程

如图3所示，螺母端面与半球端面接触后产生挤压，即预紧力FQ；内外螺纹间存在沿斜面上升趋势V，外螺纹对内螺纹产生法向压力FN和摩擦阻力μWFN，合成总反力FR；拧紧过程中扳手力矩需要同时克服螺纹接触面间的摩擦阻力μWFN和半球端面对螺母端面的摩擦阻力Fd， 存在关系式

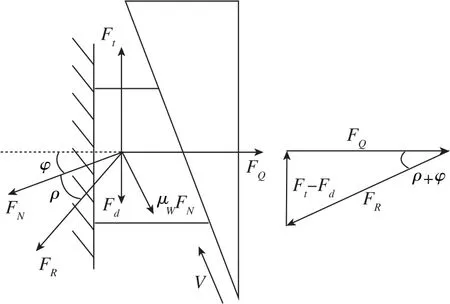
图3 紧螺母受力关系示意图Fig.3 Schematic diagram of locknut force relationship

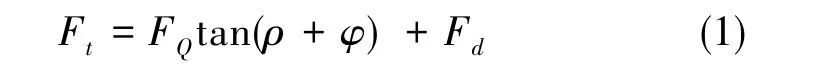
式（1）中，Ft为旋转螺母的水平推力，ρ为FR与FN之间的夹角（当量摩擦角），φ为螺纹升角。

（2）自锁过程

如图4所示，释去扳手力矩后螺母停留在原处，此时螺母存在沿斜面下滑趋势V，螺纹接触面间产生与运动趋势反向的摩擦阻力μWFN，法向压力FN与μWFN合成总反力FR，FR与预紧力FQ合成对螺母的推力Ft，维持螺母不松动。当ρ＞φ时，达到自锁状态。

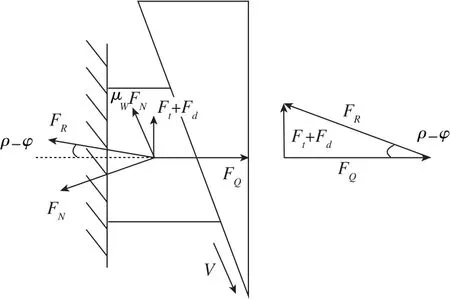
图4 自锁受力关系示意图Fig.4 Schematic diagram of self-locking force relationship

（3）松螺母过程

如图5所示，松螺母时扳手力矩要同时克服螺纹接触面间的摩擦阻力μWFN和螺母端面对半球端面的摩擦阻力Fd， 松螺母瞬间静摩擦转变为动摩擦，松螺母瞬间按静摩擦计算，存在关系式

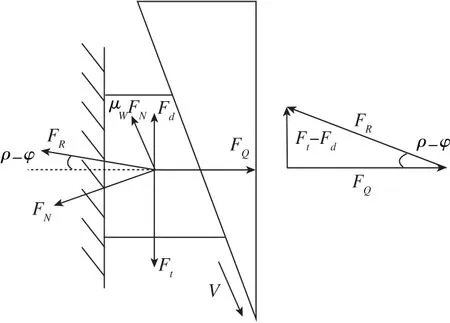
图5 松螺母受力关系示意图Fig.5 Schematic diagram of loosenut force relationship

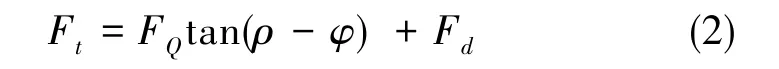
考虑到螺母端面的摩擦阻力Fd， 松螺母时扳手施加的合力矩为

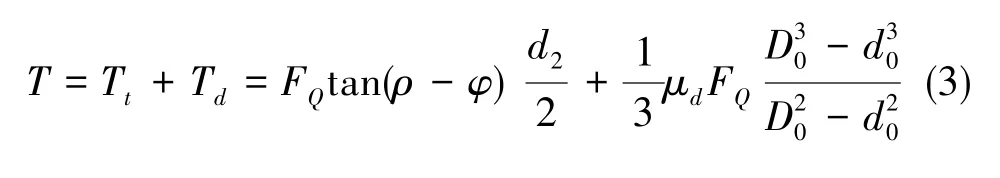
通过测量扳手力矩值可以推算螺纹预紧力，实测得松螺母力矩在60N·cm～70N·cm之间。计算中假定螺母端面与半球端面摩擦系数μd=0.1、当量摩擦角ρ=6°，由图纸得到螺纹中径、螺纹升角、螺母外径等尺寸参数，计算紧螺母力矩20N·cm～70N·cm范围内对应的预紧力值如表1所示。后续将预紧力值作为输入载荷，研究不同预紧力作用下的半球结构变形。

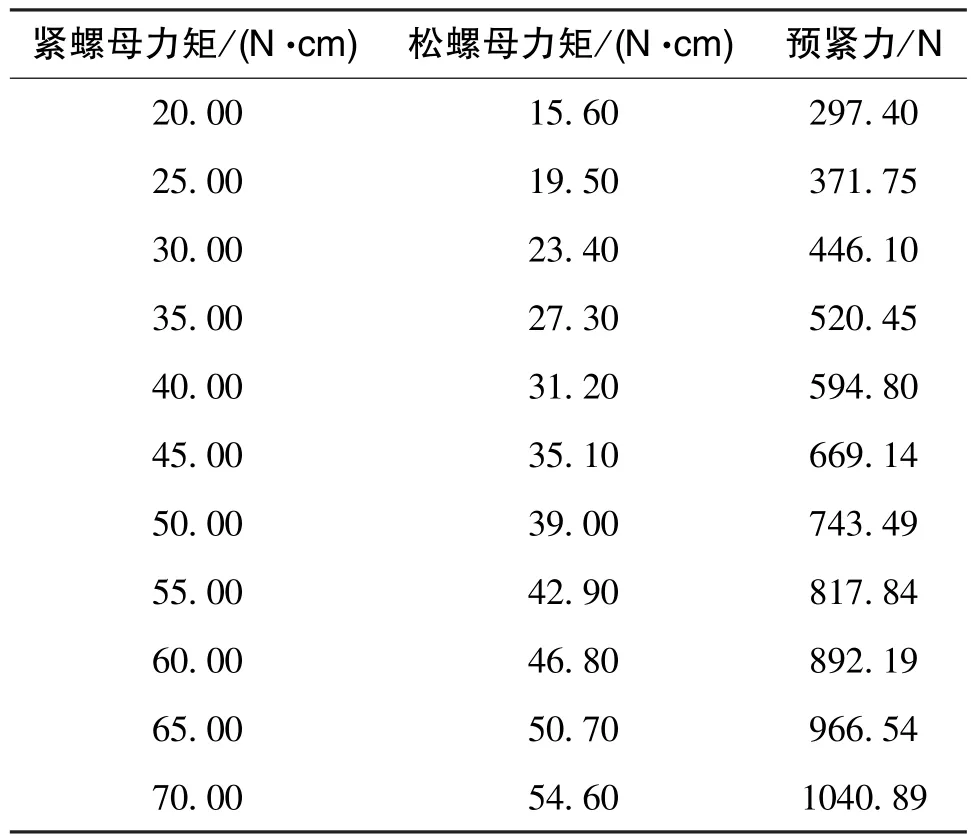
表1 螺母力矩与预紧力的关系Table 1 Relationship between torque and preload of nut

2 有限元模型建立

半球型动压气浮轴承为对称结构，为简化计算，建立由单个半球、螺母和半轴组成的三维模型，导入ANSYS Workbench进行结构静力学分析。定义材料属性如表2所示，模型约束与载荷条件如图6所示，模型网格划分质量如图7所示。

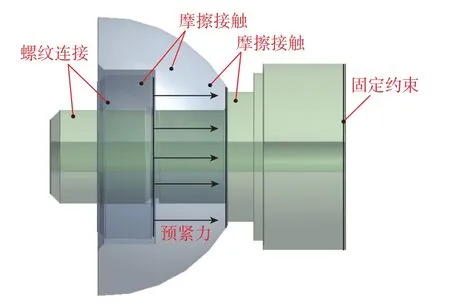
图6 模型约束与载荷条件示意图Fig.6 Diagram of boundary conditions and load of the model

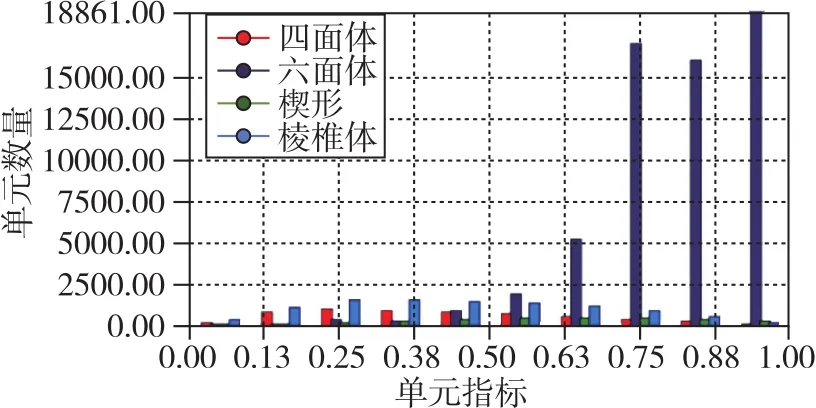
图7 网格划分质量示意图Fig.7 Diagram of meshing quality

表2 材料属性Table 2 Material properties

3 预紧力作用下的轴承结构变形

3.1 支撑轴的变形

支撑轴的轴肩与半球小端面贴合，在螺母预紧力作用下产生挤压变形，螺母预紧力743.49N作用下的轴肩应力分布如图8所示。半球小端面与轴肩贴合面积为15.57mm2，理论计算应力为47.75MPa，图8中轴肩接触面应力值集中在36.07MPa～50.50MPa之间，与理论计算基本一致。

图8 轴肩应力分布示意图Fig.8 Diagram of stress distribution on shaft shoulder

在743.49N预紧力作用下支撑轴Z向（轴向）的位移变化如图9所示，轴肩的轴向压缩变形集中在0.317μm～0.476μm之间。半球小端面挤压轴肩，轴肩外圆直径小于半球小端面外圆直径，轴肩受到不均匀挤压，导致轴肩靠近外圆处变形更大。

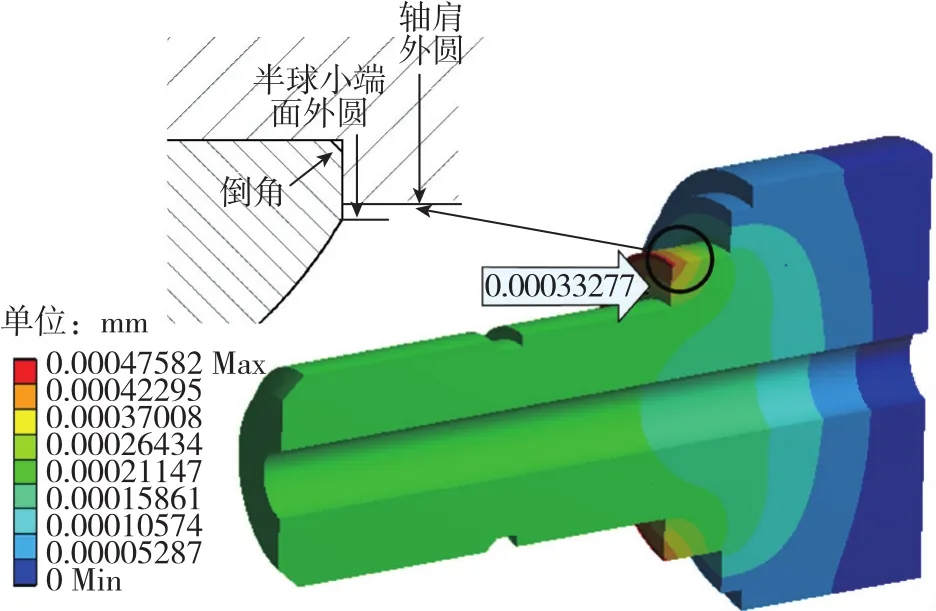
图9 轴肩位移变化示意图Fig.9 Diagram of displacement variation on shaft shoulder

3.2 半球的变形

半球在螺母预紧力作用下发生变形，其中的轴向变形为支撑轴变形和半球轴向变形之和。分别用两个正交方向的轮廓母线和四个不同直径的截面圆在受力前后的节点位移变化量表征半球整体变形情况，轮廓母线和截面圆的位置如图10所示。X向轮廓母线指向螺母侧边的平面缺口，四个截面圆距半球大端的距离分别为0.4mm、2.4mm、4.0mm、6.6mm。

图10 轮廓母线和截面圆位置示意图Fig.10 Position diagram of generatrix and circular section

（1）两条轮廓母线的节点位移

在743.49N预紧力作用下，图10中两条轮廓母线的轴向位移如图11所示。两条母线节点的轴向位移最大值均出现在中间区域，螺母侧边的两个平面对半球轴向位移有一定的影响。对比可见，X向轮廓母线的轴向位移略小于Y向轮廓母线的轴向位移。

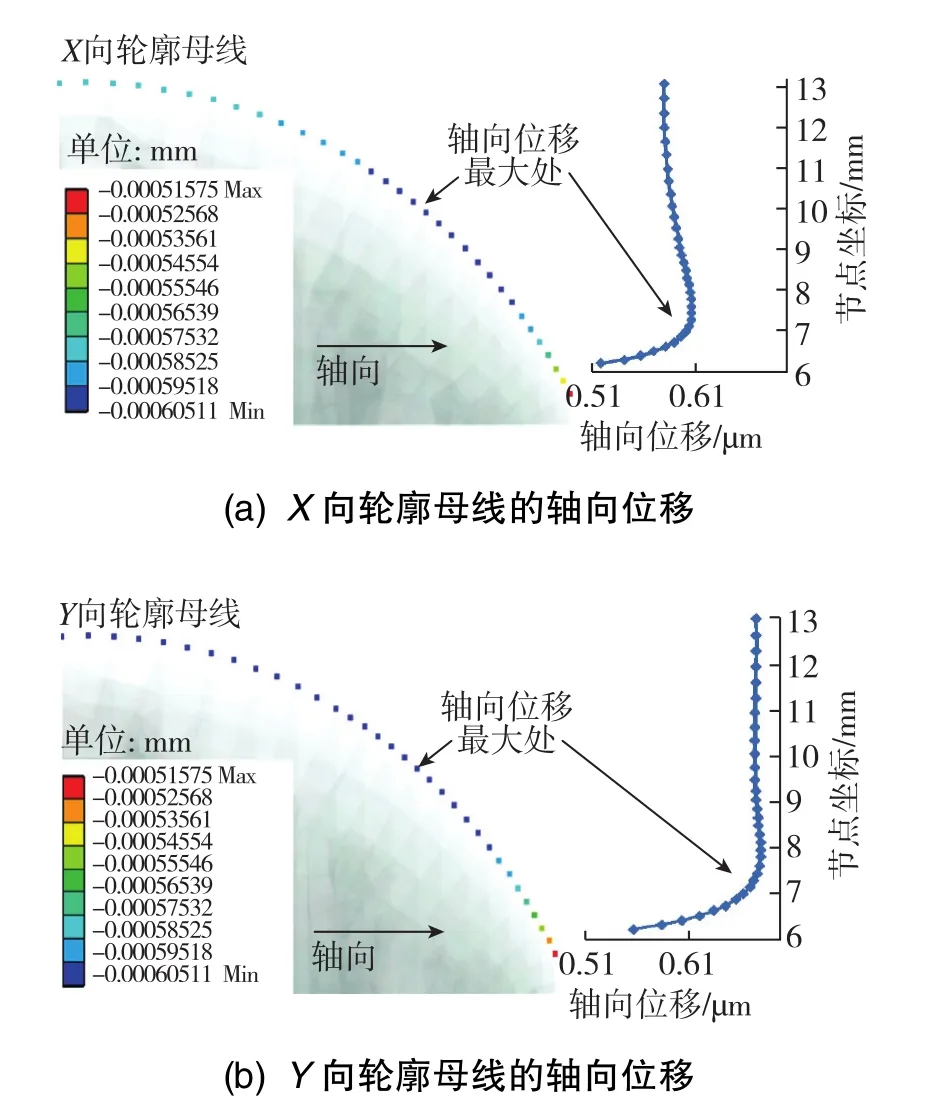
图11 轮廓母线的轴向位移Fig.11 Axial displacement of generatrix

两条轮廓母线的径向位移如图12所示。半球中间区域的径向位移变化同样比较明显，位移变化量约0.02μm。X向轮廓母线在大端处径向位移减小约0.05μm，Y向轮廓母线在大端处径向位移增大约0.03μm，大端边缘沿圆周方向趋于椭圆。

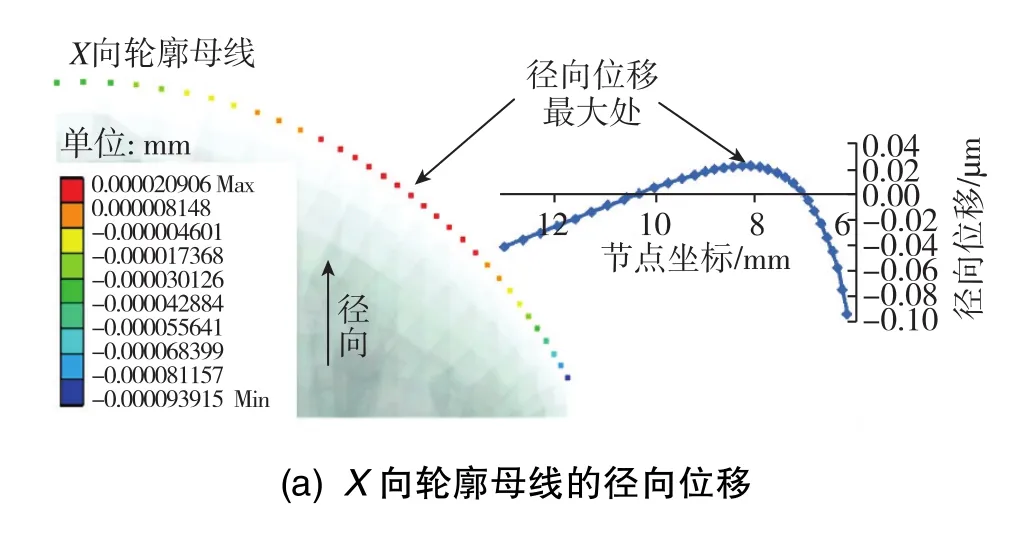
图12 轮廓母线的径向位移Fig.12 Radial displacement of generatrix

（2）四个截面圆的节点位移

最小二乘圆法是GB／T 7234-2004《产品几何量技术规范（GPS）圆度测量——术语、定义及参数》中规定的4种圆度评定方法之一，该方法具有理论成熟、算法简便的优点[11]。此处采用最小二乘圆法对比图10中四个截面圆受743.49N预紧力前后的圆度变化，设截面圆上各节点极坐标为Pi（ri， θi）（i=1， 2， …， n）， 最小二乘圆的圆心直角坐标为G（a，b），最小二乘圆的半径为R，计算公式为

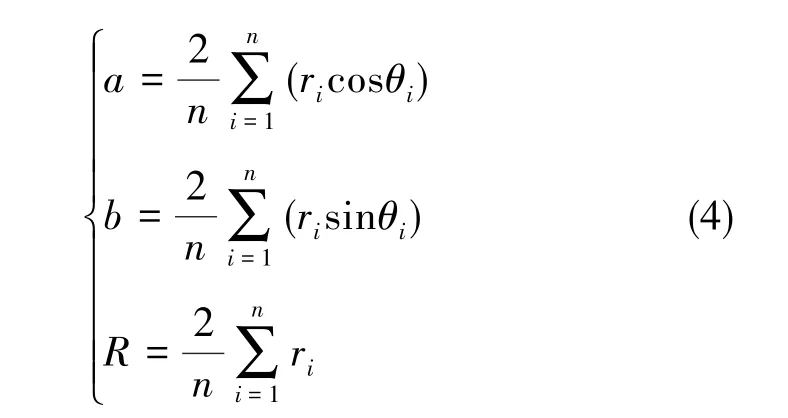
式（4）中，n为节点总数，i为节点序号。由式（4）求最小二乘圆的圆心坐标G（a， b）和半径R，得到圆度的最小二乘评定结果为

式（5）中，Rmax、Rmin分别为截面圆上各节点到最小二乘圆心距离的最大值和最小值。根据式（4）和式（5）用Matlab编程计算圆度，结果如图13所示，由小端至大端四个截面圆的圆度分别为0.021μm、0.021μm、 0.050μm、 0.030μm。 图13（d）中 Y 向的径向变形大于X向，这是由于螺母侧边的圆面对半球的挤压大于平面，导致大端截面圆趋于椭圆。

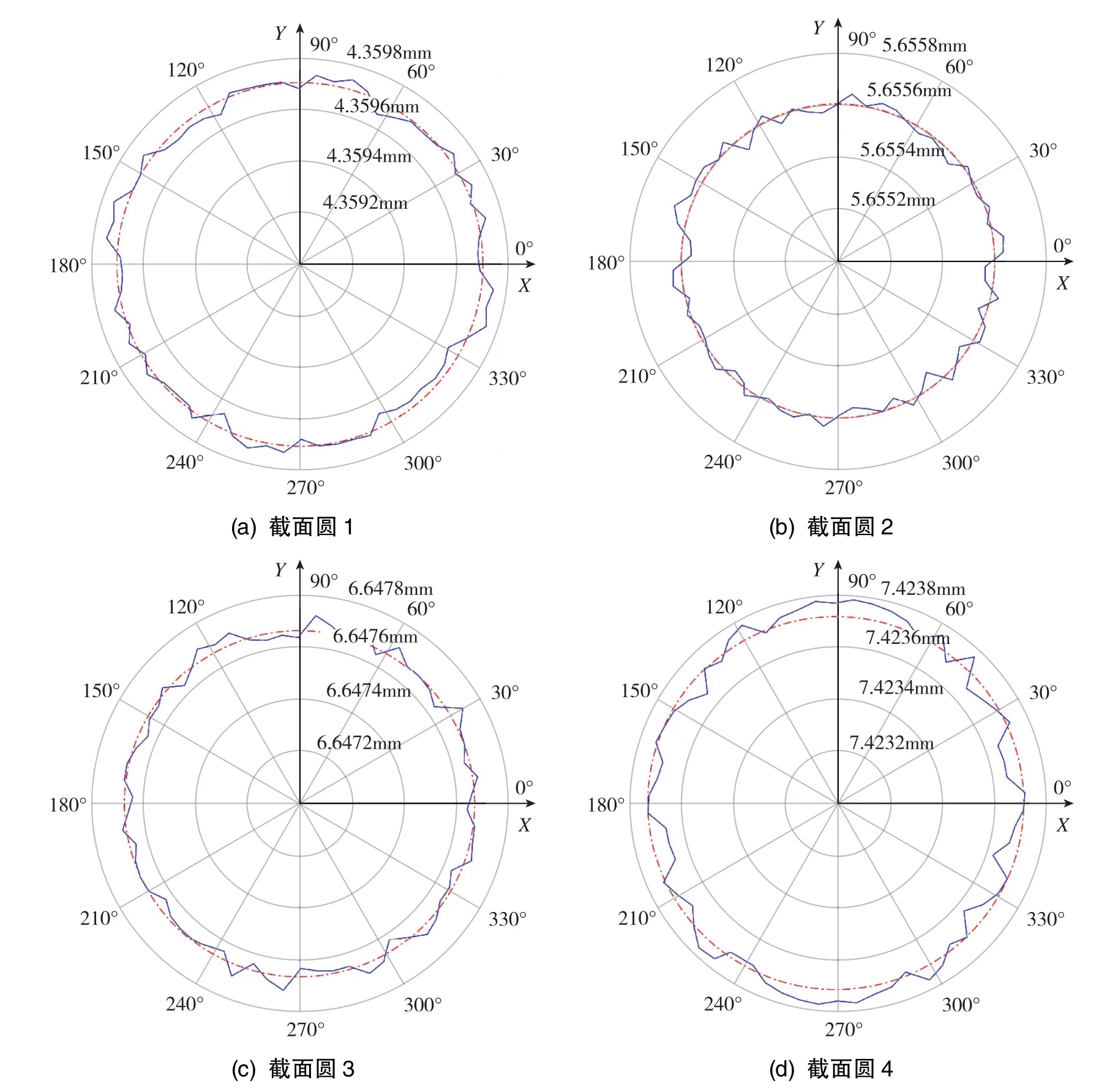
图13 四个截面圆的圆度Fig.13 Roundness of four circular sections

为进一步说明受力后半球轮廓的变化，将节点受力后的径向位移扩大10000倍对比受力前后截面圆的变化，具体如图14所示。其中，蓝线为受力前状态，红线为受力后状态，小端的截面圆1受力后沿径向收缩，中间的截面圆2和截面圆3受力后沿径向扩大，大端的截面圆4受力后趋于椭圆，这表明半球大端更容易受预紧力影响导致圆度下降。

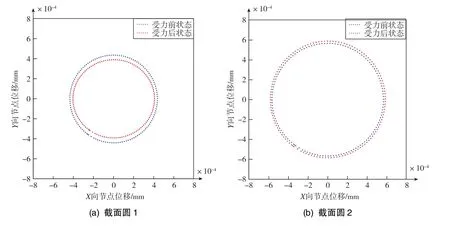
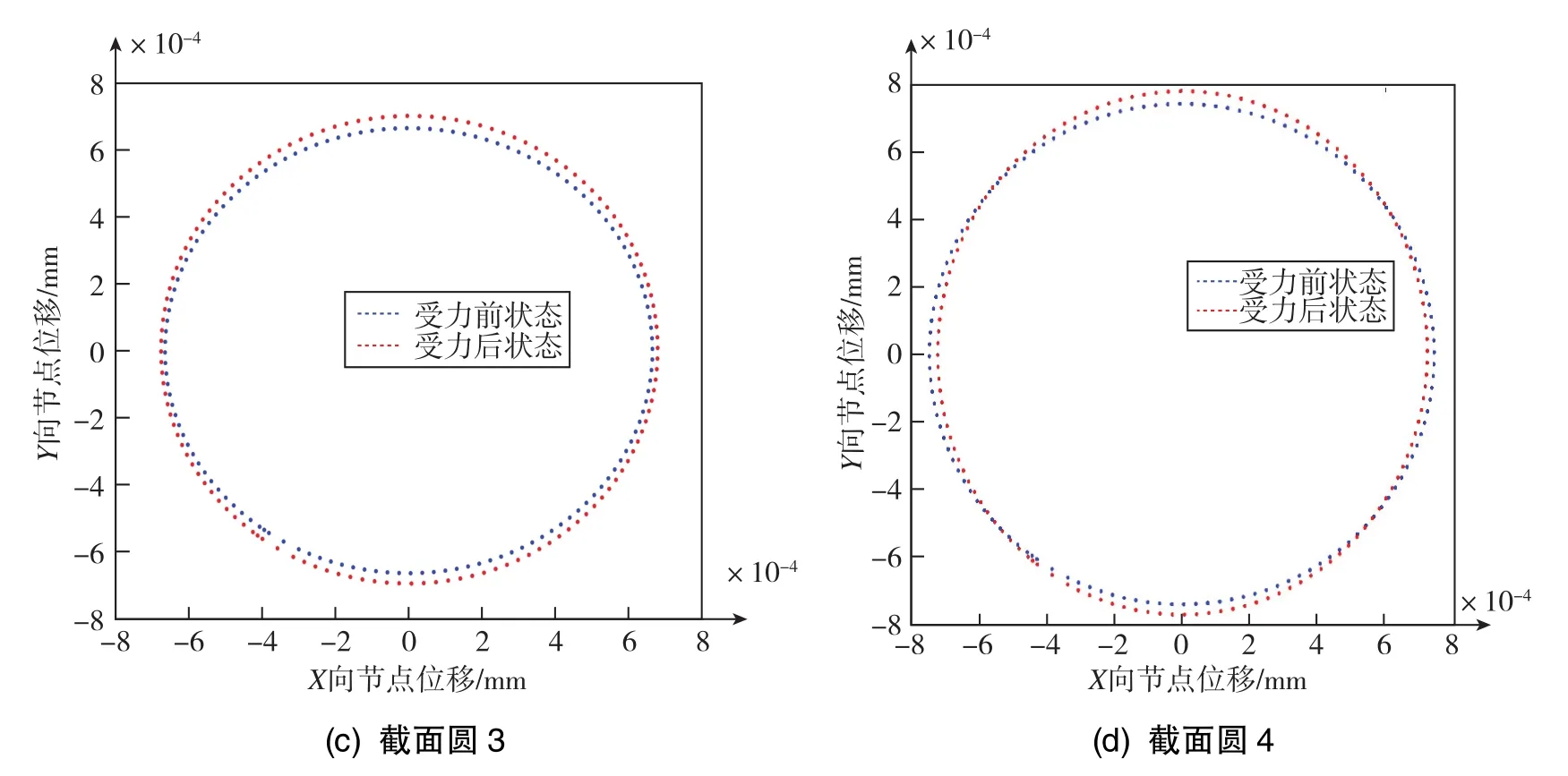
图14 四截面圆受力前后径向变形对比Fig.14 Comparison of radial deformation of four circular sections before and after stress

3.3 螺母力矩和圆度误差的测量实验

国内外通用的螺栓预紧力测量方法有扭矩扳手法、电阻应变片法、光弹法和磁敏电阻法[12]。扭矩扳手法操作简便，在装配生产线中得到广泛应用，但是要保证螺纹具有较高的加工精度和较好的润滑条件[13]。电阻应变片法能够直接测量被连接件接触面间的压应力，是一种精度较高的测量方法。光弹法用透明材料制作零件模型，模拟实际受力状态，是实验室测量方法。磁敏电阻法抗干扰能力强，适合在恶劣环境中应用，但精度不高。

半球与轴肩的接触面积仅为15.57mm2，很难通过电阻应变片直接测量。根据上述螺纹连接的预紧力分析可知，螺母预紧力可依据松螺母或紧螺母力矩计算得到，其中的螺纹中径、升角、外径、轴孔直径是确定值，摩擦系数、当量摩擦角与材料属性、加工精度、润滑条件有关。在难以测定铍材和中密度合金之间摩擦系数的情况下，参考同种钢材料的静摩擦系数对μd取值，并通过测量螺母力矩验证取值合理性。

采用数显扭力矩螺丝刀测量松螺母和紧螺母力矩，在20N·cm～70N·cm范围内测量6组数据，测量结果与计算结果数据对比如图15所示，两组数据均线性增加，偏离度较小。实验表明，摩擦系数和当量摩擦角选取合理，能够反映螺母的实际受力情况。另一方面，使用形状测量仪测量图9所示四个截面圆的圆度，测量实验如图16所示，所得测量值与仿真值对比如表3所示，测量值略大于仿真值，相差约0.01μm。

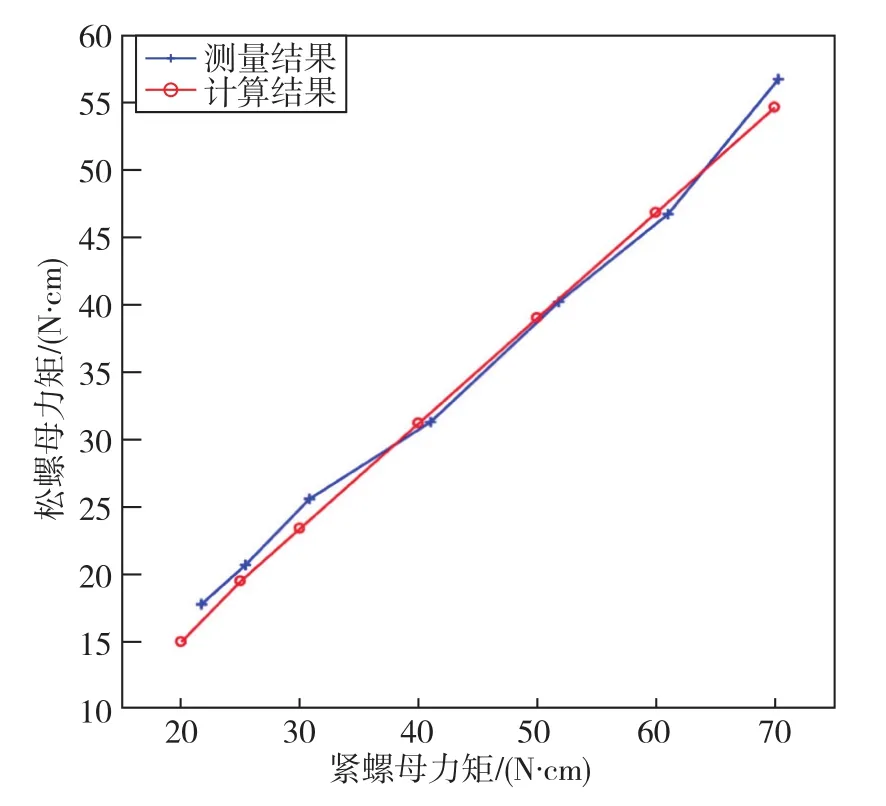
图15 螺母力矩计算与测量结果对比Fig.15 Comparison between calculating and measuring results of nut torque

图16 圆度测量实验Fig.16 Diagram of roundness measurement experiment

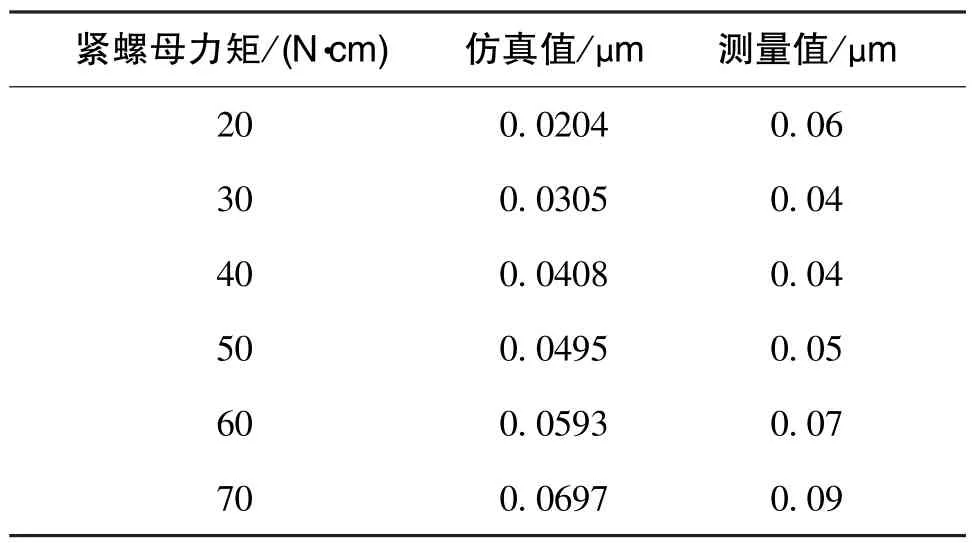
表3 圆度测量值与仿真值对比Table 3 Comparison between measuring and simulating results of roundness

4 锁紧螺母的结构改进

以上分析表明，半球与螺母之间的接触面为非圆面会导致半球受挤压后趋于椭圆，为此提出锁紧螺母结构改进方案，结构改进前后的对比如图17所示。

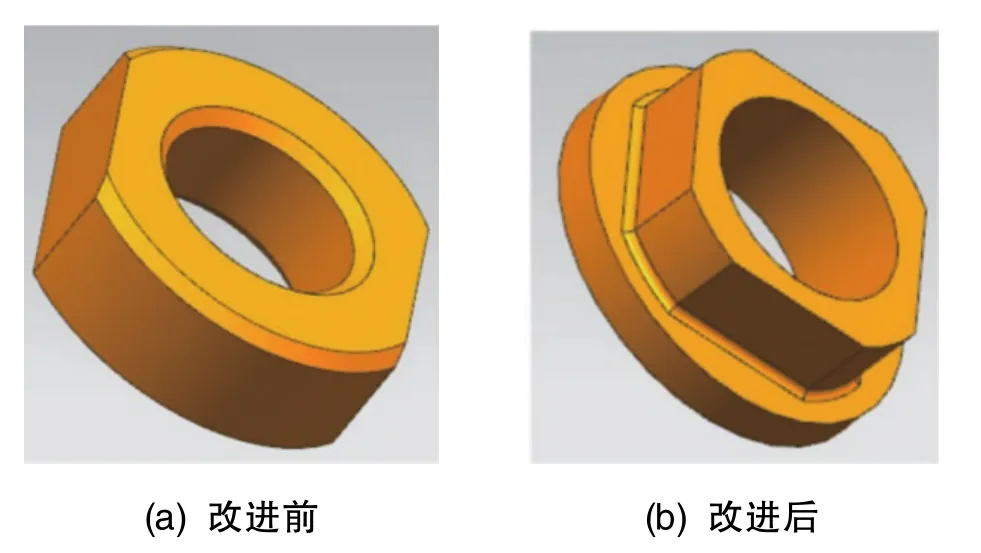
图17 螺母结构改进前后对比Fig.17 Comparison of nut structure before and after optimization

改进后螺母与半球接触面变为圆面，将图6模型中的螺母替换为图17（b）中的圆螺母，约束与载荷条件不变。两种螺母结构在同时产生743.49N预紧力时的整体变形云图如图18所示，其中的支撑轴被隐藏。图18（a）中的半球面圆周方向变形不均匀，球面轮廓处取两节点，位移约1.1μm，装配后表现为半球截面的圆度下降；图18（b）中的半球面圆周方向变形均匀，球面轮廓处取两节点，位移约0.99μm，主要变形是半球受到挤压后产生的轴向压缩和径向膨胀。由此可见，改进后螺母预紧力对半球圆度影响减小。

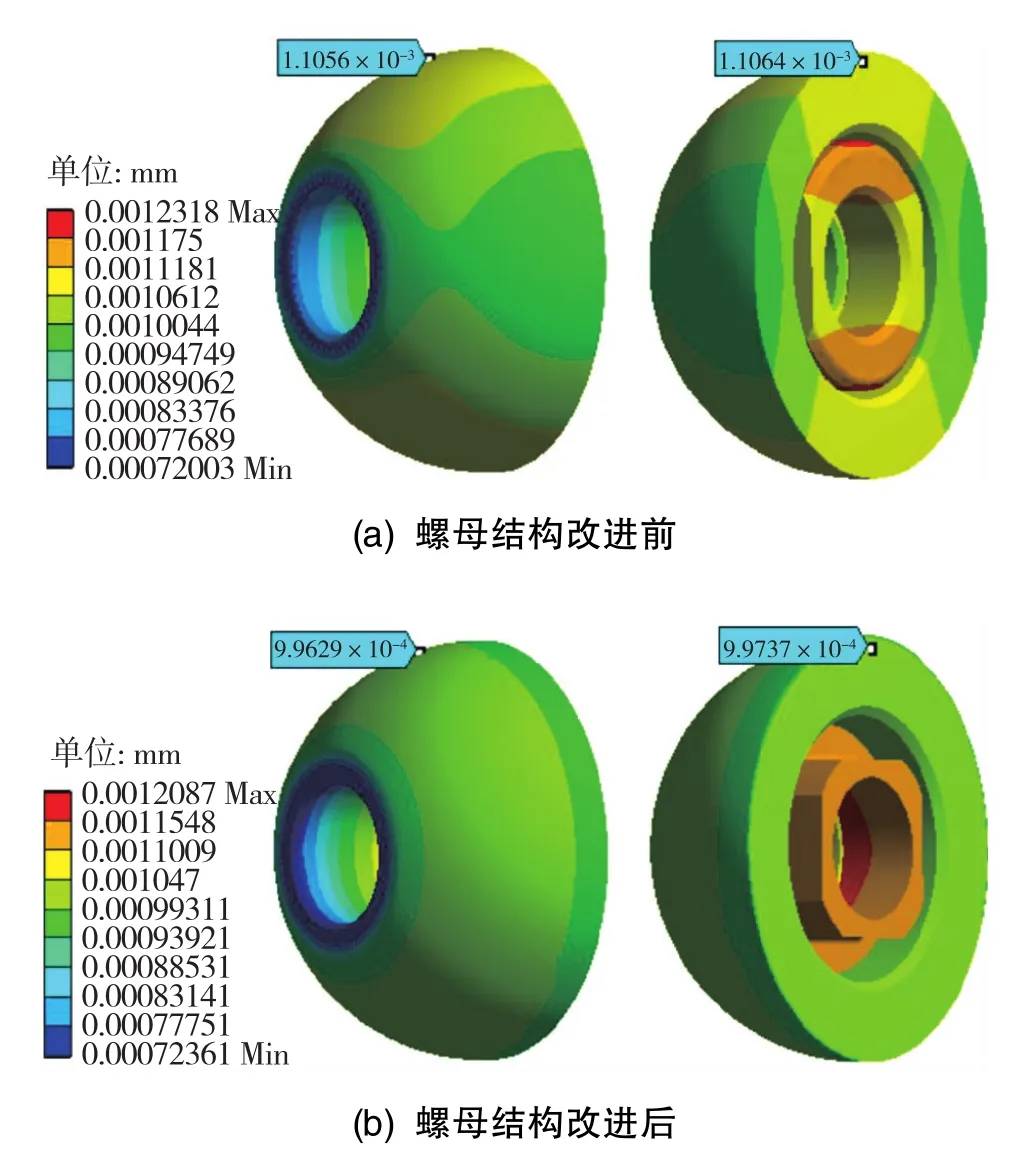
图18 螺母结构改进前后的变形云图Fig.18 Deformation nephogram of nut structure before and after optimization

5 结论

动压气浮轴承是支撑微小型电机高速旋转的重要组件，在半球零件起停过程中容易受到磨损，是影响可靠性的薄弱环节。在保证加工精度的同时，从装配应力角度研究螺纹紧固件在预紧后的变形分布，通过结构改进消除不利影响，对生产实际具有指导作用。研究得出以下结论：

1）通过建立螺纹连接结构简化模型，将螺纹紧固过程细化为紧螺母、自锁、松螺母三个阶段，分析扭力矩与螺母预紧力之间的转化关系，为有限元仿真中螺纹连接结构的载荷输入提供依据。

2）通过建立气浮轴承结构静力学模型，得到球面母线节点和截面圆节点在不同受力状态下的节点位移，体现了半球形貌变化。

3）在有限元分析基础上改进气浮轴承锁紧螺母结构，改进后的半球沿圆周变形更加均匀，螺母预紧力对半球圆度影响减小，装配应变分布更加合理。