低开关频率下基于MRAS的永磁同步电机无位置传感器控制延时分析

翁 聪，周明磊，游小杰，郝瑞祥

（北京交通大学电气工程学院，北京 100044）

0 引言

永磁同步电机（Permanent Magnet Synchronous Motor，PMSM）具有功率密度大、运行效率高、控制性能好等优点，在轨道交通、航空航天、伺服控制等领域得到了广泛应用。永磁同步电机的控制需要获得可靠的转子位置信息，现多采用霍尔传感器、光电编码器、旋转变压器等机械式传感器，增加了硬件成本及后期维护成本，降低了系统的可靠性。因此，永磁同步电机无位置传感器控制的研究受到了国内外学者的广泛关注。目前，常用的无位置传感器控制方法分为零低速范围内无位置传感器控制方法和中高速范围内无位置传感器控制方法两类。其中，零低速范围内常用的方法有：高频旋转电压信号注入法[1]、高频脉振电压信号注入法[2]和载波频率成分法[3]等；中高速范围内常用的方法有：模型参考自适应法[4]、扩展Kalman滤波器法[5]和滑模观测器法[6]等。模型参考自适应法具有算法简单、鲁棒性强、参数估计易收敛、稳态性能优良等特点，在无传感器控制领域得到了广泛应用。

永磁同步电机无位置传感器控制的关键是能够准确辨识出永磁同步电机的转子位置，然而数字控制中因为各种原因引起的系统延时将导致电机实际发出电压的相位与期望相位之间存在偏差，该偏差会导致永磁同步电机转子位置估算误差增大，降低无位置传感器控制性能。

针对数字控制中的延时问题，国内外学者已经有了许多研究。文献[7]、文献[8]在传统采样模式的基础上，通过提高采样率来减少采样延时。文献[9]从理论上分析了延时对电流PI调节器带宽的影响，并提出了改进的电流采样方法。文献[10]提出了一种新的电流环时序，通过限制电压输出能力来消除计算延时。文献[11]设计了一种改进型离散电流控制器，可以对延时进行补偿。文献[12]分析了延时对交流传动控制系统稳定性的影响，提出了一种基于q轴电流误差的延时补偿方法。

当前，永磁同步电机无位置传感器控制虽然是研究热点，但是针对大功率永磁同步电机双频计算控制框架下的延时分析还较少。本文针对大功率永磁同步电机无位置传感器控制延时问题进行了具体分析，确定了大功率永磁同步电机无位置传感器控制中延时的具体大小，并且根据分析对延时进行了直接补偿。

1 基于MRAS的PMSM无位置传感器控制

1.1 PMSM的数学模型

本文的研究对象是一台内置式永磁同步电机，在同步旋转坐标系下，其定子电压方程为

定子磁链方程为

电磁转矩方程为

机械运动方程为

式（1）～式（4）中， ud、 uq分别为定子电压d轴、q轴的分量，id、iq分别为定子电流d轴、q轴的分量，Rs为定子电阻，ψd、ψq分别为定子磁链 d轴、q轴的分量，Ld、Lq分别为d轴、q轴的电感，Te为电磁转矩，np为电机极对数，ψf为永磁体磁链，J为转动惯量，ωr为电角速度，ωm为机械角速度，B为阻尼系数，TL为负载转矩。

1.2 基于MRAS的PMSM无位置传感器控制策略

在MRAS中，常以永磁同步电机定子电流方程或者磁链方程为参考模型。本文采用定子电流方程为参考模型，永磁同步电机在同步旋转坐标系下以定子电流作为状态变量的状态方程为

式（5）即为参考模型，根据式（5）可以建立对应的可调模型，然后根据参考模型和可调模型设计合适的自适应律（详细推导可参考文献[4]），最后基于Popov超稳定性理论确定自适应律为

转子位置可通过对转速进行积分得到

于是得到了基于定子电流的MRAS转子位置估算系统框图，如图1所示。

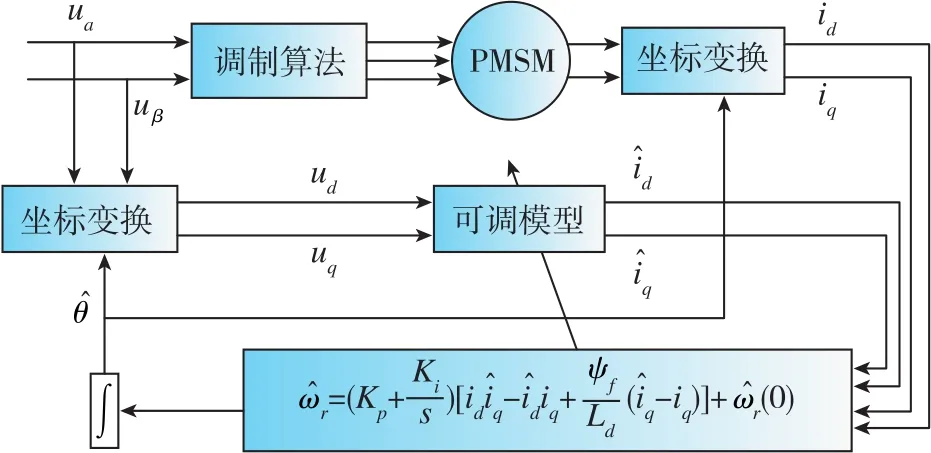
图1 基于MRAS的PMSM转子位置估算框图Fig.1 Block diagram of PMSM rotor position estimation based on MRAS

2 大功率系统控制框架

在小功率系统中，因为其逆变器开关频率很高，在全速度范围内的载波比都可以保持在很高的水平，因此采用一种调制方法即可。而在大功率系统中，由于其电压高、电流大的特点，其逆变器开关频率最大为几百赫兹，从而在中高速范围内载波比维持在一个较低的水平，造成基波电压误差增大、相位延时和谐波增多等问题。因此，在大功率传动系统中通常采用多模式调制策略。

本文采用的多模式调制策略如图2所示，为了与逆变器开关频率对应，电机转速单位用赫兹表示。调制策略分为高载波比下的调制策略和低载波比下的调制策略两个部分，即：在电机转速低于20Hz的高载波比范围内采用异步调制策略，此时调制频率为300Hz；在电机转速高于20Hz的低载波比范围内采用同步调制策略，此时调制频率随着电机转速的变化而变化。

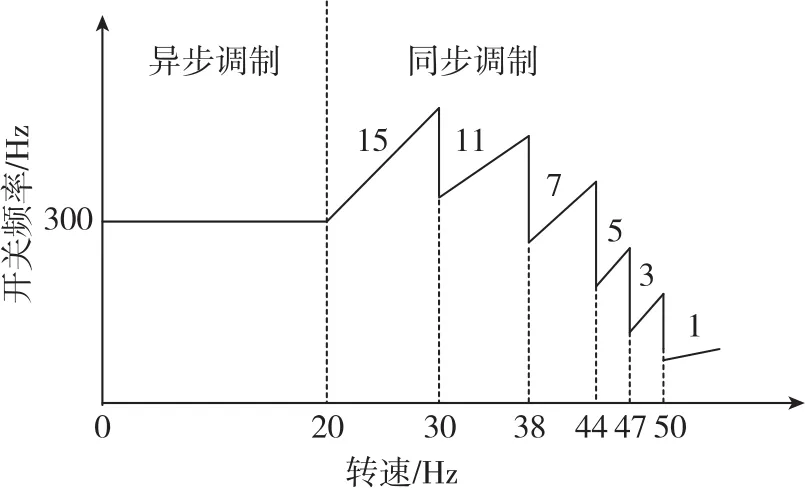
图2 多模式调制策略示意图Fig.2 Schematic diagram of multimode modulation strategy

由于调制部分计算频率不固定，控制部分计算频率固定不变，本文采用控制部分和调制部分分开的控制框架，如图3所示。控制部分计算频率固定为10kHz，电机进入方波工况前采用传统矢量控制方案；进入方波工况后，由于输出电压不可调节，传统的矢量控制方案失效，此时采用改进型矢量控制方案。控制部分和调制部分通过相角调节器连接。

图3 大功率永磁同步电机控制框图Fig.3 Control block diagram of high-power PMSM

相角调节器的结构原理图如图4所示。控制部分发出的转子位置角θc减去调制部分上一拍坐标变换所用的电压矢量角，差值通入P调节器，再将调节器输出叠加到控制部分发出的电机转速fr上，修正后的频率信号通过调制算法中的积分器可以得到调制部分坐标变换所需的电压矢量角θmod。

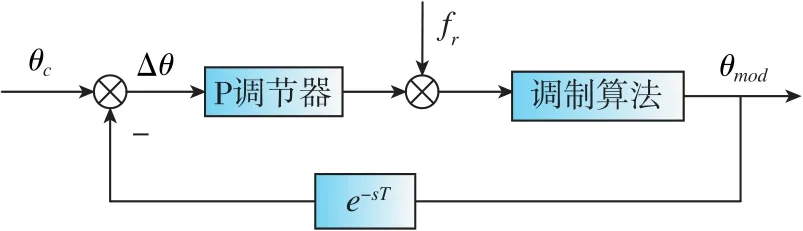
图4 相角调节器结构原理图Fig.4 Structure schematic diagram of phase angle regulator

3 延时分析

3.1 典型数字控制时序延时分析

在数字控制系统中，DSP计算延时和PWM输出延时在系统延时中占据主导地位。

在小功率系统中，典型的电流采样和PWM更新时序图如图5所示，包括采样、计算、PWM更新和PWM输出。图5中，Ts为调制周期，Tc为计算延时，Tpwm为PWM输出延时，Td为系统延时。在实际系统中，采样和计算所用的时间可以忽略不计。

图5 小功率系统中的电流采样和PWM更新时序图Fig.5 Sequence diagram of current sampling and PWM update in low-power system

计算延时即采样时刻到PWM更新时刻的一个调制周期，有

文献[13]推导出了PWM更新作用到系统上的延时为半个调制周期，即更新后的PWM等效在半个采样周期后输出。因此，PWM输出延时为

故在典型数字控制系统中，总的系统延时为

3.2 大功率系统延时分析

在大功率系统中，由于其逆变器开关频率低，因此采用多模式调制策略。此时，为了准确发出指令电压矢量，通常在控制部分与调制部分之间加入相角调节器，使调制部分坐标变换所用的电压矢量角θmod能够跟踪上控制部分发出的转子位置角θc。 由于转子位置角可以由电机转速积分得到，故图4的相角调节器结构原理图可以转化为图6所示的结构原理图。

图6 转化后的相角调节器结构原理图Fig.6 Structure schematic diagram of phase angle regulator after conversion

根据图6所示的相角调节器结构，可以得到

故当PMSM转速稳定不变时，图6所示的系统稳态误差为0，即调制部分坐标变换所用的电压矢量角能够无静差地跟踪上控制部分发出的转子位置角。

大功率系统中的电流采样和PWM更新时序图如图7所示，从电流采样到PWM更新之间存在控制延时Tk和计算延时Tc。 由于调制频率为几百赫兹，而采样频率为几千赫兹，故一个调制周期内进行多次电流采样，PWM更新采用最近一次电流采样计算结果。由于采样频率相较于调制频率很高，控制延时Tk可以忽略不计，计算延时Tc可视为一个调制周期Ts。在不考虑相角调节器的作用时， 存在θmod（k）=θc（k）。 但是在大功率系统中由于相角调节器的相位跟踪作用，调制部分坐标变换所用的电压矢量角θmod（k+1）等于kTs时刻控制部分发给调制部分的转子位置角θc（k）， 即控制部分超前给调制部分发出转子位置角。因此，相角调节器的存在相当于补偿了PWM计算到PWM更新时刻之间一个调制周期的计算延时。更新后的PWM脉冲信号等效在0.5Ts+（k+1）Ts发出PWM信号，即PWM输出存在的0.5Ts延时。故低开关频率下，由于相角调节器的相位跟踪作用，总的系统延时为

图7 大功率系统中的电流采样和PWM更新时序图Fig.7 Sequence diagram of current sampling and PWM update in high-power system

低开关频率下，在异步调制区域内，开关频率不变，随着电机转速升高，延时导致的滞后角度增大。此时，滞后角度为

在同步调制区域内，开关频率和转速都发生变化，但同步调制中调制每次增加的角度固定。本文采用的同步调制方式为每次增加10°，此时的滞后角度为

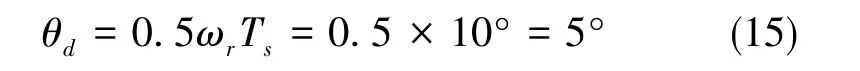
本文采用直接补偿法，即在无位置传感器估算出的转子位置角的基础上加上延时所导致的滞后角度 0.5ωrTs， 以此作为期望发出的电压矢量角。

经过延时补偿后的大功率永磁同步电机控制框图如图8所示。

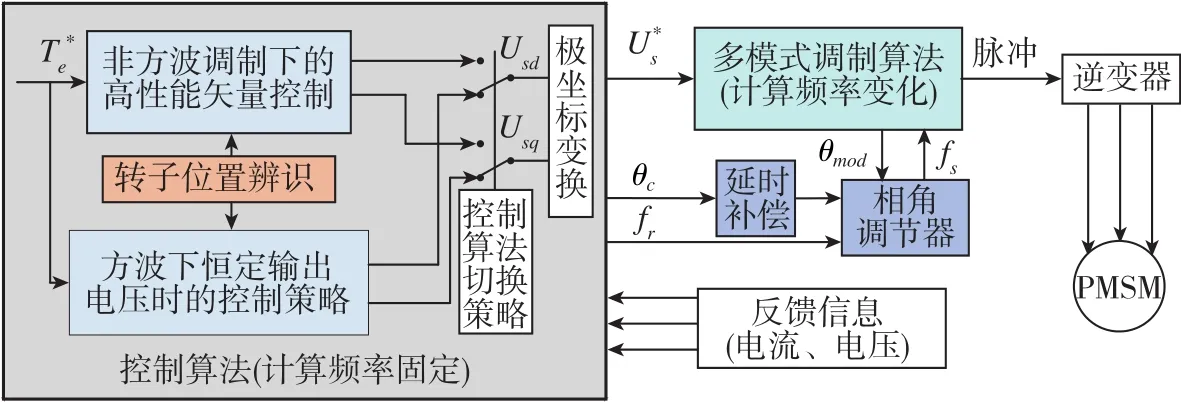
图8 含有延时补偿的大功率永磁同步电机控制框图Fig.8 Control block diagram of high-power PMSM with time-delay compensation

4 仿真分析

4.1 延时分析仿真条件

为了验证前面的理论分析结果，采用Matlab／Simulink软件对本文所研究的基于MRAS的转子位置估算方法进行仿真验证，仿真用电机参数如表1所示。低开关频率下采用多模式调制策略，即：中低速段采用异步调制、中高速段采用同步调制，分别分析异步调制区域内和同步调制区域内系统延时对基于MRAS的转子位置观测的影响。

表1 电机参数Table 1 Parameters of motor

4.2 延时补偿前的仿真验证

（1）异步调制区域内

仿真工况为：低开关频率下，控制频率为10kHz，开关频率为300Hz，转矩指令值为10N·m，电机分别稳定在10Hz、15Hz下运行，仿真结果如图9所示。

图9 异步调制区域延时补偿前的仿真结果Fig.9 Simulation results before time-delay compensation in asynchronous modulation area

由图9（b）可知，在异步调制区域内，随着电机转速的升高，实际逆变器发出的电压矢量滞后期望方向的角度增大，导致电机转子位置估算误差增大。按照3.2节的分析，可以得到以下结论：

当电机转速为10Hz时，此时的转子位置误差为

当电机转速上升到15Hz时，此时的转子位置误差为

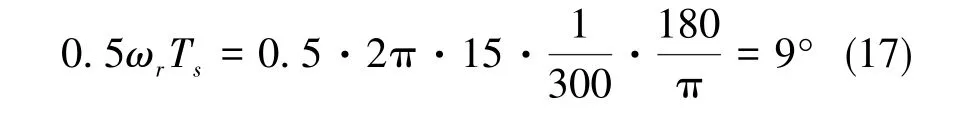
图9（b）中，当转速为10Hz时，转子位置估算误差为6°左右；当转速为15Hz时，转子位置估算误差为9°左右，仿真结果与3.2节的分析一致。

（2）同步调制区域内

仿真工况为：低开关频率下，控制频率为10kHz，开关频率随转速变化而变化，转矩指令值为10N·m， 电机分别稳定在 25Hz、 35Hz、 40Hz、45Hz、50Hz、55Hz下运行，仿真结果如图10所示。

图10 同步调制区域延时补偿前的仿真结果Fig.10 Simulation results before time-delay compensation in synchronous modulation area

由图10（b）可知，在同步调制区域内，转子位置观测误差都在5°附近，仿真结果与3.2节的分析一致。

综上所述，在大功率系统中，不管是在异步调制区域还是在同步调制区域，仿真结果都验证了3.2节中大功率系统延时分析的准确性。由于延时的影响，转子位置误差最大可超过10°。为了提高永磁同步电机无位置传感器控制的性能，有必要对系统延时进行补偿。

4.3 延时补偿后的仿真验证

对3.2节中提出的延时补偿方法进行仿真验证，在控制部分传递给调制部分的电压矢量角度的基础上加上0.5ωrTs的延时补偿，延时补偿后进行仿真。

（1）异步调制区域内

仿真工况为：低开关频率下，控制频率为10kHz，开关频率为300Hz，转矩指令值为10N·m，电机分别稳定在10Hz、15Hz下运行，仿真结果如图11所示。

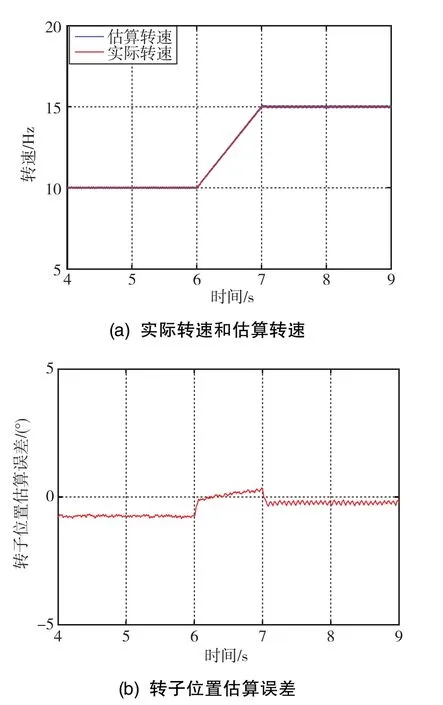
图11 异步调制区域延时补偿后的仿真结果Fig.11 Simulation results after time-delay compensation in asynchronous modulation area

由图11（b）可知，在异步调制区域内，经过延时补偿后，转子位置观测误差都在0°附近，转子位置观测精度显著提高。

（2）同步调制区域内

仿真工况为：低开关频率下，控制频率为10kHz，开关频率随转速变化而变化，转矩指令值为10N·m， 电机分别稳定在 25Hz、 35Hz、 40Hz、45Hz、50Hz、55Hz下运行，仿真结果如图12所示。

图12 同步调制区域延时补偿后的仿真结果Fig.12 Simulation results after time-delay compensation in synchronous modulation area

由图12（b）可知，在同步调制区域内，经过延时补偿后，转子位置观测误差都在0°附近，转子位置观测精度显著提高。

综上所述，不管是在异步调制区域还是在同步调制区域，经过延时补偿后，基于 MRAS的PMSM转子位置观测精度显著提高，仿真结果验证了3.2节中提出的直接延时补偿方法的有效性。

5 结论

本文针对大功率永磁同步电机无位置传感器控制系统延时进行研究，分析了大功率永磁同步电机双频计算控制框架下相角调节器在系统延时中的补偿作用，确定了低开关频率下系统延时的具体大小，并且根据理论分析进行延时补偿，仿真结果验证了本文关于大功率系统中延时分析的准确性。仿真结果显示，经过延时补偿后，在全速度范围内，基于MRAS的永磁同步电机转子位置观测误差都在0°附近，转子位置观测精度显著提高。