微机电系统陀螺仪单层隔热槽结构优化设计

张 浩，何汉辉，肖定邦，曾承志，吴学忠

（1.国防科技大学智能科学学院，长沙 410073；2.唐智科技湖南发展有限公司，长沙 410007）

0 引言

微机电系统（Micro Electro Mechanical Systems，MEMS）陀螺仪是一种角速度传感器，具有体积小、质量小、成本低、功耗低等优点[1]。随着智能无人系统、微型卫星、制导弹药等领域的发展，国防现代化的需要对高性能的微机电系统陀螺仪提出了迫切需求。目前，典型的高性能微机电系统陀螺仪按照结构形式可分为四质量块式、环形及嵌套环式、微半球式等。其中，环形陀螺是平面全对称结构，加工鲁棒性好，性能潜力较高，采用成熟的平面加工工艺，可批量化加工，制造成本更低，是目前最具潜力的微机电系统陀螺仪方案之一[2]。同时，环形微机电系统陀螺仪的性能受到了加工工艺、结构设计等多种因素的限制。

提高微机电系统陀螺仪的性能，很重要的一点是要提高陀螺谐振子的品质因数（Q值），Q值是衡量每个振荡周期谐振器能量损失的指标。微机电系统陀螺仪中存在不同的能量损耗机制，包括热弹性阻尼、空气阻尼、支撑损耗和表面损耗等。对于真空封装的硅基环形陀螺仪来说，热弹性阻尼是其主要的损耗机制[3]。对微机械谐振器热弹性阻尼的研究引起学者们的极大关注。Zener[4]最早建立了热弹性阻尼的理论模型，考虑了梁的弯曲厚度方向的热流动。Lifshitz等[5]对Zener模型进行了改进，采用了复杂的温度场，并给出了矩形截面梁谐振器的热弹性阻尼的具体表达式。Wong等[6]基于Zener模型提出了具有矩形截面的环形谐振结构面内弯曲模态的热弹性阻尼解析解。

为了提高微机电系统陀螺仪的理论品质因数，通常采用优化谐振结构几何形状以及尺寸的方法以减小热弹性阻尼。Candler等[7]通过实验发现：在谐振梁结构中开槽会影响热弹性品质因数，开槽的作用是扰乱横跨梁的热流，从而改变能量耗散的过程。研究表明，开槽可以获得比Zener理论预测的更高的品质因数，但在高频条件下，开槽也可能使品质因数减小。Hossain等[8]通过有限元方法研究了高Q值环形谐振器的热弹性阻尼机制，考虑了环的尺寸以及支撑梁的尺寸形状对热弹性阻尼的影响，最后对环上挖隔热槽的影响也进行了研究。结果表明，隔热槽对于Q值较低的谐振器能够提高Q值，但对于高Q值谐振器可能会降低Q值，并且没有研究槽的具体尺寸参数和分布方式对Q值的影响。

本文在环形微机电系统陀螺仪的外环上添加隔热槽结构，对环形微机电系统陀螺仪隔热槽参数进行了优化设计，利用有限元分析软件COMSOL Multiphysics对陀螺仪的谐振频率、热弹性品质因数进行了仿真分析，并利用仿真结果计算了陀螺仪的等效质量、机械热噪声等性能参数，从而对槽的大小、数量、位置等变化对陀螺仪性能参数的影响规律进行研究，以指导隔热槽结构的优化设计，得到性能提升的环形微机电系统陀螺仪。

1 热弹性阻尼

热弹性阻尼广泛存在于弹性固体结构发生谐振时。当谐振结构变形时，固体的应力场与温度场产生耦合，即固体的机械模态与热力学模态发生耦合，压缩变形的区域温度较高，拉伸变形的区域温度较低，从而产生温度梯度，热量从高温区域向低温区域进行传导，导致部分机械能以热量的形式耗散，这种过程被称为热弹性弛豫。对于横截面为矩形的Euler-Bernoulli梁，只考虑结构振动方向的一维热流动，则结构的热传导方程为[9]

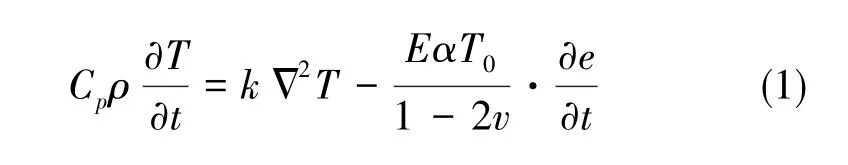
式（1）中，Cp为材料的比热，ρ为密度，E为杨氏模量，α为热膨胀系数，T0为梁的平衡温度，k为热传导率，υ为泊松比，e为结构的体应变，Δ为Laplacian算子。

对于横截面为矩形的Euler-Bernoulli梁，结构发生弯曲振动时的运动方程可表示为[6]

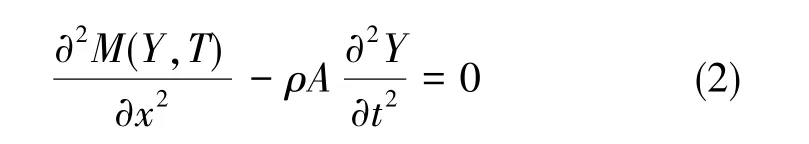
式（2）中，A为横截面积， M（Y， T）为结构受到的弯矩。除了通常的弹性弯矩外，还包括了梁截面温度分布影响的热弹性弯矩。对于弯曲变形且横截面为矩形的梁而言，几乎所有弛豫发生在弯曲方向，98.6%的热弛豫通过主热力学模态实现[4]。只考虑主热力学模态的热弛豫，根据热边界条件联立式（1）和式（2）可解得梁的热弹性阻尼为

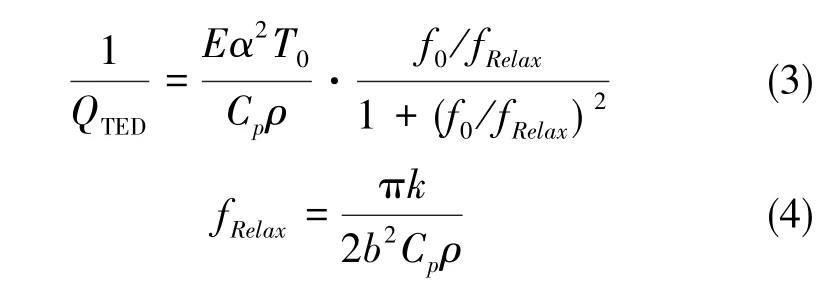
式（3）中，QTED为热弹性品质因数，f0为谐振频率，fRelax为热弛豫频率，f0／fRelax称为归一化频率。式（4）中，b为发生热流的梁的厚度。当梁上有隔热槽时，梁上的热传导不连续，振动产生的热流被隔热槽所扰乱，振动时机械模态与不同频率的热力学模态相互耦合，减少了与主热力学模态的耦合，导致热弹性阻尼的变化，从而影响谐振梁的品质因数。对于环形结构的面内弯曲模态来说，上述分析方法同样可以用于其热弹性阻尼的分析[6]，但理论计算方法无法得到结构中的热量分布情况，且对于复杂结构，一维模型的计算误差较大，需要进一步拓展为三维热弹性阻尼模型。因此，为得到更为准确的热弹性阻尼值及热量分布，本文采用有限元仿真方法对带有隔热槽的环形结构进行热弹性阻尼分析。

2 微机电系统陀螺仪的基本结构和性能参数

2.1 工作原理与基本结构

本文研究的环形微机电系统陀螺仪是一种平面全对称的振动式陀螺仪，其工作原理是利用哥氏力效应实现对角速度的检测，激励和检测方式通常采用静电激励和电容检测。当陀螺受到外界激励时，谐振结构被激发出驱动模态，在驱动方向面内保持恒幅振动，波峰处环内侧被压缩，温度升高，环外侧被拉伸，温度降低，热流方向由壁厚方向向外；而波谷处则相反，热流方向由外向内。当角速度输入时，谐振结构上所有运动微元均受到哥氏力作用，从而激发出检测模态，检测模态与驱动模态为同一阶模态的简并模态。检测模态振动的幅值与输入角速度的大小成正比，通过检测其振幅即可算出角速度的大小。

本文研究的隔热槽结构微机电系统陀螺仪由中间支撑锚点、外环以及锚点和外环之间的8对谐振梁组成，工作在椭圆简并模态，驱动模态与检测模态之间的角度为45°，其基本结构及工作模态示意图如图1所示。隔热槽结构设置在外环上，贯穿了整个结构，为了使驱动模态和检测模态频率裂解最小，整体结构应当满足1／8对称的条件[10]。因此，槽在外环上均匀分布，且数量应当为8的倍数。

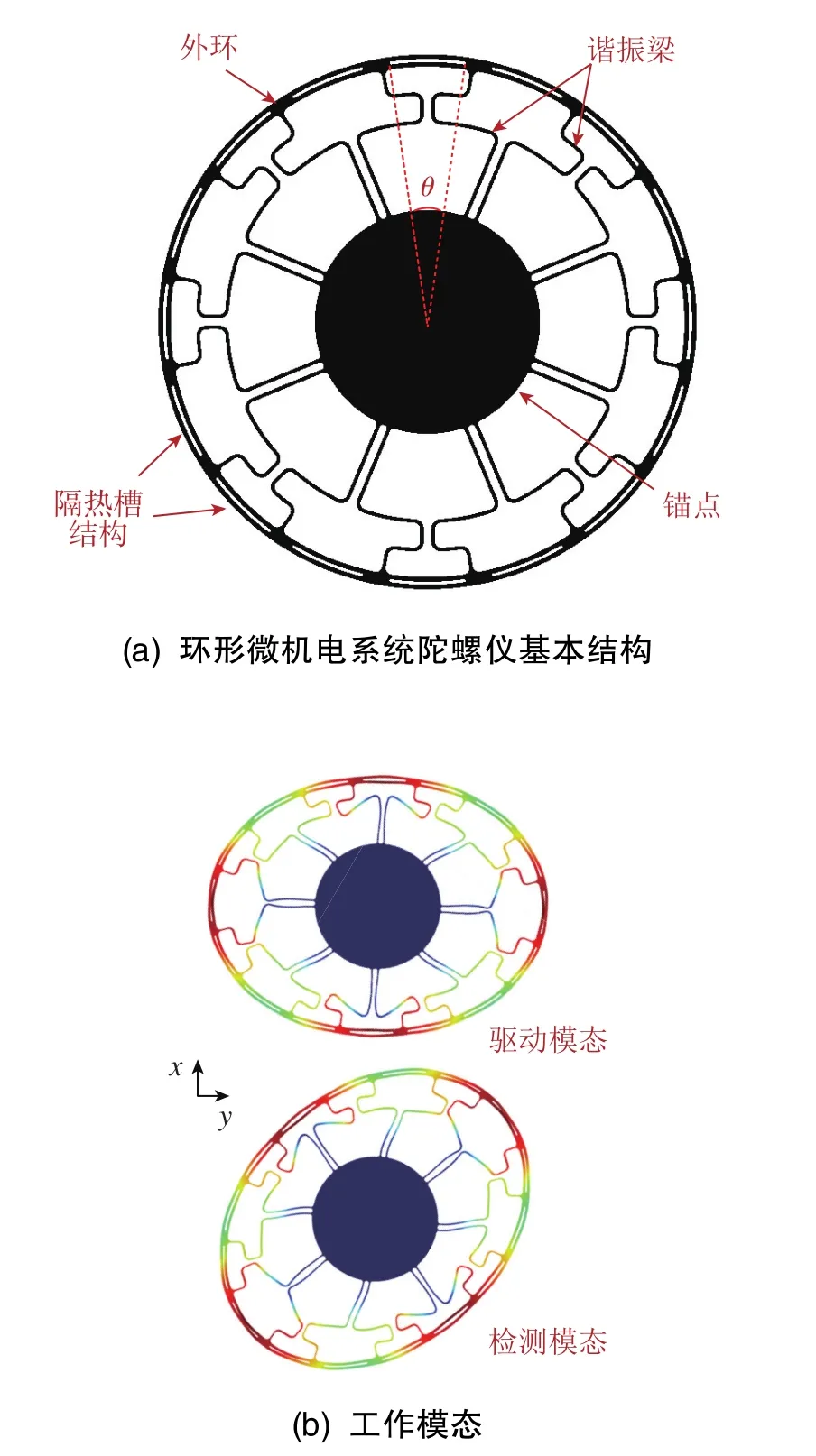
图1 环形微机电系统陀螺仪的基本结构和工作模Fig.1 Basic structure and operating mode of the ring MEMS gyroscope

2.2 微机电系统陀螺仪的性能参数

在进行结构设计时，除了谐振频率f0和Q值以外，陀螺仪的等效质量meff和谐振结构本身的机械热噪声Ωmech也是关键参数。固体波动陀螺的等效质量与工作模态的振型有关，环形微机电系统陀螺仪属于固体波动陀螺，其等效质量meff和机械热噪声Ωmech的计算公式如下[11-12]

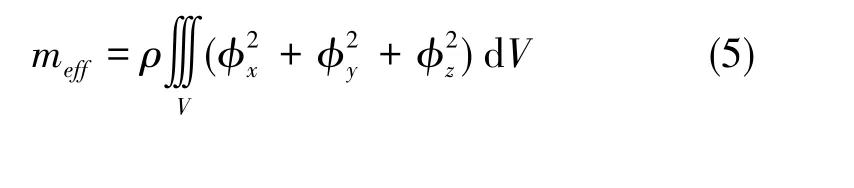
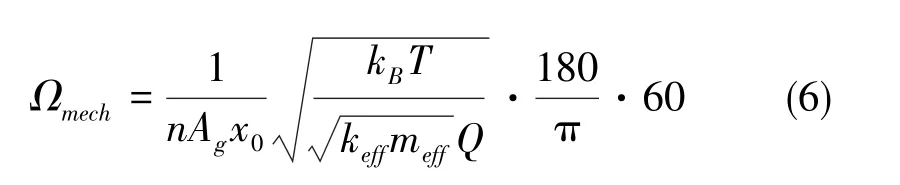
式（5）中，ϕx、ϕy、ϕz为 Descartes坐标表示的振型函数，它们可以由COMSOL模态分析仿真结果处理得到[10]。式（6）中，kB为Boltzmann常数，T为陀螺仪的工作温度，n为陀螺仪的振动模态阶次，Ag为陀螺仪的角度增益，这几个参数无法在结构设计中进行优化；keff为等效刚度；x0为振动位移，此参数由后期陀螺仪的测控电路进行控制，暂时定为x0=2μm。由式（6）可知，陀螺仪的机械热噪声主要与Q值、等效刚度keff和等效质量meff有关。隔热槽结构能够提升微机电系统陀螺仪的Q值，但同时也减小了其等效刚度和等效质量，因此在进行结构优化设计的同时，需要权衡Q值与等效质量和机械热噪声之间的关系。

2.3 仿真参数及有效性验证

本次仿真采用的软件为有限元仿真软件COMSOL Multiphysics，仿真步骤如下：首先利用Solidworks建立参数化模型，利用 COMSOL软件的livelink for Solidworks接口将模型导入COMSOL中，设置材料为（111）晶向单晶硅材料，在锚点处设置固定约束，对整体结构划分网格，利用热弹性模块对环形结构进行特征频率研究，得出其温度分布、模态振型和模态位移，同时计算出其谐振频率和热弹性品质因数。COMSOL软件内置与MATLAB软件的接口，即COMSOL with MATLAB模块，谐振子的等效质量、机械热噪声等参数可以由MATLAB调用COMSOL的仿真数据计算得到。仿真中的材料属性如表1所示。

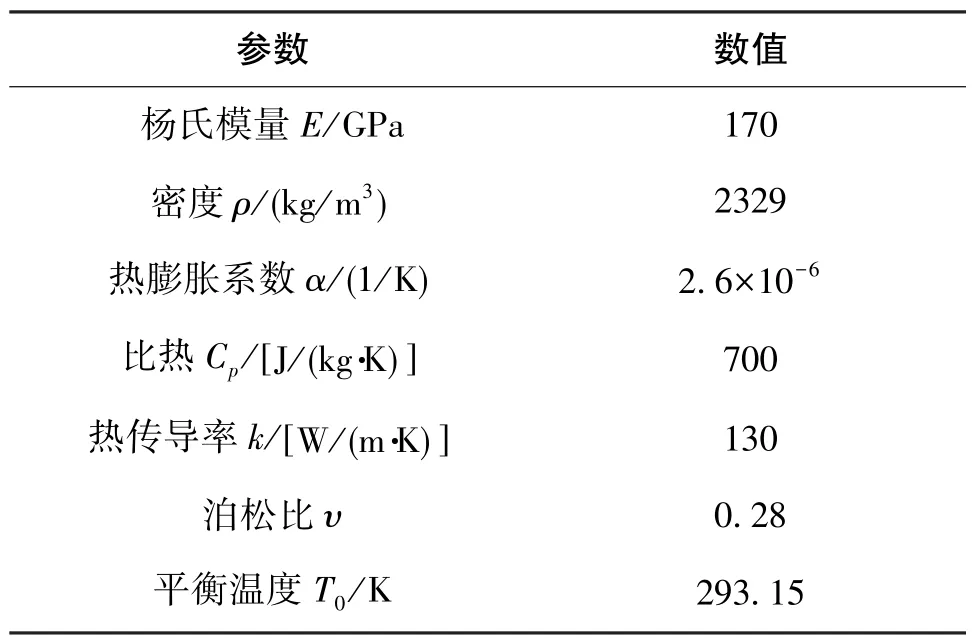
表1 仿真中的材料属性Table 1 Parameters in simulation

为了验证仿真模型的有效性，首先仿真了半径为3mm的谐振环（不含谐振梁）的热弹性品质因数QTED。其中，发生热流动的梁的厚度即环的壁厚b变化区间为40μm～120μm，步长设置为5μm。根据式（3）绘制出热弹性品质因数QTED与归一化频率f0／fRelax的理论关系曲线（Zener曲线），并将仿真数据点与Zener曲线绘制到同一幅图中进行对比，结果如图2所示。

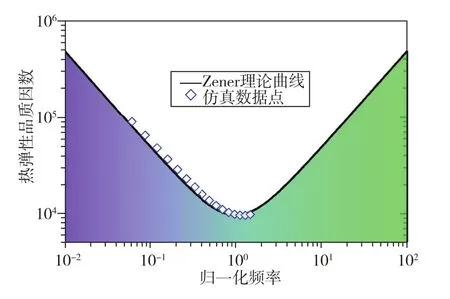
图2 谐振环Zener理论曲线与仿真数据对比Fig.2 Comparison between Zener theoretical curve and simulation data of the resonant ring

由图2可知，仿真谐振环的壁厚b变化得出的QTED数据点与Zener曲线变化趋势拟合较好，验证了仿真模型的准确性。

3 仿真结果与分析

3.1 不含隔热槽结构的仿真结果

主要研究了环形结构外环上隔热槽的位置（离中性面的距离d）、槽宽度w、槽长度（用圆心角θ表示）和槽个数n对陀螺谐振频率f0、热弹性品质因数QTED、等效质量meff和机械热噪声Ωmech的影响规律，进而对隔热槽的参数进行了优化设计，得到了较优的隔热槽参数。

本次仿真采用的环形微机电系统陀螺仪结构的基本参数如表2所示。

表2 环形微机电系统陀螺仪的基本结构参数Table 2 Basic structure parameters of the ring MEMS gyroscope

首先通过仿真计算出不含隔热槽的陀螺仪性能参数，利用COMSOL热弹性模块仿真得到的温度分布如图3所示。可以看出，温度分布主要沿外环壁厚方向，且变形大的地方温度变化也大。

图3 环形微机电系统陀螺仪的温度分布Fig.3 Temperature distribution of the ring MEMS gyroscope

通过仿真结果计算出的陀螺仪主要性能参数汇总如表3所示。

表3 不含隔热槽结构的陀螺仪性能参数Table 3 Performance parameters of the gyroscope without thermal isolation slots

3.2 槽的位置对性能参数的影响规律

为了研究隔热槽在外环上的位置对陀螺仪性能参数的影响，槽被设置在结构外环上，贯穿了整个结构高度，槽长度θ=20°，槽个数n=8，槽在外环圆周上均匀分布，槽宽度w=10μm，改变槽离中性面的距离d，中性面以外用负号表示，中性面以内用正号表示。仿真计算陀螺仪的谐振频率f0、热弹性品质因数QTED、等效质量meff和机械热噪声Ωmech，仿真结果如图4所示。

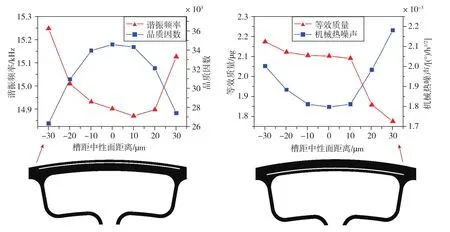
图4 槽的位置对陀螺仪性能的影响规律Fig.4 Influence of slot position on the gyroscope performance

由图4可知，与不含隔热槽的结构相比，在外环上设置隔热槽对陀螺仪的QTED有较大提升，且降低了陀螺仪的Ωmech。 当槽的位置从外向内时，QTED的变化趋势是先增大后减小，在中性面时值最大；f0和Ωmech的变化趋势是先减小后增大，在中性面时Ωmech值最小；而meff则呈下降趋势。综合以上来看，当槽位于中性面位置时，机械热噪声最小，性能提升效果最好。因此，在后续的仿真中，都将槽的位置设置在中性面上。

3.3 槽的长度和个数对性能参数的影响规律

接下来研究槽长度θ和槽个数n对陀螺仪的谐振频率f0、热弹性品质因数QTED、等效质量meff和机械热噪声Ωmech的影响规律。为了使环形陀螺仪工作在椭圆简并模态且驱动模态与检测模态间频率裂解最小，环形陀螺仪的结构应当满足1／8对称的条件，因此将槽个数n分别设置为8、16、24、32、40和48，设置槽宽度w=40μm，槽长度θ从小到大变化，直到槽布满整个外环，仿真结果如图5所示。

由图5可知，在不同的槽个数n条件下，随着槽长度θ的增加，QTED均呈上升趋势，最终将达到极限， 而 meff均呈下降趋势。 由图5（a）～图 5（c）可知，当槽个数n为8、16和24时，随着槽长度θ的增加，Ωmech的变化趋势是先下降后上升，存在一个最小值。 由图5（d）～图5（f）可知， 当槽个数n为32、40、48时，Ωmech呈下降趋势，在单层槽布满整环时，QTED最大、Ωmech最小。由此可见，在槽个数n较少时，槽长度θ对陀螺仪性能的提升效果并不是越长越好；当槽个数n较多时，槽长度θ越长其提升效果越好。

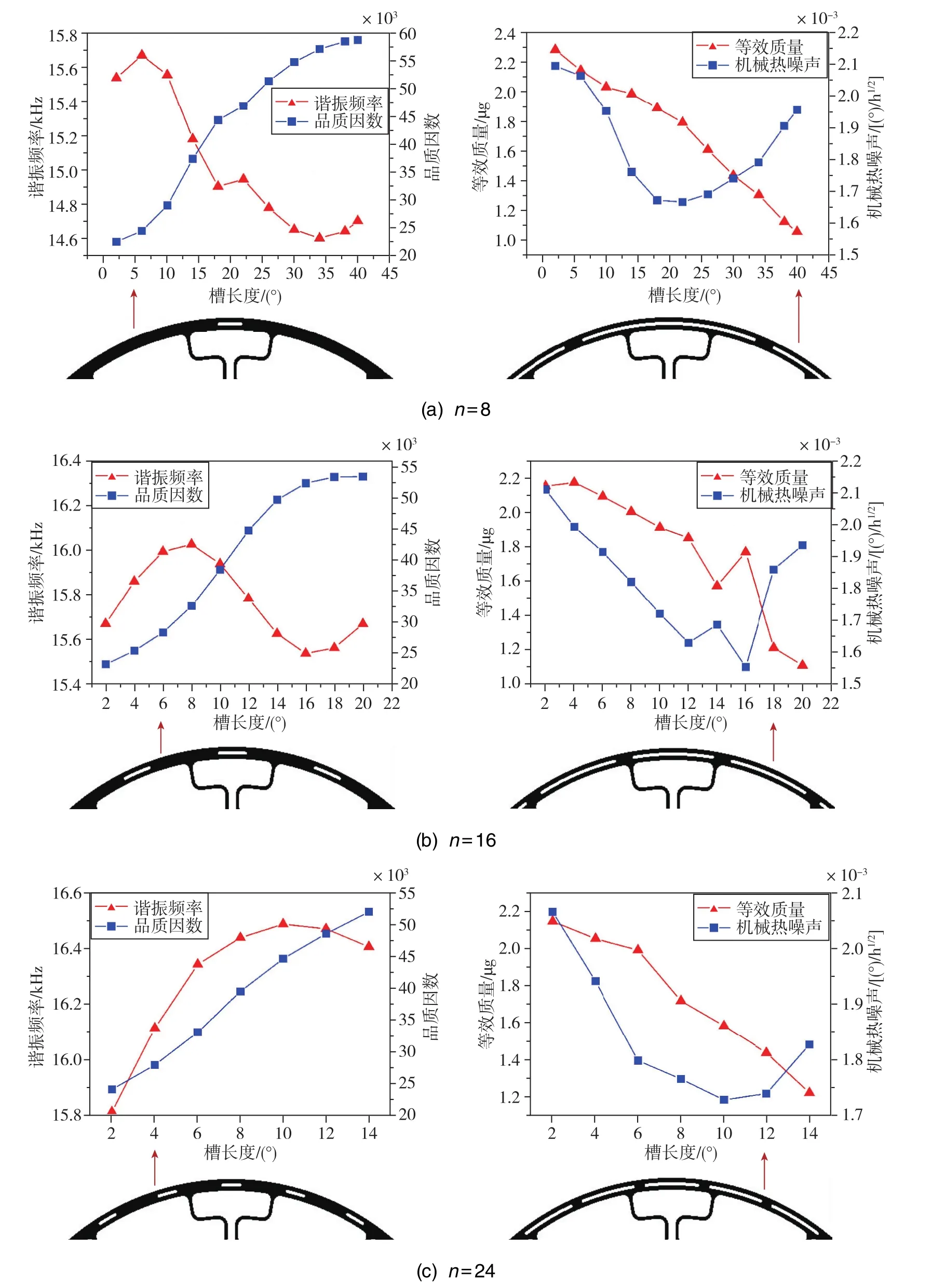
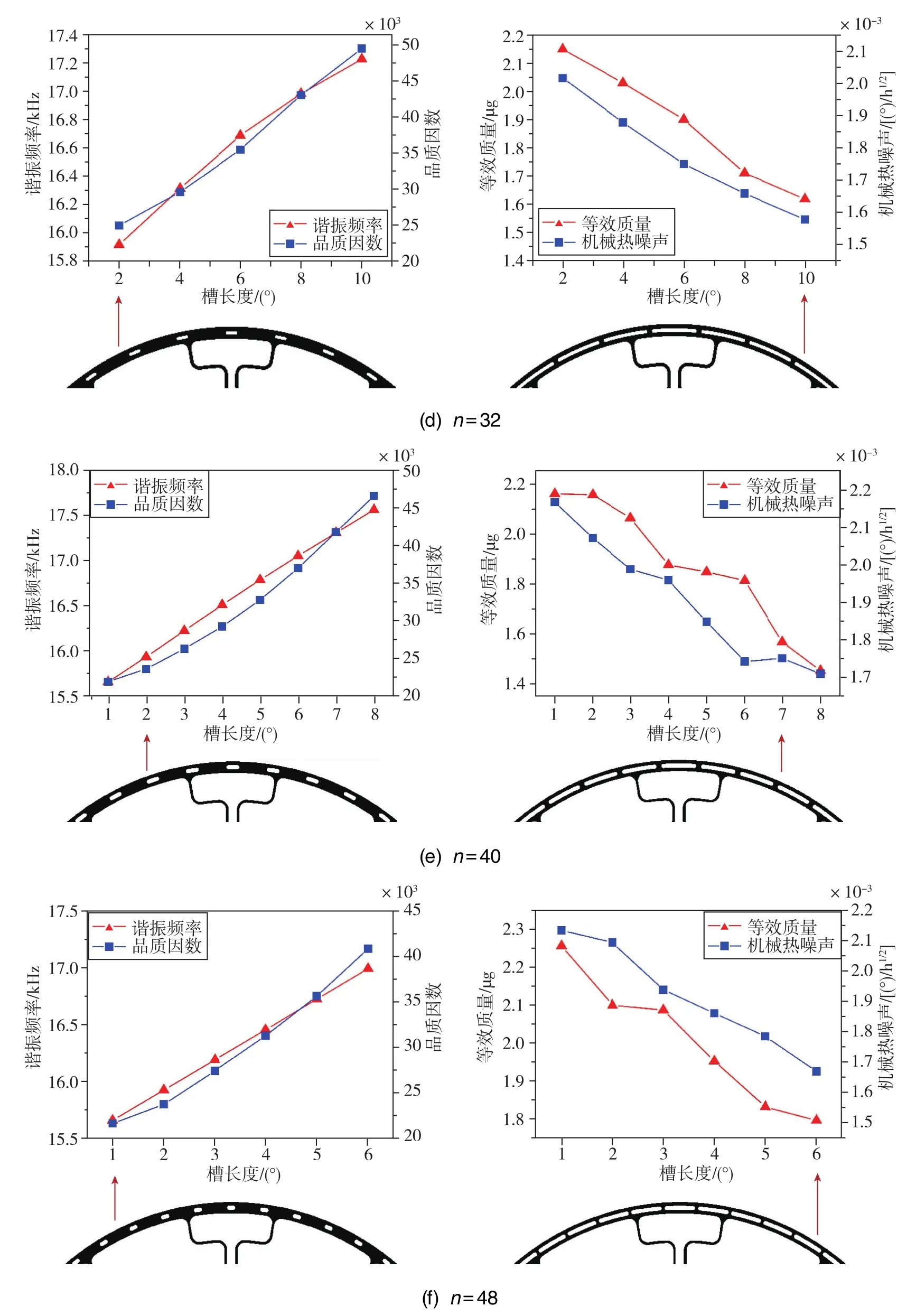
图5 不同槽个数n条件下槽长度对陀螺仪性能的影响规律Fig.5 Influence of slot length on the gyroscope performance with different slot numbers

接下来，将不同槽个数n条件下Ωmech最小的情形进行综合比较，结果汇总如图6所示。

由图6可知，当槽个数n≥32时，对QTED的提升效果小于槽个数较少时，并且Ωmech呈上升趋势。综合来看，当槽个数n=16、槽长度θ=16°时，QTED最大，同时Ωmech最小，此时隔热槽对环形微机电系统陀螺仪的性能提升最大，是较优的选择。

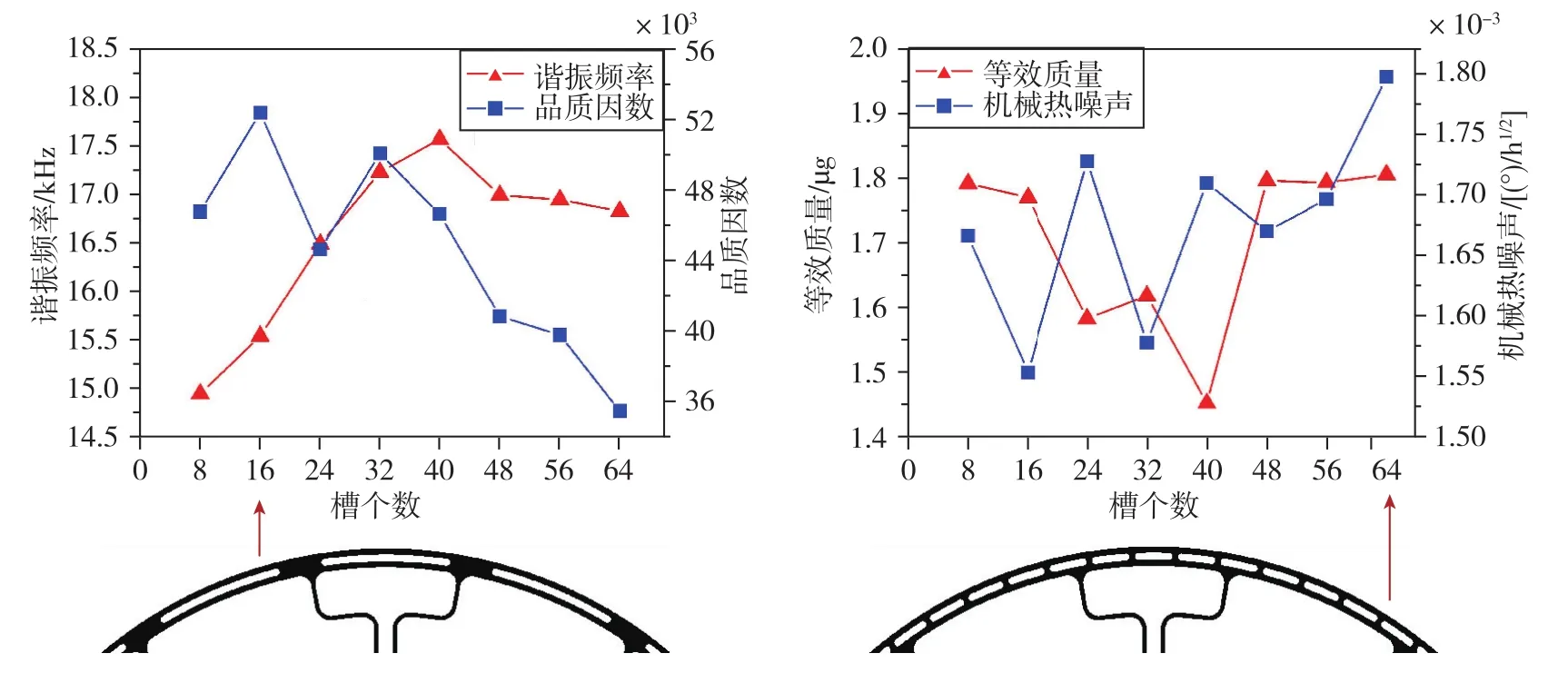
图6 不同槽个数条件下最优性能对比Fig.6 Comparison of optimal performance with different slot numbers

3.4 槽的宽度对性能参数的影响规律

为了分析槽宽度w对性能的影响，在上文研究的基础上，设置槽个数n=16、槽长度θ=16°，仿真计算了槽宽度w从5μm变化到60μm的陀螺仪谐振频率f0、热弹性品质因数QTED、等效质量meff和机械热噪声Ωmech， 仿真结果如图7所示。

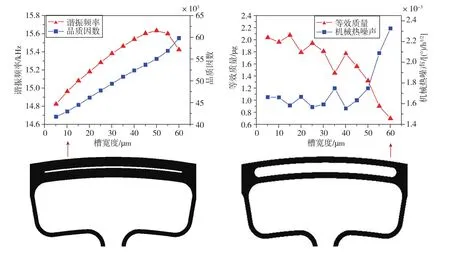
图7 槽宽度对陀螺仪性能的影响规律Fig.7 Influence of slot width on the gyroscope performance

由图7可知，随着槽宽度w的增加，f0先上升后下降，QTED呈上升趋势，当槽宽度w大于40μm时，meff呈下降趋势，Ωmech呈上升趋势。 综合来看，当槽宽度w=40μm时，QTED较大且Ωmech最小，是最优的选择。

综合以上仿真结果，设置单层隔热槽的槽长度θ=16°、槽宽度w=40μm、槽个数n=16，位置设置在外环中间，通过仿真结果计算出的陀螺仪主要性能参数汇总如表4所示。

表4 优化后的陀螺仪主要性能参数Table 4 Performance parameters of the optimized gyroscope

经过单层槽优化后，与不含隔热槽的结构相比，热弹性品质因数QTED提升了139%，同时机械热噪声Ωmech减小了26.9%，综合性能较好。

4 结论

本文通过有限元仿真的方法研究了隔热槽的尺寸以及分布情况对环形微机电系统陀螺仪性能参数的影响规律，并对环形微机电系统陀螺仪单层隔热槽结构进行了优化设计，得出如下结论：1）当单层隔热槽位于环中性面位置时，对品质因数等性能参数的提升最大；2）隔热槽的宽度和长度越大，对品质因数的提升效果越明显，但对等效质量的减少程度较大，在槽个数较少时，槽长度对陀螺仪机械热噪声的提升效果并不是越长越好；3）对于结构尺寸参数已经确定的环形微机电系统陀螺仪，应当根据其特定的尺寸条件进行分析，找到综合性能较优的隔热槽参数。