非均质砂岩储层压汞分形特征与储层评价
2022-01-18冯阵东王光绪梁书义
冯阵东,周 永,吴 伟,王光绪,梁书义,于 静
(1.河南理工大学安全科学与工程学院,河南焦作 454003;2.河南理工大学资源环境学院,河南焦作 454003;3.胜利油田东胜精攻石油开发集团股份有限公司,山东东营 257061)
油气储层的孔隙结构控制着流体的存储和流动等物理特性,是制约油气开采的重要因素,直接影响着储层的产油气能力。油气储层研究的孔隙尺度越来越小,微观孔隙结构具有强烈的非均质、不规则、复杂性等,这种非均质性受到沉积作用、成岩作用、构造应力作用等因素的影响,产生的非均质性差异制约着油气储集、运移等过程,储层非均质性描述是储层评价的重要因素之一。分形几何学为分析复杂储层的孔隙结构提供新的思路和方法[1],能够利用储层微观孔隙自相似性定量评价储层非均质性[2-4]。利用分形几何方法处理压汞数据,进一步进行孔隙结构的复杂性和非均质性评价和分形维数表征,是储层孔隙描述的常用手段[5-9]。目前进行压汞孔隙分形具有多种成熟的数学模型,包括Menger海绵模型[10]、热力学分型模型[11]、Sierpinski地毯模型[12]、毛细管束模型等[13],但是这些模型均未从整体上综合考虑储层孔隙中不同尺度孔隙分形特征的差异[13-14]。Su等[13]考虑致密砂岩孔隙多重分形的特点,提出加权平均的综合分形维数Dsw替代分段分形维数,并与储层物性对比取得较好的对应关系。然而在计算综合分形维数Dsw的模型中,并未考虑分段分形维数值与加权值的地质意义,求取得到的综合分形维数指标在评价储层物性特征时,常存在分形维数值与储层孔隙度、渗透率之间的矛盾。笔者对Dsw模型进行改进后,提出新的综合分形维数Dp,结合珠江口盆地白云凹陷PY35-2-4砂岩和PY35-2-5细砂岩的15组样品压汞曲线分形指标求取,将其与孔隙度、渗透率参数进行对应,验证综合分形指标Dp的合理性,在此基础上利用该指标对储层进行分类评价,取得较好的应用效果。
1 毛细管束模型分形计算原理
毛细管束模型中(图1),任意一条非常不规则的管道长度L是管道半径的函数,满足[15]:
(1)
式中,r为毛细管的半径,μm;L为半径为r的弯曲毛细管的长度,μm;L0为管道起点到终点的直线距离,μm;DT为衡量毛细管弯曲度的分形维数,数值分布在1~3,即毛细管为直线时,分形维数值等于1,弯曲的毛细管在三维空间内任意扭曲,受限与三维模型,故分形维数值DT小于3。
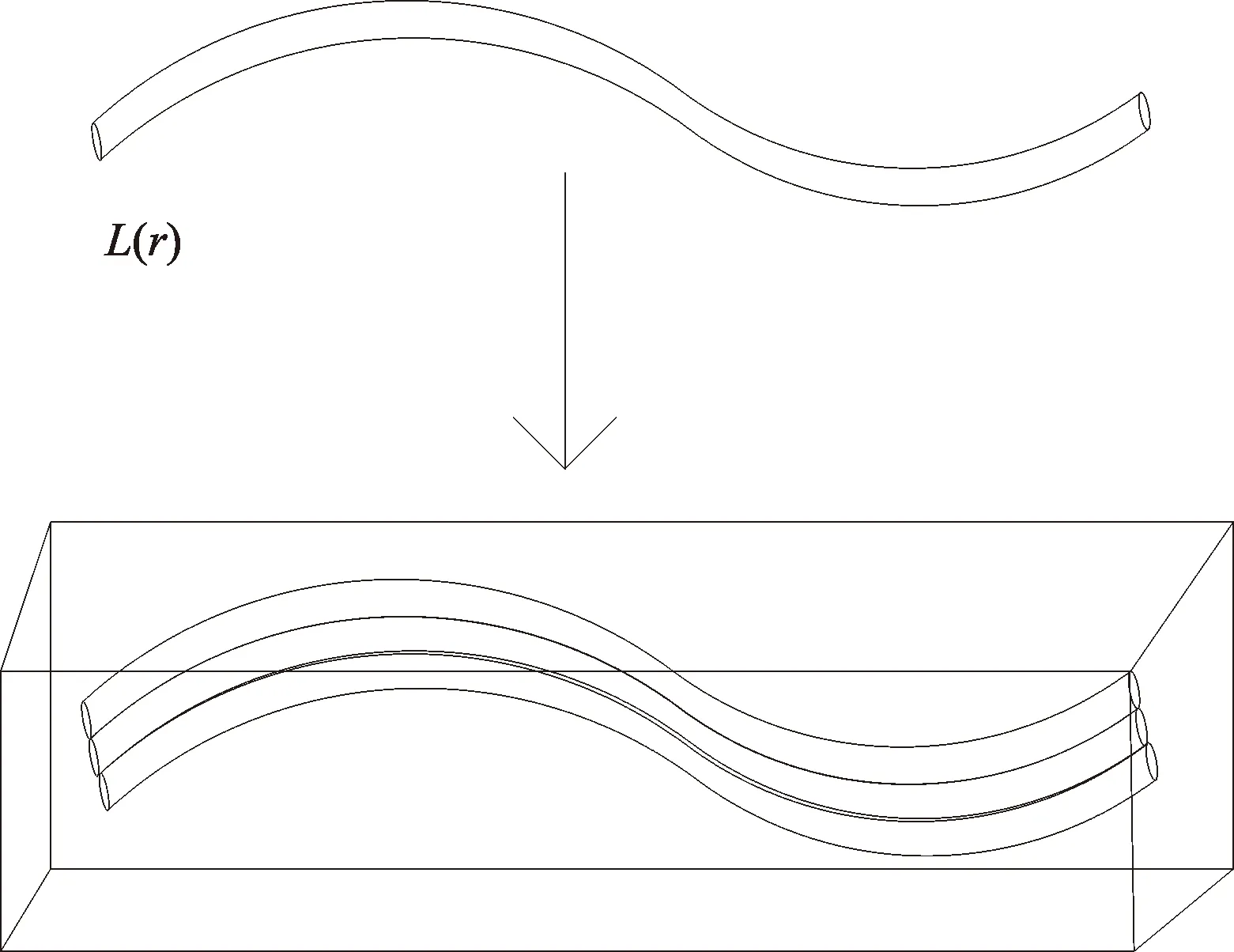
图1 毛细管束填充孔隙示意图Fig.1 Imaginary diagram of capillary bundle filling pores
根据分形理论,在毛细管中当测量尺度为r时,以r为半径的管道数量为N(r),且有如下关系[16]:
N(r)∝r-Df.
(2)
式中,N(r)为半径为r的管道个数;Df为衡量毛细管发育程度的分形维数,代表二维管束截面在三维空间的发育程度,故取值为2~3。从中可知尺度r越小数量N(r)就越大,占据的孔隙空间就越多。当水银进入到孔隙空间时有关系式:
N(r)=VHg/(πr2L).
(3)
式中,VHg为汞流经到半径为r的管道时的累积进汞量,μm3。
由式(1)、(2)和(3)可得:
VHg∝r(3-Df-DT).
(4)
再根据杨-拉普拉斯方程中pc和r成反比[17]有:
(5)
式中,pc为毛细管压力,MPa。该数据可以由压汞数据直接读取,再根据SHg=VHg/Vp,取对数有:
LogSHg=(Df+DT-3)logpc+C.
(6)
式中,SHg为进汞饱和度,由压汞测试直接读出,%;C为常数。
由此可以看出,在双对数坐标中SHg与pc存在线性关系,直线的斜率k满足:
k=Df+DT-3.
(7)
式中,Df为孔隙空间的分形维数;DT为孔隙管道的曲折度分形维数;Df+DT的理论值为3~6,符合分形规律的任意段压汞曲线的分形维数Di都是由Df+DT构成,相应段的分形维数值Di满足:
Di=3+ki.
(8)
式中,Di为第i段压汞曲线对应的分形维数值;ki为双对数坐标系中第i段压汞曲线的斜率。
2 各项分形维数值的计算及地质意义
2.1 相关试验数据的获取
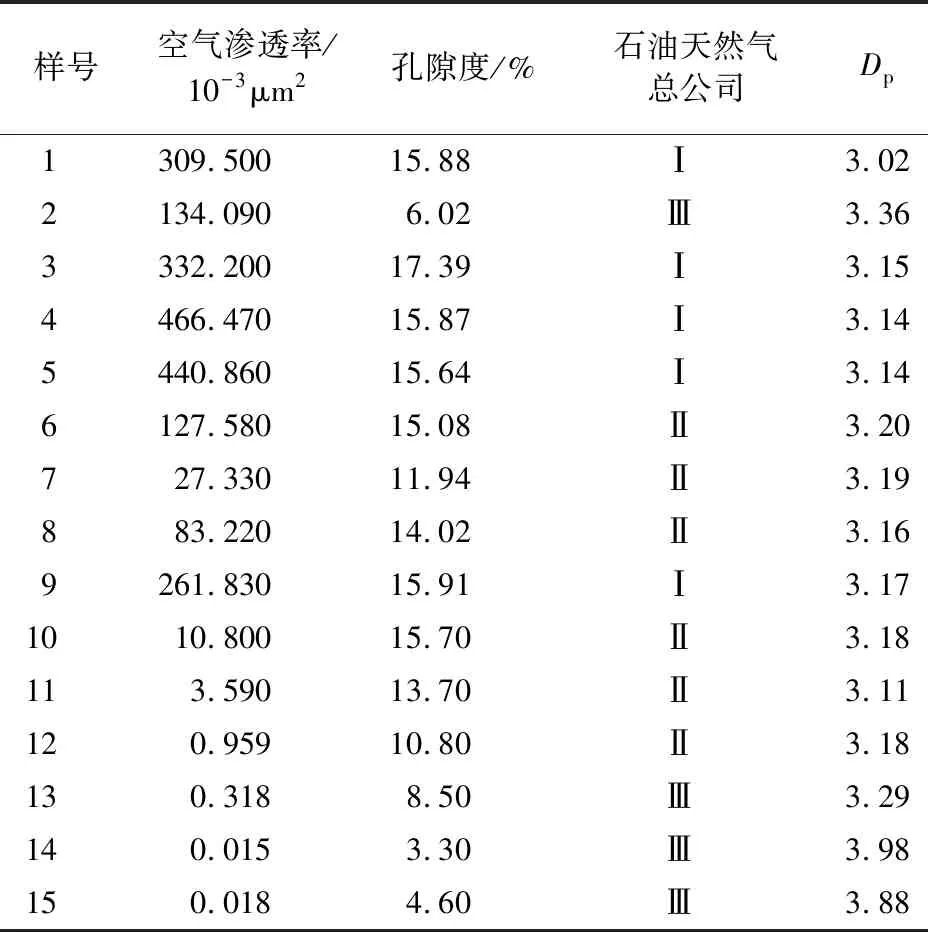
本次试验的15个砂岩样品为取自珠江口盆地白云凹陷PY35井区珠江组底部,在进行压汞分析之前已经进行相关测试并获取样品的储集物性、压汞数据等,具体参数见表1。
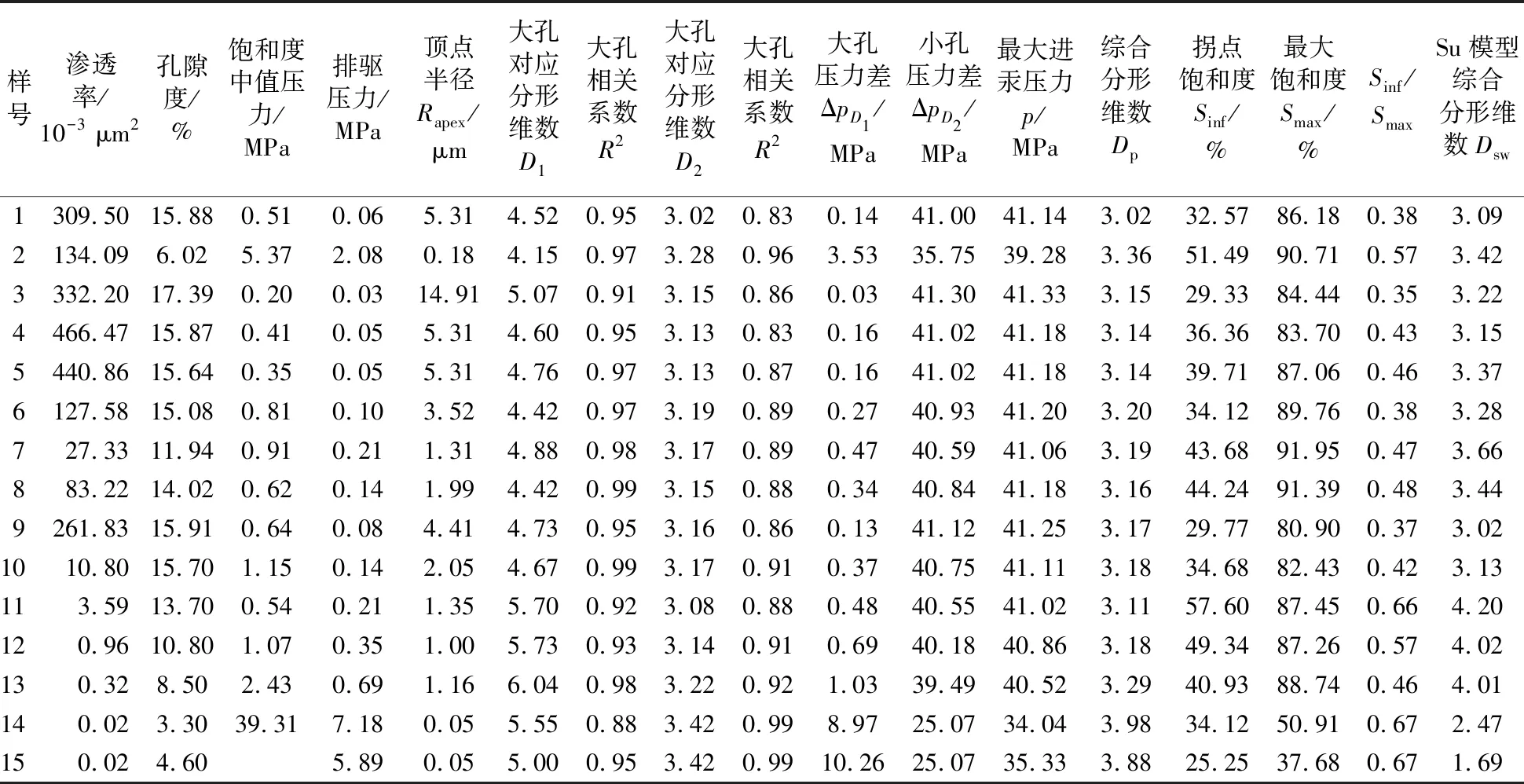
表1 样品统计数据Table 1 Sample statistic data
2.2 分形维数D1和D2计算及地质意义
不同成因类型的储层孔隙分布具有差异性,形成孔隙结构的多层次性、复杂性特征。在进行储层孔隙分形研究时,这种多层次性表现为分段明显的多重分形特征。用于压汞数据分形分析的双对数图版(图2)具有斜率明显不同的两段特征,许多学者根据这个特征进行分形研究[13,18-19]。本次压汞测试获取的进汞饱和度和毛细管压力在双对数坐标系中表现出明显的双段式特征,拟合曲线斜率明显转变的点为拐点,拐点与排驱压力之间的线段的分形维数为D1,对应该样品中相对较大的孔隙;拐点与最大压汞压力之间的线段分形维数为D2,对应该样品中的中小孔隙;以本次测试的样品6为例,拐点与排驱压力之间进汞饱和度与毛管压力之间拟合的相关系数达到0.969,说明该段符合分形特征,斜率约为1.423 8(图2),根据公式(8)可以得到相应的分形维数D1为4.42,拐点与最大压力之间线段斜率约为0.19,相应的分形维数值D2取值为3.19。由于计算分形维数的数据分布在排驱压力与最大压力之间,结合本次试验的4组曲线排驱压力之上的部分进行对比,分析分形维数值代表的地质意义。
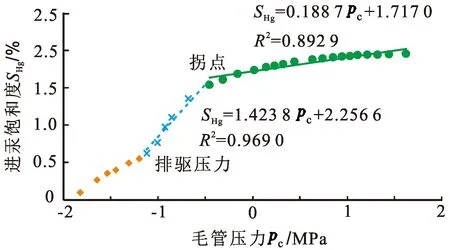
图2 分段计算分形维数示意图(样品6)Fig.2 Schematic diagram of segmented calculation of fractal dimension (sample 6)
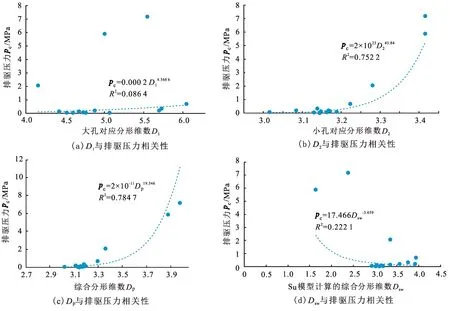
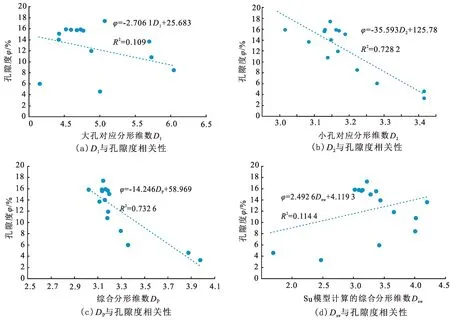
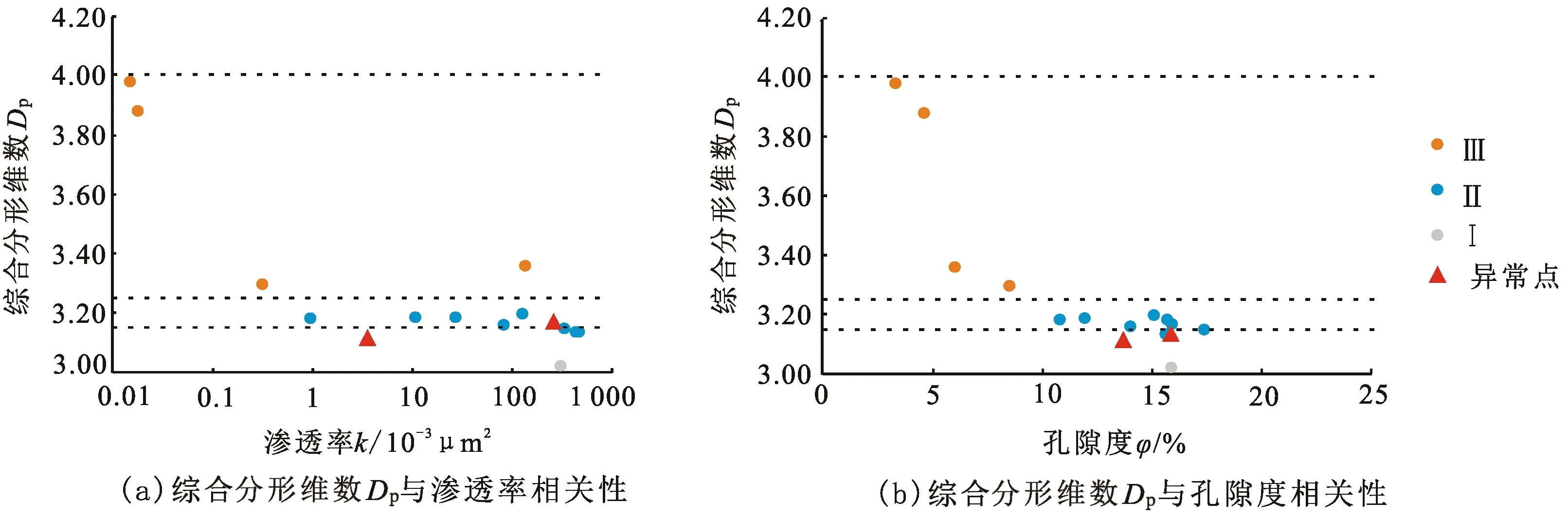
分形维数D1代表样品中较大孔隙的均一程度。本次试验提供的11、12、13、14号样品计算得到的D1分别为5.70、5.73、6.04、5.55,数值上极为接近,同一坐标系中4组曲线的D1对应段大概平行,但排驱压力11号<12号<13号<14号。实际地质条件下,D1对应段曲线的平缓程度与砂岩的分选、孔吼的均一程度有关,分选越好的砂岩对应的孔隙越均一,在压汞过程中,一旦达到该孔径对应的压力,汞流体可以在压差变化不大的情况下进入该部分孔隙。从本质上讲,该段压汞曲线的平缓程度取决于排驱压力与拐点压力之间的差值,或者说是2个节点孔隙半径的差值,差异越小对应的曲线越平缓,管束状模型对应的毛细管越能自由弯曲,相应的分形维数值D1越大。事实上,储层的物性与均一程度并无必然联系,均一程度较高的碎屑岩只有孔隙较大(排驱压力较小时)才能具备较高的渗透率。计算得到的分形维数D1十分接近甚至超过毛细管束模型的上限6(其中1 分形维数D2与拐点压力密切相关,拐点压力与进汞饱和度中值压力接近。本次试验的全部15组样品中,最大的毛细管压力约为42 MPa,与之对应的孔隙半径为0.018 μm,该压力下对应的进汞饱和度有13组样品分布在70%~90%,即坐标系中D2对应的压汞曲线段上部端点极为接近,曲线的斜率主要受控于拐点的位置,拐点对应的压力越低,因为双对数坐标系中Logpc为横坐标,相应的D2对应的斜率越小,计算得到的分形维数值越小(表1),以11、12、13号3组样品为例,其最大进汞压力与进汞饱和度基本重合,11号样品具有最低的拐点压力,相应的分形维数值最低为3.08,而13号样品对应的拐点压力最大,计算得到的D2为最大的3.22。 考虑到压汞曲线中分段描述的曲线分形维数值不能整体表达岩石孔隙的不均一程度,Su等[13]尝试使用加权的方法求取综合分形维数,其模型中的综合分形维数Dsw满足: Dsw=D1Sinf+D2(Smax-Sinf). (9) 式中,Dsw为Su等[13]模型中的综合分形维数;Sinf为对应于分形曲线拐点对应的饱和度,%;Smax为压汞曲线中的最大饱和度,%。 从图2中可以看出,压汞分形曲线的拐点之后,对应的中小孔隙对进汞饱和度的贡献较小,Sinf明显大于(Smax-Sinf),即相对较大孔隙对应的D1被人为加大,而D1仅代表较大孔隙的均一程度,与储层物性无法直接对应,Dsw指标评价储层时可能出现明显的偏离,以样品14和15号为例,对应的数值分别为2.47、1.69,是所有15组样品中综合分形维数值最小的样品,对应的物性参数渗透率为0.02×10-3μm2,孔隙度全部小于5%,显然Dsw与储层孔渗并未表现出正相关的规律。 图3 分形维数分段计算对应的进汞曲线Fig.3 Corresponding mercury injection curve of fractal dimension calculation 为了表征整个样品全孔径范围的分形特征,拟采用加权平均的方法确定综合反映整个样品特征的分形维数Dp,而权重由所在线段的毛细管压力差决定,具体公式为 Dp=D1(ΔpD1/p)+D2(ΔpD2/p). (10) 式中,ΔpD1为拐点压力与排驱压力的差值,代表孔径较大的低压区毛细管压力差,MPa;ΔpD2为大于拐点压力的高压区毛细管压力差,MPa;p为整体毛细管压力差,为ΔpD1与ΔpD2之和,MPa。数值上等于最大的毛细管压力减去排驱压力,本次压汞试验最大的毛细管压力基本相等,全部约为42 MPa,该数值与压汞仪型号有关,p为整体毛细管压力差,数值与样品的排驱压力有关,排驱压力越大,相应的p越小。当样品中较大的孔隙相对均匀时,D1基本接近,而权值ΔpD1/p与排驱压力有关,排驱压力增大、毛细管压力差减小、D1权值增大。D2仍代表中小孔隙的贡献,其权值与D1权值之和为1。由此可以看出,综合分形维数Dp中不仅考虑较大孔隙的均匀程度、排驱压力(大孔孔径),同时考虑中小孔隙的贡献。 实验室获取的储层评价参数除了孔隙度、渗透率等直接参数外,利用压汞获取的排驱压力、饱和度中值压力也常应用到储层评价中。相对致密、孔隙度较小的岩石一般具有较高的排驱压力和较高的中值压力。Pittman E D提出利用孔喉半径Rapex指标评价储层物性的方法,Rapex对应Pittman图(汞饱和度作横坐标、汞饱和度/毛细管压力为纵坐标的图)的顶点的孔喉半径,表示单位压力下进汞最快的点,Rapex与排驱压力负相关,与孔隙度和渗透率正相关。本次获取的15组试验数据表明,排驱压力与Rapex相关系数达到0.99,Rapex与渗透率、孔隙度的相关系数也达到0.93和0.70(图4),表明Rapex是一种良好的评价储层的参数。 利用分形几何方法处理得到的分形维数,与上述储层评价的5项参数建立联系后(图5~9),才能应用到储层评价过程中,15组样品分析结果表明:对应较大孔隙统计段分形维数的D1与各项参数相关性极差。D1除了与渗透率弱相关外(相关系数为较低的0.46),与排驱压力、饱和度中值压力、Rapex、孔隙度等4项参数之间基本不具备相关性,相关系数绝大多数不足0.1。其根本原因在前文已经表述,D1仅代表样品大孔部分的均一程度,类似样品11、12、13号的含粗粉砂含细粉砂和黏土极细砂岩—极细砂细砂岩,因位于三角洲前缘,即便具有较好的分选,因碎屑颗粒粒径小、孔径小,相应的排驱压力、中值压力较大,微孔虽然具备一定的孔隙度,但渗透率被极大的限制。同样分选较好的3~9号样品(表1),因颗粒大、孔径大,分形维数D1相差不大的条件下,孔渗参数明显优于样品11~15。 图4 储层物性与Rapex之间的关系Fig.4 Relationship between reservoir properties and Rapex 对应中小孔隙统计段分形维数的D2与各项参数具有较好的相关性。D2与样品的排驱压力、中值压力、Rapex、孔隙度的相关系数全部大于0.7,与渗透率的相关性略低,仍达到0.508。前已述及,本次获取的15组样品中D2与拐点压力有直接关系,而拐点压力与饱和度中值压力极为接近,由此导致D2与其他评价参数相关性较高。 Su等[13]提出的综合分形维数Dsw指标与本次测试的15个样品物性参数相关性差,且出现规律的背离。Dsw指标与中值压力的相关系数为0.11,与排驱压力相关系数为0.21,与渗透率Rapex指标相关系数为0.2,与渗透率相关系数为0.02,与孔隙度相关系数为0.1,说明该指标在珠江口盆地应用效果极差。在相关规律上,随着综合分形维数Dsw增大,孔隙越复杂,却出现渗透率、孔隙度、Rapex增大,而排驱压力、中值压力降低的现象,明显背离地质规律。可见人为的增大D1的权值并不能增大该部分孔隙对渗透率的贡献度,根本原因仍在于单独的D1指标仅代表大孔的均一程度,与大孔的孔径无关。 图5 分形维数与排驱压力的相关性Fig.5 Correlation between fractal dimension and displacement pressure 图6 分形维数与饱和度中值压力的相关性Fig.6 Correlation between fractal dimension and saturation median pressure 本次改进的综合分形维数Dp与各项储层指标相关性更好。Dp与排驱压力、中值压力、Rapex、渗透率、孔隙度的相关系数依次为0.79、0.85、0.77、0.64、0.74,全部高于前述3个指标中最好的D2指标,对应相关系数依次为0.75、0.77、0.73、0.51、0.73。 基于以上的分析可以得知,在反映孔隙结构的异质性和复杂性上,Dp不仅比D1和D2而且比Dsw有更令人满意的结果,并从数学角度更好的表征孔隙结构多尺度特征,可作为孔隙结构分类和评价良好参数。 图7 分形维数与Rapex的相关性Fig.7 Correlation between fractal dimension and Rapex 图8 分形维数与渗透率的相关性Fig.8 Correlation between fractal dimension and permeability 图9 分形维数与孔隙度之间的关系Fig.9 Relationship between fractal dimension and porosity 综合分形维数Dp与储层物性的良好相关性表明,可以作为不同类型储层的定量指标。按照石油天然气总公司的的储层分类标准,先对储层进行评价再与参数Dp结合,形成一个大致的分类标准。经过评价后的结果展示在表2中,按照评价结果将3.14和3.25作为Dp的分类评级标准,小于3.14为Ⅰ,3.14~3.25为Ⅱ,大于3.25为Ⅲ(图10)。利用Dp指标划分的储层类型,与孔隙度、渗透率实测指标划分的类型基本吻合,本次测试得到的15组样品中13组相吻合。偏离的两组数据中,9号样品综合分形维数Dp为3.17,11号样品的Dp为3.11,因与分类的边界值3.14极为接近,类型划分时略有偏差。整体上综合分形维数Dp指标在划分储层类型上仍具备较大的可信度。 表2 评价结果Table 2 Evaluation results 图10 两种参数评价分类Fig.10 Classification diagram for evaluation of two parameters (1)在双对数坐标系中进汞饱和度与毛细管压力拟合相关系数一般大于0.85,说明压汞曲线具备分形要求的自相似特征;任意段拟合曲线的分形维数Di与曲线斜率k满足Di=3+k,分形维数Di由孔隙空间的分形维数Df和毛细管曲折度分形维数DT共同构成,管束状模型中Di的理论值分布在3~6,如考虑毛细管相互交叉、联通对储层孔吼的复杂化,分形维数理论值的上限可能超过6。 (2)分段计算得到的分形维数值具有不同的地质含义,压汞曲线中大于排驱压力的相对平缓段,对应样品中较大的孔隙,双对数坐标系中求取的相应分形维数值D1仅代表该部分孔隙的均一程度,而与储层的孔吼半径(或者排驱压力)无必然关系,故D1与储层孔渗参数无相关性,综合分形维数Dsw求取过程中,人为的增大D1的权值,可能造成综合分形维数与排驱压力、中值压力、孔隙度、渗透率等储层评价参数的相关性低,甚至出现规律性错误;压汞曲线中大于拐点压力部分求取的分形维数值为D2,该数值与拐点压力有明显关系,而拐点压力十分接近于饱和度中值压力,因此D2与储层物性有直接联系。 (3)改进后的综合分形维数Dp求取时,利用D1表征孔隙的均一程度,D1的权值ΔpD1/p与排驱压力有关,两者乘积共同表征大孔隙对储层物性的贡献度,D2与其权值的乘积表征中小孔隙对物性的贡献,求取得到的综合分形维数Dp与排驱压力、中值压力、Rapex、渗透率、孔隙度的相关性全面优于D2、D1、Dsw等指标;综合分形维数Dp小于3.14、3.14~3.25、大于3.25等3个区间段,与石油行业储层分类标准的Ⅰ类、Ⅱ类、Ⅲ类储层具有良好的对应关系。2.3 综合分形维数Dsw的计算

2.4 综合分形维数Dp的计算
3 分形维数与储层评价参数的耦合关系
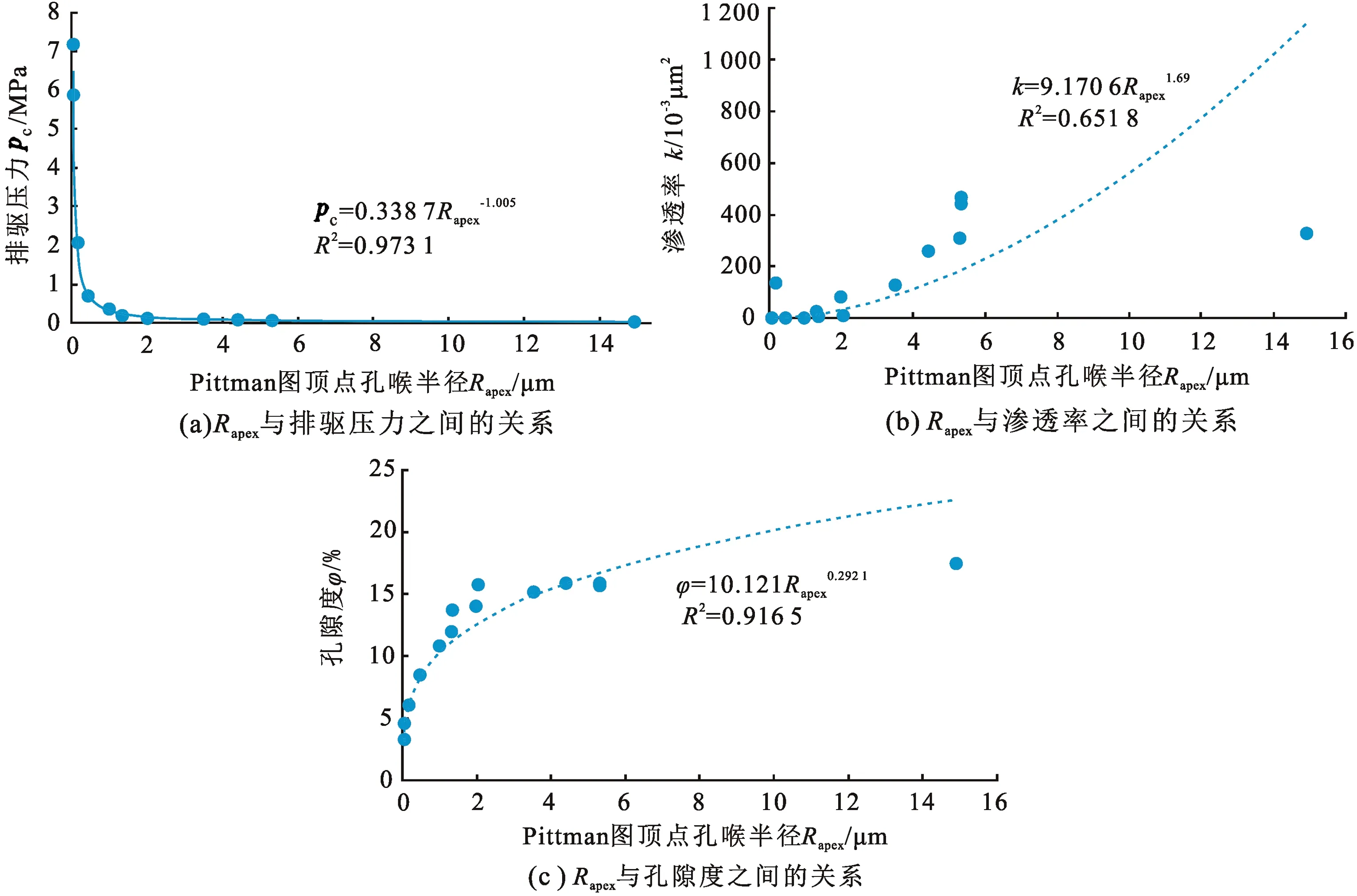



4 综合分形维数Dp在储层评价中的应用
5 结 论
