联合EMD和分数阶Fourier变换的裂缝性火成岩地层纵波和横波时频特征

2022-01-18徐方慧王祝文王文华齐兴华崔裔曈韩锐羿

中国石油大学学报（自然科学版） 2021年6期

徐方慧,王祝文,王文华,齐兴华,崔裔曈,韩锐羿

(1.吉林大学地球探测科学与技术学院,吉林长春 130026;2.吉林大学地球科学学院,吉林长春 130021)

火成岩储层中裂缝是重要的储集空间,裂缝的发育情况与储层的渗透性和储集性息息相关[1-2]。地层中缝洞构造会影响阵列声波测井信号的能量、频率和时差[3-4],故掌握声波信号对裂缝的响应规律是非常重要的。在实际应用中,阵列声波测井信号成分复杂,同时包含高频的纵、横波和低频的斯通利波,属于非平稳、非线性的复杂信号,为了同时获得声波信号频域和时域的特征,时频分析方法被引入到信号处理中。王祝文等[5]利用Choi-Williams时频分布,分析了以岩性为变量的构造破碎带声波信号的能量特征。向旻[6]提取了不同角度和充填类型的裂缝的声波信号时频分布,结果显示Choi-Williams分布能够直观地显示裂缝对各组分波在时间和频率上的影响。纵波和横波会受到地层裂缝不同程度的影响[7-11]。阵列声波测井信号中不同组分的波在能量和频率上相差大,纵波和横波的幅值往往较小(特别是纵波),在同一个时频分布图中很难将所有信号同时展现出来,所以需要将纵波和横波分别提取出来单独研究。经验模态分解[12-13](empirical mode decomposition,EMD)由希尔伯特-黄提出,可从非平稳的待处理信号中分解得到数量不固定的较为平稳的固有模态函数(intrinsic mode function,IMF),它能够有效地从阵列声波数据中将纵波和横波整体提取出来,但不能彻底分离纵、横波[7]。为了将纵波和横波信号有效分离,考虑利用滤波手段从频域入手。Fourier变换受到原始信号平稳性的限制,直接采用Fourier变换对声波滤波不能取得好的效果。为了改善该问题,学者们引入了一种较新的、应用较为广泛的数学方法——分数阶Fourier变换(FRFT)[14-15]。Almeida[16]将FRFT解释为一种“角”Fourier变换,即一种由信号沿着时频平面内的坐标轴绕其原点旋转任意角度后构成的分数阶Fourier域上的表示方法。Qzaktas等[17]通过公式推导得出一个结论,若核函数关于原点旋转对称,那么FRFT的Cohen类分布[18]可以由原信号的Cohen类分布旋转得到,再一次有力地印证了FRFT作为一种旋转转子的观点。纵波和横波信号存在较强的时频耦合,若利用FRFT的旋转特性,根据实际需求把声波信号在时频平面旋转某个角度,在新的FRFT域中消除纵波和横波的时频耦合,从而通过滤波实现分离纵波和横波的目的。Choi-Williams分布[19-21]作为一种典型的Cohen类双线性时频分布,能有效抑制交叉项的影响。笔者利用EMD把纵波和横波从原始声波信号中整体提取出来,然后根据FRFT的旋转特性对声波信号的时频分布进行滤波,选择Choi-Williams分布处理裂缝性火成岩地层的阵列声波测井信号。

1 EMD原理

EMD的分解模式受信号频率控制,能从复杂的非平稳信号中提取若干频率逐渐降低的相对稳定的IMF。对任意阵列声波测井信号s(t)进行EMD分解的步骤[12-13]为:

(1)找出信号极值点并确定极值点的上下包络线。记上下包络均值为m1(t),则有

s(t)-m1(t)=h1(t).

(1)

式中,h1(t)为声波测井信号s(t)与上下包络均值m1(t)的差,h1(t)和m1(t)的下标数字表示筛选次数,此时为第一次筛选。首先判断h1(t)是否为一个有效的IMF。判断一个IMF是否有效可以参考以下依据[12-13]:一是在一个IMF所有时间点上极值点与零点的个数差值不大于1;二是一个IMF在任意时间点局部最值的上、下包络均值为0。

(2)假如h1(t)判断为不是有效的IMF,则把h1(t)作为原始信号,重复步骤(1),反复筛选k次,得到hk(t)=h(k-1)(t)-mk(t),使得hk(t)满足IMF的条件。令c1(t)=hk(t),则c1(t)为信号s(t)的第一个频率最高的IMF。

(3)将c1(t)从原始信号s(t)中分离出来,得到

r1(t)=s(t)-c1(t).

(2)

式中,r1(t)为声波测井信号s(t)与第一个IMF的差。将r1(t)作为原始信号重复步骤(1)和(2),循环n次得到信号s(t)的第n个IMF分量。最终

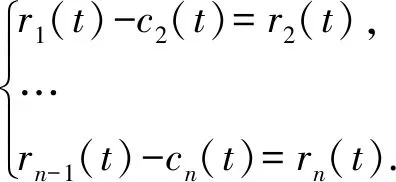
(3)

经过整理有

(4)

式中,cj(t)为IMF分量,j表示第j个IMF;rn(t)为残量,一般是一个单调函数，其下标数字n表示循环次数。IMF包含原信号的固有物理性质。由于不同组分的声波信号频率上有一定的差异,所以EMD适合用来处理声波信号。高频的IMF往往包含原始信号大量的信息。

2 FRFT的原理

一般在u域的函数f(u)的p阶的FRFT定义为

(5)

其中

Kp(u,u′)=Aαexp[jπ(u2cotα-2uu′cscα+u′2cotα)],

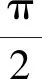
图1 (t,ω)平面旋转α角度到(u,υ)平面Fig.1 (t,ω)plane to (u,υ)plane after rotateing α degrees

FRFT有如下几个重要性质[15]:

(1)线性变换。FRFT是线性变换,它满足叠加原理,即

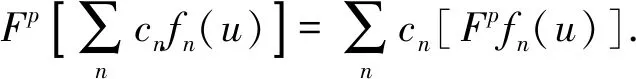
(6)

式中,cn为任意复常数;n为任意整数。

(7)

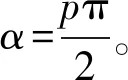
通过以上分析可知FRFT属于广义Fourier变换,是一种重要的时频分析工具,特别是利用FRFT的旋转特性处理来信号,可以揭示该信号在不同阶数下的时频分布特征。本文中将利用FRFT的性质(式(2)和(3)),同时结合EMD对声波信号滤波最终提取纵波和横波时频特征。

3 Choi-Williams分布

信号x(t)的Cohen类时频分布[18]为

exp(-i2π(iυ+fτ-uυ))dudυdτ.

(8)

式中,p(t,f)为信号x(t)的Cohen类时频分布;υ为频移;u为时间积分变量;t为时间;f为频率;g(τ,υ)为核函数,核函数不同,则可以用来表示不同的Cohen类时频分布。Cohen类时频分布的本质属性是二维傅里叶变换,其存在一个不可消除的交叉项。

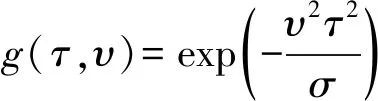
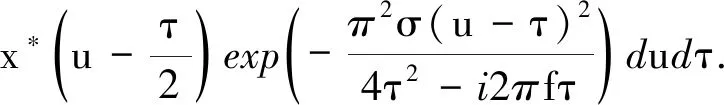
(9)

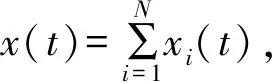
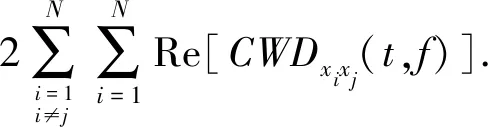
(10)

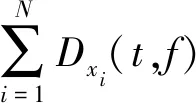
4 裂缝性火成岩地层纵波和横波的时频特征

本文中选择辽河东部凹陷盆地火成岩地层的多极子阵列声波测井数据。图2给出了致密火成岩地层中某一深度的阵列声波信号及其部分IMF的Choi-Williams分布。

图2(a)中从下到上8条曲线分别为单极子阵列声波测井中8个探头接收的不同源距的声波信号。探头1的源距为3.658 m,每个探头之间的距离为0.152 m。图2(b)中原始声波信号signal为探头1接收的声波信号,对其进行EMD分解后得IMF1-6和残量res,可以看出每个IMF包含原始声波信号signal不同组分的波。图2(c)为原始声波信号signal的Choi-Williams分布,致密火成岩地层中声波信号的幅值很高。图2(c)中显示能量主要分布在波峰时间2.8 ms、主频4 kHz的斯通利波中;由于纵波和横波的幅值很小,在图2(c)中不可见。图2(d)为IMF1的Choi-Williams时频分布。由图2(b)和(d)可知,IMF1很好地对应原始声波信号signal中的纵波和横波。图2(d)中纵波轻微可见,主频为10.5 kHz,波峰时间为1 ms;横波主频为10 kHz,波峰时间为1.8 ms。图2(e)和(f)中分别给出了IMF2和IMF3的Choi-Williams时频分布,主要包含高频和低频斯通利波。图2说明EMD能够有效地将声波信号中频率相差较大的波分开,即可将纵、横波与斯通利波分离,但不能分离频率接近的纵波和横波。本文中利用FRFT旋转特性对IMF1滤波来提取纵波和横波。

图3(a)和(b)为致密火成岩地层中IMF1的Choi-Williams分布,其中图3(a)为三维立体图,图3(b)为平面等值线图。图3(a)和(b)中显示横波周围存在很多干扰波,甚至覆盖了整个频率域。有3个原因:一是Choi-Williams分布算法虽能抑制交叉干扰项,但不能完全将其消除;二是伪瑞利波带来的干扰;三是可能声波测井仪器本身或井孔环境形成的干扰波。由图3(a)和(b)可知,纵波的主频为10.5 kHz,横波频率低于纵波,高于斯通利波和伪瑞利波,而且横波到时在纵波之后。为了降低这些干扰波对后续滤波过程的影响,同时保留图3(b)红框中的横波,选择截止频率8～12 kHz对IMF1分量做带通滤波。图3(c)和(d)为经过带通滤波的IMF1的Choi-Williams分布。由图3(c)和(d)可知,经过滤波的IMF1中干扰波明显减少,且横波幅值没有降低,纵波和横波已清晰可见。

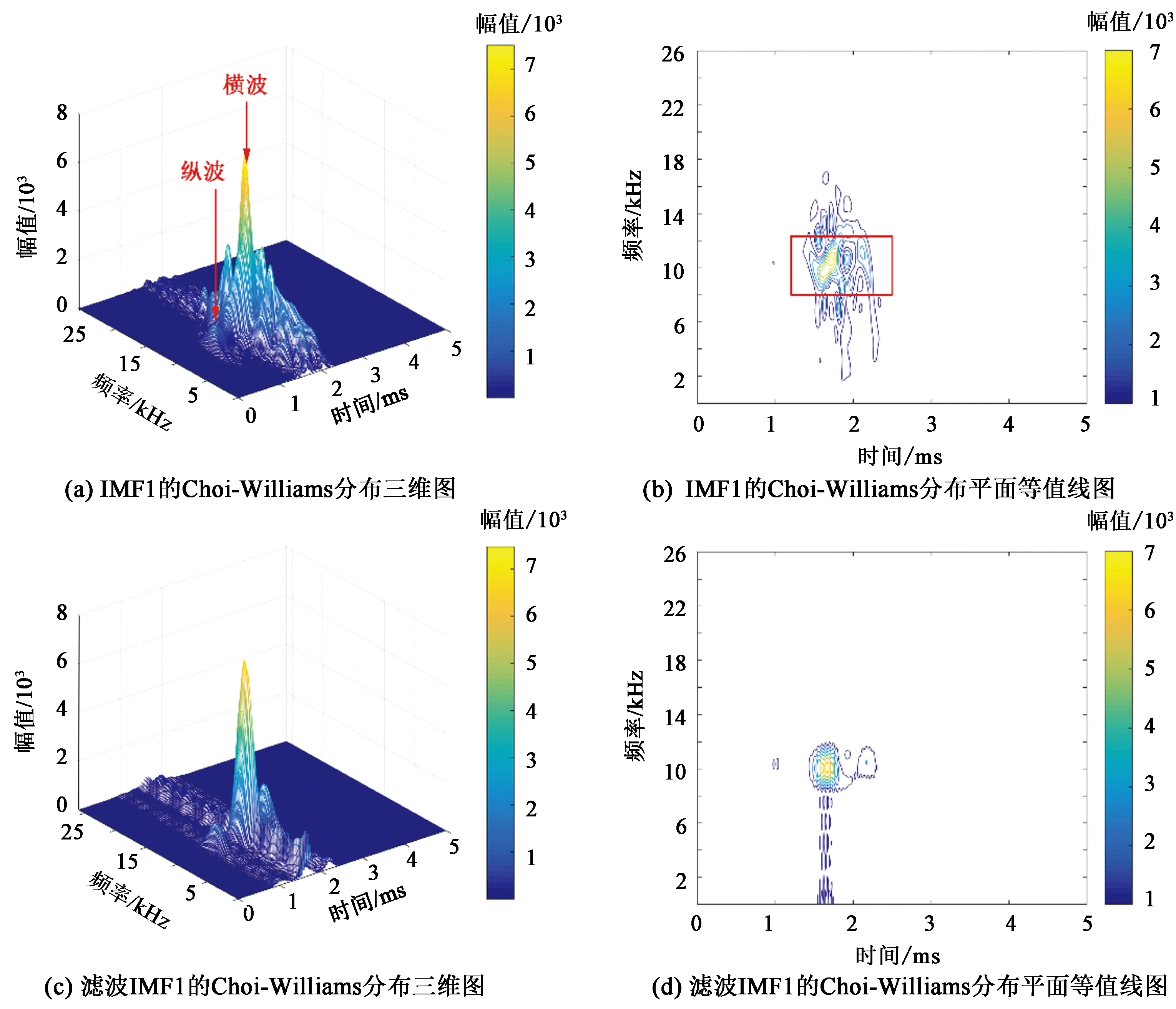
图3 致密火成岩地层IMF1和滤波IMF1的Choi-Williams分布Fig.3 Choi-Williams distributions of IMF1 and filtered IMF1 in tight igneous formation

图4为滤波IMF1经过不同阶数FRFT处理的Choi-Williams分布。图4(a)为滤波IMF1的Choi-Williams分布,可看作经过0阶FRFT处理,此时纵波和横波在频率域耦合非常严重,进行频域滤波不可能将它们分开。图4(b)～(d)分别为滤波IMF1经过0.15、0.3和0.45阶FRFT处理得到的。随着FRFT阶数的增加,滤波IMF1的Choi-Williams分布旋转的角度也随之增加。图4(b)中FRFT的阶数为0.15,纵波主频为16 kHz,横波主频为13 kHz,频率域中纵波和横波的耦合不再严重;图4(c)中FRFT的阶数为0.3,纵波主频为21 kHz,横波主频为16 kHz;图4(d)中FRFT阶数为0.45,纵波主频为25 kHz,横波主频为18 kHz。随着FRFT的阶数增加,纵波和横波主频的分离程度增大,在频率域使用滤波器完全能够将纵波和横波分离。

值得注意的是,滤波时FRFT阶数的选择不是固定的。利用FRFT的旋转特性是为了消除纵波和横波频率域的耦合现象,同时使纵波和横波尽可能大地分开,以达到通过滤波器将其提取出来的目的。纵波和横波频率接近,若FRFT阶数太小,纵波和横波不能完全分开,它们的滤波参数可能会重叠,从而影响滤波结果,所以处理过程中需要选择合适的FRFT阶数。图5(a)和(b)分别为滤波IMF1经过0.3和0.45阶FRFT的结果。图5(a)中纵波的带通滤波频率为20～23 kHz,图5(b)中纵波的带通滤波频率为23～26 kHz,滤波结束后对信号分别进行0.3和-0.45的FRFT逆运算将其反方向旋转回来。图5(c)和(d)分别为经过0.3和0.45阶FRFT的纵波滤波结果。经过0.3和0.45阶FRFT后的去噪IMF1中纵波和横波分离均比较明显,所以二者除了波峰形状有细微的差别,主频、到时和波峰幅值没有差别,这也进一步验证了FRFT作为旋转转子的合理性。若选择0.15阶的FRFT进行滤波,提取的纵波仍会受到横波的影响。

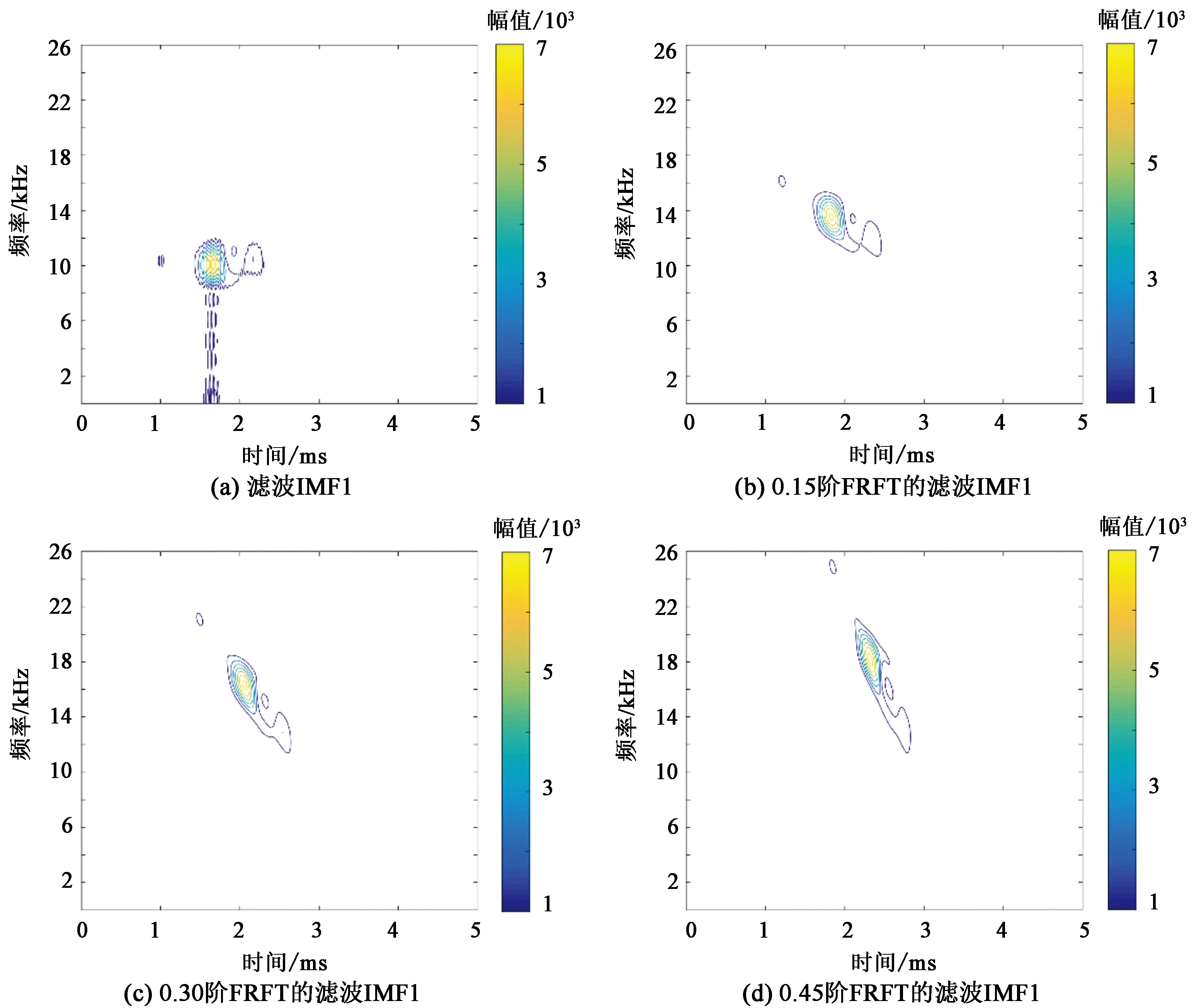
图4 滤波IMF1不同阶数FRFT的Choi-Williams分布Fig.4 Choi-Williams distributions of filtered IMF1 of FRFT with different orders

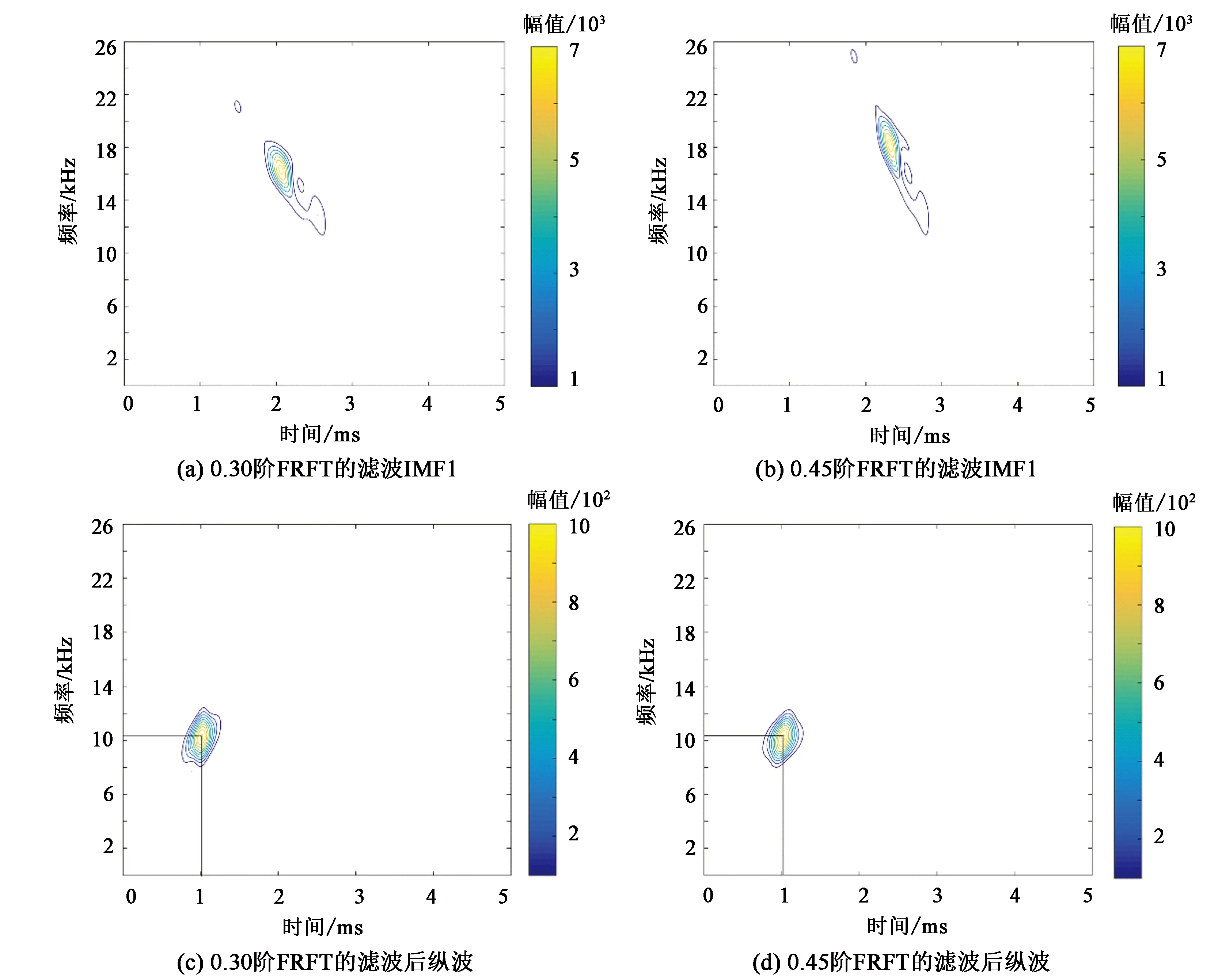
图5 不同阶数FRFT的纵波Choi-Williams分布Fig.5 Choi-Williams distributions of P wave of FRFT with different orders

选择FRFT的阶数为0.45。致密地层中纵波设置带通滤波的截止频率为23～26 kHz,横波设置带通滤波的截止频率为16～21 kHz。图6(a)和(b)为提取的纵波的Choi-Williams分布。图6(a)中滤除横波后只显示纵波峰值,图6(b)显示纵波的主频为10.5 kHz,到时为1 ms,幅值为1 000,与IMF1分量中的纵波对应很好。图6(c)中滤除纵波后只显示横波峰值,图6(d)显示横波的主频为10 kHz,到时为1.6 ms,幅值为7 000,同样与IMF1分量中的横波对应很好,这说明联合EMD和FRFT对声波信号滤波是有效的。

探究裂缝的纵、横波时频特征时需要在其他影响因素保持一致的前提下进行。在数据选择过程中,为了尽可能减少其他因素的影响,在地层岩性、井径相同的情况下,选择同一口井中裂缝倾角不同的两条声波曲线与致密地层的声波时频特征进行对比。图7为低角度裂缝火成岩地层阵列声波信号的IMF及其Choi-Williams分布。观察图7(a)原始声波信号signal和IMF1可知,横波幅值已经低于纵波。图7(b)中纵波和横波幅度微弱,图7(c)中只能观察到斯通利波。

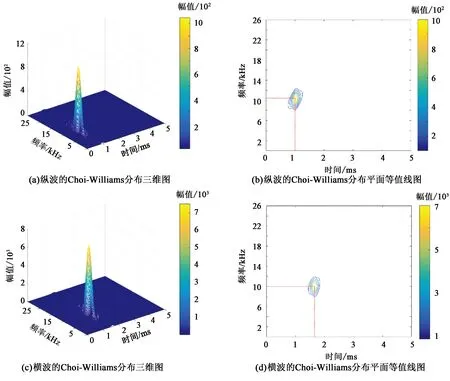
图6 致密火成岩地层纵波和横波的Choi-Williams分布Fig.6 Choi-Williams distributions of P and S wave in tight igneous formation

图8(a)和(b)为低角度裂缝火成岩地层IMF1的Choi-Williams分布。能看出纵波和横波频率耦合现象严重,按照上述方法对低角度裂缝的IMF1进行滤波处理,得到纵波的Choi-Williams分布(图8(c)和(d))以及横波的Choi-Williams分布(图8(e)和(f))。图8(c)和(d)中纵波的主频为9 kHz,波峰时间为1.15 ms,幅值为700,与IMF1中纵波对应好;图8(e)和(f)中横波的主频为8.5 kHz,波峰时间为1.9 ms,幅值为250,与IMF1中横波对应好。

图9为高角度裂缝火成岩地层阵列声波信号的IMF及Choi-Williams分布。图9(b)中显示有横波可见,纵波幅度很小,图9(c)中除了斯通利波也可见横波。

图10(a)和(b)为高角度裂缝火成岩地层IMF1的Choi-Williams分布。同理对高角度裂缝火成岩地层IMF1进行滤波处理,得到图10(c)和(d)纵波的Choi-Williams分布以及图10(e)和(f)横波的Choi-Williams分布。图10(c)和(d)中纵波的主频为9.5 kHz,波峰时间为1.05 ms,幅值为450,与IMF1中纵波对应很好;图10(e)和(f)中横波的主频为8.5 kHz,波峰时间为1.75 ms,幅值为3 000,与IMF1中横波对应很好。

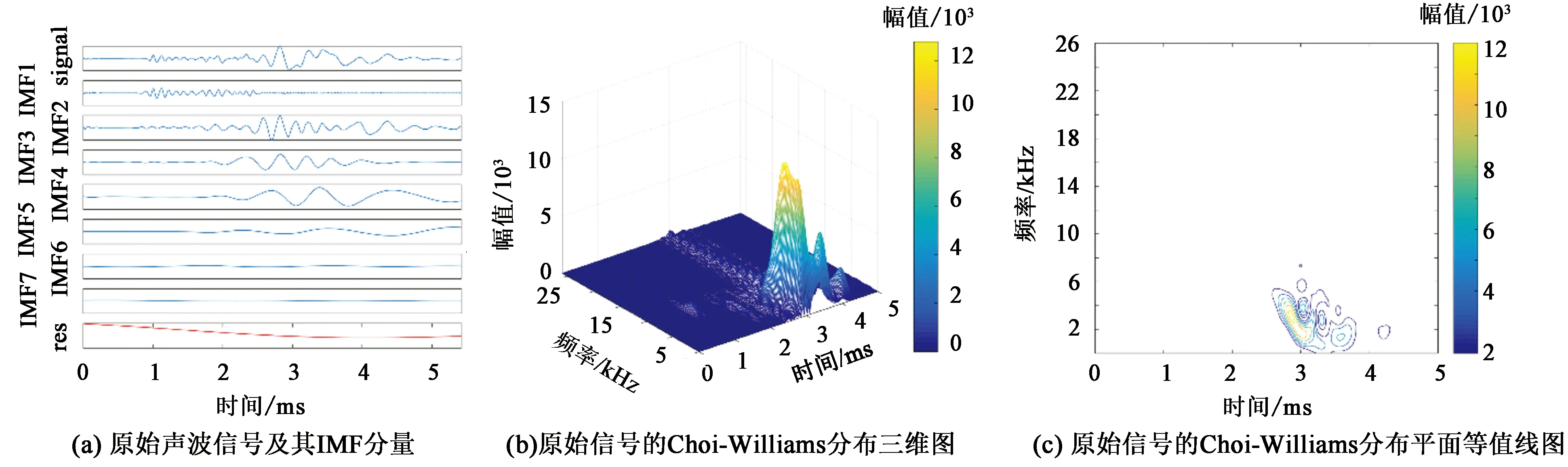
图7 低角度裂缝阵列声波信号的IMF和Choi-Williams分布Fig.7 IMF and Choi-Williams distribution of array acoustic signal with low angle fractures

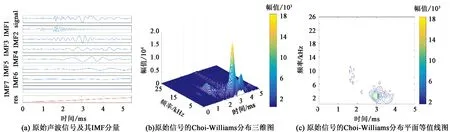
图9 高角度裂缝阵列声波信号的IMF和Choi-Williams分布Fig.9 IMF and Choi-Williams distribution of array acoustic signal with high angle fractures

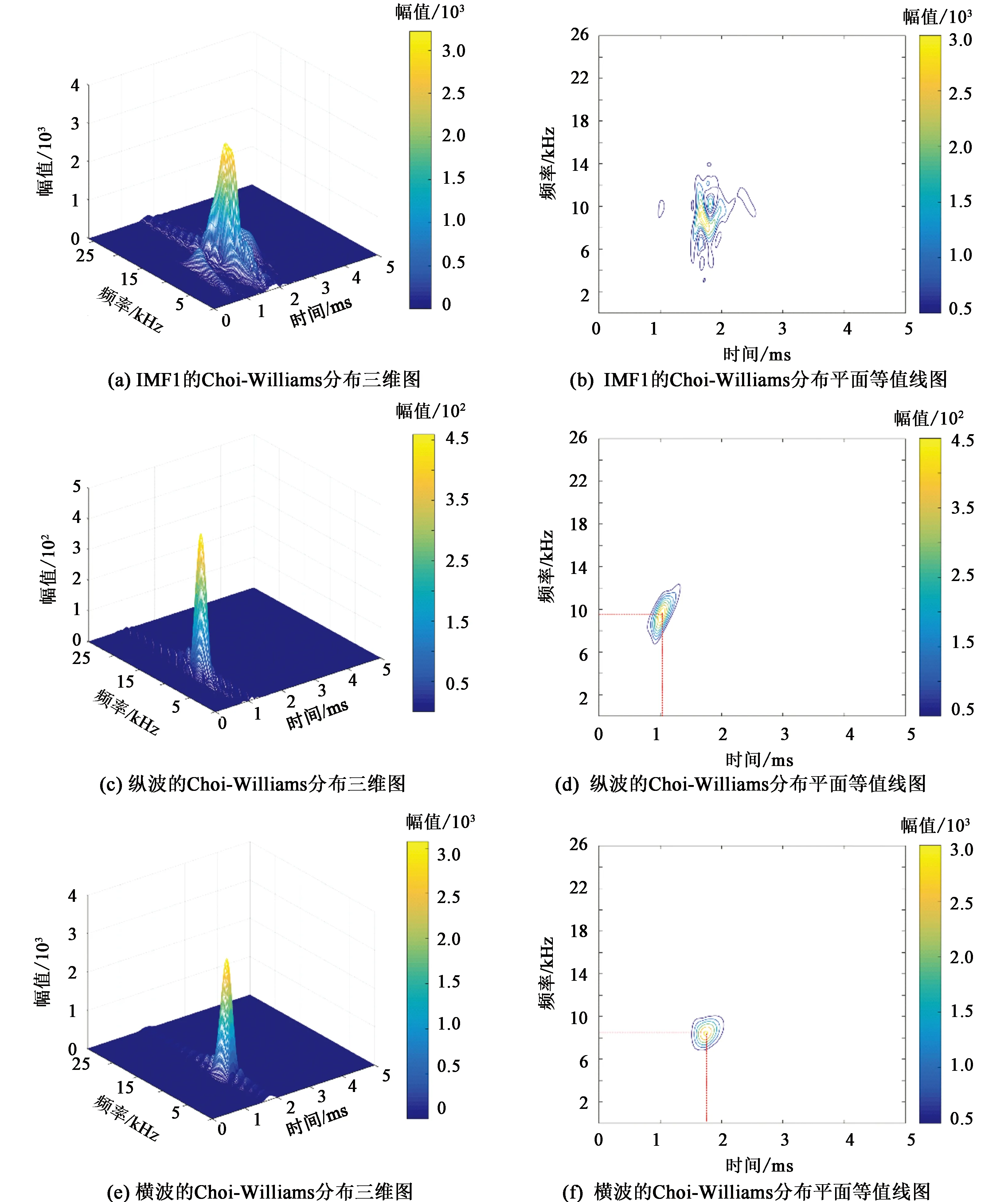
图10 高角度裂缝火成岩地层IMF1、纵波和横波的Choi-Williams分布Fig.10 Choi-Williams distributions of IMF1,P and S wave in igneous formation with high angle fractures

5 分析与讨论

由上述结果可知,声波信号IMF1的Choi-Williams分布在Fourier域中纵波和横波时频耦合严重,但在FRFT域中纵波和横波能有效分离,说明FRFT能够有效解决信号时频耦合的问题。图4中FRFT阶数越大,纵波和横波主频分离程度越大,更有利于信号的滤波处理。在实际应用中,需要根据信号自身特征与处理需求来选择FRFT正变换、逆变换以及最合适的阶数。

相对于致密火成岩地层,无论低角度还是高角度裂缝都会使地层纵波和横波的幅值、频率和波峰时间发生不同程度的变化。在幅值方面,图6中致密地层中纵波幅值为1 000,横波幅值为7 000。图8中低角度缝对应的纵波幅值为700,相对于致密地层衰减较小;横波幅值为250,衰减相当严重。图10中高角度缝对应的纵波幅值为450,相对于低角度缝来说,纵波幅值衰减反而增大了;横波幅值为3 000,与低角度缝相比,横波幅值的衰减变小。因为致密火成岩地层渗透性低且无有效孔隙和缝洞,对声波信号影响很小,故声波幅值大且稳定。当地层中存在裂缝时,纵、横波穿过裂缝时有模式波转换,故透射能量发生衰减。透射系数决定透射能量的大小,而透射系数直接受到裂缝倾角的影响,纵、横波跨越裂缝带时,由裂缝传递的能量一般由裂缝分界面波的模式转换效率控制。假设裂缝饱含水,地层传播的纵、横波在遇到第一个岩石-水分界面时,会发生第一次模式波转换,即转换成流体中的波;在第二个水-岩石分界面处发生第二次模式波转换,故裂缝的倾角能够直接对纵、横波产生影响。Morris等[22]研究指出,当纵波通过水平缝时几乎没有衰减,随着裂缝角度的增加,纵波衰减逐渐增加;横波通过低角度缝时,衰减最严重,随着裂缝倾角的增加,横波衰减反而减小。这种解释适用于本文的结果,纵波幅值在高角度缝中衰减更多,而横波幅值在低角度缝中衰减更多。

在频率方面,图6中致密火成岩地层纵波主频为10.5 kHz,横波主频为10 kHz。图8中低角度裂缝地层纵波主频为9 kHz,横波主频为8.5 kHz。图10中高角度裂缝地层纵波主频为9.5 kHz,横波主频为8.5 kHz。裂缝使纵波和横波的主频降低,说明纵、横波的高频能量更容易衰减。纵波和横波主频在低角度和高角度裂缝地层中降低程度差别不大。

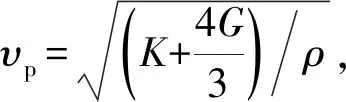
声波信号成分复杂,不同组分波在频域和时域上都有一定差异,对声波信号的解释无论是小波变换、小波包变换还是短时傅里叶变换等,其本质都是利用傅里叶变换将声波信号完全转换到频率域。FRFT的出现为声波时频分析与解释提供了新的思路,在FRFT域中不同性质地层的声波信号可能会呈现出新的差异,而这些差异可以为储层的解释和评价提供更多的依据。利用FRFT探索阵列声波信号在不同地层中的时频特征是具有潜力且有意义的,同时声波测井记录的为阵列信号,如何将FRFT提取的纵、横波信息应用到阵列声波数据中也是值得研究的课题。