VTI介质地震波群速度三维扩展各向异性线性近似表征

梁 锴,曹丹平,孙上饶,张佳佳,印兴耀

(中国石油大学(华东)地球科学与技术学院,山东青岛 266580)

地球介质广泛存在波动各向异性,而TI介质是常见的各向异性介质之一,许多专家和学者对各向异性介质的地震波正反演问题进行了深入的研究[1-3]。速度是研究地震波传播规律和描述介质特性的重要参数,是弹性波传播理论中的核心内容。单一谐波等相位面传播的速度为相速度;复合波振幅包络传播的速度为群速度,称为能量速度或射线速度。Berryman[4]推导了TI介质由相速度计算群速度的理论公式,Crampin[5]将其推广到三维情况。在此基础上,吴国忱等[6-8]分别研究了TTI介质、任意空间取向TI介质和任意各向异性介质相速度和群速度的精确公式。由于这些各向异性介质群速度的精确表达式比较复杂,与各向异性参数呈非线性关系,不利于分析各向异性程度对群速度的影响,在实际应用中也有诸多不便,所以许多学者对群速度的近似表征进行了重点研究。一方面,Fomel[9]、Sripanich和Fomel[10]、Hao和Stovas[11]分别研究了VTI介质和正交各向异性介质qP波相速度和群速度的非椭圆近似。Stovas和Fomel[12]提出了一种关于qP波的广义速度近似,该近似表征下相速度和群速度具有相同的形式。另一方面,Thomsen[13]对多种岩石的速度和各向异性参数进行了测量和计算,发现多数岩石具有弱各向异性的特点。在此基础上提出了弱各向异性近似,并推导了TI介质弹性波相速度和群速度的弱各向异性近似表征,该表达式形式较简单,并且是各向异性参数的线性函数,所以得到了广泛的应用,许多学者基于弱各向异性近似开展了相关工作。李磊等[14-18]研究了弱各向异性近似下TI介质、正交各向异性介质、任意各向异性介质弹性波相速度和群速度的线性表征。这些弱各向异性近似表征的适用条件是要求各向异性参数很小,而Thomsen[13]研究表明,部分岩石(例如页岩)的各向异性参数数值较大,这时弱各向异性近似就可能不再适用了。谷一鹏等[19]在研究VTI介质相速度时发现,对于Mesaverde泥页岩等强各向异性情况,qSV波的弱各向异性近似值与精确值最大相对误差超过10%,因此提出了一种扩展各向异性线性近似表征方法来研究VTI介质弹性波相速度的近似表征。目前,强各向异性情况下群速度的近似表征往往是关于各向异性参数的非线性函数,相对比较复杂。笔者根据多元函数线性化理论,将扩展各向异性线性近似方法[19]从VTI介质相速度近似表征引入到群速度近似表征中,通过构造雅可比矩阵,推导VTI介质地震波群速度三维扩展各向异性线性近似表征,进行理论分析和数值计算。

1 VTI介质弹性波群速度精确和近似表征

1.1 精确表征

VTI介质弹性波波动方程详尽描述了VTI介质中各质点在不同时刻的位移情况和弹性波在VTI介质中的传播规律。将平面波解代入VTI介质弹性波波动方程中并忽略震源项,就可以得到VTI介质的Christoffel方程。根据本征值问题解法,在Christoffel方程系数矩阵行列式为零的条件下,求解得到VTI介质弹性波相速度的精确表征[20],即

(1)

其中

D=[(2ε+f)sin2θ-fcos2θ]2+4(2δ+f)fsin2θcos2θ,

式中,VP0、VS0分别为qP波和qS波沿VTI介质对称轴传播的相速度;ε、δ和γ为Thomsen提出的表示TI介质各向异性强度的3个无量纲因子[13];θ为传播极角。

Berryman[4]和Crampin[5]推导的由各向异性介质相速度V计算群速度VG=(VGx,VGy,VGz)T的表达式[6]为

(2)

(3)

(4)

(5)

理论分析表明,qP波和qSV波群速度精确表征式(3)和(4)是参数VP0、VS0、ε、δ和传播角θ、φ的非线性函数,形式比较复杂。SH波群速度表征式(5)仅仅是参数VS0、γ和传播角θ、φ的非线性函数,而与参数VP0、ε、δ无关。

1.2 弱各向异性线性近似表征

(6)

(7)

(8)

式(6)～(8)是在Thomsen文献[13]基础上推导整理得到。理论分析发现,qP波和qSV波群速度弱各向异性近似式(6)和(7)是ε和δ的线性函数,SH波群速度弱各向异性近似式(8)是γ的线性函数,上述表达式的形式相对简单,便于讨论各向异性参数对弹性波群速度的影响。

1.3 扩展各向异性线性近似表征

虽然VTI介质弹性波群速度的弱各向异性近似表征形式相对简单,应用广泛,但是部分地层的各向异性参数数值较大(例如页岩),这时弱各向异性近似就可能不再适用。

根据高等微积分理论可以证明,由雅可比矩阵J(x0)描述的线性算子就是函数F(x)在x0点附近的最优线性逼近,也就是说,当x足够靠近x0点时,

F(x)≈F(x0)+J(x)·(x-x0).

(9)

即F(x)可在x0点进行线性化近似。

本文中将VTI介质地震波群速度的精确表征看作是各向异性参数ε、δ和γ的函数,采用扩展各向异性线性近似[19]对群速度进行表征,即将群速度精确表达式在参考点(ε0,δ0,γ0)处进行关于各向异性参数的一阶Taylor展开,通过构造雅可比矩阵来建立群速度扩展各向异性线性近似表征。

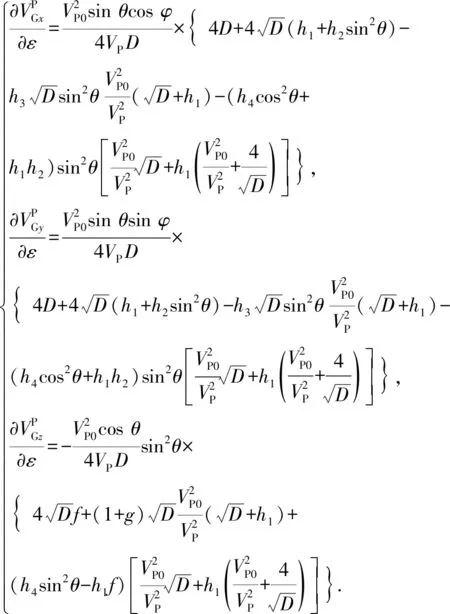
(10)

其中

(11)

(12)

(13)

(14)

由群速度精确表征与各向异性参数关系可知

(15)

由式(10)～(15)可以组成雅可比矩阵,并将参考点(ε0,δ0,γ0)数值代入其中,得到参考点(ε0,δ0,γ0)处的雅可比矩阵J(ε0,δ0,γ0),即

(16)

根据参考点处的雅可比矩阵J(ε0,δ0,γ0)和多元函数一阶Taylor展开线性化理论,可以得到VTI介质弹性波群速度扩展各向异性线性近似表征,即

(17)

(18)

同理,qSV波群速度扩展各向异性线性近似为

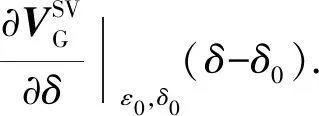
(19)

SH波群速度扩展各向异性线性近似为

(20)

qP波和qSV波群速度扩展各向异性线性近似式(18)和(19)仍然是ε和δ的线性函数,SH波群速度扩展各向异性线性近似式(20)也仍然是γ的线性函数,这说明VTI介质弹性波群速度扩展各向异性线性近似式很好地保持了群速度关于各向异性参数的线性关系,利于分析各向异性参数对群速度的影响。另一方面,理论分析证明,当参考点选为(ε0,δ0,γ0)=(0,0,0)时,群速度扩展各向异性线性近似表征就退化为弱各向异性近似表征,说明弱各向异性近似表征是扩展各向异性线性近似表征的特例,而扩展各向异性线性近似表征是弱各向异性近似表征的有效扩展。

2 数值示例

为了验证VTI介质弹性波群速度扩展各向异性线性近似式(18)～(20)的适用性,根据文献[13]选取两组VTI介质模型进行数值计算。重点考虑各向异性参数的影响,两组模型的VP0和VS0均相同,数值为VP0=2 000 m/s,VS0=1 000 m/s,各向异性参数如表1所示。其中模型A的ε<δ,且3个各向异性参数均较大,模型B的ε>δ,且部分各向异性参数较大。

表1 模型参数Tabel 1 Anisotropic parameters of models

针对模型A,由精确表征式(3)～(5)计算的群速度如图1所示,由弱各向异性近似表征式(6)～(8)计算的群速度如图2所示,在参考点(ε0,δ0,γ0)=(0.3,0.3,0.3)处由扩展各向异性线性近似公式(18)～(20)计算的群速度如图3所示。由图3可见,弱各向异性近似值与精确值存在较大差异,说明当介质各向异性参数较大时,弱各向异性近似就可能不再适用;而扩展各向异性线性近似值与精确值吻合较好,说明扩展各向异性线性近似表征能够适用各向异性参数较大的情况。为了进行对比,计算模型A的xoz面内的精确和近似群速度,如图4所示。计算两种近似群速度的相对误差如图5所示。根据图5数据计算表明,模型A中弱各向异性近似值对qP波、qSV波和SH波的相对误差最大幅值分别为6.5%、-19.2%和7.6%,而扩展各向异性线性近似值对qP波、qSV波和SH波的相对误差最大幅值分别为1.3%、-1.5%和1.3%,说明扩展各向异性线性近似表征的相对误差要明显小于弱各向异性表征。

图1 模型A群速度的精确值Fig.1 Exact value of group velocity for model A

图2 模型A群速度的弱各向异性近似值Fig.2 Weak anisotropic approximation of group velocity for model A

图3 模型A群速度的扩展各向异性线性近似值Fig.3 Extended anisotropic linear approximation of group velocity for model A

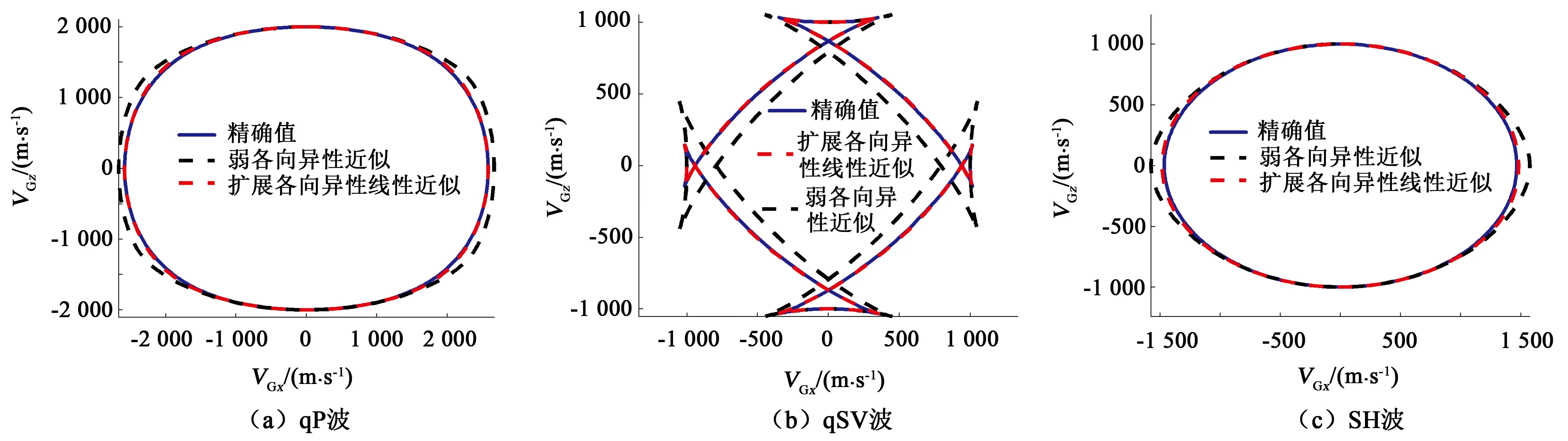
图4 xoz面内模型A的精确和近似群速度Fig.4 Exact and approximate group velocities in xoz plane for model A

同理计算模型B的精确值和近似群速度及其相对误差,如图6～10所示,其中扩展各向异性线性近似的参考点为(ε0,δ0,γ0)=(0.3,0,0.3)。根据图10数据计算表明,模型B中弱各向异性近似值对qP波、qSV波和SH波的相对误差最大幅值分别为2.3%、11.3%和5.7%,而扩展各向异性线性近似值对qP波、qSV波和SH波的相对误差最大幅值分别为0.077%、-0.11%和0.62%,同样说明扩展各向异性线性近似表征的精度较高,并且参考点的选择会影响扩展各向异性线性近似表征的精度。

图5 xoz面内模型A近似群速度的相对误差Fig.5 Relative error of approximate group velocity in xoz plane for model A

图6 模型B群速度的精确值Fig.6 Exact value of group velocity for model B

图7 模型B群速度的弱各向异性近似值Fig.7 Weak anisotropic approximation of group velocity for model B

图8 模型B群速度的扩展各向异性线性近似值Fig.8 Extended anisotropic linear approximation of group velocity for model B

图9 xoz面内模型B的精确和近似群速度Fig.9 Exact and approximate group velocities in xoz plane for model B

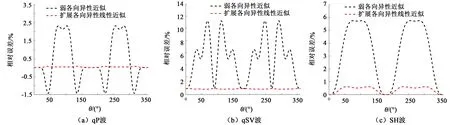
图10 xoz面内模型B近似群速度的相对误差Fig.10 Relative error of approximate group velocity in xoz plane for model B

3 结束语

根据VTI介质弹性波群速度的精确表征,将群速度函数在参考点(ε0,δ0,γ0)处进行一阶Taylor展开的线性化处理,利用雅可比矩阵推导群速度扩展各向异性线性近似表征。理论分析和数值示例表明,扩展各向异性线性近似表征保持了对各向异性参数的线性关系,它是弱各向异性近似表征的有效扩展,而弱各向异性近似表征是扩展各向异性线性近似表征的特例。通过调节参考点取值,即使各向异性参数较大时,扩展各向异性线性近似表征也能与精确表征吻合较好,具有较高精度。所以扩展各向异性线性近似不仅适用于各向异性参数较小的情况,而且也适用于各向异性参数较大的情况。