正弦加速度激励下石英加速度计的标定方法
2022-01-15孙英博任顺清王常虹
孙英博,任顺清,王常虹
(哈尔滨工业大学空间控制与惯性技术研究中心,哈尔滨 150001)
石英加速度计作为惯性元器件的核心成员之一,广泛应用于火箭运载与航空航天装备中。石英加速度计精度与其制造精度和标定精度有关。受制造工艺限制,其制造精度已趋于极限[1,2]。因此,通过对石英加速度计误差模型和标定方法深入研究来提高其使用精度十分必要。目前,石英加速度计误差模型的标定试验包括重力场实验[3]和高G试验[4]。重力场试验激励程度小,只能对误差模型的一次项充分激励,而高次项和交叉耦合项需要在高G环境中获得充分激励。目前,高G试验主要在线振动台[5-7]、角振动台、火箭橇[8]和离心机[9-12]等设备上开展。其中,离心机在石英加速度计的标定试验中有着较为广泛的应用。
文献[13]提出了一种在带有反转平台的精密离心机上标定陀螺加速度计的方法,但未考虑离心机误差对运动参数输入的影响。文献[14]建立了石英加速度计的静态误差模型并分析了部分误差系数的产生机理,同时研究了精密离心机各项误差对石英加速度计误差模型系数标定精度的相关性,但对标定精度的影响并未具体分析。针对这个问题,文献[15]进行了具体的分析和研究,设计了十姿态标定方法,但能标定的参数有限,对于误差模型三次系数项不能完成标定。文献[16]通过基于精密离心机的十二姿态标定法实现了对石英加速度计全部高次项系数的标定。然而,在现有的基于精密离心机进行的高G试验中,输入激励均为匀速,未涉及变角速率激励领域的研究。针对这个问题,本文提出了在盘式离心机上采用正弦角速度作为激励信号,通过三种姿态下的试验,并采用最小二乘辨识法完成误差模型的参数辨识。首先对盘式离心机误差、加速度计安装误差等误差源进行分析;其次,分析各项位姿误差、离心机自身位姿误差的传递方法,建立盘式离心机误差传递模型;再次,结合误差传递模型,通过齐次变换准确确定输出激励的运动参数,并根据各项运动参数建立完整的加速度计误差模型。最后,设计三姿态变转速试验法实现对加速度计误差模型系数和盘式离心机误差的辨识并进行误差分析,采用对比实验法分析离心机工具误差对参数辨识结果的影响。
1 盘式离心机误差分析
1.1 盘式离心机结构
盘式离心机结构如图1所示。

图1 盘式离心机结构示意图Fig.1 Schematic diagram of precision centrifuge
其中1表示盘式离心机主轴轴套;2表示盘式离心机主轴轴线;3表示盘式离心机台面;4表示石英加速度计的工装夹具;5表示加速度计的安装位置。控制盘式离心机主轴以正弦角速率旋转,在旋转中既能产生余弦周期性的向心加速度,又能产生余弦周期性的切向加速度,且向心加速度的频率是切向加速度频率的2倍。石英加速度计固定在离心机工作平台工装内,其敏感轴与盘式离心机台面轴系对应轴重合。
1.2 盘式离心机位姿误差
对盘式离心机结构分析确定盘式离心机误差源,分析各项误差源产生机理及所在坐标系,建立相应坐标系如图2所示。依据各坐标系位姿关系进行误差传递,得到盘式离心机位姿误差对运动参数的影响。坐标系建立如下:

图2 盘式离心机坐标系示意图Fig.2 Coordinate systems of precision centrifuge
(1)地理坐标系ox1y1z1
地理坐标系为东北天坐标系,其中o1z与当地重力加速方向平行,o1x指向水平东向,o1y指向水平北向,当地纬度为φ。
(2)主轴轴套坐标系ox2y2z2
设主轴轴线产生二维铅垂度误差 Δθx1和Δθy1,因此ox2y2z2相对于ox1y1z1的位姿矩阵为:
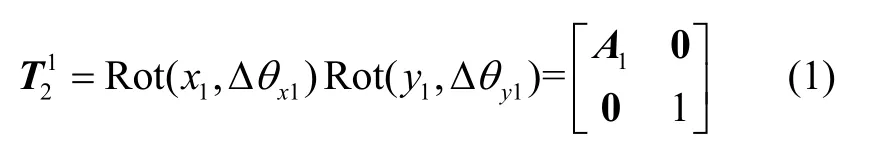
(3)主轴坐标系ox3y3z3
主轴坐标系为变速离心机主轴以角速度ω(t)=4πsin(2πft)rad/s旋转产生的坐标系,在旋转过程中会引入动态误差,包括主轴径向回转误差Δx2(α)、Δy2(α),主轴轴向窜动误差Δz2(α),主轴倾角回转误差 Δθx2(α)、Δθy2(α)以及正弦角速度信号的输入误差Δω。因此ox3y3z3相对于ox2y2z2的位姿矩阵为:

输入正弦角速度信号误差ωΔ 包括常值误差、其它谐波成分干扰误差以及随机干扰误差等对加速度误差产生影响。可以表示为:
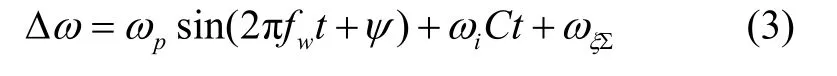
式中,ωp表示角速度周期性变化的幅值,fw为角速度率周期性变化的频率,φ为采样起时刻的相位角;ωiCt表示常值漂移误差;ωξΣ表示随机误差,主要包括转速重复性、转速的对称性、速率波动等。
本文所采用的盘式离心机经试验测得角速度误差幅值为 Δω= 5× 1 0-5rad/s ,当输入正弦角速度信号为ω(t) = 4πsin2πtrad/s时,其角速率最大值为ω= 4πrad/s,此时由正弦角速度信号输入误差产生的作用在加速度计向心加速度输入方向的误差为Δan= 6.4×1 0-5g,类似的,正弦角速度信号输入误差产生的作用在切向加速度方向的误差为Δaτ= 1.5× 1 0-6g。向心加速度和切向加速度会根据加速度计的姿态不同而作用于不同的轴。本文在仿真校验中,对于向心加速度和切向加速度分别引入与Δan和Δaτ幅值相同的白噪声作为系统误差,增强仿真校验的完整性。
(4)工装坐标系
通过工装夹具4的设计,形成加速度计检测质量中心与主轴轴线的距离R。在离心机旋转工作中,由于形变和温度会产生动态半径误差Rd,试验中常进行实时监测。工作台面坐标系相对于主轴坐标系具有垂直度误差Δθx3、Δθy3。因此ox4y4z4相对于ox3y3z3的位姿矩阵为:

(5)加速度计测试坐标系
试验中,加速度计固定在工装夹具上,对于加速度计,安装质心相对工作台面坐标系原点在o4z4方向距离为h1,偏心误差为Δx4和Δy4。安装过程中会引入安装姿态误差Δθx4、Δθy4及Δθz4。因此ox5y5z5相对于ox4y4z4的位姿矩阵为:

式中,Ai表示各坐标系间的相对姿态矩阵;Di表示各坐标系间的相对位移矢量。
2 盘式离心机输出运动参数
假设加速度计的输入轴指向主轴轴线,相当于绕
(4)科氏加速度在加速度计三轴上的分量计的输入基准轴上的比力为当变速z5轴旋转180°,坐标系旋转矩阵为A6,此时加速度离心机主轴以变角速率ω(t)=4πsin(2πft)rad/s旋转标定加速度计时,加速度计的比力输入有4个来源,分别是重力加速度比力、切向加速度、向心加速度和科氏加速度。加速度计所受比力如式(6)所示。

式中:Ag、An、Aτ、Ak分别表示重力加速度比力、向心加速度、切向加速度和科氏加速度在被测加速度计的输入。
(1)重力加速度产生比力在加速度计三轴上的分量
重力加速度产生比力在地理坐标系ox1y1z1中表示为[ 0 0g]T,根据位姿矩阵传递关系可得重力加速度在加速度计坐标系表示:
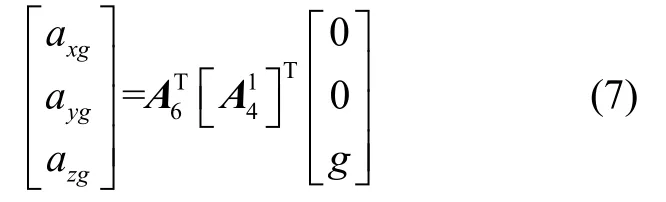
(2)向心加速度在加速度计三轴上的分量
根据位姿误差传递关系,从主轴坐标系到加速度计坐标系的位姿传递矩阵为:
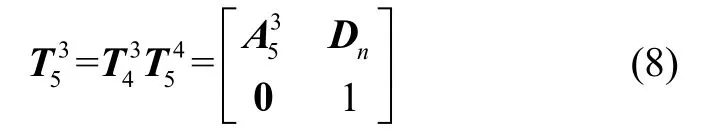
其中,Dn=A3D3+D2为主轴坐标系到加速度计坐标系的位置传递矩阵。向心加速度在三轴上的分量如式(9)可求。

(3)切向加速度在加速度计三轴上的分量
被测加速度计在变角速度激励下会产生与向心加速度方向垂直的切向加速度,更真实地模拟工作环境。Dn表示惯性仪表坐标系到主轴的位置关系,切向加速度位姿矩阵传递关系与向心加速度类似,忽略二阶小量可得,切向加速度在惯性仪表测试坐标系表示为:

科氏加速度只与旋转轴系姿态矩阵有关,因此计算可得切向加速度在惯性仪表测试坐标系表示为:

将式(7)-(11)代入式(6)中可得变速离心机对被测加速度计的精确三轴输入激励分别为:
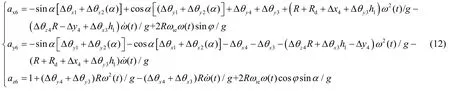
3 石英加速度计误差模型建立
石英加速度计的误差模型为:
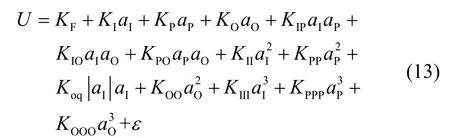
式中:KF为零位偏置,KI为标度因数,KO、KP为交叉轴敏感度,在重力场中可用精密分度头标定;KIO、KPO、KPI为交叉耦合系数;KII、KPP、KOO为输入轴、摆轴、输出轴的二阶非线性系数;Koq为奇异二次项系数;KIII、KPPP、KOOO为三阶非线性系数;ε为随机误差。
在对各项系数标定过程中,由于加速度计主要敏感输入轴方向的比力,因此对输入轴方向的比力输入保留至一阶小量,对摆轴和输出轴方向的比力输入只取标称值,对于各轴交叉耦合以及高阶项系数比力输入构成只取标称值。将各轴输入参数代入误差模型并化简可得:

4 加速度计误差模型标定方法
本文通过设计三姿态试验法实现加速度计误差模型系数和盘式离心机工具误差的辨识。盘式离心机的激励信号设定为ω(t) = 4πsin2πftrad/s,故可得向心加速度为ω2(t)R= 8Rπ2(1- cos4πft)rad/s2,切向加速度为t)= 8Rπ2fcos2πftrad/s2。加速度计三种安装姿态如图3所示。
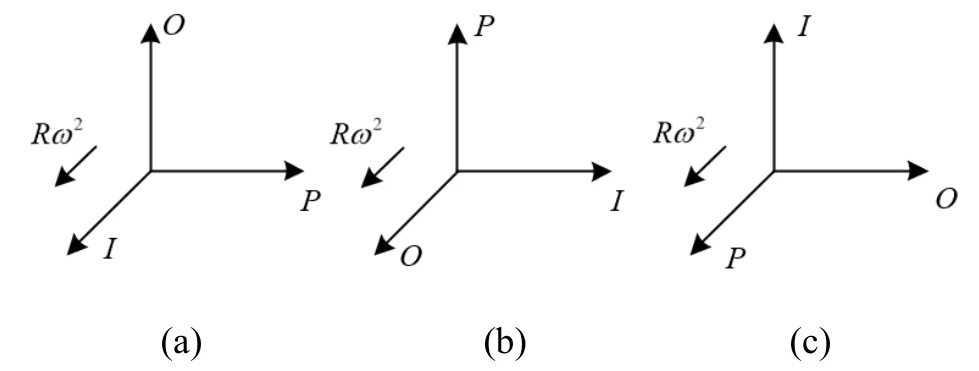
图3 加速度计安装方式Fig. 3 Installation attitudes of accelerometer
4.1 姿态一
加速度计第一种安装姿态如图3(a)所示,输入轴方向始终指向主轴,摆轴指向离心机半径切向,输出轴平行于主轴轴线。由于每次改变安装姿态后安装姿态误差和偏心误差会发生改变,因此将三种安装姿态下的姿态误差记为 Δθx4(i)、 Δθy4(i)、 Δθz4(i),将偏心误差记为 Δx4(i)、Δy4(i),根据正弦函数的整周积分为零,将式(12)化简后可得加速度计各轴输入激励参数:

将式(15)代入式(13)中,其中,本文采用的盘式离心机的半径为1 m,角速度激励信号频率为1 Hz。因此可得加速度计输出表达式如式(16)所示。

式中A表示ω(t)2/g,B表示 -8π2cos4πt/g,C表 示ω(t) /g,D表 示 8π2cos2πt/g,E表 示64π4cos4πtcos2πt/g2。试验中采样频率为50 Hz,采用等时间间隔采样,取 1000个采样点ti(i= 1,2… 1 000);根据式(16),将所有采样点的输出综合表示成矩阵形式,如式(17)所示。

对于式(17),可简写为:

其中,Φ1为满秩阵,故利用最小二乘法可求解误差模型系数矩阵:
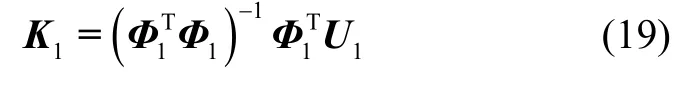
4.2 姿态二
加速度计第二种安装姿态如图3(b)所示,摆轴平行于主轴轴线,输出轴始终指向离心机主轴,输入轴指向离心机半径切向。加速度计各轴输入化简后可得:

将式(20)代入(13)中,加速度计输出表达式为:
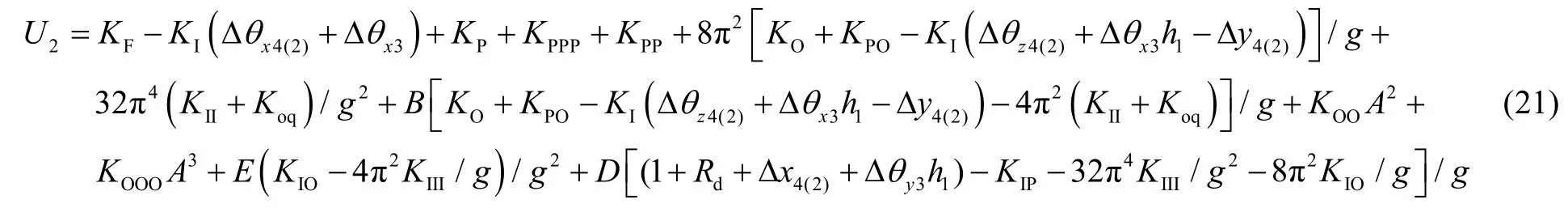
与式(17)类似的,式(21)可写成:

利用最小二乘法可求解误差模型系数矩阵:

4.3 姿态三
加速度计第三种安装姿态如图3(c)所示,摆轴方向始终指向主轴,输出轴始终指向离心机半径切向,输入轴平行于主轴轴线。将式(12)化简后可得加速度计各轴输入:

将式(24)带入式(13)中并整理可得加速度计输出表达式为:

与式(17)类似的,式(25)可简化表示为:

利用最小二乘法可求解误差模型系数矩阵:


表1 加速度计误差模型系数辨识表达式Tab.1 Identification expressions of accelerometer’s error model coefficients
其中,Z1表示 4π2(KII+Koq)/g,Z2表示8π2KPO/g+32π4KOOO/g2。从表1可以看出,三姿态标定方法可以实现对加速度计误差模型二阶、三阶误差项进行全部辨识,同时,盘式离心机部分工具误差也可以实现辨识,为后续对比试验的进行提供了基础。
5 仿真校验与误差分析
5.1 补偿工具误差前的参数辨识结果
对于石英加速度计,根据现有加速度计条件,考虑误差模型参数设置如表2所示。本文采用的盘式离心机的半径为1 m,正弦信号频率为1 Hz,采样频率为50 Hz。因此盘式离心机激励信号角速度为ω(t) = 4πsin2πtrad/s ,向心加速度为ω2(t)R= 8π2(1 - cos4πt)rad/s2,切向加速度为(t) = 8π2cos2πtrad/s2。考虑到输入正弦角速度误差Δω对加速度计输入信号Δaτ、Δan的影响,将系统噪声考虑在内,离心机角速度、向心加速度、切向加速度以及带有系统噪声的加速度计输出如图4所示。

表2 石英加速度计误差模型系数设定值Tab.2 Values of accelerometer’s error model coefficients

图4 加速度计各轴输入激励信号Fig.4 Input excitation signals for each axis of accelerometer
根据先验条件,我们设定误差模型的参数设定值如表2所示,将各轴输入参数和误差模型系数代入误差模型中并混入系统噪声可得加速度计的输出,对加速度计的输出采样,根据前文所述辨识方法可得辨识结果如表3,从表2和表3可以看出误差模型参数辨识结果与设定值的差距相对于设定值在6%之内。

表3 石英加速度计误差模型系数辨识结果Tab.3 Identification results of accelerometer’s error model coefficients
5.2 误差模型参数辨识的不确定度分析
假设实验室纬度为φ= 45.75°,g= 9.8066m/s2,ωie= 7.292 ×1 0-5rad/s 。石英摆式加速度计的指示输出值的不确定度独立且相等,为σU=10-5,由表1可知各系数表达式,以KIII为例可求解误差模型中各系数不确定度。KIII的不确定度表达式为:

类似的,其他系数的不确定度计算如式(29)所示。忽略复杂的计算过程,可得各系数不确定度如表4所示,对比表2和表4的数据可以看出,加速度计误差模型三阶项系数的辨识不确定度大小相对于系数本身均在0.1%以内,二阶项系数辨识不确定度大小相对于系数本身在5.6%以内,部分二阶项系数在1%以内,因此辨识结果满足置信度需求。

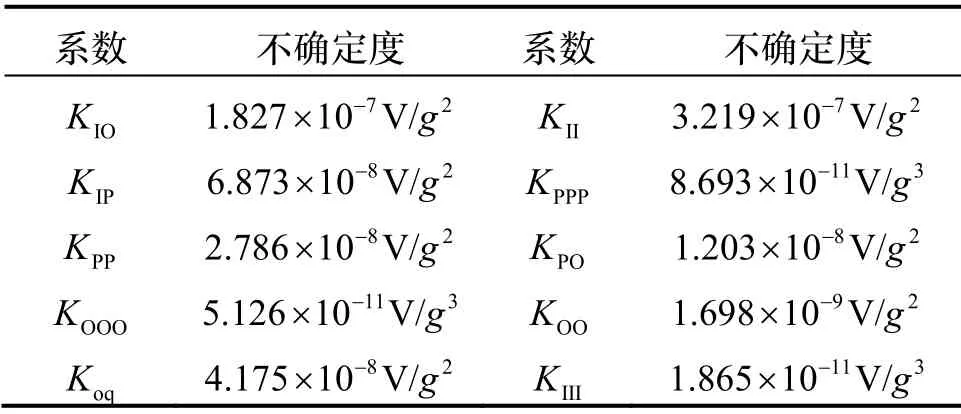
表4 加速度计误差模型系数的不确定度Tab.4 Uncertainties of accelerometer’s error model coefficients
5.3 补偿工具误差前后参数辨识结果对比
从表1可得,盘式离心机误差可以通过最小二乘法进行辨识,因此设计对比试验,将三个姿态下的石英加速度计输出中含有盘式离心机的工具误差的分量进行补偿,并将补偿前的输出记为Ui(i=1,2,3),将补偿后的输出记为类似的,采用相同的辨识方法,将补偿仪表误差后各参数辨识结果记为同时,将补偿仪表误差前后的参数辨识结果差值记为ΔKi,以KOOO为例,补偿前后的辨识误差如式(30)所示。

类似的,忽略复杂的计算过程,误差模型中的其他参数在补偿仪表误差前后的辨识值之差如表5和图5所示。

表5 工具误差对加速度计误差模型参数标定的影响Tab.5 The Influence of instrument errors on the calibration of accelerometer’s error model coefficients
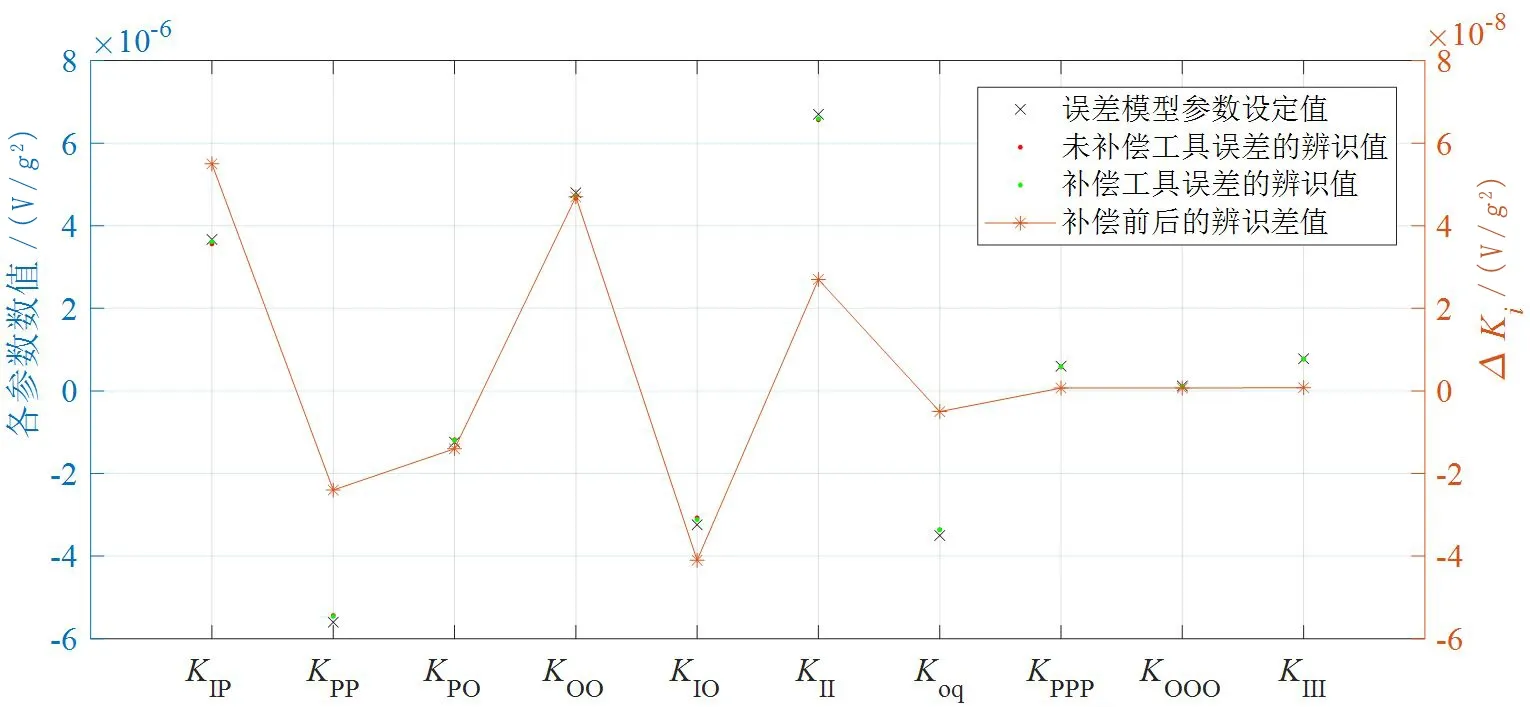
图5 补偿工具误差前后的参数辨识结果Fig.5 Identification results of error model coefficients before and after compensating instrument errors
通过对比试验可以确定输出信号中与离心机工具误差相关的激励分量对误差模型系数标定精度的影响,如表6所示,标定结果的精度为辨识值与设定值的差值占设定值的百分比。可以看出,离心机工具误差的补偿对高阶项系数的标定精度的提升有一定的影响,对于交叉耦合项的影响相对更大一些。因此,在加速度计标定试验中对离心机工具误差的补偿很有必要。

表6 加速度计误差模型系数标定精度Tab.6 Calibration accuracy of the accelerometer’s error model coefficients
根据上述误差分析,相对于传统的误差模型辨识方法,本文采用的正弦角速度输入信号为动态信号,可以同时产生动态的向心加速度和切向加速度,可以更趋近加速度计的高过载工作状态,更充分地激励交叉耦合项等高阶项。本文在误差模型方面首先引入了离心机的仪表误差,提高了误差模型的完整性和置信度;其次,在对比试验中通过先辨识后补偿的方法在一定程度上提高了误差模型系数辨识的精度,与此同时,安装姿态的减少大幅地提升了误差模型的标定效率。
6 结 论
本文通过位姿矩阵传递分析了盘式离心机的仪表误差对加速度计的输入运动参数的影响,并根据所得的运动参数建立了相较传统方法更为完善的加速度计的误差参数标定模型。
本文采用了正弦形式角速度作为盘式离心机的输入信号,在角速度动态变化的同时,引入了动态变化的向心加速度和切向加速度,相较于传统标定方法,在激励信号方面更趋近于加速度计在实际工作环境中的动态过载特性。在标定方法上,通过三种不同姿态的试验可实现误差模型中部分二阶和高阶项系数的独立辨识,避免了离心机各项误差对参数辨识精度的影响,相较于传统方法满足标定精度的同时大幅减少加速度计姿态的改变次数,明显提升了标定效率。
本文通过仿真验证了二阶、三阶系数辨识精度,分析了各项误差系数辨识的不确定度,并通过设计对比实验确定了在补偿动态离心机工具误差前后对各系数辨识结果的影响。
本文所提出的方法可应用于石英加速度计的快速标定,为加速度计的动态实验设计提供参考。
