基于驱动振型进动的半球谐振陀螺旋转调制方法

陈 刚，唐明浩，张海峰，杨松普，贾晨凯

（天津航海仪器研究所，天津 300131）

半球谐振陀螺是一种基于哥氏效应敏感外界角速度的振动陀螺仪。相比传统机械陀螺，它结构简单，核心工作部件只有石英谐振子和电极基座，并且依靠微幅振动工作，无机械磨损，使其具有造价低、可靠性高、寿命长的特点。与光学陀螺相比，它具有更佳的成本、尺寸、质量和功耗比(C-SWaP)[1]。

半球谐振陀螺有力反馈和全角两种工作模式。在力反馈模式中，振型被控制在振型角0°位置，力反馈控制力与哥氏力成正比，据此可以计算出陀螺敏感的角速度，此模式陀螺为速率陀螺。由于抑制哥氏力进动的静电力施力效率不高，可平衡的哥氏力范围有限，因此陀螺测量动态范围小。在全角模式中，振型在谐振子周向自由进动，因为振型进动的角速度与外部输入角速度相差布莱恩系数，可以通过检测振型的进动角增量计算陀螺敏感的角速度，此模式陀螺为速率积分陀螺。全角模式的高带宽、大量程，以及稳定的标度因数使其能够工作在高动态的环境中，但是其允许谐振子自由进动的特性，也带来了陀螺漂移随振型位置变化的弊端，因此以主动驱动振型旋转的方式调制掉漂移从而提高系统等效精度很有必要。

法国赛峰电子与防务公司是目前世界上最成功的半球谐振陀螺制造商之一，它在20世纪90年代开始研制半球谐振陀螺，指出能够通过驱动振型进动一周来调制漂移，这项技术是赛峰公司全角半球谐振陀螺成功的一项关键技术[2-5]。国内外也有一些学者对半球谐振陀螺调制漂移这项技术进行研究，文献[6]提出了振型自进动技术，通过控制驱动力驱使振型进动，减小阻尼不均漂移在陀螺输出中的占比；文献[7]提出了虚拟旋转技术，分析了施加不同大小虚拟旋转速度时对陀螺输出的影响。

上述文献缺乏对振型驱动机理的分析。本文从半球谐振陀螺理想运动方程出发，推导了陀螺在理想和非理想情况下的椭圆参数控制方程，详细说明了陀螺驱动振型进动的机理，根据半球谐振陀螺的漂移特性，提出了一种主动驱动振型进动的半球谐振陀螺旋转调制方法。比较陀螺工作在全角模式和旋转调制模式下的陀螺漂移Allan方差，并从惯导系统的角度出发，通过半实物仿真对旋转调制的效果进行验证。

1 谐振陀螺理想运动方程

半球谐振陀螺二阶振动模态的运动方程是一个二阶线性微分方程组[8]，如式(1)(2)。方程组的两个方程分别描述了激励模态和检测模态，两个模态通过外部输入角速度Ω耦合。由相似系统理论可知，谐振子的运动方程可以等效为二维弹簧-质点模型，如图1。

图1 二维弹簧-质点模型Fig.1 Two-dimensional spring-mass model

将等式两边都除模态质量m：

并且方程有解：

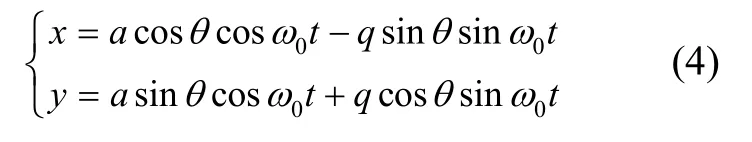
其中，0ω为谐振子固有频率，k为谐振子刚度，α为布莱恩系数，x，y分别为相互正交的检测轴X，Y处的位移，a为振动波腹点的振幅，q为振动波节点的振幅，θ为振型角，fx，fy为谐振子受到的控制力。

可以将二维弹簧-质点模型表达为向量形式：

方程的解为：

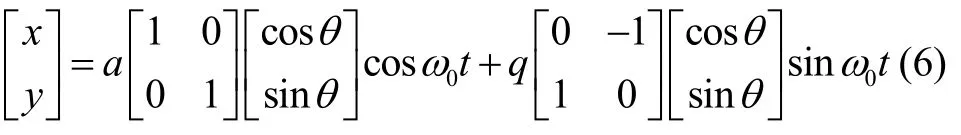
令：

将上述定义带入方程（5）（6）进行整理：

或：

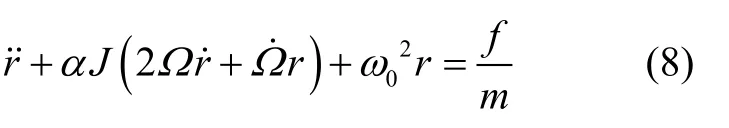
方程的解为：

由此得到向量形式的陀螺等效二维弹簧-质点运动方程，这为推导陀螺振型进动驱动控制方程提供了基础。

2 谐振陀螺振型进动驱动控制方程

在等效的二维弹簧-质点模型中，质点的运动轨迹为一个椭圆，a表示椭圆的长轴，对应振动波腹点的振幅；q表示椭圆的短轴，对应振动波节点的振幅；θ为椭圆长轴相对于电极坐标系的夹角，对应振型角；ω为质点运动的频率，对应振动的频率。称这四个变量为椭圆参数；a、q、θ可以通过全角模式下检测并计算得出，ω等于激励力的频率。

假设激励力的频率不等于固有频率：

则式(9)变为：

为了得到用椭圆参数为变量的方程，需要消去r。忽略a˙˙和q˙˙，用正交的振动相位和空间位置划分各项：

其中φ= (ω0+δω)t。

将式(11)-(14)带入式(8)，并忽略小量可得：

由式(15)可得椭圆参数相关量对应着振动不同的位置和相位，当施加对应的控制力，就可以分别对椭圆参数进行控制。将控制力构造为：

一般使用稳幅回路控制波幅点的振幅，将a控制为常值；由于q会引起椭圆参数控制力的交叉耦合，所以一般使用正交回路抑制波节点振幅，将其控制为0；频率追踪回路使谐振子始终振动在固有频率。在这些条件的基础上，令：

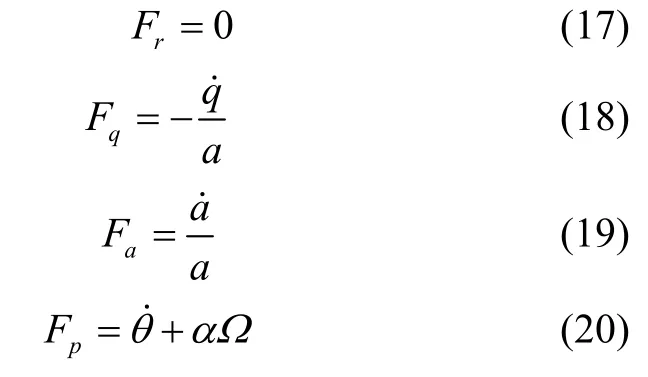
式(17)-(20)展现了陀螺中控制力对于椭圆参数的控制关系。称aF为振幅控制力，Fq为正交控制力，Fp为进动控制力；将式(20)称为谐振陀螺振型进动驱动控制方程，通过施加进动控制力，可以主动地驱动振型旋转，这是半球谐振陀螺旋转调制的基础。

3 控制方程误差分析

在实际的谐振陀螺中，谐振子存在周向阻尼不均和因周向质量不均引起的频率裂解。谐振子分布在一周的阻尼不均匀，等效的作用效果是谐振子存在一个最大阻尼轴和与其正交的最小阻尼轴。在谐振子周向质量不均分布函数中，对陀螺性能影响最大的是其中四次谐波引起的频率裂解[9]，谐振子在自由振动状态下会出现两个相互正交的频率轴，谐振子振动波腹处在这两个轴时分别达到最大固有频率和最小固有频率。频率裂解会使波节点振幅快速增长。为了减小陀螺在力反馈模式下的漂移，一般会通过修调的方式将刚度轴对准电极轴，而阻尼轴和电极轴的夹角则不可控。

根据Lynch推导的谐振子不理想条件下存在质量不均、阻尼不均等的谐振陀螺运动方程[8]，将其写成向量形式并忽略了输入角速度的平方项，因为此项对频率的影响忽略不计：

其中:

ω1、ω2、τ1、τ2分别对应着振型在0 °时两个模态的固有频率和衰减时间。θτ、θω分别表示最大阻尼轴和最大刚度轴相对于电极坐标系X轴的偏角。可以将式(21)写为：

同样地，将式(12)-(14)带入式(23)，将各项以正交的空间位置和正交的相位划分，并合并同类项。设ra为波幅点方向的单位向量，rq为波节点方向的单位向量。假设开启了正交回路、稳幅回路、频率追踪回路三条回路的控制。可以用向量求模的方式提取出空间方向上的量。用左乘式（23）可得：

用rqT左乘式(23)可得：

式(24)-(27)说明了谐振子在非理想情况下各个控制力和椭圆参数以及相关误差的关系。振动波幅点的振幅会因为阻尼而衰减，控制力Fa的作用是补充因阻尼损失的能量；控制力Fq抑制谐振子的频率裂解而导致波节点的振幅随时间增长。从非理想情况下谐振陀螺振型进动驱动控制方程(27)中可得，谐振子的阻尼周向不均会导致陀螺存在和振型角相关的周期性漂移误差。

4 谐振陀螺漂移旋转调制方法

不同于光学陀螺惯导的旋转调制技术，半球谐振陀螺惯导无需旋转框架，系统中的每一只陀螺在正常全角模式敏感外部角速度的同时，都处于主动驱动振型绕陀螺自身敏感轴进动旋转状态，从而实现漂移的调制，这也使得半球谐振惯导能以纯捷联的方式得到旋转调制的效果。

谐振子的周向阻尼不均会引起陀螺漂移误差ε，且该漂移误差和振型角相关：

当陀螺工作在全角模式时，振型会自由进动到任意角度，这会导致陀螺漂移持续发生变化，降低陀螺输出的稳定性。陀螺振型因漂移产生进动，这种情况下的陀螺漂移会表现以趋势项为主的斜漂，使惯导解算产生更大的误差。阻尼不均漂移误差具有在振型角度[θ0，θ0+π]整周期均值为0的特性：

根据此特性，可以施加控制力Fp驱动振型进动一周，从而达到消除漂移误差的效果。对于惯导解算定位误差来说，陀螺漂移的影响会随时间积累，所以其关注在时间轴上对陀螺漂移的积分结果。对于不确定的阻尼轴θτ，当振型角θ和时间成线性关系，即振型匀速进动时，在时间轴上对陀螺漂移的整周期积分有最好的效果，假设θ=vt，v为振型进动的速度：

图2展示了半球谐振陀螺旋转调制模式的实现方法。检测电极a、q检测到的振动信号，分别由参考信号 cosω0t和 sinω0t解调并低通滤波，得到Cx、Sx、Cy、Sy四个直流信号量，参考信号的频率由频率追踪回路提供；四个直流信号量经过全角信号解算后得到四个椭圆参数：a、q、φ、θ。a表示波幅点振幅对应的电压信号，q表示波节点振幅对应的电压信号，φ表示参考信号和振动信号的相位差，θ表示振型角。a、q、φ分别为稳幅回路、正交回路和频率追踪回路的控制量。振型角θ信号量输入到旋转调制控制回路后，经PID控制，输出进动控制力Fp对应的控制电压，分配到A、Q激励电极上，使得控制力作用在振型波节点上，驱动振型进动。陀螺漂移随振型进动的变化如图3所示。

图2 半球谐振陀螺旋转调制模式原理框图Fig.2 The principle block diagram of HRG rotation modulation mode

图3 半球谐振陀螺漂移随振型进动变化Fig.3 The drift of HRG changes with the procession of the vibration mode

5 实验与半实物仿真定位试验

将半球谐振陀螺静置在测试平板上。在室温变化条件下，待陀螺稳定后分别录取常规全角模式和旋转调制模式下的陀螺长时间输出数据。图4展示了两种工作模式下陀螺输出的Allan方差，其中虚线代表常规全角模式，实线代表旋转调制模式，tΔ表示数据处理间隔时间。旋转调制模式下陀螺输出的零偏不稳定性较常规全角模式降低了一个数量级以上，更长的探底时间说明旋转调制模式在长时间会有更佳的性能。从图4中也能明显看出旋转调制模式对角随机游走和速率斜坡也有明显的抑制。

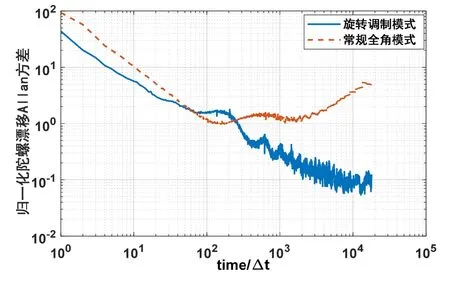
图4 常规全角模式和旋转调制模式陀螺漂移Allan方差对比Fig.4 Comparison of Allan variance of gyro bias between conventional whole angle mode and rotation modulation mode

同样在室温变化条件下，将半球谐振陀螺设置为常规全角模式和旋转调制模式，录取半球谐振陀螺惯导系统原始脉冲数据，进行半实物惯导解算仿真，选取的全角模式和旋转调制模式的数据在同一谐振频率变化趋势和范围，保证受温度的影响相同。结果如图5所示。以系统工作在全角模式下最大的定位误差为基准，旋转调制模式下的定位误差减小了50%。

图5 常规全角模式和旋转调制模式惯导半实物仿真定位误差对比Fig.5 Comparison of semi-physical inertial navigation simulation positioning error between conventional whole angle mode and rotation modulation mode

6 结 论

本文从半球谐振陀螺等效的二维弹簧质点运动模型出发，分别推导了半球谐振陀螺在理想情况下和非理想情况下工作在全角模式的椭圆参数控制方程，从机理上阐述了半球谐振陀螺驱动振型进动的方法，说明了通过振型进动旋转调制陀螺漂移的可行性。在实验中，比较了全角模式和旋转调制模式下的陀螺漂移Allan方差以及惯导的半实物仿真结果，旋转调制模式下的陀螺零偏稳定性（Allan方差）相比常规全角模式下提高了一个数量级以上，惯导系统的定位精度（最大值）提高50%。本文在分析半球谐振陀螺的漂移特性时，只考虑了陀螺谐振子本体的误差，较为理想。在实际的情况中还可能存在陀螺检测电极与激励电极增益不一致等误差，也会对陀螺漂移产生影响[10]，更全面的陀螺漂移特性分析下的旋转调制方法有待后续研究。