基于WNN的全弹性空间机器人自适应非奇异快速终端滑模控制算法

付晓东，陈 力

（福州大学 机械工程及自动化学院，福州 350108）

空间机器人在维修或捕获故障卫星，为航天器补给物资等方面发挥着不可替代的作用，大型空间部件（如太阳能电池，无线电天线）的安装，空间站建造等都离不开空间机器人，因此，其动力学模拟及运动控制技术受科研工作者广泛关注[1-7]。空间机器人在地面环境中加工、组装、调试，机械加工装配误差只能减弱，难以消除，而且一旦进入极端恶劣的太空环境，易受宇宙射线等的冲击，这些建模误差及外部干扰易导致控制性能减弱，甚至失控的发生。滑模控制是处理具有参数摄动、外部扰动等非线性因素的有效方法，具有强鲁棒、易工程化等优点[8]，但存在有限时间收敛、抖振现象和奇异性等问题。为解决这些问题，研究人员提出了终端滑模控制[9]、快速终端滑模控制[10]、非奇异终端滑模控制[11]，解决了传统滑模控制的部分缺点。文献[12]设计了鲁棒非奇异快速终端滑模控制器，收敛速度快，且避免了奇异性，但在总控制器中引入H∞项补偿系统不确定性和外部干扰，H∞项的引入导致控制器运算量大，不易于航天实现。文献[13]提出了自校正模糊PID非奇异快速终端滑模控制，有快速响应、稳态误差小等优点，但是采用计算量大的TDE算法来估计未知动力学模型，而且所采用的PID控制增益影响系统稳定性。针对上述问题，本文设计了基于小波神经网络（Wavelet neural network, WNN）的自适应非奇异快速终端滑模控制算法，利用WNN网络估计系统中的不确定项上界，构造的非奇异滑模面保证滑模控制的非奇异性，采用自适应算法自动调整控制器参数，并且设计补偿项，减少抖振，确保高精度跟踪。

值得指出的是，空间机器人发射、运行、维护成本很高，空间探测任务复杂、条件严苛，于是通常按照轻质、承载力大、工作范围广的要求设计。空间机器人主要由基座、臂构成，基座上固定有平行导轨，臂在导轨上移动工作。臂由若干杆铰接而成，通常具有细长、结构刚度偏低的特性，由安装于铰接处的谐波驱动柔轮驱动，而这种驱动器使电机转子转角与关节转角不同步，相当于在两者之间设置了力矩滤波器，引入了关节柔性。当空间机器人受到外部太空激励或执行抓捕及后续一体化操作任务时，极易诱发导轨、关节、杆的弹性振动，从而影响运动稳定性。因此，为实现空间机器人的高精度、高稳定性控制，建模时考虑基座、关节、臂的弹性特征很有必要，但是全弹性空间机器人运动、振动控制势必会增大建模、分解及控制器设计的难度。目前，针对弹性系统的研究已经深入[14]，文献[15]提出了柔性关节空间机器人动力学模型，并设计了基于观测器的鲁棒控制，但是并未考虑基座、臂杆柔性振动对系统的影响。文献[16]提出了弹性基座、柔性关节空间机器人动力学模型，并设计了高精度运动控制算法，但是在建模分析及算法设计时均忽略了臂杆柔性。文献[17]提出了柔性关节、柔性臂空间机器人动力学模型，但是将模型分解为慢变子系统与双快变子系统，因此，导致运动及振动控制器设计繁杂。文献[18]提出了弹性基座、柔性臂空间机器人运动控制及抑振方案，但是在模型设计时，未考虑关节柔性振动的影响，而且设计了基于混合轨迹的终端滑模算法，无法保证系统快速收敛。上述研究主要考虑基座、关节、臂部分构件弹性的影响，而全弹性空间机器人的研究比较少见。

鉴于空天高精度控制对多重弹性振动抑制的必要要求以及空间机器人建模误差及外部干扰的普遍存在性，本文针对基座、关节、臂全弹性空间机器人系统，设计了基于WNN结构、混合轨迹法、减振线性二次最优法的自适应非奇异快速终端滑模复合控制算法。根据奇异摄动理论将全弹性系统分解为包含基座、关节弹性振动的快变子系统，包含基座、关节刚性运动及杆弹性振动的慢变子系统。减振线性二次最优法抑制快变子系统多重弹性振动，自适应非奇异快速终端滑模控制实现系统刚性运动的高精度追踪，满足对建模误差、外部干扰的不敏感性。混合轨迹法抑制多杆弹性振动，最后仿真校验了算法的可行性。

1 动力学建模及奇异摄动分解

1.1 基座、关节、臂全弹性空间机器人动力学建模

基座、关节、臂全弹性影响下的漂浮基空间机器人结构如图1所示，其中，B0表示基座，Bi(i=1,2)为柔性杆，q0为基座姿态角，qi(i= 1,2)为关节转角，qmi(i= 1,2)为关节电机转子转角。将弹性基座、关节分别等效为线性弹簧、扭转弹簧[19]，qb为基座弹性变量，σi=qmi-qi(i= 1,2)为关节柔性变量。柔性臂视作Euler-Bernoulli简支梁，用假设模态法分析，并保留前两阶模态，vi（t）为t时刻杆Bi任意截面处横向弹性变形。建立惯性坐标系OXY及各分体连体坐标系OjXjYj（j= 0,1,2），其中，O0与载体质心重合，Oi(i= 1,2)在关节铰几何中心，OC为系统总质心。

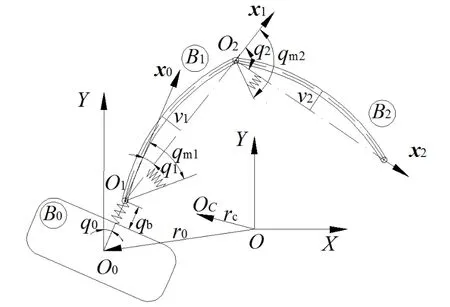
图1 基座、关节、臂全弹性空间机器人Fig.1 Space robot with flexible-base two-flexible-link and two-flexible-joint

不计电机转子质量及重力，考虑外部扰动的影响，根据系统在惯性坐标系中的几何位置关系，结合质心定理，拉格朗日方程得载体位置不控、姿态受控动力学模型：

1.2 模型奇异摄动分解

其中， I ∈R2×2为单位矩阵，Kc∈R2×2为对称正定补偿矩阵，un=unk+uns∈R2×1为待设计的控制器，式中unk为快变子系统控制器，uns为慢变子系统控制器。

根据动力学模型式(1)-(3)，快、慢变子变量，

总控制器式(4)，得包含qb、σ的快变子系统：

包含q、δ的慢变子系统：

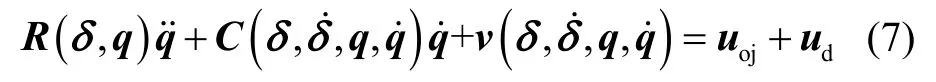
2 控制算法分析

2.1 快变子系统控制器设计

利用线性二次最优算法同时抑制快变子系统式(5)中 bq、σ的振动，构造性能指标函数其中Rk∈R2×2为对称正定矩阵，分别表示qk与unk的性能量度权重，现将快变子系统控制器（线性最优双重弹性减振控制器）设计为：

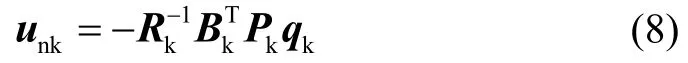
其中，Pk为黎卡提方程的解。

2.2 慢变子系统控制器设计

2.2.1 鲁棒非奇异快速终端滑模控制

定义变量：

其中，x∈Rn为任意矢量，∂≥1为正常数，由式(10)得：

定义位置追踪误差e=q-qd，其中qd表示系统基座姿态、关节期望轨迹矢量。设计非奇异快速终端滑模面为：

式中，k1＞0，k2＞0，1＜β＜2，γ＞β。

滑模面式(12)对时间求导，并根据式(10)(11)得：

设计鲁棒非奇异快速终端滑模控制器（Robust nonsingular fast terminal sliding mode control,RNFTSMC）为：

式中,us=-R0（ρ+δ）sgn(s)为切换控制器，uc=-R0Ks为补偿控制器，补偿系统不确定性引起的扰动。δ与K为任意正常数。

将式(15)代入式(13)得：

定理1：对于慢变刚性子系统式(9)，在设计的RNFTSMC控制律式(15)作用下，可确保系统刚性变量追踪误差e在有限时间内收敛到0。

时间求导，并代入式(16)得：

其中，b1，b2为正常数，具体表达式如下所示：

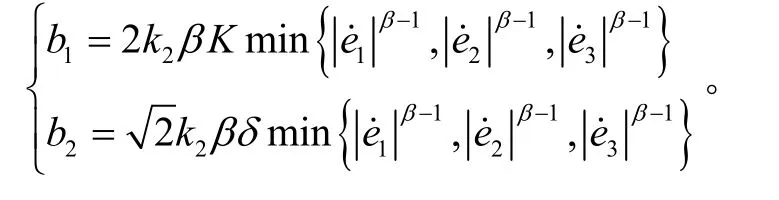
为便于后文计算，式(17)计算得：

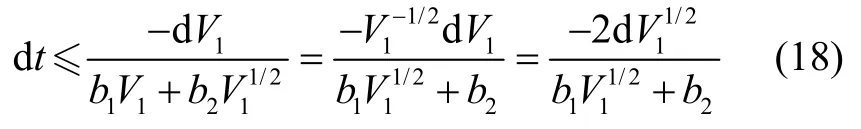
选取系统误差从e≠0到e=0的趋近时间为tr，式(18)在 0～tr上取积分得：

若2b选取足够大，可以确保下式成立：

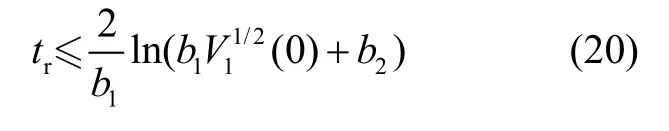
基于上述分析可知，所设计的RNFTSMC，可以确保系统式(9)在有限时间内收敛到0。证毕。

2.2.2 基于WNN的自适应非奇异快速终端滑模控制

NFTSMC的设计是假设总误差Δu的最大上界ρ已知的，实际工作中，ρ值很难估算或求取，而且，为了确保控制器的有效性，当Δu增大，ρ也增大，但是控制器中ρ值一旦确定，无法自行调整，导致抖振甚至控制失效，NFTSMC的局限性比较明显。因此，本节利用神经网络对ρ估计，目前，使用神经网络估计不确定性上限已获得良好性能，考虑到WNN网络结构节点少，逼近未知函数速度快，所以用来逼近ρ值。WNN在隐藏单元中包含有小波函数，结构如图2所示。

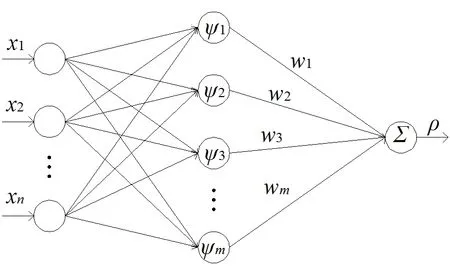
图2 小波神经网络结构图Fig.2 Wavelet neural network structure diagram

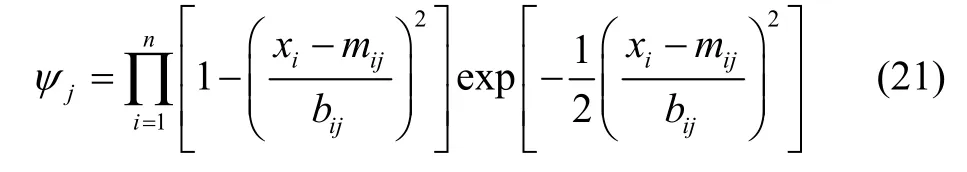
式中，mij为WNN节点伸缩参数，bij为节点平移参数。输出值ρ表达式为ρ=WTΦ，其中。

设计基于WNN的自适应非奇异快速终端滑模控制(Adaptive nonsingular fast terminal sliding mode control based on WNN, ANFTSMC-W)为：

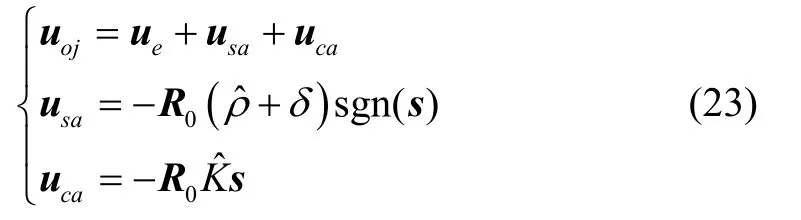
更新律为：

其中，ωW，ωK为任意正常数，将式(23)(24)代入式(13)得：

定理2：对于子系统式(9)，在建模误差与外部扰动完全未知的情况下，ANFTSMC-W控制律式(23)，及更新律式(24)，可确保系统状态渐近收敛于滑模面s=0上。

证明：构造李雅普诺夫函数2V∈R为：

V2对时间求导，并代入式(23)(25)得：

将式(24)代入式(27)得：

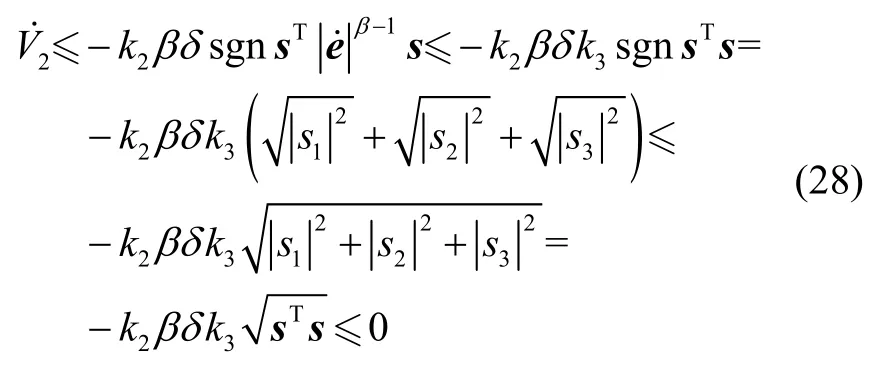
根据李雅普诺夫稳定性理论得，慢变刚性子系统式(9)采用ANFTSMC-W控制律式(23)及更新律式(24)，可确保从初始状态收敛到滑模面s=0上，结合定理1，得系统有限时间稳定，证毕。

2.2.3 改进的WNN非奇异快速终端滑模控制

ANFTSMC-W只能实现慢变子系统基座姿态、关节q的轨迹精确追踪，却不能抑制臂弹性振动。为此使用虚拟力概念，修正原有的期望轨迹，构造混合轨迹qh，设计改进的ANFTSMC-W算法，实现q跟踪及δ的抑振控制。引入虚拟力F∈R3×1，定义eh=qh-qd，生成eh的指令发生器如下所示：

其中，A,B∈R3×3为常正定对角矩阵。

令混合误差er=q-qh，将控制器式(23)及更新律式(24)中qd、e及s分别替换为qh、er及sr，得改进后的ANFTSMC-W为：

更新律为：

将控制器式(30)代入刚性子系统式(7)得：

设计虚拟力F为：

其中，Rs为性能指标函数中F对应的加权矩阵，Ps为对应黎卡提方程的解。当ηs=0或满足条件式(35)时，系统稳定[20]。

3 仿真试验与分析

为了验证本文提出的ANFTSMC-W的有效性，拟对图1所示的存在建模误差及外部扰动的全弹性空间机器人分别进行弹性不控模式与弹性控制模式下的仿真研究。

全弹性空间机器人精确已知的模型参数值为：ρ1= 3.5kg·m ，ρ2= 1.1kg·m ，Jm1=Jm2= 0.1kg· m2，EI1=EI2= 100N/m2，km1=km1= 50Nm/rad ，kb= 500N/m 。对于存在建模误差的参数，以误差值占标称值的20%为指标，即ξ=ξ0+0.2ξ0，其中ξ0为标称值，ξ为真实值。取基座标称质量 (m0)0= 33kg ，标称转动惯量 (J0)0= 25kg· m2，两杆标称杆长(l1)0=(l2)0= 1.25m 。仿真起始，设系统弹性构件（基座、关节、臂）均未变形，O0O1的距离l0= 1.5m ，初始构形取为qb（0 ） = 0m ，q（0 ） =[ 0.7,0.95,1.2]Trad，δ（ 0）=0m ，qm（0 ） =[ 0.95,1.2]Trad ，各构型高阶项的初值全部取为 0，外部干扰选取为ud=[ 0 .5,0.5,0.5]T(N·m)。

取期望轨迹为qd=[ 0.5,1,1.5]Trad 。采用四阶Runge-Kutta方法仿真，步长0.01 s，控制器参数选取为Kc=diag(80,80)，k1=k2= 0.1，γ=2.2，β=1.5，δ=ωW=ωK= 0.1。

3.1 弹性不控模式

关闭基座、关节弹性振动主动控制器unk，不采用抑制臂振动的虚拟力F，运用式(4)(23)(24)构成的算法仿真，结果如图3-5所示，其中，图3表示系统刚性轨迹q的追踪曲线，图4为快变子系统弹性变量qb、σ的振动曲线，图5为慢变子系统弹性杆前两阶模态振动曲线。

图3 轨迹跟踪曲线Fig.3 Trajectory tracking curves

图4 基座、关节弹性振动曲线Fig.4 Elastic vibration curves of base and joints

图5 杆弹性振动曲线Fig.5 Elastic vibration curves of links

由图3可知，基座姿态、关节1，关节2轨迹跟踪振幅分别为0.01rad，0.02rad，0.005rad，收敛时间在2s以内。轨迹跟踪振幅小，收敛时间快，说明所设计的ANFTSMC-W控制律，在系统存在弹性影响的情况下，对系统建模误差及外部干扰具有不敏感性，满足快速收敛条件。由图4-5可知，基座的弹性振幅在0.015m左右，关节2的弹性振幅在0.3rad左右，杆1与杆2的一阶模态振幅均在0.01m左右。由于建模误差及外部扰动等激励作用，关节1及杆1的二阶模态振动明显增加。

3.2 弹性控制模式

开启基座、关节弹性振动主动控制器unk、并引入虚拟力F，运用式(4)(8)(30)(31)(34)构成的算法仿真，结果如图6-8所示，其中，图6为系统刚性轨迹跟踪曲线，图7为qb、σ振动曲线，图8为两杆前两阶模态振动曲线。

图6 轨迹跟踪曲线Fig.6 Trajectory tracking curves

图7 基座、关节弹性振动曲线Fig.7 Elastic vibration curves of base and joints

图8 杆弹性振动曲线Fig.8 Elastic vibration curves of links

由图6-8可知，采用本文的复合控制算法，q的跟踪精度显著提高，关节1、关节2的振动被抑制在±0 .1rad， ± 0.05rad 以内，收敛时间在2s以内，杆1、杆2的一阶模态振动被抑制在±1.8mm以内。基座、关节、臂的振动均得到有效抑制，并且稳定后的振动维持在许可范围内。证实了本文提出基于WNN的自适应非奇异快速终端滑模控制及多重弹性减振控制构成的复合控制算法具有跟踪精度高、响应速度快、避免奇异性(由所设计的非奇异滑模面决定)、对外界干扰和建模不确定性具有较强的鲁棒性，并抑制多重弹性振动的特点。

4 结 论

针对存在参数建模误差及外部干扰的基座、关节、臂全弹性空间机器人系统，提出了一种基于WNN的自适应非奇异快速终端滑模控制算法。采用奇异摄动法分解全弹性空间机器人为慢、快变子系统。然后设计相应的控制算法，用WNN估计系统建模误差与外部干扰的最大上界，用虚拟力抑制臂的振动，所设计的滑模面避免奇异值的产生。仿真结果表明，复合算法对系统建模误差与外部干扰具有鲁棒性，并且自主估计其有限上界，能主动控制系统基座、关节、臂多重弹性振动，且在有限时间内稳定、快速收敛。

由上述结论可知，文中所提出的算法能实现对全弹性空间机器人的运动振动控制，未来将对如何利用全弹性空间机器人实现对非合作航天器的捕获操作开展进一步研究。